Deck 12: GlM 1: Comparing Several Independent Means
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/28
Play
Full screen (f)
Deck 12: GlM 1: Comparing Several Independent Means
1
If the differences between group means are large enough, then:
A)It is likely that the assumption of sphericity will have been violated.
B)The assumption of homogeneity of variances is likely to have been violated.
C)The resulting model will be a better fit of the data than the grand mean.
D)The resulting model will be a poorer fit of the data than the grand mean.
A)It is likely that the assumption of sphericity will have been violated.
B)The assumption of homogeneity of variances is likely to have been violated.
C)The resulting model will be a better fit of the data than the grand mean.
D)The resulting model will be a poorer fit of the data than the grand mean.
C
2
Imagine you compare the effectiveness of four different types of stimulant to keep you awake while revising statistics using a one-way ANOVA. The null hypothesis would be that all four treatments have the same effect on the mean time kept awake. How would you interpret the alternative hypothesis?
A)All four stimulants have different effects on the mean time spent awake.
B)At least two of the stimulants will have different effects on the mean time spent awake.
C)None of the above
D)Two of the four stimulants have the same effect on the mean time spent awake.
A)All four stimulants have different effects on the mean time spent awake.
B)At least two of the stimulants will have different effects on the mean time spent awake.
C)None of the above
D)Two of the four stimulants have the same effect on the mean time spent awake.
B
3
When the between-groups variance is a lot larger than the within-groups variance, the F-value is ____ and the likelihood of such a result occurring because of sampling error is _____
A)small; low
B)large; high
C)large; low
D)small; high
A)small; low
B)large; high
C)large; low
D)small; high
C
4
What is the overall effect of an independent variable on a dependent variable known as?
A)The interaction effect
B)The main effect
C)The direct effect
D)The indirect effect
A)The interaction effect
B)The main effect
C)The direct effect
D)The indirect effect

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
5
The table below contains the length of time (minutes) for which different groups of students were able to stay awake to revise statistics after consuming 500 ml of one of three different types of stimulants. What is the variation in scores from groups A to B to C known as?
A)The within-groups variance
B)Homogeneity of variance
C)The grand variance
D)The between-groups variance
A)The within-groups variance
B)Homogeneity of variance
C)The grand variance
D)The between-groups variance

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
6
A psychologist was looking at the effects of an intervention on depression levels. Three groups were used: waiting list control, treatment and post-treatment (a group who had had the treatment 6 months before).
-The SPSS output is below. Based on this output, what should the researcher report? Test of Homogeneity of Variances
BDIDIF
ANOVA
BDIDIF
Robust Tests of Equality of Means
BDIDIF
a. Asymptotically distributed.
A)The treatment groups did not have a significant effect on depression levels, F(2, 26.44) = 4.35.
B)The treatment groups had a significant effect on depression levels, F(2, 45) = 5.11.
C)The treatment groups did not have a significant effect on the change in depression levels, F(2, 35.10) = 5.11.
D)The treatment groups had a significant effect on the depression levels, F(2, 26.44) = 4.35.
-The SPSS output is below. Based on this output, what should the researcher report? Test of Homogeneity of Variances
BDIDIF
ANOVA
BDIDIF
Robust Tests of Equality of Means
BDIDIF
a. Asymptotically distributed.
A)The treatment groups did not have a significant effect on depression levels, F(2, 26.44) = 4.35.
B)The treatment groups had a significant effect on depression levels, F(2, 45) = 5.11.
C)The treatment groups did not have a significant effect on the change in depression levels, F(2, 35.10) = 5.11.
D)The treatment groups had a significant effect on the depression levels, F(2, 26.44) = 4.35.

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
7
Which of the following is not a rule for conducting orthogonal contrasts?
A)The sum of weights for a comparison should not be zero.
B)The group that is singled out in one comparison should be excluded from any subsequent contrasts.
C)For a given contrast, the weights assigned to the group(s) in one chunk of variation should be equal to the number of groups in the opposite chunk of variation.
D)If we give a group a weight of zero then this eliminates that group from all calculations.
A)The sum of weights for a comparison should not be zero.
B)The group that is singled out in one comparison should be excluded from any subsequent contrasts.
C)For a given contrast, the weights assigned to the group(s) in one chunk of variation should be equal to the number of groups in the opposite chunk of variation.
D)If we give a group a weight of zero then this eliminates that group from all calculations.

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
8
The student welfare office was interested in trying to enhance students' exam performance by investigating the effects of various interventions. They took five groups of students before their statistics exams and gave them one of five interventions: (1) a control group just sat in a room contemplating the task ahead; (2) the second group had a yoga class to relax them; (3) the third group were told they would get monetary rewards contingent upon the grade they received in the exam; (4) the fourth group were given beta-blockers to calm their nerves; and (5) the fifth group were encouraged to sit around winding each other up about how much revision they had/hadn't done (a bit like what usually happens). The final percentage obtained in the exam was the dependent variable. Using the critical values for F, how would you report the result in the table below?
A)Type of intervention had a significant effect on levels of exam performance, F(4, 29) = 12.43, p < .01.
B)Type of intervention did not have a significant effect on levels of exam performance, F(4, 29) = 12.43, p > .05.
C)Type of intervention did not have a significant effect on levels of exam performance, F(4, 33) = 12.43, p > .01.
D)Type of intervention had a significant effect on levels of exam performance, F(4, 33) = 12.43, p < .01.
A)Type of intervention had a significant effect on levels of exam performance, F(4, 29) = 12.43, p < .01.
B)Type of intervention did not have a significant effect on levels of exam performance, F(4, 29) = 12.43, p > .05.
C)Type of intervention did not have a significant effect on levels of exam performance, F(4, 33) = 12.43, p > .01.
D)Type of intervention had a significant effect on levels of exam performance, F(4, 33) = 12.43, p < .01.

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
9
How can we decide whether our group means are significantly different in an ANOVA?
A)By reviewing the standard error.
B)By reviewing the F-statistic.
C)By reviewing the Mean.
D)By reviewing the Z-score.
A)By reviewing the standard error.
B)By reviewing the F-statistic.
C)By reviewing the Mean.
D)By reviewing the Z-score.

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
10
A researcher wanted to see the effects of different learning strategies. A control group simply read the book Discovering Statistics (Book), a second group read the book and completed the 'end of chapter exercises' (Book & Exercises), and a third group read the book, did the end of chapter exercises and also completed the web materials (All Activities). The researcher predicted that the 'all activities' and 'book and exercises' groups would perform better than the book group on a subsequent test, but that the 'book and exercises' group would perform worse than the 'all activities' group. Which coding scheme would test these hypotheses in a set of planned comparisons? (Hint: The sum of weights for a comparison should be zero. If you add up the weights for a given contrast the result should be zero.)
A)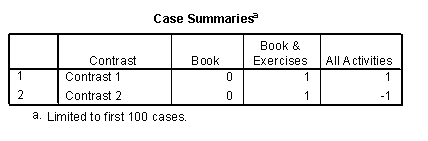
B)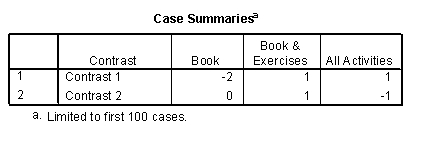
C)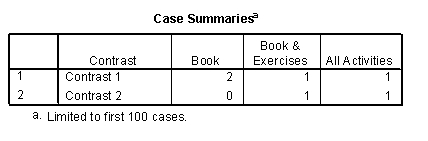
D) Case Summaries
a. Limited to first 100 cases.
A)

B)

C)

D) Case Summaries
a. Limited to first 100 cases.

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
11
What two assumptions must not be violated when running an ANOVA?a. By reviewing the standard error.
A)Homogeneity and normality.
B)Heterogeneity and normality.
C)Homogeneity and non-normality.
D)Heteroscedasticity and normality.
A)Homogeneity and normality.
B)Heterogeneity and normality.
C)Homogeneity and non-normality.
D)Heteroscedasticity and normality.

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
12
Imagine we conduct a one-way independent ANOVA with four levels on our independent variable and obtain a significant result. Given that we had equal sample sizes, we did not make any predictions about which groups would differ before the experiment and we want guaranteed control over the Type I error rate, which would be the best test to investigate which groups differ?
A)Hochberg's GT2
B)Helmert
C)Orthogonal contrasts
D)Bonferroni
A)Hochberg's GT2
B)Helmert
C)Orthogonal contrasts
D)Bonferroni

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
13
After an ANOVA you need more analysis to find out which groups differ. When you did not generate specific hypotheses before the experiment use:
A)t-tests
B)Bootstrapping
C)Post hoc tests
D)Planned contrasts
A)t-tests
B)Bootstrapping
C)Post hoc tests
D)Planned contrasts

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
14
Subsequent to obtaining a significant result from an exploratory one-way independent ANOVA, a researcher decided to conduct three t-tests to investigate where the differences between groups lie. Which of the following statements is correct?
A)The researcher should accept as statistically significant tests with a probability value of less than 0.016 to avoid making a Type I error.
B)The researcher should have conducted orthogonal contrasts instead of t-tests to avoid making a Type I error.
C)This is the correct method to use.The researcher did not make any predictions about which groups will differ before running the experiment, therefore contrasts and post hoc tests cannot be used.
D)None of these options are correct.
A)The researcher should accept as statistically significant tests with a probability value of less than 0.016 to avoid making a Type I error.
B)The researcher should have conducted orthogonal contrasts instead of t-tests to avoid making a Type I error.
C)This is the correct method to use.The researcher did not make any predictions about which groups will differ before running the experiment, therefore contrasts and post hoc tests cannot be used.
D)None of these options are correct.

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
15
A psychologist was looking at the effects of an intervention on depression levels. Three groups were used: waiting list control, treatment and post-treatment (a group who had had the treatment 6 months before).
-Based on the output for these tests, what should the researcher conclude? Test of Homogeneity of Variances
BDIDIF
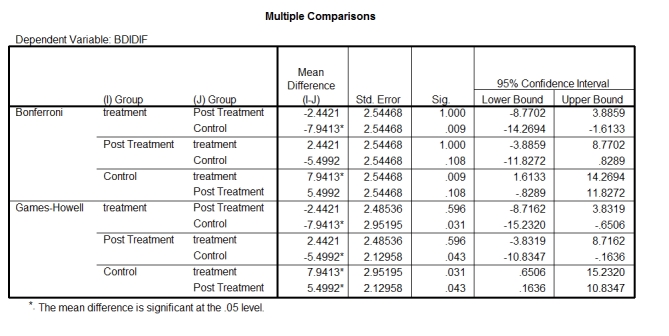
A)The treatment group was significantly different from the control group but not the post-treatment group, and the post-treatment group was significantly different from the control group.
B)The treatment group was significantly different from the post-treatment and control group, and the post-treatment group was significantly different from the control group.
C)The treatment group was significantly different from the control group but not the post-treatment group, and the post-treatment group was not significantly different from the control group.
D)The post hoc tests are inconclusive.
-Based on the output for these tests, what should the researcher conclude? Test of Homogeneity of Variances
BDIDIF

A)The treatment group was significantly different from the control group but not the post-treatment group, and the post-treatment group was significantly different from the control group.
B)The treatment group was significantly different from the post-treatment and control group, and the post-treatment group was significantly different from the control group.
C)The treatment group was significantly different from the control group but not the post-treatment group, and the post-treatment group was not significantly different from the control group.
D)The post hoc tests are inconclusive.

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
16
When conducting a one-way independent ANOVA with three levels on the independent variable, an F-ratio that is large enough to be statistically significant tells us:
A)That the model fitted to the data accounts for less variation than extraneous factors, but it doesn't tell us where the differences between groups lie.
B)That there is a significant three-way interaction.
C)That all of the differences between means are statistically significant.
D)That one or more of the differences between means is statistically significant but not where the differences between groups lie.
A)That the model fitted to the data accounts for less variation than extraneous factors, but it doesn't tell us where the differences between groups lie.
B)That there is a significant three-way interaction.
C)That all of the differences between means are statistically significant.
D)That one or more of the differences between means is statistically significant but not where the differences between groups lie.

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
17
Of the tests below, which tests that the group means are a better fit of the data than the grand mean?
A)Both the repeated-measures and independent ANOVA
B)The independent ANOVA only
C)The dependent ANOVA only
D)Friedman's ANOVA
A)Both the repeated-measures and independent ANOVA
B)The independent ANOVA only
C)The dependent ANOVA only
D)Friedman's ANOVA

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
18
What is the F-statistic?
A)It is a ratio of how good the model is in comparison to how bad it is and therefore it tests the overall goodness of fit of a non- linear model.
B)It is an indicator of variance of error in a linear model.
C)It is an indicator of distribution of predictors within a linear model.
D)It is a ratio of how good the model is in comparison to how bad it is and therefore it tests the overall goodness of fit of a linear model.
A)It is a ratio of how good the model is in comparison to how bad it is and therefore it tests the overall goodness of fit of a non- linear model.
B)It is an indicator of variance of error in a linear model.
C)It is an indicator of distribution of predictors within a linear model.
D)It is a ratio of how good the model is in comparison to how bad it is and therefore it tests the overall goodness of fit of a linear model.

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
19
The student welfare office was interested in trying to enhance students' exam performance by investigating the effects of various interventions. They took five groups of students before their statistics exams and gave them one of five interventions: (1) a control group just sat in a room contemplating the task ahead (Control); (2) the second group had a yoga class to relax them (Yoga); (3) the third group were told they would get monetary rewards contingent upon the grade they received in the exam (Bribes); (4) the fourth group were given beta-blockers to calm their nerves (Beta-Blockers); and (5) the fifth group were encouraged to sit around winding each other up about how much revision they had/hadn't done (You're all going to fail). The student welfare office made four predictions: (1) all interventions should be different from the control; (2) yoga, bribery and beta-blockers should lead to higher exam scores than panic; (3) yoga and bribery should have different effects than the beta-blocker drugs; and (4) yoga and bribery should also differ. Which of the following planned contrasts (with the appropriate group codings) are correct to test these hypotheses?
A)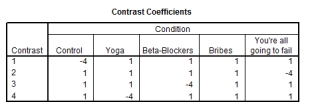
B)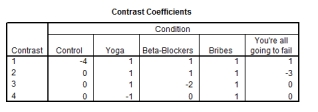
C)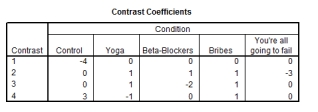
D)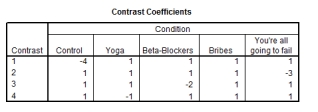
A)

B)

C)

D)


Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
20
What kind of trend does the following graph show? 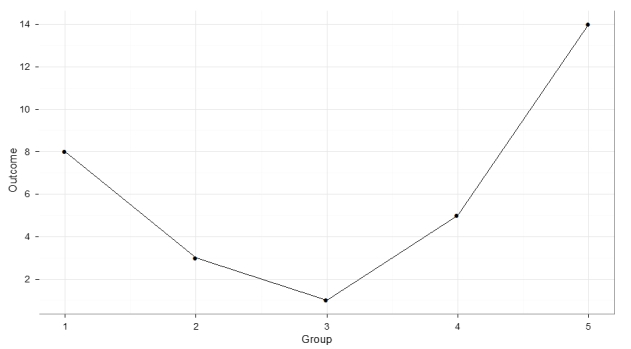
A)Cubic
B)Quartic
C)Quadratic
D)Linear

A)Cubic
B)Quartic
C)Quadratic
D)Linear

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
21
Robust ANOVA tests are able to work with which two data 'violations'?
A)Outliers and homogeneity.
B)Heteroscedasticity and Type I errors.
C)Outliers and heteroscedasticity.
D)Homogeneity and Type II errors.
A)Outliers and homogeneity.
B)Heteroscedasticity and Type I errors.
C)Outliers and heteroscedasticity.
D)Homogeneity and Type II errors.

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
22
A health researcher was interested in the variation of patient recovery rates across four different treatment programmes. He was particularly interested in whether the treatment programme that the patient was in had a possible influence on the patient's recovery rate. He ran an ANOVA with the predictor variable 'treatment programme', which had three categories, 'Placebo', 'Drug X' and 'Natural'; the outcome variable was 'Patient recovery rate'. His ANOVA had an F-statistic of 98.12 (p 0.02). How would you interpret his findings?
A)There is no significant difference in patient recovery rates by treatment programme.
B)There is insufficient information; the results of Post hoc tests are needed.
C)There is a significant difference in patient recovery rates by treatment programme.
D)The results are ambiguous.
A)There is no significant difference in patient recovery rates by treatment programme.
B)There is insufficient information; the results of Post hoc tests are needed.
C)There is a significant difference in patient recovery rates by treatment programme.
D)The results are ambiguous.

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
23
What are post hoc tests?
A)They are tests, which conduct stepwise contrasts, contrasting all the different combination of groups within an ANOVA, through a comparison of each standard deviation against all the others.
B)They are tests, which conduct pairwise contrasts, examining all the different combination of groups within an ANOVA, through a comparison of each group's effect size against all the others.
C)They are tests, which conduct pairwise comparisons, contrasting all the different combination of groups within an ANOVA, through a comparison of each standard error against all the others.
D)They are tests, which conduct pairwise comparisons, comparing all the different combinations of groups within an ANOVA, through a comparison of each mean against all the others.
A)They are tests, which conduct stepwise contrasts, contrasting all the different combination of groups within an ANOVA, through a comparison of each standard deviation against all the others.
B)They are tests, which conduct pairwise contrasts, examining all the different combination of groups within an ANOVA, through a comparison of each group's effect size against all the others.
C)They are tests, which conduct pairwise comparisons, contrasting all the different combination of groups within an ANOVA, through a comparison of each standard error against all the others.
D)They are tests, which conduct pairwise comparisons, comparing all the different combinations of groups within an ANOVA, through a comparison of each mean against all the others.

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
24
What condition can make Post Hoc tests less robust?
A)Equal group sizes.
B)Effect sizes.
C)Outliers and heteroscedasticity.
D)Homoscedasticity.
A)Equal group sizes.
B)Effect sizes.
C)Outliers and heteroscedasticity.
D)Homoscedasticity.

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
25
A teacher in a school was interested in examining the differences in children's maths scores across a year group, which consisted of three classes. She was particularly interested in whether the class the child was in had a possible influence on the child's maths score. She ran an ANOVA with the predictor variable 'class', which had three categories, 'Yellow Class', 'Green Class' and 'Purple class'; the outcome variable was 'maths score'. Her ANOVA had an F-statistic of 4.23 (p 0.68). How would you interpret her findings?
A)There is a significant difference in children's maths scores by class membership.
B)There is no significant difference in children's maths scores by class membership.
C)There is insufficient information; the results of Post hoc tests is needed.
D)The results are ambiguous.
A)There is a significant difference in children's maths scores by class membership.
B)There is no significant difference in children's maths scores by class membership.
C)There is insufficient information; the results of Post hoc tests is needed.
D)The results are ambiguous.

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
26
A business analyst was interested in the variation of sales income across four shops in a retail chain. He ran an ANOVA with the predictor variable 'shop location', which had four categories, 'High street', 'Outlet', 'Online' and 'Suburb'; the outcome variable was 'monthly sales income'. His ANOVA had an F-statistic of 98.12 (p 0.02). How would you interpret his findings?
A)There is no significant difference in monthly sales income by shop location
B)There is a significant difference in monthly sales income by shop location.
C)There is insufficient information; the results of Post hoc tests are needed.
D)The results are ambiguous.
A)There is no significant difference in monthly sales income by shop location
B)There is a significant difference in monthly sales income by shop location.
C)There is insufficient information; the results of Post hoc tests are needed.
D)The results are ambiguous.

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
27
A sports coach running a junior coaching programme was interested in examining the differences in children's fitness performance scores across four different coaching regimes. She was particularly interested in whether the regime the child was in had a possible influence on the child's fitness performance score. She ran an ANOVA with the predictor variable 'coaching regime', which had four categories, 'Yellow group', 'Green group', 'Pink group' and 'Purple group'; the outcome variable was 'fitness performance score'. Her ANOVA had an F-statistic of 98.12 (p 0.02). How would you interpret her findings?
A)There is a significant difference in children's fitness performance score by coaching regime.
B)There is no significant difference in children's fitness performance score by coaching regime.
C)There is insufficient information; the results of Post hoc tests are needed.
D)The results are ambiguous.
A)There is a significant difference in children's fitness performance score by coaching regime.
B)There is no significant difference in children's fitness performance score by coaching regime.
C)There is insufficient information; the results of Post hoc tests are needed.
D)The results are ambiguous.

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
28
Identify two robust tests for identifying homogeneity.
A)Welch's F and Field's F.
B)Browne-Forsythe F and Kruskal-Wallis F.
C)Welch's F and Browne-Forsythe F.
D)Mauchly's F and Field's F.
A)Welch's F and Field's F.
B)Browne-Forsythe F and Kruskal-Wallis F.
C)Welch's F and Browne-Forsythe F.
D)Mauchly's F and Field's F.

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck


