Deck 5: Applications of the Exponential and Natural Logarithm Functions
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/73
Play
Full screen (f)
Deck 5: Applications of the Exponential and Natural Logarithm Functions
1
has a half life of 5730 years. How old is a piece of charcoal which has lost 90% of its ?
A) 20,000 years
B) 11,109 years
C) 9100 years
D) 19,109 years
E) none of these
A) 20,000 years
B) 11,109 years
C) 9100 years
D) 19,109 years
E) none of these
19,109 years
2
A radioactive substance is observed to disintegrate at a rate such that of the original amount remains after one year. What is the half-life of the substance?
A) 0.301 yr
B) 0.588 yr
C) 0.556 yr
D) 6.579 yr
A) 0.301 yr
B) 0.588 yr
C) 0.556 yr
D) 6.579 yr
6.579 yr
3
A country has a population of 287 million in 2005. Assuming a growth rate of 1.3%, determine the function that expresses the population of the country t years after 2005.
A) P(t) = 287
B) P(t) = 287
C) P(t) = 287
D) P(t) = 287
E) none of these
A) P(t) = 287
B) P(t) = 287
C) P(t) = 287
D) P(t) = 287
E) none of these
P(t) = 287
4
Plutonium has a decay rate of 0.003% per year. What is the half life?
A) 2310 years
B) 23,100 years
C) 33,000 years
D) 1630 years
A) 2310 years
B) 23,100 years
C) 33,000 years
D) 1630 years

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
5
Assume that a culture of bacteria grows at a rate proportional to its size such that if 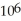 bacteria are present initially, then there are 2 ×
bacteria are present initially, then there are 2 × 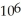 bacteria present after 3 hours. Determine a formula for the number of bacteria present after t hours in terms of powers of 2. (Hint: Recall that
bacteria present after 3 hours. Determine a formula for the number of bacteria present after t hours in terms of powers of 2. (Hint: Recall that 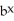 =
= 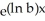 .)Enter your answer exactly in the form
.)Enter your answer exactly in the form 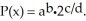
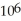 bacteria are present initially, then there are 2 ×
bacteria are present initially, then there are 2 × 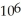 bacteria present after 3 hours. Determine a formula for the number of bacteria present after t hours in terms of powers of 2. (Hint: Recall that
bacteria present after 3 hours. Determine a formula for the number of bacteria present after t hours in terms of powers of 2. (Hint: Recall that 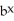 =
= 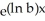 .)Enter your answer exactly in the form
.)Enter your answer exactly in the form 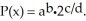

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
6
In a certain country, the rate of increase of the population is proportional to the population P(t). In fact, Suppose that initially the country's population is 50,000, and that 10 years later there are 500,000 people. Which of the following equations expresses this information mathematically?
A) 10 =
B) 500 =
C) 500,000 =
D) 500,000 = 50,000
E) none of these
A) 10 =
B) 500 =
C) 500,000 =
D) 500,000 = 50,000
E) none of these

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
7
The size of an insect colony t days after its formation is P( t) = 1000 . Approximately how many insects are present after 10 days?
A) 690
B) 7389
C) 54,598
D) 6900
E) none of these
A) 690
B) 7389
C) 54,598
D) 6900
E) none of these

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
8
A bacterial culture grows exponentially; that is, P(t) = 100 , where P(t) is the size of the culture at time t hours. Suppose that after 2 hours the size of the culture is 400. What is k (approximately)?
A) 3
B) 0.69
C) 0.06
D) 0.48
E) none of these
A) 3
B) 0.69
C) 0.06
D) 0.48
E) none of these

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
9
Suppose that a school of fish in a pond grows according to the exponential law 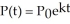 and suppose that the size of the colony triples in 24 days. Determine k.
and suppose that the size of the colony triples in 24 days. Determine k.
Enter your answer exactly in the form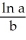 where a, b are integers.
where a, b are integers.
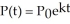 and suppose that the size of the colony triples in 24 days. Determine k.
and suppose that the size of the colony triples in 24 days. Determine k.Enter your answer exactly in the form
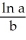 where a, b are integers.
where a, b are integers.
Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
10
Radioactive carbon 11 has a half-life of 20 minutes. If there are 200 grams present at the start of our experiment, how many grams will remain after 10 minutes?
A) 141.421 g
B) 6.931 g
C) 50 g
D) 100 g
A) 141.421 g
B) 6.931 g
C) 50 g
D) 100 g

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
11
A parchment is offered for sale at a Paris flea market. The owner claims it is at least 2000 years old. However, a carbon-dating test shows that 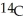 -
- 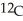 ratio for the manuscript is 95% of the corresponding ratio for currently manufactured parchment. How old is the manuscript? (The decay constant of
ratio for the manuscript is 95% of the corresponding ratio for currently manufactured parchment. How old is the manuscript? (The decay constant of 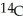 is 0.00012)Enter your answer exactly in the form
is 0.00012)Enter your answer exactly in the form 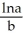 (no units).
(no units).
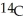 -
- 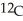 ratio for the manuscript is 95% of the corresponding ratio for currently manufactured parchment. How old is the manuscript? (The decay constant of
ratio for the manuscript is 95% of the corresponding ratio for currently manufactured parchment. How old is the manuscript? (The decay constant of 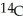 is 0.00012)Enter your answer exactly in the form
is 0.00012)Enter your answer exactly in the form 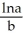 (no units).
(no units).
Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
12
A certain radioactive substance is decaying at a rate proportional to the amount present. If 100 grams decays to 13.5 grams in 4 years, how long will it take for 90 grams to decay to 30 grams?
A) 2.405 yr
B) 2.195 yr
C) 0.501 yr
D) Problem cannot be solved as stated.
A) 2.405 yr
B) 2.195 yr
C) 0.501 yr
D) Problem cannot be solved as stated.

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
13
A colony of bacteria is growing at a rate proportional to the number of bacteria present. At the beginning of an experiment there were about 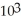 bacteria present. In two hours, the count rose to
bacteria present. In two hours, the count rose to 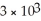 bacteria. At what time will there be 6 ×
bacteria. At what time will there be 6 × 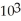 bacteria present?
bacteria present?
Enter just a real number rounded up to one decimal place (no units).
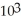 bacteria present. In two hours, the count rose to
bacteria present. In two hours, the count rose to 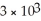 bacteria. At what time will there be 6 ×
bacteria. At what time will there be 6 × 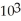 bacteria present?
bacteria present?Enter just a real number rounded up to one decimal place (no units).

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
14
Suppose that at any time t, a colony of fruit flies is growing at a rate equal to one half the current size of the colony. Find a formula which gives the size of the colony at time t if there were originally 500 fruit flies present.
Enter your answer exactly in the form: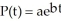
Enter your answer exactly in the form:
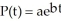

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
15
Suppose that a school of fish in a pond grows according to the exponential law 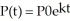 and suppose that the size of the colony triples in 24 days. If the initial size of the school was 50, when will the school contain 200 fish? Enter your answer exactly in the form
and suppose that the size of the colony triples in 24 days. If the initial size of the school was 50, when will the school contain 200 fish? Enter your answer exactly in the form 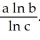
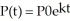 and suppose that the size of the colony triples in 24 days. If the initial size of the school was 50, when will the school contain 200 fish? Enter your answer exactly in the form
and suppose that the size of the colony triples in 24 days. If the initial size of the school was 50, when will the school contain 200 fish? Enter your answer exactly in the form 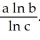

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
16
A certain radioactive element has a half-life of 12 minutes. At what time is the substance decaying at a rate of 3.466 grams per minute if there are 120 grams present initially?
A) t = 0
B) t = 0.693 min
C) t = 0.058 min
D) t = 12 min
A) t = 0
B) t = 0.693 min
C) t = 0.058 min
D) t = 12 min

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
17
Let P(t) be the quantity of strontium-90 remaining after t years. Suppose the half-life of strontium-90 is 28 years. Which of the following equations expresses the half-life information?
A) P(28) =
B) P = 28
C) 28 =
D) 28 =
E) none of these
A) P(28) =
B) P = 28
C) 28 =
D) 28 =
E) none of these

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
18
The population of a certain region was 10 million in 1950. By 1970, it had increased to 13.5 million. Assuming exponential growth, estimate the population in the year 2000.
Enter your answer exactly in the form a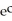 (no units).
(no units).
Enter your answer exactly in the form a
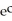 (no units).
(no units).
Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
19
The population of a colony of bacteria triples in 3 days. Assuming that the rate of growth is proportional to the size of the population, how long did it take for the colony to double in size?
A) 2 days
B) 1.9 days
C) 4.9 days
D) 6 days
E) none of these
A) 2 days
B) 1.9 days
C) 4.9 days
D) 6 days
E) none of these

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
20
Sixteen pounds of a radioactive substance loses one fourth of its original mass in 2 days. The mass m(t) remaining at time t is given by:
A) m(t) = 16
B) m(t) = 16
C) m(t) = 4
D) m(t) = 16
A) m(t) = 16
B) m(t) = 16
C) m(t) = 4
D) m(t) = 16

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
21
Carbon 14 has a half-life of 5730 years. Determine its decay constant.
Enter just a real number rounded to five decimal places.
Enter just a real number rounded to five decimal places.

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
22
A bank pays 2.5% interest on deposits. What is the return on a $1000 deposit after two years if interest is compounded continuously?
A) $1051.27
B) $778.80
C) $1648.72
D) $1284.03
E) none of these
A) $1051.27
B) $778.80
C) $1648.72
D) $1284.03
E) none of these

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
23
A fossil was discovered that had about 70% of the 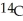 level found today in living matter. Given that the decay constant for
level found today in living matter. Given that the decay constant for 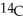 is 0.00012, determine the age of the fossil.
is 0.00012, determine the age of the fossil.
Enter your answer exactly as just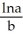 where a is a real number to one decimal place and b is a real number to 5 decimal places.
where a is a real number to one decimal place and b is a real number to 5 decimal places.
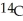 level found today in living matter. Given that the decay constant for
level found today in living matter. Given that the decay constant for 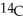 is 0.00012, determine the age of the fossil.
is 0.00012, determine the age of the fossil.Enter your answer exactly as just
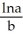 where a is a real number to one decimal place and b is a real number to 5 decimal places.
where a is a real number to one decimal place and b is a real number to 5 decimal places.
Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
24
Barium 140 has a half-life of 13 days. After 25 days a given sample comprises 5 grams. How large was the original sample?
Enter your answer as a real number to two decimal places (no units).
Enter your answer as a real number to two decimal places (no units).

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
25
Potassium has a half-life of 12 hours. How long will it take for a quantity of potassium to decay to 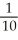 its original size?
its original size?
Enter your answer as a real number rounded to one decimal place (no units).
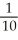 its original size?
its original size?Enter your answer as a real number rounded to one decimal place (no units).

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
26
You deposit $500 in a savings account paying 4% interest continuously compounded. How much will the account be worth after 32 months?
A) $545.20
B) $526.10
C) $576.70
D) $556.20
A) $545.20
B) $526.10
C) $576.70
D) $556.20

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
27
If an investment doubles in 5 years continuously compounded, how long will it take for the investment to triple?
A) 7.93 years
B) 7 years
C) 10 years
D) 7.5 years
A) 7.93 years
B) 7 years
C) 10 years
D) 7.5 years

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
28
Plutonium 239 has a half-life of 24,000 years. What is its decay constant?
Enter your answer as just a real number to eight decimal places.
Enter your answer as just a real number to eight decimal places.

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
29
A high-yield savings pays 20% interest, compounded continuously. How long would it take an initial investment of $2500 to grow to $20,000?
A) 1.04 years
B) 103.972 years
C) 10.397 years
D) 14.979 years
E) none of these
A) 1.04 years
B) 103.972 years
C) 10.397 years
D) 14.979 years
E) none of these

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
30
How long will it take for an investment to triple if interest is paid at 10%, compounded continuously?
A) 30 years
B) 3 years
C) 8.6 years
D) 11 years
E) none of these
A) 30 years
B) 3 years
C) 8.6 years
D) 11 years
E) none of these

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
31
$1,000 is invested at r% interest continuously compounded. After 6 years the account has reached $1350. What was the interest rate?
A) 6%
B) 5.3%
C) 4.8%
D) 5%
A) 6%
B) 5.3%
C) 4.8%
D) 5%

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
32
Krypton 85 gas leaks into the reactor room of an electric power plant. Its half-life is 10 years. How long is it before 99.9% of the krypton decays?
Enter your answer as just a real number rounded to one decimal place (no units).
Enter your answer as just a real number rounded to one decimal place (no units).

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
33
What rate of interest is required in order for a $100 investment to double in 3 years if the interest is compounded continuously?
A) 23.1%
B) 3.05%
C) 5.49%
D) 54.9%
E) none of these
A) 23.1%
B) 3.05%
C) 5.49%
D) 54.9%
E) none of these

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
34
$1000 is invested at 6% interest compounded continuously. What is the value of the investment after 5 years?
A) $1349.86
B) $6691.13
C) $1338.23
D) $1822.12
E) none of these
A) $1349.86
B) $6691.13
C) $1338.23
D) $1822.12
E) none of these

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
35
A savings account paying 3% continuously compounded interest has $1600 after 8 years. How much was initially deposited?
A) $1020
B) $1159
C) $1259
D) $630
A) $1020
B) $1159
C) $1259
D) $630

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
36
The decay constant for strontium 90 is λ = 0.0244, where the time is measured in years. How long will it take for a quantity 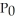 of strontium 90 to decay to
of strontium 90 to decay to  its original size?
its original size?
Enter your answer exactly in the form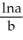 where a is a reduced fraction and b is a real number to four decimal places (no units).
where a is a reduced fraction and b is a real number to four decimal places (no units).
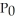 of strontium 90 to decay to
of strontium 90 to decay to  its original size?
its original size?Enter your answer exactly in the form
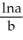 where a is a reduced fraction and b is a real number to four decimal places (no units).
where a is a reduced fraction and b is a real number to four decimal places (no units).
Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
37
A savings account pays 7% interest, compounded continuously. How much should be deposited now in order to have $5000 in the account at the end of five years?
A) $4661.97
B) $2884.75
C) $3523.44
D) $533.83
A) $4661.97
B) $2884.75
C) $3523.44
D) $533.83

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
38
Eight years ago, $2000 was deposited in a savings account paying 3% interest compounded continuously. Three years ago, $500 was withdrawn from the account. What is the current value of the account?
A) $4319.08
B) $2042.50
C) $3964.93
D) $1995.41
A) $4319.08
B) $2042.50
C) $3964.93
D) $1995.41

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
39
How much money has to be invested now at 8% continuous interest in order to have $1000 after 5 years?
A) $461.56
B) $18.32
C) $183.20
D) $670.32
E) none of these
A) $461.56
B) $18.32
C) $183.20
D) $670.32
E) none of these

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
40
It is observed that the sales of a certain recording fall to 75% of their original level one month after advertising stops. If this continues, what will be the sales after 4 months?
Enter just a real number rounded to one decimal place (no units or symbols).
Enter just a real number rounded to one decimal place (no units or symbols).

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
41
Suppose a manufacturer can sell q = 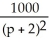 - 6 units of a product when the price is p dollars per unit. Determine the elasticity of demand, E(p), when the price is p = 8 dollars.
- 6 units of a product when the price is p dollars per unit. Determine the elasticity of demand, E(p), when the price is p = 8 dollars.
Enter just an integer.
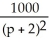 - 6 units of a product when the price is p dollars per unit. Determine the elasticity of demand, E(p), when the price is p = 8 dollars.
- 6 units of a product when the price is p dollars per unit. Determine the elasticity of demand, E(p), when the price is p = 8 dollars.Enter just an integer.

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
42
Let y = 6(1 - ). What is 3(6 - y) ?
A) 12 - 6
B) 18
C) 6 - 6
D) 3
E) none of these
A) 12 - 6
B) 18
C) 6 - 6
D) 3
E) none of these

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
43
Suppose that $500 is deposited in a bank certificate paying 10% interest compounded continuously. How much will the certificate be worth after 5 years? Enter your answer in dollars to two decimal places (no symbols or words).

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
44
Determine the percentage rate of change of f(x) = at x = 15 and x = 30.
A) = 22%, = 5%
B) = 90%, = 90%
C) = 38%, = 14%
D) = 17%, = 29%
A) = 22%, = 5%
B) = 90%, = 90%
C) = 38%, = 14%
D) = 17%, = 29%

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
45
Suppose that the value of a certain investment after t years can be approximated by the function 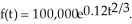 What is the dollar value of the investment after 8 years?
What is the dollar value of the investment after 8 years?
Enter your answer exactly in the form: a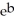 where a is an integer and b is a real number to two decimal places (no units).
where a is an integer and b is a real number to two decimal places (no units).
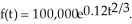 What is the dollar value of the investment after 8 years?
What is the dollar value of the investment after 8 years?Enter your answer exactly in the form: a
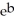 where a is an integer and b is a real number to two decimal places (no units).
where a is an integer and b is a real number to two decimal places (no units).
Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
46
A manufacturer has a demand function q = 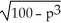 . Determine the elasticity of demand as a function of p.
. Determine the elasticity of demand as a function of p.
Enter your answer exactly as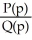 where P, Q are polynomials in p in standard form, and the leading coefficient of P is a reduced fraction of form
where P, Q are polynomials in p in standard form, and the leading coefficient of P is a reduced fraction of form 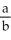 .
.
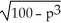 . Determine the elasticity of demand as a function of p.
. Determine the elasticity of demand as a function of p.Enter your answer exactly as
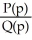 where P, Q are polynomials in p in standard form, and the leading coefficient of P is a reduced fraction of form
where P, Q are polynomials in p in standard form, and the leading coefficient of P is a reduced fraction of form 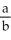 .
.
Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
47
For the demand function q = , find E(p) and determine if the demand is elastic or inelastic (or neither) at the price p = 5.
A) E(p) = 2 - p, inelastic
B) E(p) = p - 2, elastic
C) E(p) = p - 2, inelastic
D) E(p) = 2 - p, elastic
A) E(p) = 2 - p, inelastic
B) E(p) = p - 2, elastic
C) E(p) = p - 2, inelastic
D) E(p) = 2 - p, elastic

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
48
Mr. Jones has two investments. The first is currently worth $50,000 and has an annual yield of 10% compounded continuously. The second is currently worth $70,000 and has an annual yield of 8% compounded continuously. After how many years will the two investments be worth the same amount? Enter your answer in years to one decimal place (no units).

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
49
Determine the percentage rate of change of F(t) = at t = 1 and t = 5.
A) = 18%, = 90%
B) = -18%, = -90%
C) = 19%, = 70%
D)
A) = 18%, = 90%
B) = -18%, = -90%
C) = 19%, = 70%
D)

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
50
How long is required for an investment of $2000 to double if the interest is 10% compounded continuously? Enter your answer in years to one decimal place 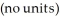

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
51
A high school student deposits a $500 graduation gift in a bank account that pays 4.8% interest compounded continuously. How much will the account be worth after 18 months?
A) $1123.95
B) $1027.22
C) $973.71
D) $1162.71
E) none of these
A) $1123.95
B) $1027.22
C) $973.71
D) $1162.71
E) none of these

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
52
Determine the percentage rate of change of h(p) = at p = 1 and p = 9.
A) = 40%, = 6%
B) = -70%, = -11%
C) = -40%, = -6%
D) = 70%, = 11%
A) = 40%, = 6%
B) = -70%, = -11%
C) = -40%, = -6%
D) = 70%, = 11%

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
53
For the demand function q = 150(245 - ), find E(p) and determine if the demand is elastic or inelastic (or neither) at the price p =7.
A) E(p) = , elastic
B) E(p) = , elastic
C) E(p) = , inelastic
D) E(p) = , inelastic
A) E(p) = , elastic
B) E(p) = , elastic
C) E(p) = , inelastic
D) E(p) = , inelastic

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
54
Determine the percentage rate of change of f(t) = 2 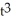 at t = 5.
at t = 5.
Enter your answer as just a reduced fraction of form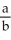 .
.
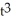 at t = 5.
at t = 5.Enter your answer as just a reduced fraction of form
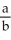 .
.
Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
55
What is the present value of an investment of $1000 payable at the end of 10 years at a 9% rate of interest compounded continuously? Enter your answer in dollars to two decimal places (no symbols or words).

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
56
Suppose that the value in billions of dollars of a company is determined to be 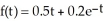 where t is measured in years. What is the percentage rate of growth of the company at time t = 0?
where t is measured in years. What is the percentage rate of growth of the company at time t = 0?
Enter just an integer (no units).
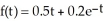 where t is measured in years. What is the percentage rate of growth of the company at time t = 0?
where t is measured in years. What is the percentage rate of growth of the company at time t = 0?Enter just an integer (no units).

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
57
Which of the following functions satisfy the differential equation y' = 3(12 - y)?
(I) y = 4(3 - )
(II) y = 12(1 - )
(III) y = 12 -
(IV) y = 3(1 - )
A) I, II, and III
B) I and II
C) I and III
D) II and III
E) none of these
(I) y = 4(3 - )
(II) y = 12(1 - )
(III) y = 12 -
(IV) y = 3(1 - )
A) I, II, and III
B) I and II
C) I and III
D) II and III
E) none of these

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
58
What rate of interest will make an investment triple in 8 years if the interest is compounded continuously? Enter your answer as a percent to one decimal place 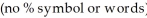
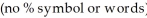

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
59
A company has a demand function q= 200 - 40p. Determine the elasticity of demand as a function of p. Enter your answer exactly as 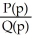 where P, Q are polynomials in p in standard form.
where P, Q are polynomials in p in standard form.
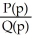 where P, Q are polynomials in p in standard form.
where P, Q are polynomials in p in standard form.
Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
60
In a town of 10,000 people, the number of people who during each day first hear the news of a local tax increase is one-tenth the number of people who have not yet heard the news. If f(t) stands for the number of informed people in the town, what is the differential equation f(t) satisfies?
A) f'(t) + f(t) = 10,000
B) f(t) =
C) f'(t) = (10,000 - f(t))
D) f'(t) = f(t)
E) none of these
A) f'(t) + f(t) = 10,000
B) f(t) =
C) f'(t) = (10,000 - f(t))
D) f'(t) = f(t)
E) none of these

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
61
A rumor is spread by word of mouth to a potential audience of 3000 people. After t days, 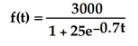 people will have heard the rumor. The graphs are shown below.
people will have heard the rumor. The graphs are shown below.
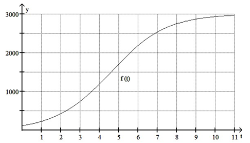
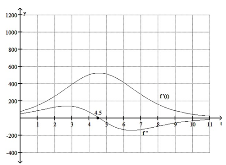
At what rate will the rumor be spreading when half of the potential audience has heard the rumor? Enter just an integer rounded to the nearest hundred (no units).
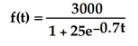 people will have heard the rumor. The graphs are shown below.
people will have heard the rumor. The graphs are shown below.

At what rate will the rumor be spreading when half of the potential audience has heard the rumor? Enter just an integer rounded to the nearest hundred (no units).

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
62
A rumor is spread by word of mouth to a potential audience of 3000 people. After t days, 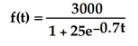 people will have heard the rumor. The graphs are shown below.
people will have heard the rumor. The graphs are shown below.


Approximately when will 1250 people have heard the rumor? Enter just an integer (no units).
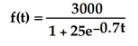 people will have heard the rumor. The graphs are shown below.
people will have heard the rumor. The graphs are shown below.

Approximately when will 1250 people have heard the rumor? Enter just an integer (no units).

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
63
A rumor is spread by word of mouth to a potential audience of 3000 people. After t days, 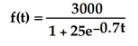 people will have heard the rumor. The graphs are shown below.
people will have heard the rumor. The graphs are shown below.


Approximately when will the rumor be spreading at a rate of 200 people per day? Enter just two integers a, b where a< (round to the nearest integers).
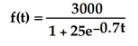 people will have heard the rumor. The graphs are shown below.
people will have heard the rumor. The graphs are shown below.

Approximately when will the rumor be spreading at a rate of 200 people per day? Enter just two integers a, b where a< (round to the nearest integers).

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
64
A rumor is spread by word of mouth to a potential audience of 3000 people. After t days, 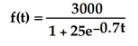 people will have heard the rumor. The graphs are shown below.
people will have heard the rumor. The graphs are shown below.


At approximately what rate will the rumor be spreading after 7 days? Enter just an integer rounded to the nearest hundred (no words or units).
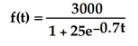 people will have heard the rumor. The graphs are shown below.
people will have heard the rumor. The graphs are shown below.

At approximately what rate will the rumor be spreading after 7 days? Enter just an integer rounded to the nearest hundred (no words or units).

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
65
If the relative rate of change of a function f is always 5, what kind of equation will f be represented by? Enter your answer in the form: f(t) = C 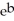 (leave C in your answer).
(leave C in your answer).
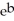 (leave C in your answer).
(leave C in your answer).
Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
66
If y = 10(1 - 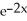 ) and y' = a -2y, find a.
) and y' = a -2y, find a.
Enter just an integer.
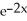 ) and y' = a -2y, find a.
) and y' = a -2y, find a.Enter just an integer.

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
67
A rumor is spread by word of mouth to a potential audience of 3000 people. After t days, 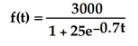 people will have heard the rumor. The graphs are shown below.
people will have heard the rumor. The graphs are shown below.


Approximately how many people will have heard the rumor after 7 days? Enter your answer as just an integer rounded to the nearest hundred.
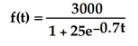 people will have heard the rumor. The graphs are shown below.
people will have heard the rumor. The graphs are shown below.

Approximately how many people will have heard the rumor after 7 days? Enter your answer as just an integer rounded to the nearest hundred.

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
68
A rumor is spread by word of mouth to a potential audience of 3000 people. After t days, 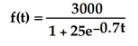 people will have heard the rumor. The graphs are shown below.
people will have heard the rumor. The graphs are shown below.


When will the rumor be spreading at the greatest rate? Enter just an integer (round to the nearest integer, no units)
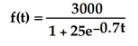 people will have heard the rumor. The graphs are shown below.
people will have heard the rumor. The graphs are shown below.

When will the rumor be spreading at the greatest rate? Enter just an integer (round to the nearest integer, no units)

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
69
Let g(t) = 100 - 100 be the number of cases of measles in a certain school t days after the first case is reported. Which of the following best describes the spread of the disease?
A) The number of cases decreases according to exponential decay.
B) After the first day there are 100 cases, after which the number of cases decreases daily to 0.
C) Initially, the disease spreads quickly, but then the rate of increase slows so that the number of cases never exceeds 100.
D) The disease spreads quickly until the number of cases reaches 100; then gradually the number of cases decreases.
E) none of these
A) The number of cases decreases according to exponential decay.
B) After the first day there are 100 cases, after which the number of cases decreases daily to 0.
C) Initially, the disease spreads quickly, but then the rate of increase slows so that the number of cases never exceeds 100.
D) The disease spreads quickly until the number of cases reaches 100; then gradually the number of cases decreases.
E) none of these

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
70
If y = 2(1 - 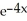 ) and y' = 4 - by, find b.
) and y' = 4 - by, find b.
Enter just an integer.
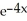 ) and y' = 4 - by, find b.
) and y' = 4 - by, find b.Enter just an integer.

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
71
Let A'(t) = 0.3(25,000 - A(t)), A(0) = 0. Which of the following is the formula for A(t)?
A) A(t) = 25,000(1 - )
B) A(t) = 25,000
C) A(t) = 25,000(1 - 0.3t)
D) A(t) = 25,000
E) none of these
A) A(t) = 25,000(1 - )
B) A(t) = 25,000
C) A(t) = 25,000(1 - 0.3t)
D) A(t) = 25,000
E) none of these

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
72
Find a so that y = 1 - a 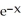 solves the differential equation
solves the differential equation 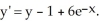 Enter just an integer.
Enter just an integer.
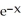 solves the differential equation
solves the differential equation 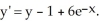 Enter just an integer.
Enter just an integer.
Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
73
Find a so that y = 1 + 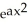 solves the differential equation
solves the differential equation 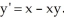 Enter just a reduced fraction of form
Enter just a reduced fraction of form 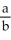 .
.
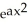 solves the differential equation
solves the differential equation 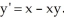 Enter just a reduced fraction of form
Enter just a reduced fraction of form 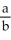 .
.
Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck


