Deck 16: Atoms
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/128
Play
Full screen (f)
Deck 16: Atoms
1
The first Bohr radius, r0, is 0.0529 nm and the corresponding energy, E0, is 13.6 eV. The wavelength of the light emitted as a hydrogen atom undergoes a transition from state n = 4 to n = 2 is
A) 656 nm
B) 486 nm
C) 434 nm
D) 410 nm
E) None of these is correct.
A) 656 nm
B) 486 nm
C) 434 nm
D) 410 nm
E) None of these is correct.
486 nm
2
The wavelength of the visible line in the hydrogen spectrum that corresponds to m = 5 in the Balmer equation is
A) 656 nm
B) 486 nm
C) 434 nm
D) 410 nm
E) None of these is correct.
A) 656 nm
B) 486 nm
C) 434 nm
D) 410 nm
E) None of these is correct.
434 nm
3
The order-of-magnitude of the diameter of an atom is closest to
A) 10-6 m
B) 10-8 m
C) 10-10 m
D) 10-12 m
E) 10-14 m
A) 10-6 m
B) 10-8 m
C) 10-10 m
D) 10-12 m
E) 10-14 m
10-10 m
4
The constant in the Rydberg-Ritz formula is RH = 10.96776 µm-1. The wavelength predicted by this formula for n1 = 5 and n2 = 3 is
A) 656 nm
B) 486 nm
C) 434 nm
D) 410 nm
E) None of these is correct.
A) 656 nm
B) 486 nm
C) 434 nm
D) 410 nm
E) None of these is correct.

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
5
The wavelength of the visible line in the hydrogen spectrum that corresponds to m = 4 in the Balmer equation is
A) 656 nm
B) 486 nm
C) 434 nm
D) 410 nm
E) None of these is correct.
A) 656 nm
B) 486 nm
C) 434 nm
D) 410 nm
E) None of these is correct.

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
6
The constant in the Rydberg-Ritz formula is RH = 10.96776 µm-1. The wavelength predicted by this formula for n1 = 3 and n2 = 2 is
A) 656 nm
B) 486 nm
C) 434 nm
D) 410 nm
E) None of these is correct.
A) 656 nm
B) 486 nm
C) 434 nm
D) 410 nm
E) None of these is correct.

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
7
If the potential energy of an electron in the Bohr's model is -U0, then the kinetic energy and the total energy of the electron are, respectively,
A) U0 and 0.5U0
B) 0.5U0 and -0.5U0
C) 0.5U0 and 0.5U0
D) U0 and -0.5U0
E) 0.5U0 and U0
A) U0 and 0.5U0
B) 0.5U0 and -0.5U0
C) 0.5U0 and 0.5U0
D) U0 and -0.5U0
E) 0.5U0 and U0

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
8
The binding energy of hydrogen is 13.6 eV. The wavelength of the emission line corresponding to the transition from n = 4 to n = 3 is
A) 1.9 *10-6 m
B) 8.2 * 10-7 m
C) 5.3 * 105 m
D) 3.0 * 10-25 m
E) 1.6 * 1014 m
A) 1.9 *10-6 m
B) 8.2 * 10-7 m
C) 5.3 * 105 m
D) 3.0 * 10-25 m
E) 1.6 * 1014 m

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
9
The critical experiments that established the nuclear nature of atoms were performed by
A) Bohr
B) Balmer
C) Rydberg and Ritz
D) Geiger and Marsden
E) Thomson
A) Bohr
B) Balmer
C) Rydberg and Ritz
D) Geiger and Marsden
E) Thomson

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
10
The order-of-magnitude of the diameter of the nucleus is closest to
A) 10-6 m
B) 10-8 m
C) 10-10 m
D) 10-12 m
E) 10-15 m
A) 10-6 m
B) 10-8 m
C) 10-10 m
D) 10-12 m
E) 10-15 m

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
11
According to the Bohr theory, a hydrogen atom
A) does not radiate when it is in a stationary state.
B) radiates when the electron accelerates in a circular orbit.
C) remains in the ground state until it gives off a photon.
D) gives off a continuous spectrum from the K-shell.
E) has an electron in the ground state, an electron in the n = 1 state, an electron in the
N = 2 state, and so on.
A) does not radiate when it is in a stationary state.
B) radiates when the electron accelerates in a circular orbit.
C) remains in the ground state until it gives off a photon.
D) gives off a continuous spectrum from the K-shell.
E) has an electron in the ground state, an electron in the n = 1 state, an electron in the
N = 2 state, and so on.

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
12
Which of the following statements is true?
A) The size of the nucleus of an atom is 5 times smaller than the size of the atom.
B) The size of an atom is determined by the electron cloud.
C) Most of an atom is empty space.
D) The mass of an atom is determined primarily by the mass of the nucleus.
E) All of these are correct.
A) The size of the nucleus of an atom is 5 times smaller than the size of the atom.
B) The size of an atom is determined by the electron cloud.
C) Most of an atom is empty space.
D) The mass of an atom is determined primarily by the mass of the nucleus.
E) All of these are correct.

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
13
In the Bohr model of the atom
A) gravitational forces play a significant role.
B) electrons do not radiate energy when they are in a stable orbit.
C) the electrons spiral into the nucleus.
D) the energy of an electron in a stable orbit is an integral multiple of h/(2 ).
E) None of these is correct.
A) gravitational forces play a significant role.
B) electrons do not radiate energy when they are in a stable orbit.
C) the electrons spiral into the nucleus.
D) the energy of an electron in a stable orbit is an integral multiple of h/(2 ).
E) None of these is correct.

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
14
The binding energy of a hydrogen atom is inversely proportional to the square of the principal quantum number n. The binding energy of the ground level of atomic hydrogen is 13.6 eV. The binding energy of the second (n = 2) level of the hydrogen atom is
A) +13.6 eV
B) -13.6 eV
C) -3.4 eV
D) -54.8 eV
E) +3.4 eV
A) +13.6 eV
B) -13.6 eV
C) -3.4 eV
D) -54.8 eV
E) +3.4 eV

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
15
The kinetic energy of an electron moving in a circular orbit of radius r about a positive charge Ze varies
A) directly with r.
B) directly with r2.
C) indirectly with r.
D) indirectly with r2.
E) indirectly with r1/2.
A) directly with r.
B) directly with r2.
C) indirectly with r.
D) indirectly with r2.
E) indirectly with r1/2.

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
16
The first Bohr radius, r0, is 0.0529 nm and the corresponding energy, E0, is 13.6 eV. The wavelength of the light emitted as a hydrogen atom undergoes a transition from state n = 3 to n = 2 is
A) 656 nm
B) 486 nm
C) 434 nm
D) 410 nm
E) None of these is correct.
A) 656 nm
B) 486 nm
C) 434 nm
D) 410 nm
E) None of these is correct.

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
17
When a gold foil is bombarded with alpha particles, a small fraction of the alpha particles were scattered at large angles. The large scattering angles
A) suggested that the positive charges in an atom were uniformly distributed throughout the atom.
B) were consistent with all of the negative charge of the atom being concentrated at the center of the atom.
C) suggested that the negative charges in an atom were uniformly distributed throughout the atom.
D) required that the positive charge and most of the mass of the atom be concentrated in a very small region.
E) were consistent with the idea that the atom has a neutral nucleus.
A) suggested that the positive charges in an atom were uniformly distributed throughout the atom.
B) were consistent with all of the negative charge of the atom being concentrated at the center of the atom.
C) suggested that the negative charges in an atom were uniformly distributed throughout the atom.
D) required that the positive charge and most of the mass of the atom be concentrated in a very small region.
E) were consistent with the idea that the atom has a neutral nucleus.

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
18
The radius of the n = 1 orbit in the hydrogen atom is 0.053 nm. What is the radius of the n = 3 orbit of lithium, which has three protons in its nucleus?
A) 3(0.053) nm
B) 9(0.053) nm
C) 0.053 nm
D) (1/3)(0.053) nm
E) (1/9)(0.053) nm
A) 3(0.053) nm
B) 9(0.053) nm
C) 0.053 nm
D) (1/3)(0.053) nm
E) (1/9)(0.053) nm

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
19
The radius of the n = 1 Bohr orbit in the hydrogen atom is 0.053 nm. What is the radius of the n = 5 Bohr orbit?
A) 5(0.053) nm
B) 25(0.053) nm
C) 0.053 nm
D) (1/5)(0.053) nm
E) (1/25)(0.053) nm
A) 5(0.053) nm
B) 25(0.053) nm
C) 0.053 nm
D) (1/5)(0.053) nm
E) (1/25)(0.053) nm

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
20
J. J. Thomson's model of an atom
A) had electrons embedded in some kind of fluid that contained most of the mass of the atom.
B) held that the fluid containing most of the mass of the atom had enough positive charge to make the atom electrically neutral.
C) failed to predict the observed frequencies for any atom.
D) depended upon electric forces to produce stability.
E) All of these are correct.
A) had electrons embedded in some kind of fluid that contained most of the mass of the atom.
B) held that the fluid containing most of the mass of the atom had enough positive charge to make the atom electrically neutral.
C) failed to predict the observed frequencies for any atom.
D) depended upon electric forces to produce stability.
E) All of these are correct.

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
21
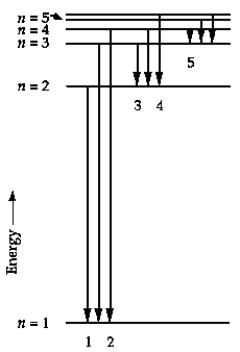 In the energy-level diagram, the line that corresponds to the longest wavelength in the Balmer series is
In the energy-level diagram, the line that corresponds to the longest wavelength in the Balmer series isA) 1
B) 2
C) 3
D) 4
E) 5

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
22
Using Bohr's model, the speed of an electron in the first orbit is
A) 3.14 *105 m/s
B) 1.09 * 106 m/s
C) 1.37 * 107 m/s
D) 2.19 *106 m/s
E) None of these is correct.
A) 3.14 *105 m/s
B) 1.09 * 106 m/s
C) 1.37 * 107 m/s
D) 2.19 *106 m/s
E) None of these is correct.

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
23
The radii of the Bohr orbits in atomic hydrogen are given by 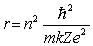 .
.
If the radius of the first Bohr orbit (n = 1) is 0.053 nm, the radius of the third Bohr orbit (n = 3) is
A) 0.16 nm
B) 0.018 nm
C) 0.48 nm
D) 0.35 nm
E) 1.3 nm
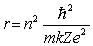 .
.If the radius of the first Bohr orbit (n = 1) is 0.053 nm, the radius of the third Bohr orbit (n = 3) is
A) 0.16 nm
B) 0.018 nm
C) 0.48 nm
D) 0.35 nm
E) 1.3 nm

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
24
Bohr's quantum condition on electron orbits required
A) that the angular momentum of the electron about the hydrogen nucleus equal nh/(2 ).
B) that no more than one electron occupy a given stationary state.
C) the electrons to spiral into the nucleus while radiating electromagnetic waves.
D) that the energies of an electron in a hydrogen atom be equal to nEo, where Eo is a constant energy and n is an integer.
E) None of these is correct.
A) that the angular momentum of the electron about the hydrogen nucleus equal nh/(2 ).
B) that no more than one electron occupy a given stationary state.
C) the electrons to spiral into the nucleus while radiating electromagnetic waves.
D) that the energies of an electron in a hydrogen atom be equal to nEo, where Eo is a constant energy and n is an integer.
E) None of these is correct.

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
25
What is the difference in wavelength between the longest wavelength in the Lyman series and that of the longest wavelength in the Paschen series?
A) 1754 nm
B) 1876 nm
C) 535 nm
D) 1220 nm
E) None of these is correct.
A) 1754 nm
B) 1876 nm
C) 535 nm
D) 1220 nm
E) None of these is correct.

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
26
A photon of wavelength 80 nm is absorbed by the electron in the ground-state level of the hydrogen atom. Is this enough energy to ionize the atom? If so calculate the kinetic energy of the free electron.
A) No, ionization does not occur.
B) Yes, 1.9 eV
C) Yes, 12 eV
D) Yes, 29 eV
E) Yes, 19 eV
A) No, ionization does not occur.
B) Yes, 1.9 eV
C) Yes, 12 eV
D) Yes, 29 eV
E) Yes, 19 eV

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
27
What is the energy difference between the transition with the longest wavelength in the Lyman series and the transition with the shortest wavelength in the Paschen series?
A) 10.2 eV
B) 8.7 eV
C) 4.9 eV
D) 11.7 eV
E) 12.1 eV
A) 10.2 eV
B) 8.7 eV
C) 4.9 eV
D) 11.7 eV
E) 12.1 eV

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
28
The energy of the nth level in a one-electron atom is En = -13.6(Z2/n2) eV. Consider a beryllium ion with all but one of its electrons removed (a beryllium atom normally has four electrons). What is the energy of the electron when it is in the third-lowest energy state?
A) -24 eV
B) -7.6 eV
C) -1.5 eV
D) 24 eV
E) 7.6 eV
A) -24 eV
B) -7.6 eV
C) -1.5 eV
D) 24 eV
E) 7.6 eV

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
29
What is the ratio of the radius of the n = 3 orbit to that of the n = 2 orbit?
A) 1.50
B) 4.50
C) 2.25
D) 0.666
E) None of these is correct.
A) 1.50
B) 4.50
C) 2.25
D) 0.666
E) None of these is correct.

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
30
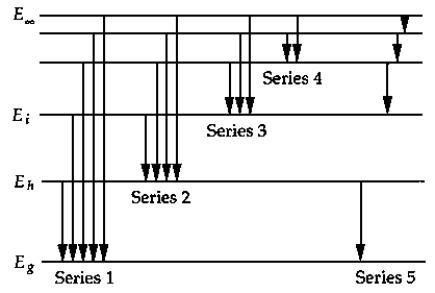 The above figure shows a schematic energy-level diagram for the hydrogen atom. The series that represents the Balmer series is
The above figure shows a schematic energy-level diagram for the hydrogen atom. The series that represents the Balmer series isA) 1
B) 2
C) 3
D) 4
E) 5

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
31
An electron in a hydrogen atom jumps from the n = 5 to n = 3 level. Is a photon absorbed or emitted in this process? What is the wavelength of the photon? State whether the photon is in the visible, ultraviolet, or infrared range of the electro-magnetic spectrum.
A) absorbed, 1280 nm, infrared
B) emitted, 605 nm, visible
C) emitted, 1280 nm, infrared
D) absorbed, 605 nm, visible
E) emitted, 605 nm, infrared
A) absorbed, 1280 nm, infrared
B) emitted, 605 nm, visible
C) emitted, 1280 nm, infrared
D) absorbed, 605 nm, visible
E) emitted, 605 nm, infrared

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
32
The energy of the nth level in a one-electron atom is En = -13.6(Z2/n2) eV. Consider a beryllium ion with all but one of its electrons removed (a beryllium atom normally has four electrons). What is the wavelength of a photon emitted when the electron makes the transition from the third-lowest to the lowest energy state?
A) 1.03 * 10-7 m
B) 2.03 * 10-8 m
C) 6.43 * 10-9 m
D) 5.71 * 10-9 m
E) 1.03 * 10-27 m
A) 1.03 * 10-7 m
B) 2.03 * 10-8 m
C) 6.43 * 10-9 m
D) 5.71 * 10-9 m
E) 1.03 * 10-27 m

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
33
The electron in a hydrogen atom has an orbital radius of 0.0500 nm. To avoid being pulled into the nucleus by electrostatic attraction, the electron must have an orbital speed of
A) 7.12 km/s
B) 25.2 km/s
C) 1.02 *106 m/s
D) 2.25 *106 m/s
E) 5.0 *108 m/s
A) 7.12 km/s
B) 25.2 km/s
C) 1.02 *106 m/s
D) 2.25 *106 m/s
E) 5.0 *108 m/s

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
34
An electron undergoes a transition from n = 2 to n = 5. According to Bohr's model, the change in angular momentum of the electron is
A)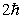
B)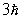
C)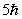
D)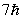
E) None of these is correct.
A)
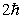
B)
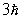
C)
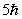
D)
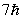
E) None of these is correct.

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
35
According to the Bohr theory, the allowed energy states for the hydrogen atom are given by the relation 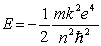 .
.
This formula can be readily extended to other hydrogenic (one-electron) systems. The energy of the second level (n = 2) for the doubly ionized lithium atom is
A) -54.4 eV
B) 13.6 eV
C) -30.6 eV
D) -3.4 eV
E) -1.5 eV
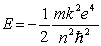 .
.This formula can be readily extended to other hydrogenic (one-electron) systems. The energy of the second level (n = 2) for the doubly ionized lithium atom is
A) -54.4 eV
B) 13.6 eV
C) -30.6 eV
D) -3.4 eV
E) -1.5 eV

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
36
The equation derived by Bohr for the wavelengths of of the lines in hydrogen- like spectra is 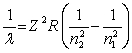 The first member of the Balmer series of hydrogen has = 660 nm. Doubly ionized
The first member of the Balmer series of hydrogen has = 660 nm. Doubly ionized 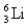 is hydrogen-like. The wavelength of the first member of the Balmer series for doubly ionized
is hydrogen-like. The wavelength of the first member of the Balmer series for doubly ionized 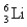 is
is
A) 73 nm
B) 5.9 * 103 nm
C) 150 nm
D) 60 nm
E) 1.8* 10-3 nm
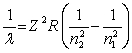 The first member of the Balmer series of hydrogen has = 660 nm. Doubly ionized
The first member of the Balmer series of hydrogen has = 660 nm. Doubly ionized 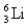 is hydrogen-like. The wavelength of the first member of the Balmer series for doubly ionized
is hydrogen-like. The wavelength of the first member of the Balmer series for doubly ionized 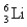 is
isA) 73 nm
B) 5.9 * 103 nm
C) 150 nm
D) 60 nm
E) 1.8* 10-3 nm

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
37
Light of wavelength 411 nm is observed from a hydrogen discharge. What transition produces this emission? The energy of the n = 1 level is -13.6 eV.
A) n = 1.13 to n =1
B) n = 6 to n = 2
C) n = 3 to n = 3
D) n = 2 to n = 6
E) n = 5 to n = 1
A) n = 1.13 to n =1
B) n = 6 to n = 2
C) n = 3 to n = 3
D) n = 2 to n = 6
E) n = 5 to n = 1

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
38
What is the energy difference between the transition with the longest wavelength and the transition with the shortest wavelength in the Balmer series?
A) 10.2 eV
B) 3.4 eV
C) 1.51 eV
D) 12.1 eV
E) 0.66 eV
A) 10.2 eV
B) 3.4 eV
C) 1.51 eV
D) 12.1 eV
E) 0.66 eV

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
39
According to Bohr's model, the radius of an electron at n = 4 is
A) 0.212 nm
B) 0.846 nm
C) 0.0265 nm
D) 0.00331 nm
E) None of these is correct.
A) 0.212 nm
B) 0.846 nm
C) 0.0265 nm
D) 0.00331 nm
E) None of these is correct.

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
40
The red line in the hydrogen emission spectrum is 656 nm. If the energy of the nth level is -13.6/n 2 eV, then calculate the transition between n levels that this emitted photon comes from.
A) n = 2 to n = 3
B) n = 4 to n = 3
C) n = 5 to n = 2
D) n = 3 to n = 2
E) n = 2 to n = 4
A) n = 2 to n = 3
B) n = 4 to n = 3
C) n = 5 to n = 2
D) n = 3 to n = 2
E) n = 2 to n = 4

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
41
In the Bohr Model of the hydrogen atom, what is the kinetic energy of the electron in the n = 3 orbit? (The radius of the 1st Bohr orbit is 0.0529 nm.)
A) 3.44 eV
B) 1.51 eV
C) 3.02 eV
D) 0.75 eV
E) 4.53 eV
A) 3.44 eV
B) 1.51 eV
C) 3.02 eV
D) 0.75 eV
E) 4.53 eV

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
42
A hydrogen atom is in a state with principal quantum number n = 3. A possible value for its orbital angular momentum is
A) zero
B)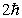
C)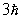
D)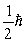
E)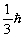
A) zero
B)
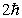
C)
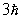
D)
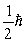
E)
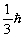

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
43
If you measure the angular momentum of an electron in units of 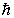 , you find that the angular momentum is quantized to the value _______ units and that its component along any direction can have only the _______ values ranging from -
, you find that the angular momentum is quantized to the value _______ units and that its component along any direction can have only the _______ values ranging from - 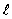 to +
to + 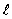 units.
units.
A)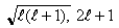
B)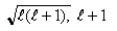
C)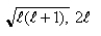
D)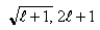
E)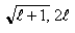
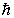 , you find that the angular momentum is quantized to the value _______ units and that its component along any direction can have only the _______ values ranging from -
, you find that the angular momentum is quantized to the value _______ units and that its component along any direction can have only the _______ values ranging from - 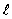 to +
to + 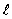 units.
units.A)
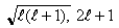
B)
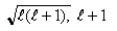
C)
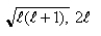
D)
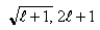
E)
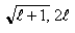

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
44
A possible value of the orbital angular momentum of an electron in the n = 2 state is
A)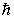
B)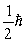
C)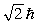
D)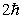
E)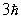
A)
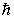
B)
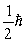
C)
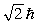
D)
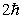
E)

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
45
Consider a beryllium (Z = 4) ion with all but one of its electrons removed. What is the kinetic energy of the electron in the n = 1 orbit. (The radius of the 1st Bohr orbit in Be3+ is 0.0132 nm.)
A) 54.4 eV
B) 218 eV
C) 13.6 eV
D) 27.2 eV
E) 109 eV
A) 54.4 eV
B) 218 eV
C) 13.6 eV
D) 27.2 eV
E) 109 eV

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
46
If the angular momentum is characterized by the quantum number 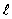 = 3, what is the smallest possible angle between
= 3, what is the smallest possible angle between 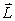 and the z axis?
and the z axis?
A) 12.1º
B) 17.5º
C) 23.2º
D) 27.4º
E) 30.0º
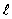 = 3, what is the smallest possible angle between
= 3, what is the smallest possible angle between 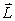 and the z axis?
and the z axis?A) 12.1º
B) 17.5º
C) 23.2º
D) 27.4º
E) 30.0º

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
47
For the principal quantum number n = 4, the number of values the orbital quantum number l can have is
A) 4
B) 3
C) 7
D) 16
E) 6
A) 4
B) 3
C) 7
D) 16
E) 6

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
48
If the angular momentum is characterized by the quantum number 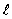 = 3, what is the largest possible angle between
= 3, what is the largest possible angle between 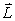 and the +z axis?
and the +z axis?
A) 30.0º
B) 60.8º
C) 81.4º
D) 150º
E) 163º
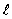 = 3, what is the largest possible angle between
= 3, what is the largest possible angle between 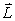 and the +z axis?
and the +z axis?A) 30.0º
B) 60.8º
C) 81.4º
D) 150º
E) 163º

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
49
The principle quantum number of an electron is 3. The possible magnitudes of the orbital angular momentum, L, are
A)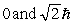
B)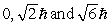
C)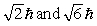
D)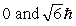
E) None of these is correct.
A)
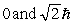
B)
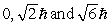
C)
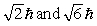
D)
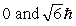
E) None of these is correct.

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
50
The possible orbital quantum numbers of an electron are 0, 1, 3, 4, and 5. Its principal quantum number, n, and the largest magnetic quantum number, ml are
A) 5 and 5
B) 6 and 5
C) 4 and 3
D) 6 and 4
E) 5 and 4
A) 5 and 5
B) 6 and 5
C) 4 and 3
D) 6 and 4
E) 5 and 4

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
51
In the Bohr Model of the hydrogen atom, what is the potential energy of the electron in the n = 11 orbit? (The radius of the 1st Bohr orbit is 0.0529 nm.)
A) 2.25 * 10-1 eV
B) 1.12*10-1 eV
C) 5.62 * 10-2 eV
D) 2.47 eV
E) None of these is correct.
A) 2.25 * 10-1 eV
B) 1.12*10-1 eV
C) 5.62 * 10-2 eV
D) 2.47 eV
E) None of these is correct.

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
52
What is the magnitude of the change in potential energy for the electron in the hydrogen atom as it moves from the n = 2 to n = 3 orbit? (The radius of the 1st Bohr orbit is 0.0529 nm.)
A) 1.89 eV
B) 4.91 eV
C) 0.945 eV
D) 3.78 eV
E) None of these is correct.
A) 1.89 eV
B) 4.91 eV
C) 0.945 eV
D) 3.78 eV
E) None of these is correct.

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
53
The symbol that represents the orbital quantum number is
A) n
B) m
C) L
D)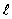
E) z
A) n
B) m
C) L
D)
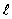
E) z

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
54
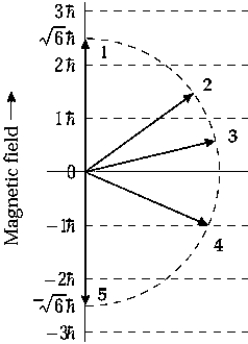 The orbital angular momentum of an electron in a D state has a magnitude of
The orbital angular momentum of an electron in a D state has a magnitude of 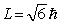 . The figure shows orientations of the angular momentum vector or an electron placed in a magnetic field in the positive z direction. The vector that represents a correct orientation when the field is applied is
. The figure shows orientations of the angular momentum vector or an electron placed in a magnetic field in the positive z direction. The vector that represents a correct orientation when the field is applied isA) 1
B) 2
C) 3
D) 4
E) 5

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
55
In the Bohr Model of the hydrogen atom, what is the ratio of the speed of the electron moving in the n = 2 orbit divided by the speed of the electron in the n = 3 orbit?
A) 0.66
B) 1.5
C) 2.25
D) 0.44
E) its speed is independent of n
A) 0.66
B) 1.5
C) 2.25
D) 0.44
E) its speed is independent of n

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
56
The symbol that represents the orbital angular momentum is
A) n
B) m
C) L
D)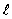
E) z
A) n
B) m
C) L
D)
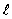
E) z

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
57
If the angular momentum is characterized by the quantum number 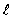 = 3, what are the possible values of Lz in units of
= 3, what are the possible values of Lz in units of 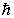 ?
?
A) -3, 0, +3
B) -3, -2, -1, 0
C) -2, -1, 0, +1, +2
D) -3, -2, -1, 0, +1, +2, +3
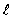 = 3, what are the possible values of Lz in units of
= 3, what are the possible values of Lz in units of 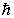 ?
?A) -3, 0, +3
B) -3, -2, -1, 0
C) -2, -1, 0, +1, +2
D) -3, -2, -1, 0, +1, +2, +3

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
58
The symbol that represents the principal quantum number is
A) n
B) m
C) L
D)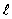
E) z
A) n
B) m
C) L
D)
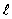
E) z

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
59
A hydrogen atom that has an electron with an orbital angular momentum 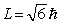 is placed in a magnetic field oriented in the z direction. The component of L in the z direction could be
is placed in a magnetic field oriented in the z direction. The component of L in the z direction could be
A)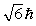
B)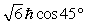
C)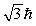
D)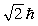
E)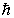
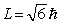 is placed in a magnetic field oriented in the z direction. The component of L in the z direction could be
is placed in a magnetic field oriented in the z direction. The component of L in the z direction could beA)
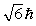
B)
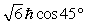
C)
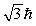
D)
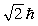
E)

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
60
The orbital angular momentum L is related to the orbital quantum number 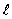 by
by
A)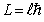
B)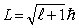
C)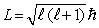
D)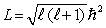
E)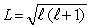
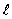 by
byA)
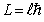
B)
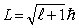
C)
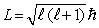
D)
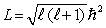
E)
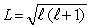

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
61
For the hydrogen atom in the state n = 2, l = 0, m = 0, the radial probability density is 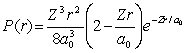 The probability of finding the electron in the range r = 0.04a0 at r = 1.5a0 is
The probability of finding the electron in the range r = 0.04a0 at r = 1.5a0 is
A) 0.00377
B) 0.00249
C) 0.00428
D) 0.0271
E) zero
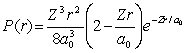 The probability of finding the electron in the range r = 0.04a0 at r = 1.5a0 is
The probability of finding the electron in the range r = 0.04a0 at r = 1.5a0 isA) 0.00377
B) 0.00249
C) 0.00428
D) 0.0271
E) zero

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
62
For the hydrogen atom in the ground state, the radial probability density is 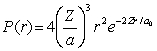 The probability of finding the electron in the range r = 0.04a0 at r = 2a0 is
The probability of finding the electron in the range r = 0.04a0 at r = 2a0 is
A) 0.0463
B) 0.0184
C) 0.0217
D) 0.0117
E) 0.0341
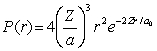 The probability of finding the electron in the range r = 0.04a0 at r = 2a0 is
The probability of finding the electron in the range r = 0.04a0 at r = 2a0 isA) 0.0463
B) 0.0184
C) 0.0217
D) 0.0117
E) 0.0341

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
63
 The set of quantum numbers for the probability density shown is
The set of quantum numbers for the probability density shown isA) n = 2,
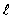 = 0, m = 0
= 0, m = 0B) n = 2,
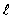 = 0, m = 1
= 0, m = 1C) n = 2,
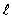 = 1, m = 0
= 1, m = 0D) n = 1,
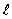 = 0, m = 0
= 0, m = 0E) n = 1,
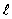 = 1, m = 0
= 1, m = 0
Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
64
For the hydrogen atom in the ground state, the wave function is 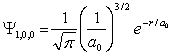 The probability of finding the electron from r = 0 to r = 2a0 is approximately
The probability of finding the electron from r = 0 to r = 2a0 is approximately
Note: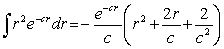
A) 6.34%
B) 12.7%
C) 18.0%
D) 32.3%
E) 76.2%
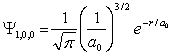 The probability of finding the electron from r = 0 to r = 2a0 is approximately
The probability of finding the electron from r = 0 to r = 2a0 is approximatelyNote:
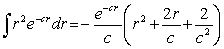
A) 6.34%
B) 12.7%
C) 18.0%
D) 32.3%
E) 76.2%

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
65
 The set of quantum numbers for the probability density shown is
The set of quantum numbers for the probability density shown isA) n = 2,
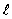 = 0, m = 0
= 0, m = 0B) n = 2,
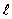 = 0, m = 2
= 0, m = 2C) n = 2,
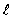 = 1, m= ±1
= 1, m= ±1D) n = 1,
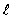 = 0, m = ±2
= 0, m = ±2E) n = 1,
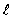 = 1, m = 0
= 1, m = 0
Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
66
Use the following figure for the next two problems. 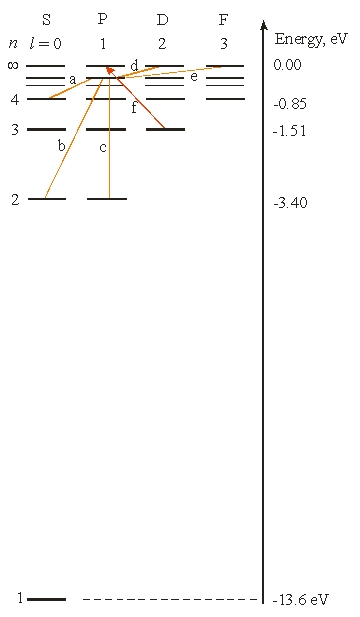
The energy of a hydrogen atom in the n = 5 state is approximately
A) -68 eV
B) -0.54 eV
C) +68 eV
D) +2.7 eV
E) +0.54 eV

The energy of a hydrogen atom in the n = 5 state is approximately
A) -68 eV
B) -0.54 eV
C) +68 eV
D) +2.7 eV
E) +0.54 eV

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
67
For the principal quantum number n = 4, the number of values the magnetic quantum number m can have is
A) 4
B) 3
C) 7
D) 16
E) 6
A) 4
B) 3
C) 7
D) 16
E) 6

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
68
A compact disc of a CD player has a moment of inertia I = 2.5 *10-5 kg · m2 and rotates at 500 rev/min. Taking L = I and using the quantization of angular momentum, the approximate value of L is ( 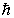 = 1.055* 10-34 J · s)
= 1.055* 10-34 J · s)
A) 1.2* 1032
B) 2.0 * 1030
C) 1.2* 1031
D) 130
E) 3.5 * 1015
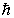 = 1.055* 10-34 J · s)
= 1.055* 10-34 J · s)A) 1.2* 1032
B) 2.0 * 1030
C) 1.2* 1031
D) 130
E) 3.5 * 1015

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
69
Use the following figure for the next two problems. 
What is the longest wavelength needed for an electron to make the transition labeled (f)?
A) 151 nm
B) 365 nm
C) 422 nm
D) 821 nm
E) 1459 nm

What is the longest wavelength needed for an electron to make the transition labeled (f)?
A) 151 nm
B) 365 nm
C) 422 nm
D) 821 nm
E) 1459 nm

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
70
The total number of distinct electron states (including spin) when n = 5 is
A) 18
B) 22
C) 25
D) 50
E) 72
A) 18
B) 22
C) 25
D) 50
E) 72

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
71
For the hydrogen atom in the ground state, the wave function is 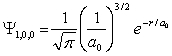 The probability of finding the electron from r = 0 to r = a0 is approximately
The probability of finding the electron from r = 0 to r = a0 is approximately
Note: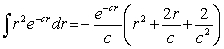
A) 6.34%
B) 12.7%
C) 18.0%
D) 32.3%
E) 76.2%
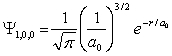 The probability of finding the electron from r = 0 to r = a0 is approximately
The probability of finding the electron from r = 0 to r = a0 is approximatelyNote:
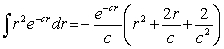
A) 6.34%
B) 12.7%
C) 18.0%
D) 32.3%
E) 76.2%

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
72
For the hydrogen atom in the ground state, the radial probability density is 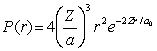 The probability of finding the electron in the range r = 0.04a0 at r = a0 is
The probability of finding the electron in the range r = 0.04a0 at r = a0 is
A) 0.0423
B) 0.0164
C) 0.0217
D) 0.0137
E) 0.0241
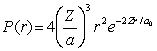 The probability of finding the electron in the range r = 0.04a0 at r = a0 is
The probability of finding the electron in the range r = 0.04a0 at r = a0 isA) 0.0423
B) 0.0164
C) 0.0217
D) 0.0137
E) 0.0241

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
73
For the hydrogen atom in the state n = 2, l = 0, m = 0, the radial probability density is 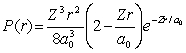 The probability of finding the electron in the range r = 0.04a0 at r = 2a0 is
The probability of finding the electron in the range r = 0.04a0 at r = 2a0 is
A) 0.0167
B) 0.149
C) 0.128
D) 0.0241
E) zero
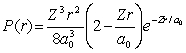 The probability of finding the electron in the range r = 0.04a0 at r = 2a0 is
The probability of finding the electron in the range r = 0.04a0 at r = 2a0 isA) 0.0167
B) 0.149
C) 0.128
D) 0.0241
E) zero

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
74
 The set of quantum numbers for the probability density shown is
The set of quantum numbers for the probability density shown isA) n = 2,
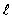 = 0, m = 0
= 0, m = 0B) n = 2,
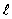 = 1, m = 0
= 1, m = 0C) n = 2,
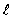 = 1, m = 1
= 1, m = 1D) n = 2,
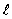 = 0, m = 1
= 0, m = 1E) n = 1,
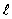 = 1, m = 0
= 1, m = 0
Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
75
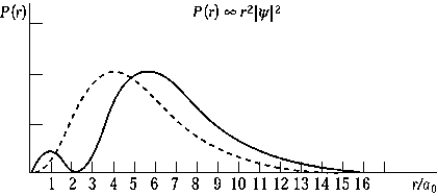 The dashed curve on the graph shows the probability of finding the electron at a distance r for
The dashed curve on the graph shows the probability of finding the electron at a distance r forA) n = 2,
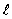 = 0
= 0B) n = 1,
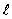 = 0
= 0C) n = 2,
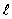 = 2
= 2D) n = 1,
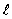 = 2
= 2E) n = 2,
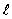 = 1
= 1
Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
76
For the hydrogen atom in the ground state, the radial probability density is 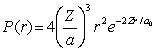 The probability of finding the electron in range r = 0.08a0 at r = 2a0 is approximately
The probability of finding the electron in range r = 0.08a0 at r = 2a0 is approximately
A) 2.34%
B) 3.67%
C) 5.86%
D) 6.25%
E) 7.43%
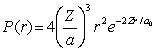 The probability of finding the electron in range r = 0.08a0 at r = 2a0 is approximately
The probability of finding the electron in range r = 0.08a0 at r = 2a0 is approximatelyA) 2.34%
B) 3.67%
C) 5.86%
D) 6.25%
E) 7.43%

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
77
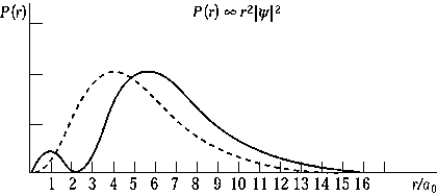 The solid curve on the graph shows the probability of finding the electron at a distance r for
The solid curve on the graph shows the probability of finding the electron at a distance r forA) n = 2,
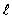 = 2
= 2B) n = 1,
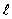 = 0
= 0C) n = 2,
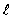 = 2
= 2D) n = 2,
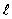 = 0
= 0E) n = 1,
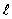 = 1
= 1
Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
78
Use the following figure for the next two problems. 
Which of the following transitions from (a) to (e) is(are) not allowed?
A) (a) and (b)
B) (d) and (e)
C) (c) and (e)
D) (c)
E) (d)

Which of the following transitions from (a) to (e) is(are) not allowed?
A) (a) and (b)
B) (d) and (e)
C) (c) and (e)
D) (c)
E) (d)

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
79
For the hydrogen atom in the ground state, the radial probability density is 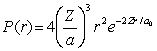 The probability of finding the electron in range r = 0.08a0 at r = a0 is approximately
The probability of finding the electron in range r = 0.08a0 at r = a0 is approximately
A) 3.24%
B) 4.33%
C) 5.87%
D) 6.25%
E) 7.43%
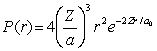 The probability of finding the electron in range r = 0.08a0 at r = a0 is approximately
The probability of finding the electron in range r = 0.08a0 at r = a0 is approximatelyA) 3.24%
B) 4.33%
C) 5.87%
D) 6.25%
E) 7.43%

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
80
An electron has a wave function given by 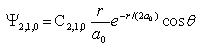 The probability of finding the electron when = 90 and = 0.5 10, and from r = a0 to 1.06a0 is approximately
The probability of finding the electron when = 90 and = 0.5 10, and from r = a0 to 1.06a0 is approximately
A) zero
B) 2.12%
C) 4.75%
D) 5.8%
E) 6.34%
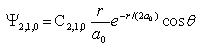 The probability of finding the electron when = 90 and = 0.5 10, and from r = a0 to 1.06a0 is approximately
The probability of finding the electron when = 90 and = 0.5 10, and from r = a0 to 1.06a0 is approximatelyA) zero
B) 2.12%
C) 4.75%
D) 5.8%
E) 6.34%

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck


