Deck 17: Mathematical Problems and Solutions
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/48
Play
Full screen (f)
Deck 17: Mathematical Problems and Solutions
1
The solution of 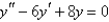 is
is
A)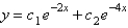
B)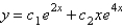
C)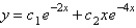
D)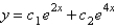
E)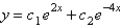
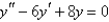 is
isA)
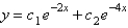
B)
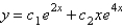
C)
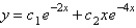
D)
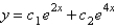
E)
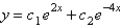
D
2
The solution of 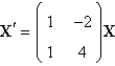 is
is
A)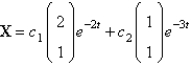
B)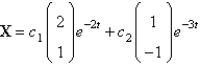
C)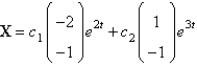
D)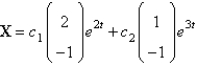
E)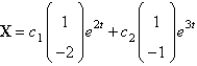
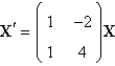 is
isA)
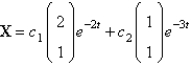
B)
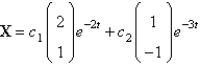
C)
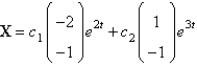
D)
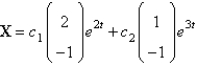
E)
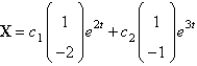
D
3
Using the convolution theorem, we find that 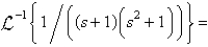
A)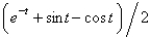
B)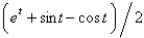
C)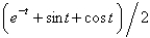
D)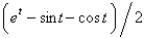
E)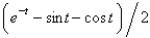
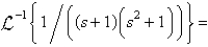
A)
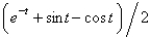
B)
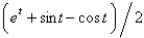
C)
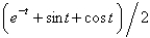
D)
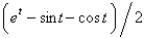
E)
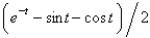
A
4
Using power series methods, the solution of 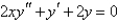 is
is
A)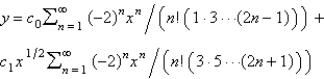
B)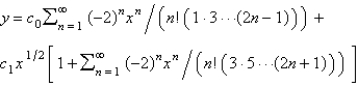
C)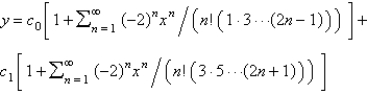
D)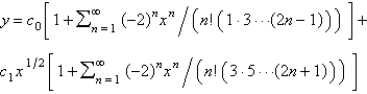
E)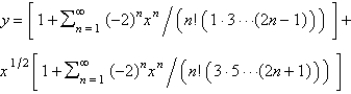
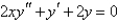 is
isA)
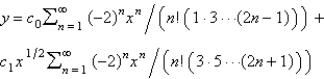
B)
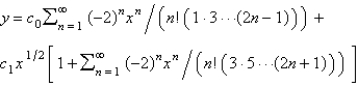
C)
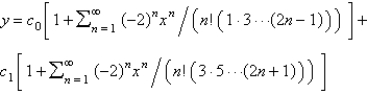
D)
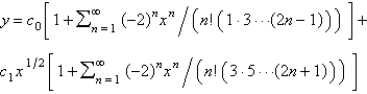
E)
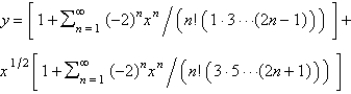

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
5
The solution of 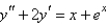 is
is
A)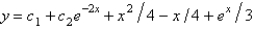
B)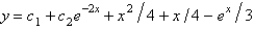
C)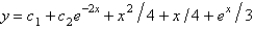
D)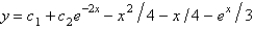
E)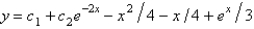
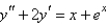 is
isA)
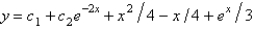
B)
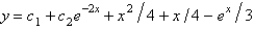
C)
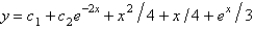
D)
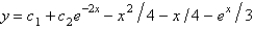
E)
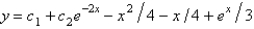

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
6
The solution of 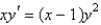 is
is
A)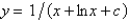
B)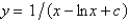
C)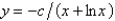
D)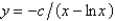
E)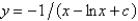
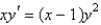 is
isA)
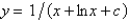
B)
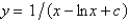
C)
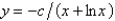
D)
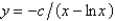
E)
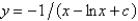

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
7
In the previous problem, the solution for the temperature is
A)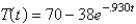
B)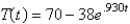
C)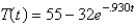
D)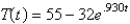
E)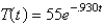
A)
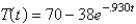
B)
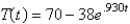
C)
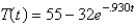
D)
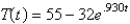
E)
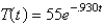

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
8
The solution of 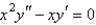 is
is
A)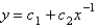
B)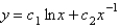
C)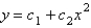
D)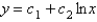
E)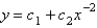
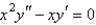 is
isA)
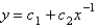
B)
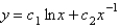
C)
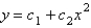
D)
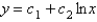
E)
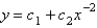

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
9
Using Laplace transform methods, the solution of 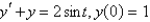 is (Hint: the previous problem might be useful.)
is (Hint: the previous problem might be useful.)
A)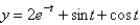
B)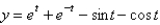
C)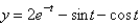
D)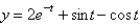
E)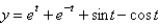
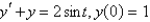 is (Hint: the previous problem might be useful.)
is (Hint: the previous problem might be useful.)A)
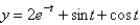
B)
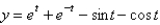
C)
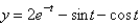
D)
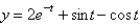
E)
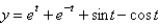

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
10
In the previous problem, the solution for the position, 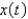 , is
, is
A)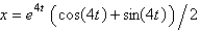
B)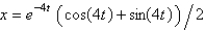
C)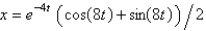
D)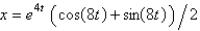
E)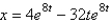
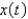 , is
, isA)
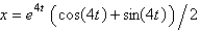
B)
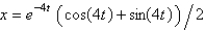
C)
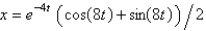
D)
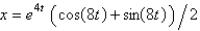
E)
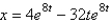

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
11
Using Laplace transform methods, the solution of 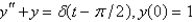 ,
, 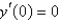 is
is
A)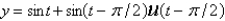
B)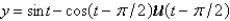
C)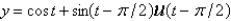
D)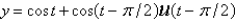
E)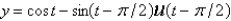
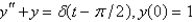 ,
, 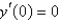 is
isA)
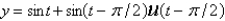
B)
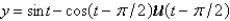
C)
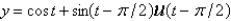
D)
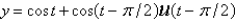
E)
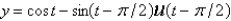

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
12
The solution of 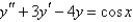 is
is
A)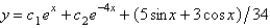
B)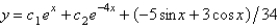
C)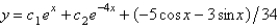
D)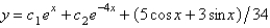
E)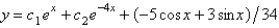
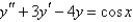 is
isA)
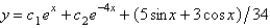
B)
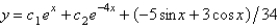
C)
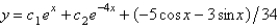
D)
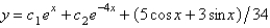
E)
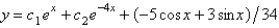

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
13
The solution of 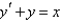 is
is
A)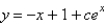
B)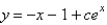
C)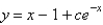
D)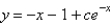
E)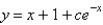
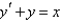 is
isA)
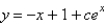
B)
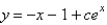
C)
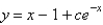
D)
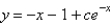
E)
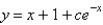

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
14
A 4-pound weight is hung on a spring and stretches it 1 foot. The mass spring system is then put into motion in a medium offering a damping force numerically equal to the velocity. If the mass is pulled down 6 inches from equilibrium and released, the initial value problem describing the position, 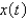 , of the mass at time t is
, of the mass at time t is
A)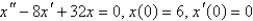
B)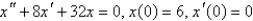
C)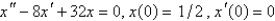
D)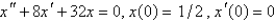
E)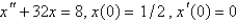
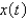 , of the mass at time t is
, of the mass at time t isA)
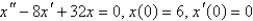
B)
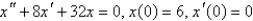
C)
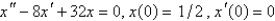
D)
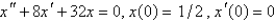
E)
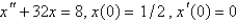

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
15
The solution of 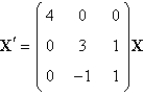 are
are
A)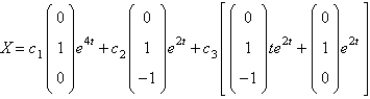
B)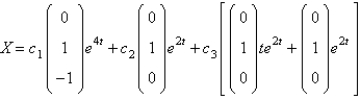
C)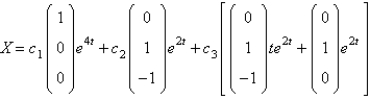
D)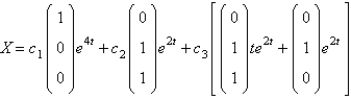
E)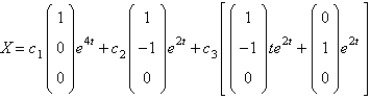
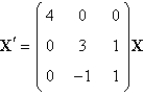 are
areA)
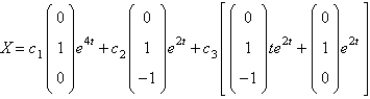
B)

C)
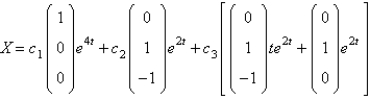
D)
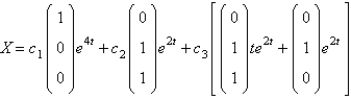
E)
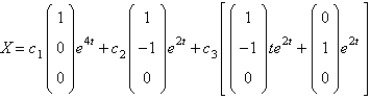

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
16
The solution of 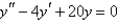 is
is
A)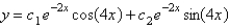
B)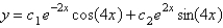
C)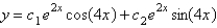
D)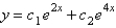
E)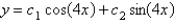
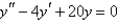 is
isA)
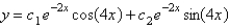
B)
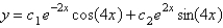
C)
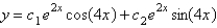
D)
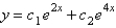
E)
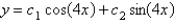

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
17
Using power series methods, the solution of 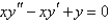 is
is
A)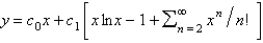
B)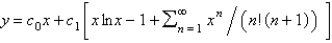
C)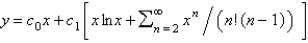
D)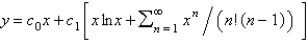
E)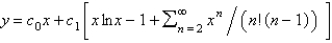
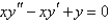 is
isA)
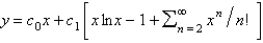
B)
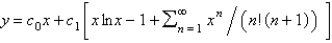
C)
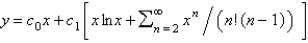
D)
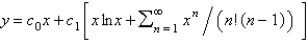
E)
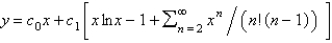

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
18
A frozen chicken at 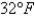 is taken out of the freezer and placed on a table at
is taken out of the freezer and placed on a table at 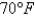 . One hour later the temperature of the chicken is
. One hour later the temperature of the chicken is 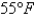 . The mathematical model for the temperature
. The mathematical model for the temperature 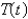 as a function of time
as a function of time 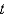 is (assuming Newton 's law of warming)
is (assuming Newton 's law of warming)
A)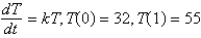
B)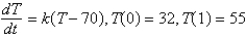
C)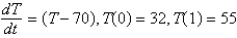
D)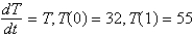
E)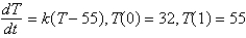
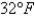 is taken out of the freezer and placed on a table at
is taken out of the freezer and placed on a table at 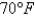 . One hour later the temperature of the chicken is
. One hour later the temperature of the chicken is 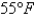 . The mathematical model for the temperature
. The mathematical model for the temperature 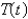 as a function of time
as a function of time 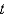 is (assuming Newton 's law of warming)
is (assuming Newton 's law of warming)A)
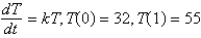
B)
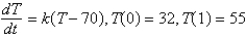
C)
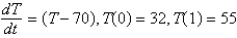
D)
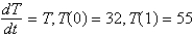
E)
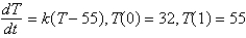

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
19
The solution of 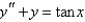 is
is
A)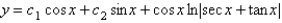
B)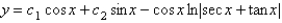
C)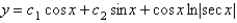
D)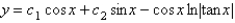
E)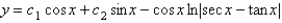
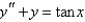 is
isA)
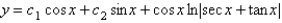
B)
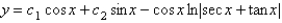
C)
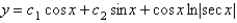
D)
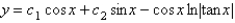
E)
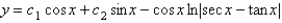

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
20
The correct form of the particular solution of 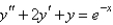 is
is
A)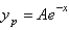
B)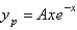
C)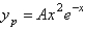
D)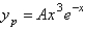
E) none of the above
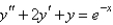 is
isA)
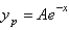
B)
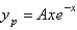
C)
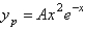
D)
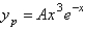
E) none of the above

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
21
In the previous two problems, the error in the improved Euler method at 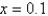 is
is
A)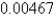
B) 0.000165
C) 0.870
D) 0.895
E) 0.0897
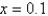 is
isA)
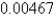
B) 0.000165
C) 0.870
D) 0.895
E) 0.0897

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
22
Consider the problem 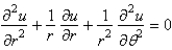 with boundary conditions
with boundary conditions 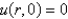 ,
, 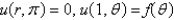 . Separate variables using
. Separate variables using 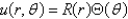 . The resulting problems for
. The resulting problems for 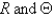 are
are
A)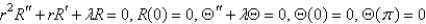
B)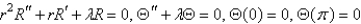
C)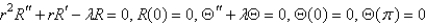
D)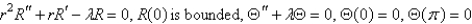
E)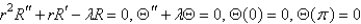
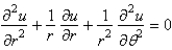 with boundary conditions
with boundary conditions 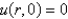 ,
, 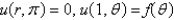 . Separate variables using
. Separate variables using 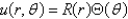 . The resulting problems for
. The resulting problems for 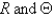 are
areA)
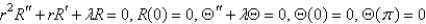
B)
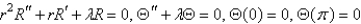
C)
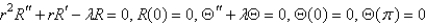
D)
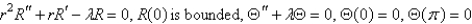
E)
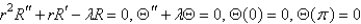

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
23
The solutions of the eigenvalue problem and the other problem from the previous problem are
A)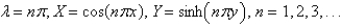
B)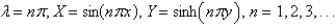
C)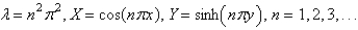
D)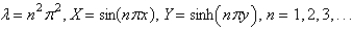
E)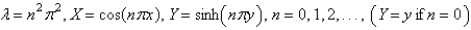
A)
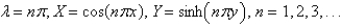
B)
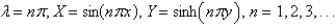
C)
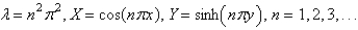
D)
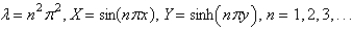
E)
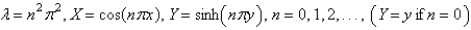

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
24
In the previous problem, the error in the classical Runge-Kutta method at 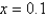 is (Hint: see the previous five problems.)
is (Hint: see the previous five problems.)
A) 0.00083
B) 0.000083
C) 0.000000083
D) 0.0000083
E) 0.00000083
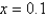 is (Hint: see the previous five problems.)
is (Hint: see the previous five problems.)A) 0.00083
B) 0.000083
C) 0.000000083
D) 0.0000083
E) 0.00000083

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
25
In the previous problem, the solution for 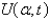 is
is
A)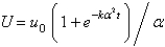
B)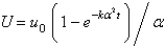
C)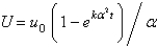
D)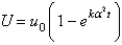
E)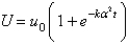
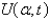 is
isA)
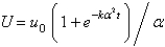
B)
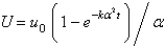
C)
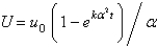
D)
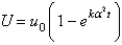
E)
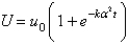

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
26
The solution of 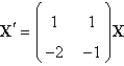 is
is
A)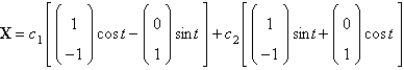
B)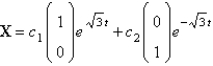
C)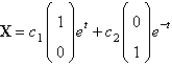
D)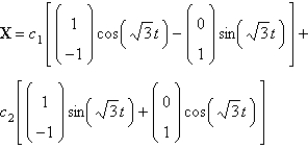
E)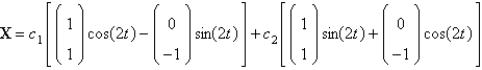
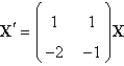 is
isA)
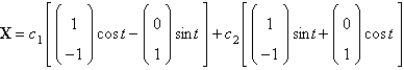
B)
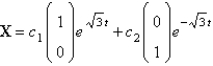
C)
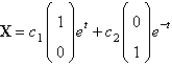
D)
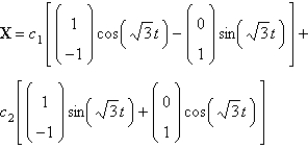
E)
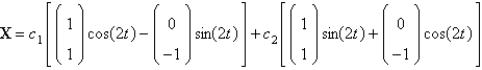

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
27
Consider the non-linear system 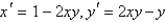 . The linearized system about the one critical point,
. The linearized system about the one critical point, 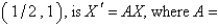
A)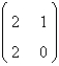
B)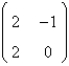
C)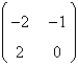
D)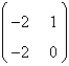
E)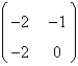
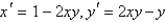 . The linearized system about the one critical point,
. The linearized system about the one critical point, 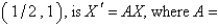
A)

B)

C)
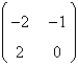
D)
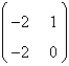
E)
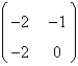

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
28
Consider the heat problem 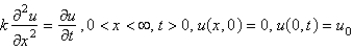 . Apply a Fourier sine transform. The resulting problem for
. Apply a Fourier sine transform. The resulting problem for 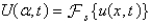 is
is
A)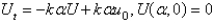
B)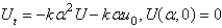
C)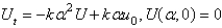
D)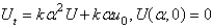
E)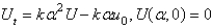
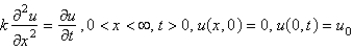 . Apply a Fourier sine transform. The resulting problem for
. Apply a Fourier sine transform. The resulting problem for 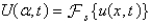 is
isA)
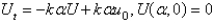
B)
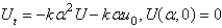
C)
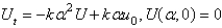
D)
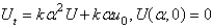
E)
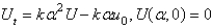

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
29
Let 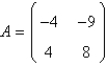 , and consider the system
, and consider the system 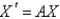 . The critical point
. The critical point 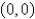 of the system is a
of the system is a
A) stable node
B) unstable node
C) unstable saddle
D) stable spiral point
E) unstable spiral point
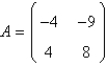 , and consider the system
, and consider the system 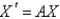 . The critical point
. The critical point 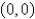 of the system is a
of the system is aA) stable node
B) unstable node
C) unstable saddle
D) stable spiral point
E) unstable spiral point

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
30
Consider Laplace's equation on a rectangle, 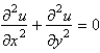 with boundary conditions
with boundary conditions 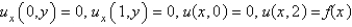 . When the variables are separated using
. When the variables are separated using 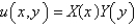 , the resulting problems for
, the resulting problems for 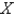 and
and 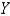 are
are
A)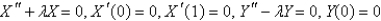
B)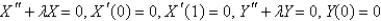
C)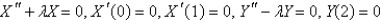
D)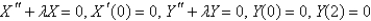
E)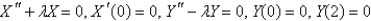
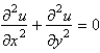 with boundary conditions
with boundary conditions 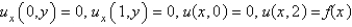 . When the variables are separated using
. When the variables are separated using 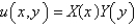 , the resulting problems for
, the resulting problems for 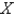 and
and 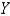 are
areA)
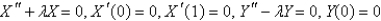
B)
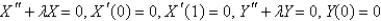
C)
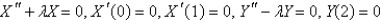
D)
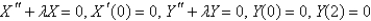
E)
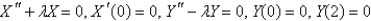

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
31
Using the improved Euler method with a step size of 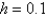 , the solution of
, the solution of 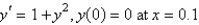 is
is
A)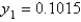
B)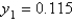
C)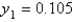
D)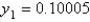
E)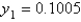
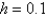 , the solution of
, the solution of 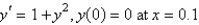 is
isA)
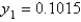
B)
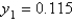
C)
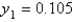
D)
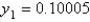
E)
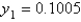

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
32
The solution of the eigenvalue problem 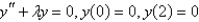 is
is
A)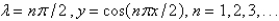
B)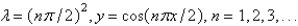
C)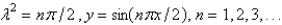
D)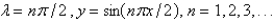
E)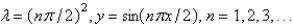
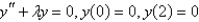 is
isA)
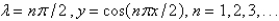
B)
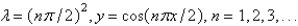
C)
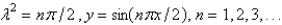
D)
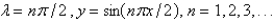
E)
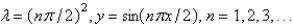

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
33
In the previous problem, the exact solution of the initial value problem is
A)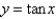
B)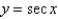
C)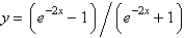
D)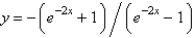
E)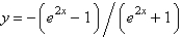
A)
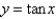
B)
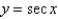
C)
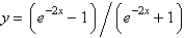
D)
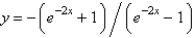
E)
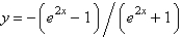

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
34
In the previous problem, for both the linearized system and the non-linear system, the critical point is a
A) unstable node
B) stable node
C) saddle point
D) unstable spiral point
E) stable spiral point
A) unstable node
B) stable node
C) saddle point
D) unstable spiral point
E) stable spiral point

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
35
In the previous two problems, the solution for 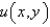 is
is
A)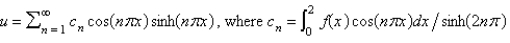
B)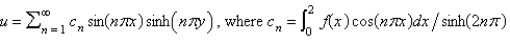
C)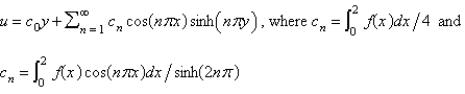
D)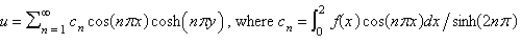
E)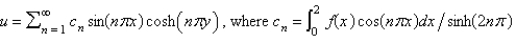
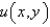 is
isA)
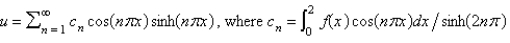
B)
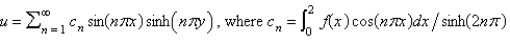
C)
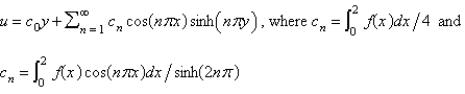
D)
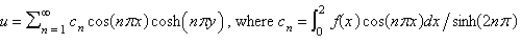
E)
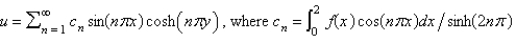

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
36
A particular solution of 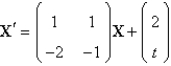 is
is
A)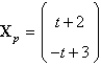
B)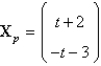
C)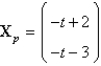
D)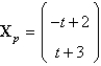
E)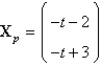
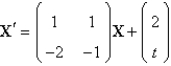 is
isA)
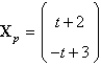
B)
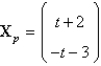
C)
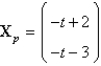
D)
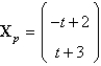
E)
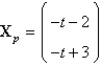

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
37
Let 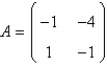 , and consider the system
, and consider the system 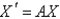 . The critical point
. The critical point 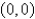 of the system is a spiral point. The origin is
of the system is a spiral point. The origin is
A) unstable, and the solutions recede from the origin clockwise as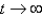 .
.
B) unstable, and the solutions recede from the origin counter-clockwise as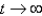 .
.
C) stable, and the solutions approach the origin clockwise as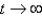 .
.
D) stable, and the solutions approach the origin counter-clockwise as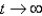 .
.
E) none of the above
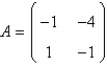 , and consider the system
, and consider the system 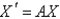 . The critical point
. The critical point 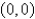 of the system is a spiral point. The origin is
of the system is a spiral point. The origin isA) unstable, and the solutions recede from the origin clockwise as
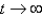 .
.B) unstable, and the solutions recede from the origin counter-clockwise as
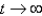 .
.C) stable, and the solutions approach the origin clockwise as
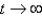 .
.D) stable, and the solutions approach the origin counter-clockwise as
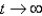 .
.E) none of the above

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
38
In the previous two problems, the infinite series solution for 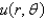 is
is 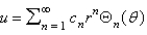 , where
, where 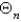 is found in the previous problem, and
is found in the previous problem, and
A)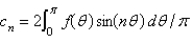
B)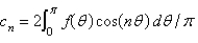
C)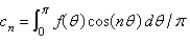
D)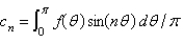
E)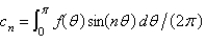
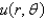 is
is 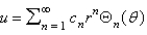 , where
, where 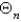 is found in the previous problem, and
is found in the previous problem, andA)
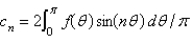
B)
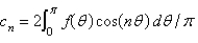
C)
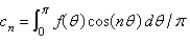
D)
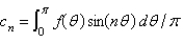
E)
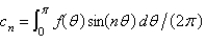

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
39
The solutions for 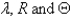 from the previous problem are
from the previous problem are
A)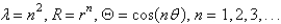
B)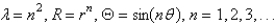
C)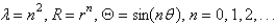
D)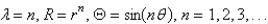
E)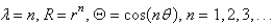
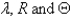 from the previous problem are
from the previous problem areA)
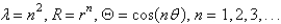
B)
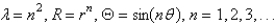
C)
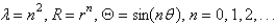
D)
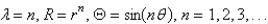
E)
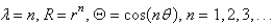

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
40
Using the classical Runge-Kutta method of order 4 with a step size of 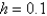 , the solution of
, the solution of 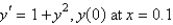 is
is
A) 0.099589
B) 0.100334589
C) 0.10034589
D) 0.10334589
E) 0.1034589
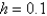 , the solution of
, the solution of 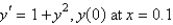 is
isA) 0.099589
B) 0.100334589
C) 0.10034589
D) 0.10334589
E) 0.1034589

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
41
In the previous two problems, the solution for u along the line 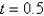 at the mesh points is Select all that apply.
at the mesh points is Select all that apply.
A)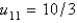
B)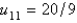
C)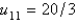
D)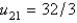
E)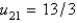
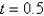 at the mesh points is Select all that apply.
at the mesh points is Select all that apply.A)
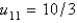
B)
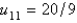
C)
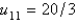
D)
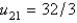
E)
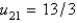

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
42
In the previous problem, using the notation 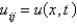 , and letting
, and letting 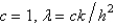 , the equation becomes
, the equation becomes
A)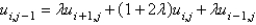
B)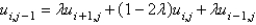
C)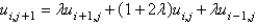
D)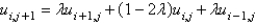
E)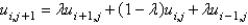
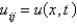 , and letting
, and letting 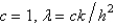 , the equation becomes
, the equation becomesA)
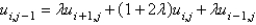
B)
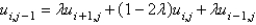
C)
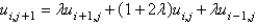
D)
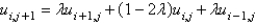
E)
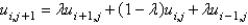

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
43
Is the value of 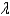 in the previous problem such that the scheme is stable?
in the previous problem such that the scheme is stable?
A) yes
B) no
C) It is right on the borderline.
D) It cannot be determined from the available data.
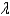 in the previous problem such that the scheme is stable?
in the previous problem such that the scheme is stable?A) yes
B) no
C) It is right on the borderline.
D) It cannot be determined from the available data.

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
44
The Fourier series of an even function can contain Select all that apply.
A) sine terms
B) cosine terms
C) a constant term
D) more than one of the above
E) none of the above
A) sine terms
B) cosine terms
C) a constant term
D) more than one of the above
E) none of the above

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
45
The eigenvalue-eigenvector pairs for the matrix 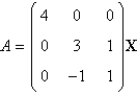 are Select all that apply.
are Select all that apply.
A)
B)
C)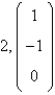
D)
E)
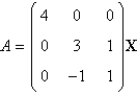 are Select all that apply.
are Select all that apply.A)

B)

C)

D)

E)


Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
46
In the previous two problem, the solution for 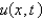 is
is
A)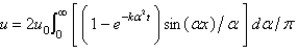
B)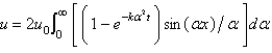
C)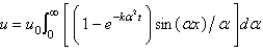
D)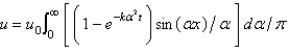
E)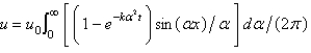
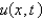 is
isA)
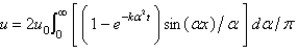
B)
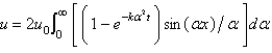
C)
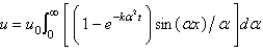
D)
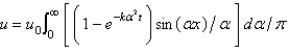
E)
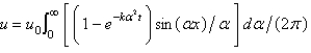

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
47
The solutions of a regular Sturm-Liouville problem 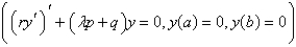 have which of the following properties?
have which of the following properties?
A) There exists an infinite number of real eigenvalues.
B) The eigenvalues are orthogonal on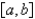 .
.
C) For each eigenvalue, there is only one eigenfunction (except for non-zero constant multiples).
D) Eigenfunctions corresponding to different eigenvalues are linearly independent.
E) The set of eigenfunctions corresponding to the set of eigenvalues is orthogonal with respect to the weight function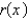 on the interval
on the interval 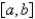 .
.
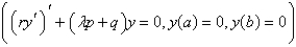 have which of the following properties?
have which of the following properties?A) There exists an infinite number of real eigenvalues.
B) The eigenvalues are orthogonal on
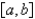 .
.C) For each eigenvalue, there is only one eigenfunction (except for non-zero constant multiples).
D) Eigenfunctions corresponding to different eigenvalues are linearly independent.
E) The set of eigenfunctions corresponding to the set of eigenvalues is orthogonal with respect to the weight function
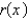 on the interval
on the interval 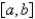 .
.
Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
48
Consider the heat problem 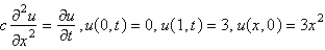 . Replace
. Replace 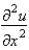 with a central difference approximation with
with a central difference approximation with 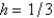 and
and 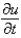 with a forward difference approximation with
with a forward difference approximation with 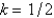 . The resulting equation is
. The resulting equation is
A)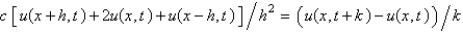
B)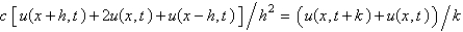
C)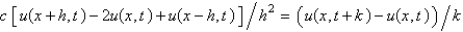
D)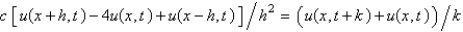
E)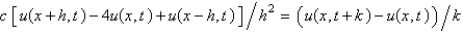
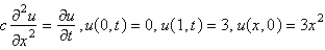 . Replace
. Replace 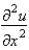 with a central difference approximation with
with a central difference approximation with 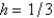 and
and 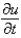 with a forward difference approximation with
with a forward difference approximation with 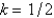 . The resulting equation is
. The resulting equation isA)
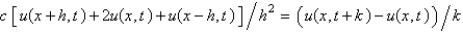
B)
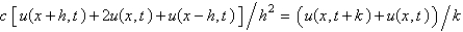
C)
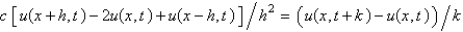
D)
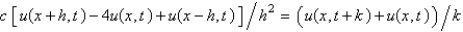
E)
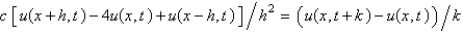

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck


