Deck 12: Boundary-Value Problems in Rectangular Coordinates
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/40
Play
Full screen (f)
Deck 12: Boundary-Value Problems in Rectangular Coordinates
1
The general solution of 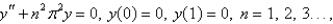 is
is
A)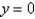
B)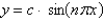
C)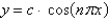
D)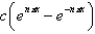
E)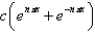
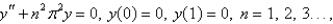 is
isA)
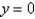
B)
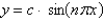
C)
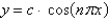
D)
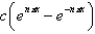
E)
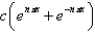
B
2
The solution of the eigenvalue problem from the previous problem is
A)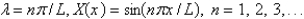
B)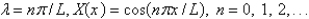
C)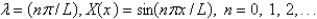
D)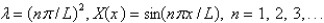
E)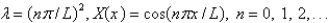
A)
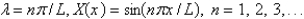
B)
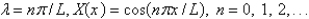
C)
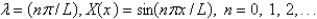
D)
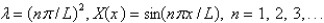
E)
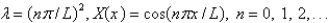
E
3
The wave equation for a vibrating string is derived using the assumptions Select all that apply.
A) the string is perfectly flexible.
B) the displacements may be large.
C) the tension acts perpendicular to the string.
D) the tension is large compared with gravity.
E) the string is homogeneous.
A) the string is perfectly flexible.
B) the displacements may be large.
C) the tension acts perpendicular to the string.
D) the tension is large compared with gravity.
E) the string is homogeneous.
A, D, E
4
The differential equation 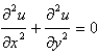 is
is
A) first order, linear, homogeneous
B) first order, linear, non-homogeneous
C) second order, nonlinear
D) second order, linear, homogeneous
E) second order, linear, non-homogeneous
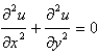 is
isA) first order, linear, homogeneous
B) first order, linear, non-homogeneous
C) second order, nonlinear
D) second order, linear, homogeneous
E) second order, linear, non-homogeneous

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
5
The differential equation 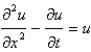 is Select all that apply.
is Select all that apply.
A) nonlinear
B) linear
C) hyperbolic
D) elliptic
E) parabolic
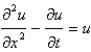 is Select all that apply.
is Select all that apply.A) nonlinear
B) linear
C) hyperbolic
D) elliptic
E) parabolic

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
6
In the previous three problems, the solution of the original problem is
A)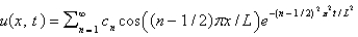 , where
, where 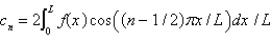
B)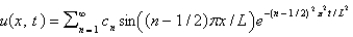 , where
, where 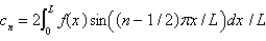
C)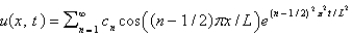 , where
, where 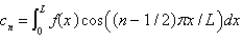
D)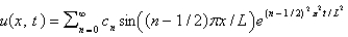 , where
, where 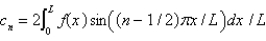
E)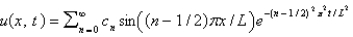 , where
, where 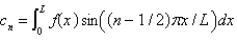
A)
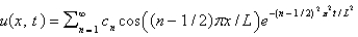 , where
, where 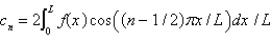
B)
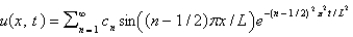 , where
, where 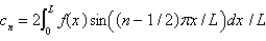
C)
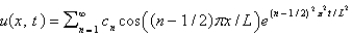 , where
, where 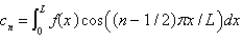
D)
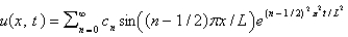 , where
, where 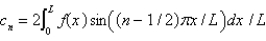
E)
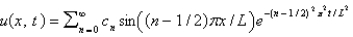 , where
, where 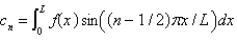

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
7
The solution of the eigenvalue problem from the previous problem is
A)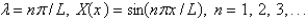
B)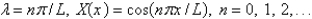
C)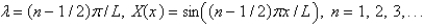
D)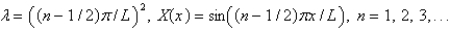
E)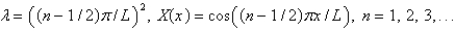
A)
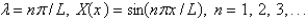
B)
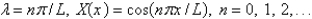
C)
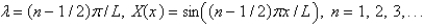
D)
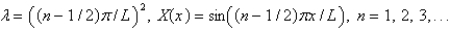
E)
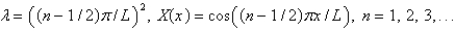

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
8
In the previous three problems, the solution of the original problem is
A)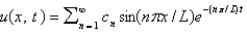 , where
, where 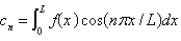
B)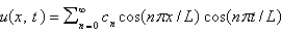 , where
, where 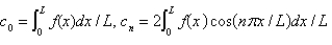
C)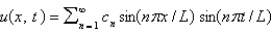 , where
, where 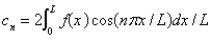
D)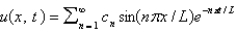 , where
, where 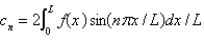
E)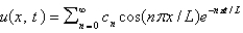 , where
, where 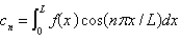
A)
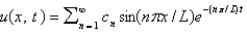 , where
, where 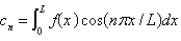
B)
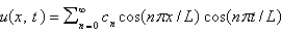 , where
, where 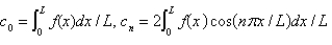
C)
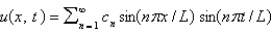 , where
, where 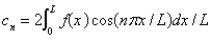
D)
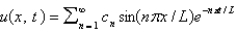 , where
, where 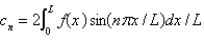
E)
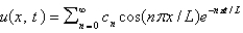 , where
, where 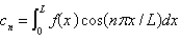

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
9
The differential equation 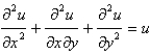 is Select all that apply.
is Select all that apply.
A) linear
B) nonlinear
C) hyperbolic
D) elliptic
E) parabolic
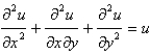 is Select all that apply.
is Select all that apply.A) linear
B) nonlinear
C) hyperbolic
D) elliptic
E) parabolic

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
10
Consider the equation 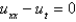 with conditions
with conditions 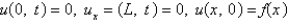 . When separating variables with
. When separating variables with 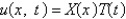 , the resulting problems for
, the resulting problems for 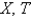 are
are
A)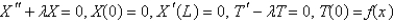
B)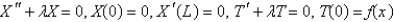
C)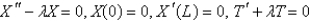
D)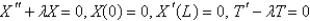
E)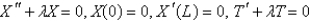
 with conditions
with conditions 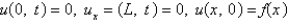 . When separating variables with
. When separating variables with 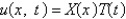 , the resulting problems for
, the resulting problems for 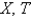 are
areA)
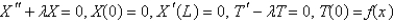
B)
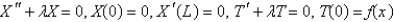
C)
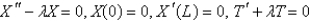
D)
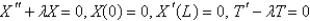
E)
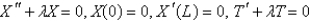

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
11
Consider the equation 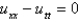 with conditions
with conditions 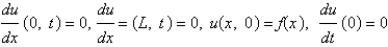 . When separating variables with
. When separating variables with 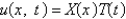 , the resulting problems for
, the resulting problems for 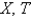 are
are
A)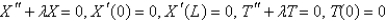
B)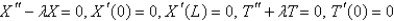
C)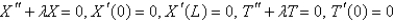
D)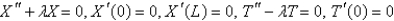
E)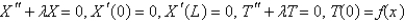
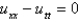 with conditions
with conditions 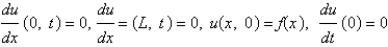 . When separating variables with
. When separating variables with 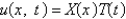 , the resulting problems for
, the resulting problems for 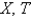 are
areA)
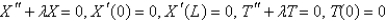
B)
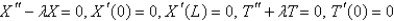
C)
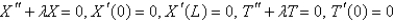
D)
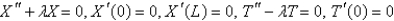
E)
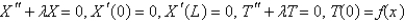

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
12
In the previous two problems, the product solutions are
A)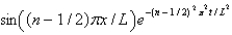
B)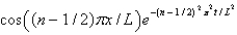
C)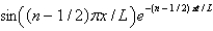
D)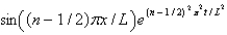
E)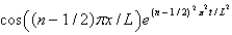
A)
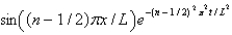
B)
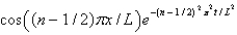
C)
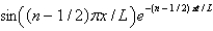
D)
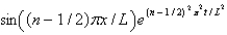
E)
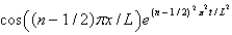

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
13
The solution of the previous three problems is 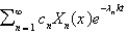 , where
, where 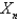 and
and 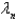 are given in the previous problem and
are given in the previous problem and
A)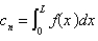
B)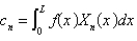
C)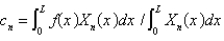
D)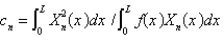
E)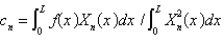
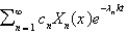 , where
, where 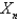 and
and 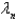 are given in the previous problem and
are given in the previous problem andA)
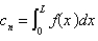
B)
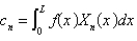
C)
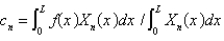
D)
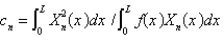
E)
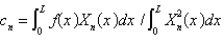

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
14
After separating variables in the previous problem, the eigenvalue problem becomes
A)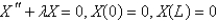
B)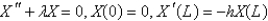
C)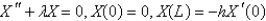
D)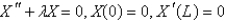
E)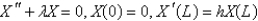
A)
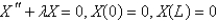
B)
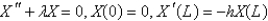
C)
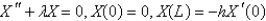
D)
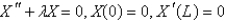
E)
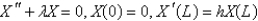

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
15
In the previous two problems, the product solutions are
A)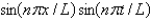
B)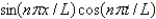
C)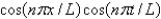
D)
E)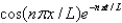
A)
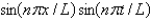
B)
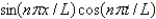
C)
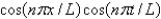
D)

E)
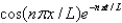

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
16
The solution of 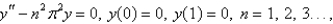 is
is
A)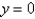
B)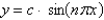
C)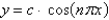
D)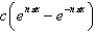
E)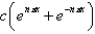
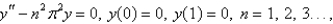 is
isA)
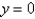
B)
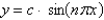
C)
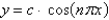
D)
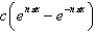
E)
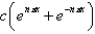

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
17
When 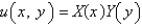 is substituted into the equation
is substituted into the equation 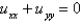 , the resulting equations for
, the resulting equations for 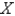 and
and 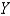 are
are
A)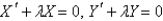
B)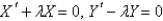
C)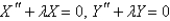
D)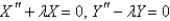
E)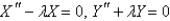
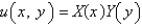 is substituted into the equation
is substituted into the equation 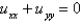 , the resulting equations for
, the resulting equations for 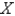 and
and 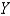 are
areA)
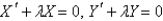
B)
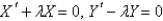
C)
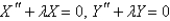
D)
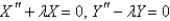
E)
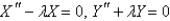

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
18
The solution of the eigenvalue problem in the previous problem is
A)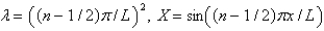
B)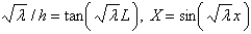
C)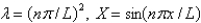
D)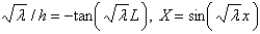
E)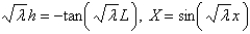
A)
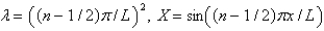
B)
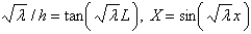
C)
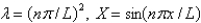
D)
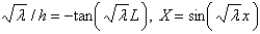
E)
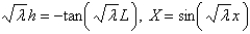

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
19
The solution of 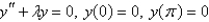 if
if 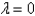 is
is
A)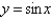
B)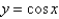
C)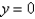
D)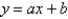
E)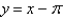
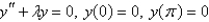 if
if 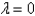 is
isA)
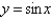
B)
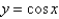
C)
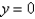
D)
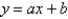
E)
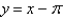

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
20
The model describing the temperature in a rod where the temperature at the left end is zero and where there is heat transfer from the right boundary into the external medium is
A)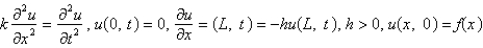
B)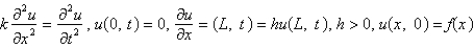
C)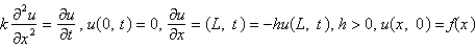
D)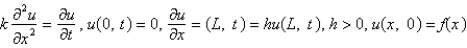
E)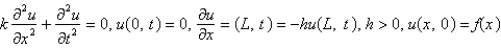
A)
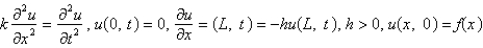
B)
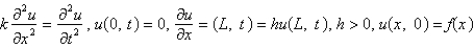
C)
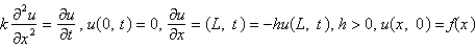
D)
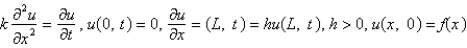
E)
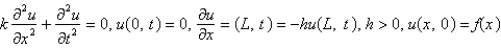

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
21
Consider the equation 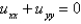 with conditions
with conditions 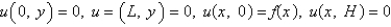 . When separating variables with
. When separating variables with 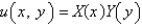 , the resulting problems for
, the resulting problems for 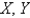 are
are
A)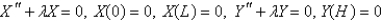
B)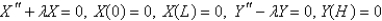
C)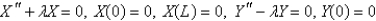
D)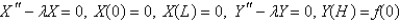
E)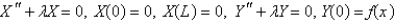
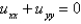 with conditions
with conditions 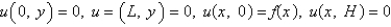 . When separating variables with
. When separating variables with 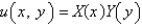 , the resulting problems for
, the resulting problems for 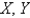 are
areA)
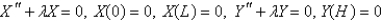
B)
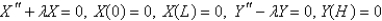
C)
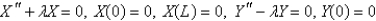
D)
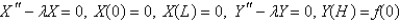
E)
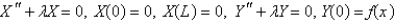

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
22
In the previous problem, the eigenfunction expansion if 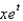 is
is
A)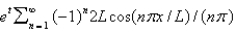
B)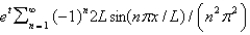
C)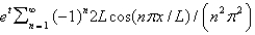
D)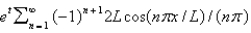
E)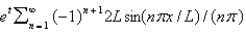
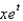 is
isA)
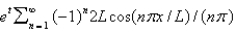
B)
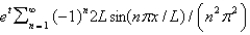
C)
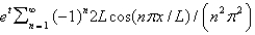
D)
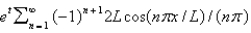
E)
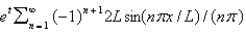

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
23
When 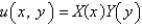 is substituted into the equation
is substituted into the equation 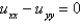 , the resulting equations for
, the resulting equations for 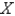 and
and 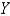 are
are
A)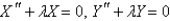
B)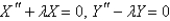
C)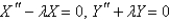
D)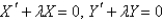
E)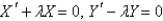
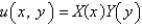 is substituted into the equation
is substituted into the equation 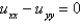 , the resulting equations for
, the resulting equations for 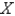 and
and 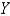 are
areA)
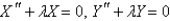
B)
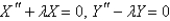
C)
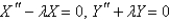
D)
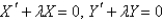
E)
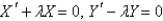

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
24
The solution of the eigenvalue problem from the previous problem is
A)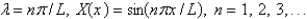
B)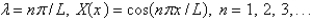
C)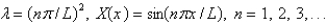
D)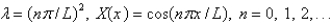
E)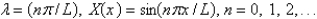
A)
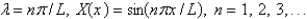
B)
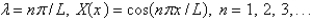
C)
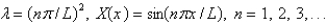
D)
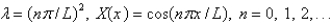
E)
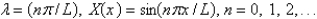

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
25
The solution of the eigenvalue problem from the previous problem is
A)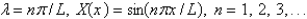
B)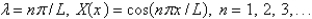
C)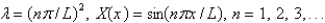
D)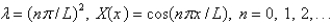
E)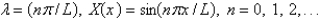
A)
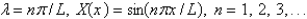
B)
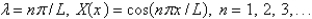
C)
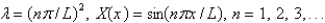
D)
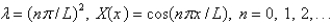
E)
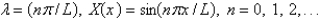

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
26
The solution of 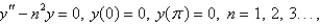 is
is
A)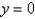
B)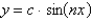
C)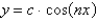
D)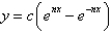
E)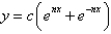
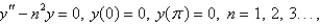 is
isA)
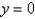
B)
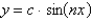
C)
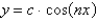
D)
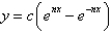
E)
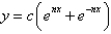

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
27
The differential equation 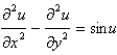 is Select all that apply.
is Select all that apply.
A) linear
B) nonlinear
C) hyperbolic
D) elliptic
E) parabolic
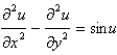 is Select all that apply.
is Select all that apply.A) linear
B) nonlinear
C) hyperbolic
D) elliptic
E) parabolic

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
28
In the previous three problems, the solution of the original problem is
A)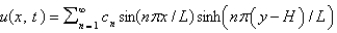 , where
, where 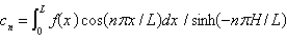
B)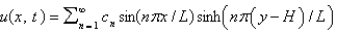 , where
, where 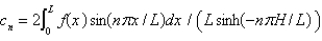
C)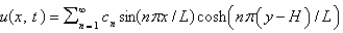 , where
, where 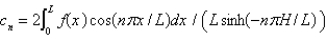
D)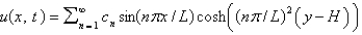 , where
, where 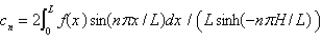
E)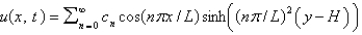 , where
, where 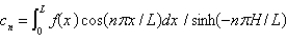
A)
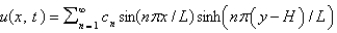 , where
, where 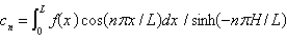
B)
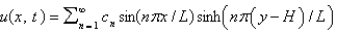 , where
, where 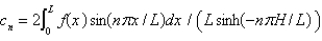
C)
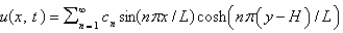 , where
, where 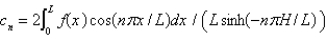
D)
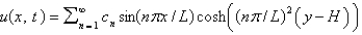 , where
, where 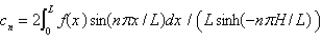
E)
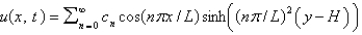 , where
, where 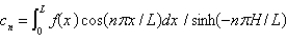

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
29
In the previous two problems, the product solutions are
A)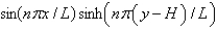
B)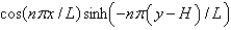
C)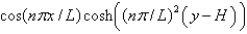
D)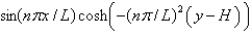
E)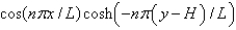
A)
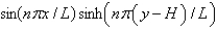
B)
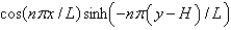
C)
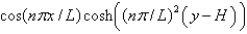
D)
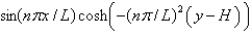
E)
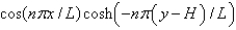

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
30
The differential equation 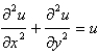 is
is
A) first order, linear, homogeneous
B) first order, linear, non-homogeneous
C) second order, nonlinear
D) second order, linear, homogeneous
E) second order, linear, non-homogeneous
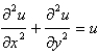 is
isA) first order, linear, homogeneous
B) first order, linear, non-homogeneous
C) second order, nonlinear
D) second order, linear, homogeneous
E) second order, linear, non-homogeneous

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
31
In the problem 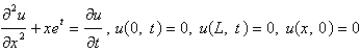 , the eigenvalues and eigenfunctions of the underlying homogeneous problem are
, the eigenvalues and eigenfunctions of the underlying homogeneous problem are
A)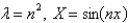
B)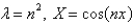
C)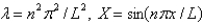
D)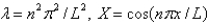
E)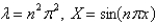
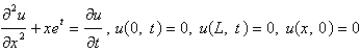 , the eigenvalues and eigenfunctions of the underlying homogeneous problem are
, the eigenvalues and eigenfunctions of the underlying homogeneous problem areA)
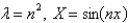
B)
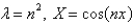
C)
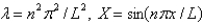
D)
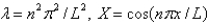
E)
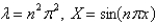

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
32
The quantity of heat in an element of a rod of mass 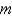 is proportional to Select all that apply.
is proportional to Select all that apply.
A) mass
B) thermal conductivity
C) specific heat
D) thermal diffusivity
E) temperature
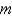 is proportional to Select all that apply.
is proportional to Select all that apply.A) mass
B) thermal conductivity
C) specific heat
D) thermal diffusivity
E) temperature

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
33
In the previous two problems, the solution for 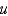 takes the form
takes the form
A)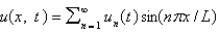
B)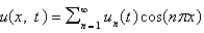
C)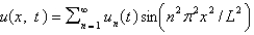
D)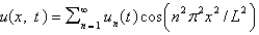
E)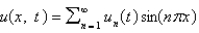
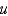 takes the form
takes the formA)
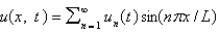
B)
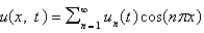
C)
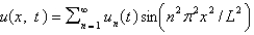
D)
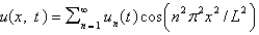
E)
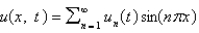

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
34
In the previous two problems, the product solutions are
A)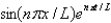
B)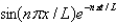
C)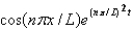
D)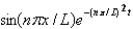
E)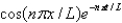
A)
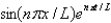
B)
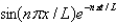
C)
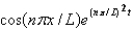
D)
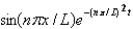
E)
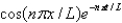

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
35
Consider the equation 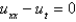 with conditions
with conditions 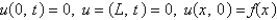 . When separating variables with
. When separating variables with 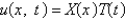 , the resulting problems for
, the resulting problems for 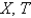 are
are
A)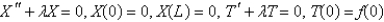
B)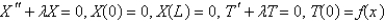
C)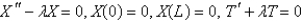
D)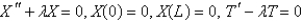
E)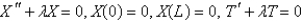
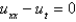 with conditions
with conditions 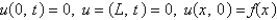 . When separating variables with
. When separating variables with 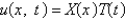 , the resulting problems for
, the resulting problems for 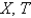 are
areA)
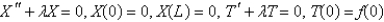
B)
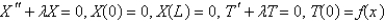
C)
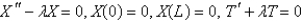
D)
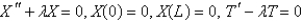
E)
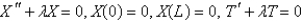

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
36
In the previous three problems, the solution of the original problem is
A)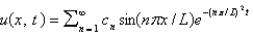 , where
, where 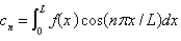
B)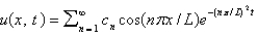 , where
, where 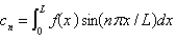
C)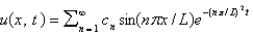 , where
, where 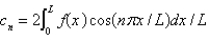
D)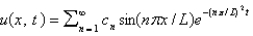 , where
, where 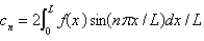
E)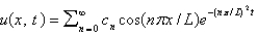 , where
, where 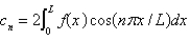
A)
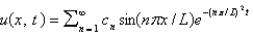 , where
, where 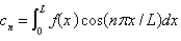
B)
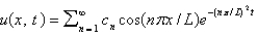 , where
, where 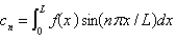
C)
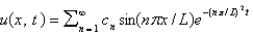 , where
, where 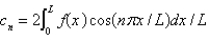
D)
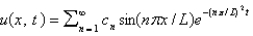 , where
, where 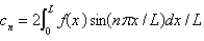
E)
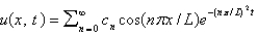 , where
, where 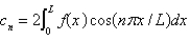

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
37
The general solution of 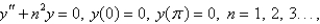 is
is
A)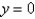
B)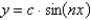
C)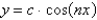
D)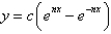
E)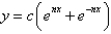
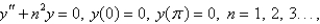 is
isA)
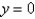
B)
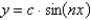
C)
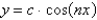
D)
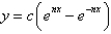
E)
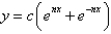

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
38
The solution of 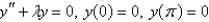 if
if 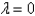 is
is
A)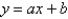
B)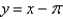
C)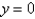
D)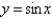
E)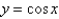
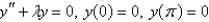 if
if 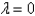 is
isA)
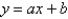
B)
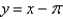
C)
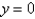
D)
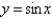
E)
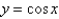

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
39
In the previous three problems, the solution for 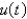 is
is
A)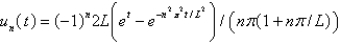
B)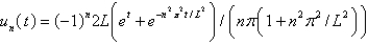
C)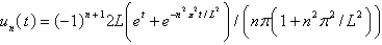
D)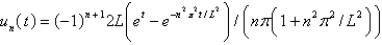
E)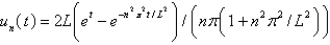
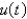 is
isA)
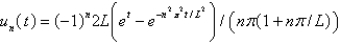
B)
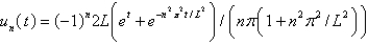
C)
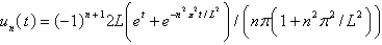
D)
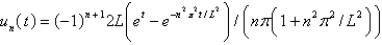
E)
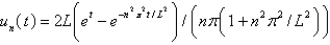

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
40
The differential equation 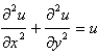 is Select all that apply.
is Select all that apply.
A) linear
B) nonlinear
C) hyperbolic
D) elliptic
E) parabolic
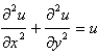 is Select all that apply.
is Select all that apply.A) linear
B) nonlinear
C) hyperbolic
D) elliptic
E) parabolic

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck


