Deck 13: Boundary-Value Problems in Other Coordinate Systems
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/40
Play
Full screen (f)
Deck 13: Boundary-Value Problems in Other Coordinate Systems
1
In the previous problem, the solution of the eigenvalue problem is
A)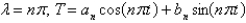
B)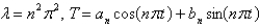
C)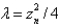 , where
, where 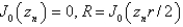
D)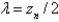 , where
, where 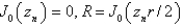
E)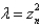 , where
, where 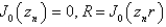
A)
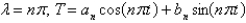
B)
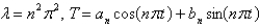
C)
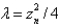 , where
, where 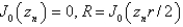
D)
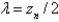 , where
, where 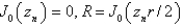
E)
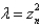 , where
, where 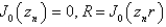
C
2
Using the separation of the previous problem, the equation for  becomes
becomes
A)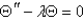
B)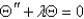
C)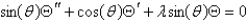
D)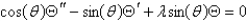
E)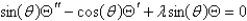
 becomes
becomesA)
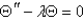
B)
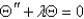
C)
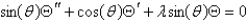
D)
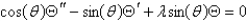
E)
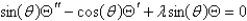
C
3
The two dimensional wave equation in polar coordinates is
A)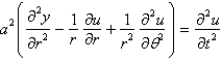
B)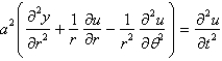
C)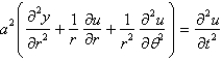
D)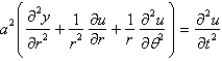
E)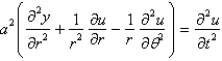
A)
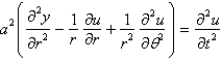
B)
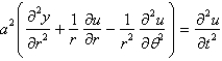
C)
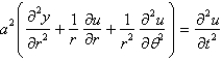
D)
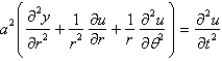
E)
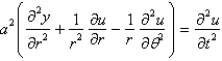
C
4
Consider the vibrations of a circular membrane of radius 2 clamped along the circumference, with an initial displacement of 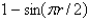 and an initial velocity of zero. The mathematical model for this situation is
and an initial velocity of zero. The mathematical model for this situation is
A)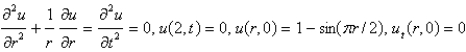
B)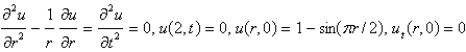
C)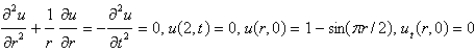
D)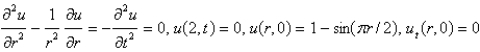
E)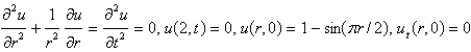
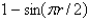 and an initial velocity of zero. The mathematical model for this situation is
and an initial velocity of zero. The mathematical model for this situation isA)
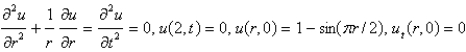
B)
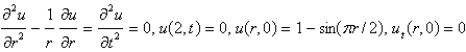
C)
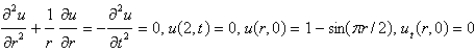
D)
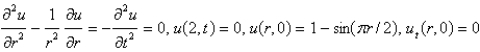
E)
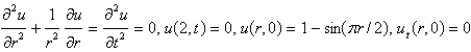

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
5
In the previous four problems, the infinite series solution of the original problem is (for certain values of the constants 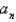 and
and 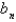 )
)
A)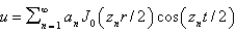
B)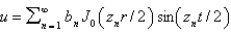
C)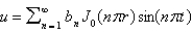
D)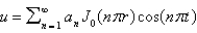
E)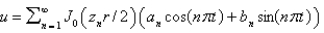
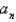 and
and 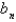 )
)A)
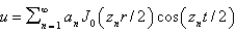
B)
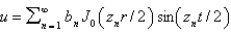
C)
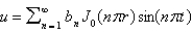
D)
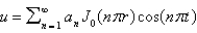
E)
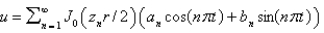

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
6
The equations relating Cartesian and spherical coordinates include Select all that apply.
A)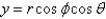
B)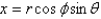
C)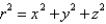
D)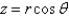
E)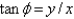
A)
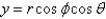
B)
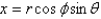
C)
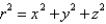
D)
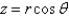
E)
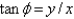

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
7
In the previous problem, separate variables using 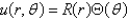 . The resulting problems are
. The resulting problems are
A)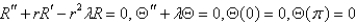
B)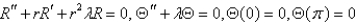
C)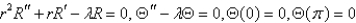
D)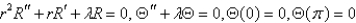
E)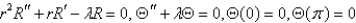
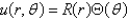 . The resulting problems are
. The resulting problems areA)
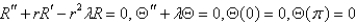
B)
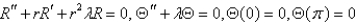
C)
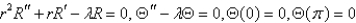
D)
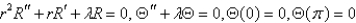
E)
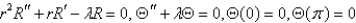

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
8
The solution of 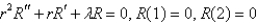 is
is
A)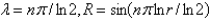
B)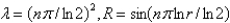
C)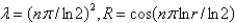
D)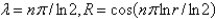
E) none of the above
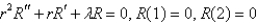 is
isA)
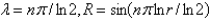
B)
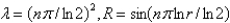
C)
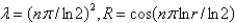
D)
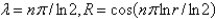
E) none of the above

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
9
In the previous four problems, the infinite series solution of the original problem is 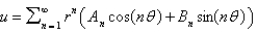 where Select all that apply.
where Select all that apply.
A)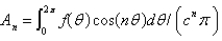
B)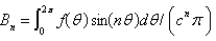
C)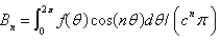
D)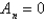
E)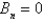
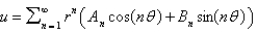 where Select all that apply.
where Select all that apply.A)
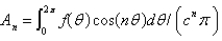
B)
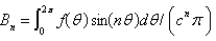
C)
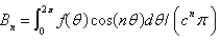
D)
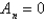
E)
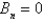

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
10
In changing from Cartesian to spherical coordinates, 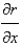 becomes
becomes
A)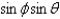
B)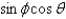
C)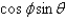
D)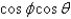
E)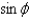
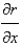 becomes
becomesA)
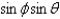
B)
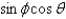
C)
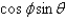
D)
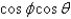
E)
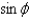

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
11
In the three previous problems, the product solutions are
A)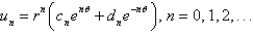
B)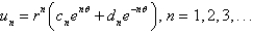
C)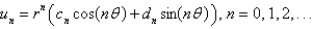
D)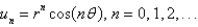
E)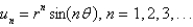
A)
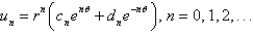
B)
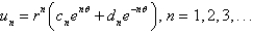
C)
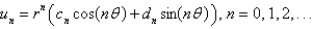
D)
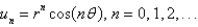
E)
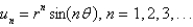

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
12
In the previous three problems, the solution for 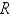 is
is
A)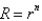
B)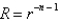
C)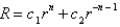
D)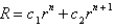
E)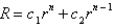
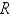 is
isA)
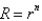
B)
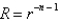
C)
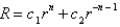
D)
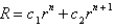
E)
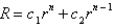

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
13
In the previous problem, the solution of the eigenvalue problem is
A)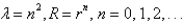
B)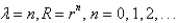
C)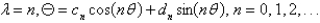
D)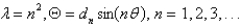
E)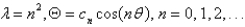
A)
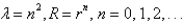
B)
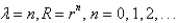
C)
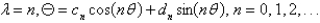
D)
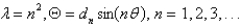
E)
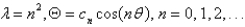

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
14
In separating variables, using, 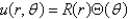 , in the equation
, in the equation 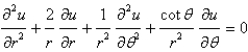 , the resulting equation for
, the resulting equation for 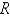 and is
and is
A)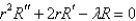
B)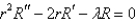
C)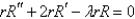
D)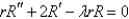
E)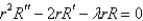
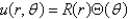 , in the equation
, in the equation 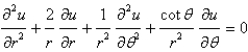 , the resulting equation for
, the resulting equation for 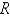 and is
and isA)
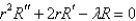
B)
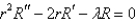
C)
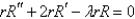
D)
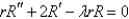
E)
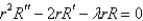

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
15
In the previous problem, if we also require that  be bounded everywhere, the solution of the eigenvalue problem is
be bounded everywhere, the solution of the eigenvalue problem is
A)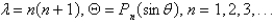
B)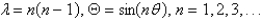
C)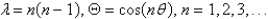
D)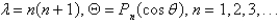
E)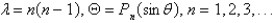
 be bounded everywhere, the solution of the eigenvalue problem is
be bounded everywhere, the solution of the eigenvalue problem isA)
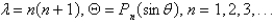
B)
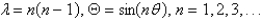
C)
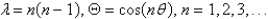
D)
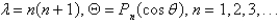
E)
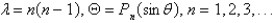

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
16
In changing from Cartesian to polar coordinates, 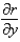 is
is
A)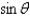
B)
C)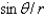
D)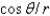
E)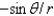
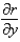 is
isA)
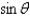
B)

C)
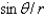
D)
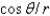
E)
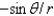

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
17
In changing from Cartesian to polar coordinates, 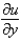 is
is
A)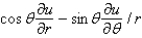
B)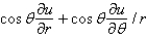
C)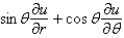
D)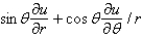
E)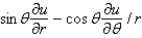
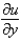 is
isA)
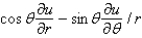
B)
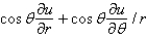
C)
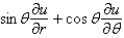
D)
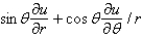
E)
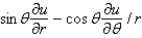

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
18
In the previous problem, after separating variables using 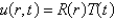 . the resulting problems are
. the resulting problems are
A)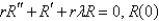 is bounded
is bounded 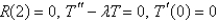
B)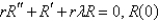 is bounded
is bounded 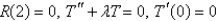
C)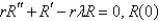 is bounded
is bounded 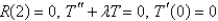
D)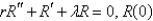 is bounded
is bounded 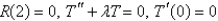
E)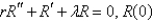 is bounded
is bounded 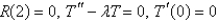
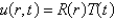 . the resulting problems are
. the resulting problems areA)
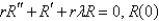 is bounded
is bounded 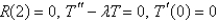
B)
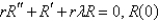 is bounded
is bounded 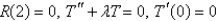
C)
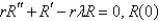 is bounded
is bounded 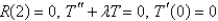
D)
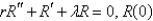 is bounded
is bounded 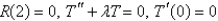
E)
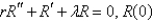 is bounded
is bounded 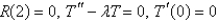

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
19
Consider the steady-state temperature distribution in a circular disc of radius 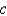 centere at the origin, with temperature given as a function,
centere at the origin, with temperature given as a function, 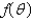 on the boundary
on the boundary 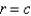 and zero on the boundaries
and zero on the boundaries 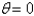 and
and 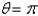 The mathematical model of this situation is
The mathematical model of this situation is
A)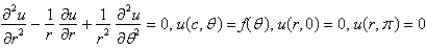
B)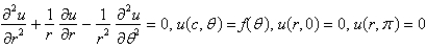
C)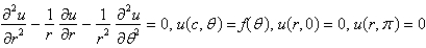
D)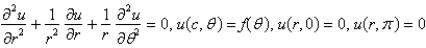
E)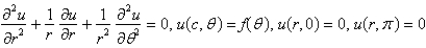
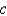 centere at the origin, with temperature given as a function,
centere at the origin, with temperature given as a function, 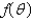 on the boundary
on the boundary 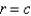 and zero on the boundaries
and zero on the boundaries 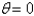 and
and 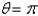 The mathematical model of this situation is
The mathematical model of this situation isA)
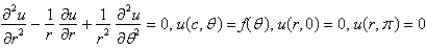
B)
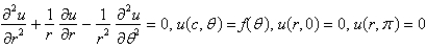
C)
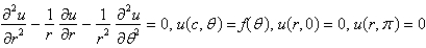
D)
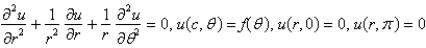
E)
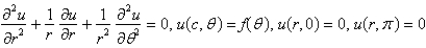

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
20
In the previous three problems, the product solutions are
A)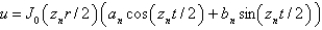
B)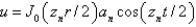
C)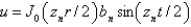
D)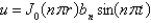
E)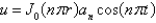
A)
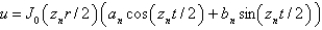
B)
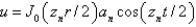
C)
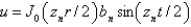
D)
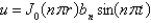
E)
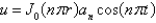

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
21
In the previous problem, the solution of the eigenvalue problem is
A)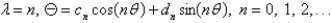
B)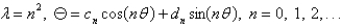
C)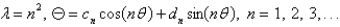
D)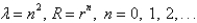
E)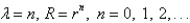
A)
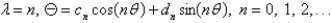
B)
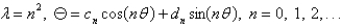
C)
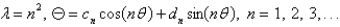
D)
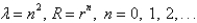
E)
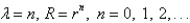

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
22
In changing from Cartesian to polar coordinates, 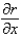 is
is
A)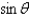
B)
C)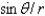
D)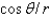
E)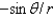
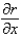 is
isA)
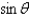
B)

C)
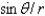
D)
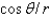
E)
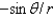

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
23
In the previous problem, separate variables using 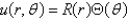 . The resulting problems are
. The resulting problems are
A)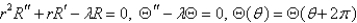
B)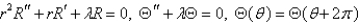
C)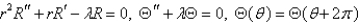
D)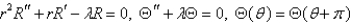
E)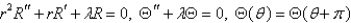
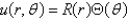 . The resulting problems are
. The resulting problems areA)
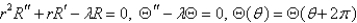
B)
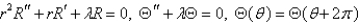
C)
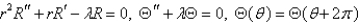
D)
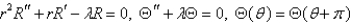
E)
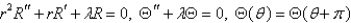

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
24
In changing from Cartesian to polar coordinates, 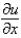 is
is
A)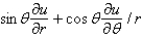
B)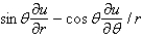
C)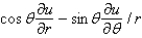
D)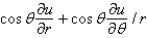
E)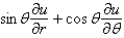
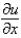 is
isA)
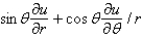
B)
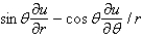
C)
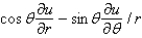
D)
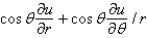
E)
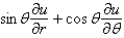

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
25
The relationships between Cartesian and spherical coordinates are Select all that apply.
A)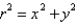
B)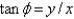
C)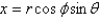
D)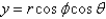
E)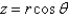
A)
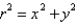
B)
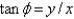
C)
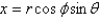
D)
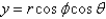
E)
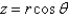

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
26
In the previous three problems, the product solutions are
A)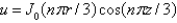
B)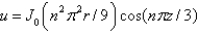
C)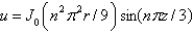
D)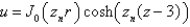
E)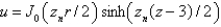
A)
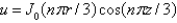
B)
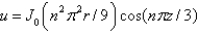
C)
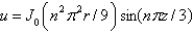
D)
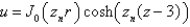
E)
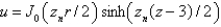

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
27
Consider the steady-state temperature distribution in a circular cylinder of radius 2 and height 3, with zero temperature at 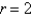 and at
and at 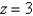 and a temperature of 10 at
and a temperature of 10 at 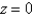 . The mathematical model for this problem is
. The mathematical model for this problem is
A)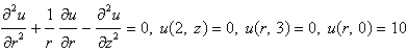
B)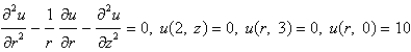
C)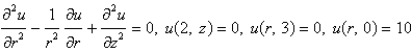
D)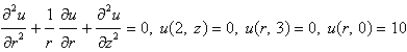
E)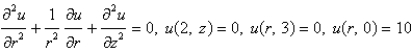
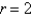 and at
and at 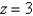 and a temperature of 10 at
and a temperature of 10 at 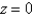 . The mathematical model for this problem is
. The mathematical model for this problem isA)
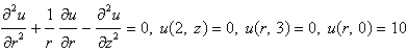
B)
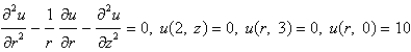
C)
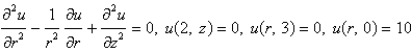
D)
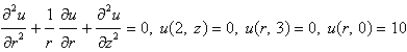
E)
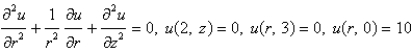

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
28
In the problem 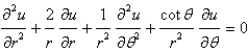 , separate variables, using
, separate variables, using 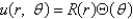 . The resulting problems for
. The resulting problems for 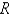 and
and  are
are
A)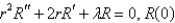 is bounded;
is bounded; 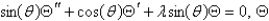 is bounded on
is bounded on 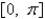 .
.
B)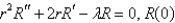 is bounded;
is bounded; 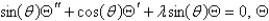 is bounded on
is bounded on 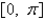 .
.
C)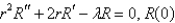 is bounded;
is bounded; 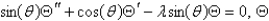 is bounded on
is bounded on 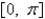 .
.
D)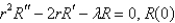 is bounded;
is bounded; 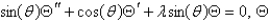 is bounded on
is bounded on 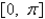 .
.
E)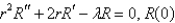 is bounded;
is bounded; 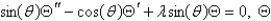 is bounded on
is bounded on 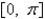 .
.
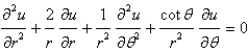 , separate variables, using
, separate variables, using 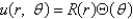 . The resulting problems for
. The resulting problems for 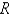 and
and  are
areA)
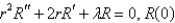 is bounded;
is bounded; 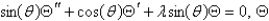 is bounded on
is bounded on 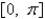 .
.B)
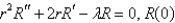 is bounded;
is bounded; 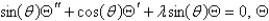 is bounded on
is bounded on 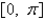 .
.C)
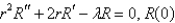 is bounded;
is bounded; 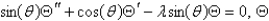 is bounded on
is bounded on 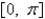 .
.D)
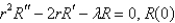 is bounded;
is bounded; 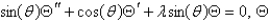 is bounded on
is bounded on 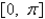 .
.E)
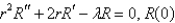 is bounded;
is bounded; 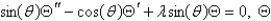 is bounded on
is bounded on 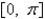 .
.
Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
29
The Laplacian in polar coordinates is
A)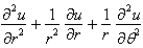
B)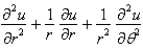
C)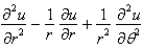
D)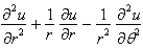
E)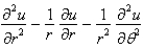
A)
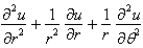
B)
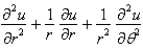
C)
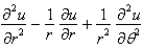
D)
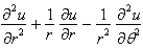
E)
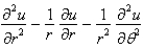

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
30
Consider the steady-state temperature distribution in a circular disc of radius 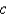 centere at the origin, with temperature given as a function,
centere at the origin, with temperature given as a function, 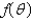 on the boundary. The mathematical model of this situation is
on the boundary. The mathematical model of this situation is
A)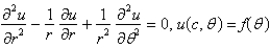
B)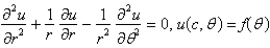
C)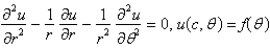
D)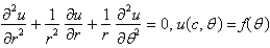
E)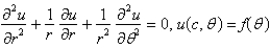
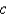 centere at the origin, with temperature given as a function,
centere at the origin, with temperature given as a function, 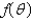 on the boundary. The mathematical model of this situation is
on the boundary. The mathematical model of this situation isA)
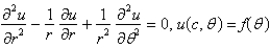
B)
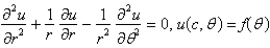
C)
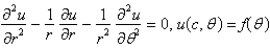
D)
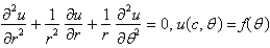
E)
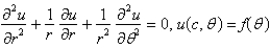

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
31
In the previous four problems, the infinite series solution is (for certain values of the constants)
A)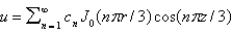
B)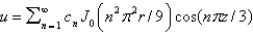
C)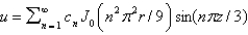
D)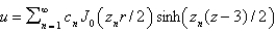
E)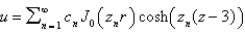
A)
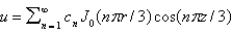
B)
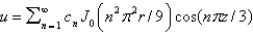
C)
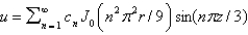
D)
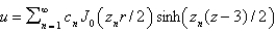
E)
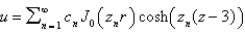

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
32
In the three previous problems, the product solutions are
A)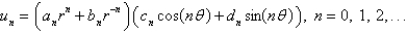
B)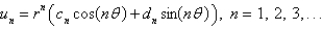
C)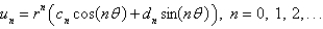
D)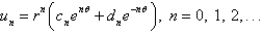
E)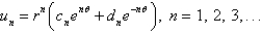
A)
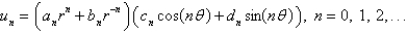
B)
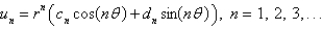
C)
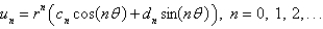
D)
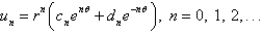
E)
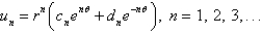

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
33
The solution of 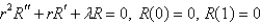 is
is
A)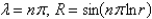
B)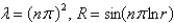
C)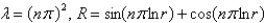
D)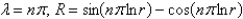
E) none of the above
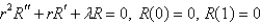 is
isA)
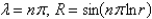
B)
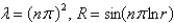
C)
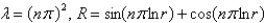
D)
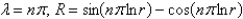
E) none of the above

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
34
In the previous problem, the solution of the eigenvalue problem is
A)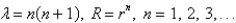
B)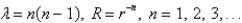
C)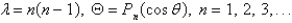
D)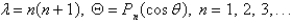
E)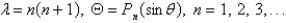
A)
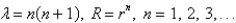
B)
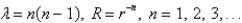
C)
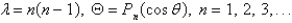
D)
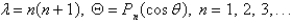
E)
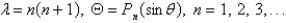

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
35
In the previous two problems, the product solutions are
A)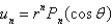
B)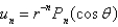
C)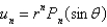
D)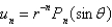
E) none of the above
A)
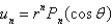
B)
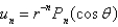
C)
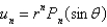
D)
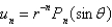
E) none of the above

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
36
In the previous problem, after separating variables, the resulting problems are
A)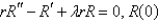 is bounded,
is bounded, 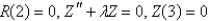
B)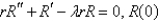 is bounded,
is bounded, 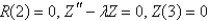
C)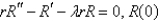 is bounded,
is bounded, 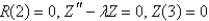
D)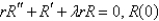 is bounded,
is bounded, 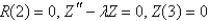
E)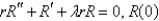 is bounded,
is bounded, 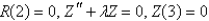
A)
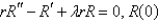 is bounded,
is bounded, 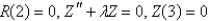
B)
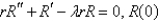 is bounded,
is bounded, 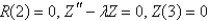
C)
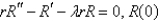 is bounded,
is bounded, 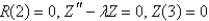
D)
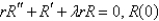 is bounded,
is bounded, 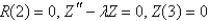
E)
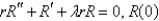 is bounded,
is bounded, 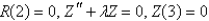

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
37
When changing from Cartesian to spherical coordinates, 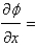
A)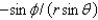
B)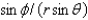
C)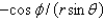
D)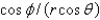
E)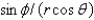
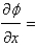
A)
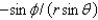
B)
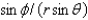
C)
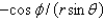
D)
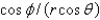
E)
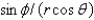

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
38
In the previous four problems, the infinite series solution of the original problem is 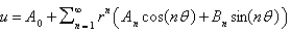 where Select all that apply.
where Select all that apply.
A)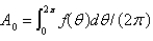
B)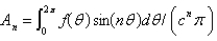
C)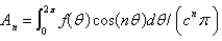
D)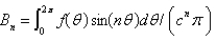
E)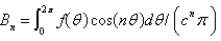
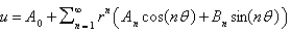 where Select all that apply.
where Select all that apply.A)
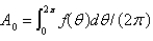
B)
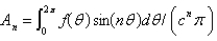
C)
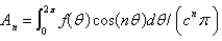
D)
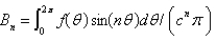
E)
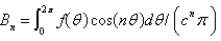

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
39
In the previous problem, the solution of the eigenvalue problem is
A)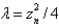 , where
, where 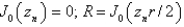
B)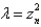 , where
, where 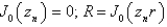
C)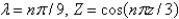
D)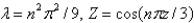
E)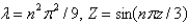
A)
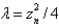 , where
, where 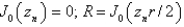
B)
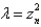 , where
, where 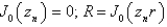
C)
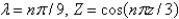
D)
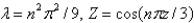
E)
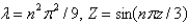

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
40
When changing from Cartesian to spherical coordinates, 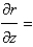
A)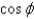
B)
C)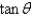
D)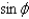
E)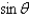
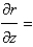
A)
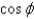
B)

C)
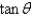
D)
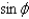
E)
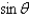

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck


