Deck 10: Plane Autonomous Systems
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/40
Play
Full screen (f)
Deck 10: Plane Autonomous Systems
1
The geometric configuration of the solutions of 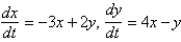 in the phase plane is
in the phase plane is
A) stable node
B) unstable node
C) stable spiral point
D) unstable spiral point
E) saddle point
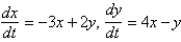 in the phase plane is
in the phase plane isA) stable node
B) unstable node
C) stable spiral point
D) unstable spiral point
E) saddle point
E
2
Assume a bead of mass  slides along the curve
slides along the curve  . Also assume that there is a damping force acting in the direction opposite to the velocity and proportional to the velocity, with proportionality constant
. Also assume that there is a damping force acting in the direction opposite to the velocity and proportional to the velocity, with proportionality constant 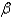 . The differential equation that describes the horizontal position of the bead is
. The differential equation that describes the horizontal position of the bead is
A)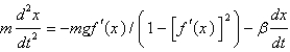
B)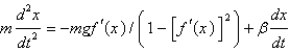
C)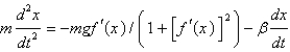
D)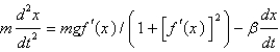
E)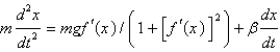
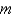 slides along the curve
slides along the curve 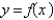 . Also assume that there is a damping force acting in the direction opposite to the velocity and proportional to the velocity, with proportionality constant
. Also assume that there is a damping force acting in the direction opposite to the velocity and proportional to the velocity, with proportionality constant 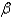 . The differential equation that describes the horizontal position of the bead is
. The differential equation that describes the horizontal position of the bead isA)
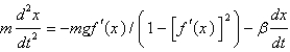
B)
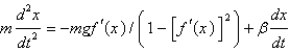
C)
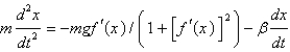
D)
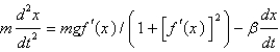
E)
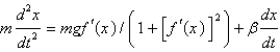
C
3
The values of 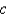 that make the system
that make the system 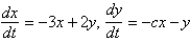 stable are
stable are
A)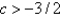
B)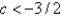
C) It is locally stable for all values of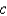 .
.
D) It is unstable for all values of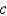 .
.
E)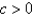
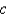 that make the system
that make the system 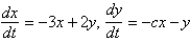 stable are
stable areA)
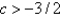
B)
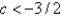
C) It is locally stable for all values of
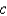 .
.D) It is unstable for all values of
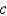 .
.E)
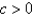
A
4
The constant solution of 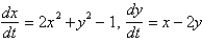 are
are
A)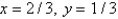
B)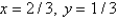 and
and 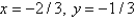
C)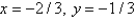
D)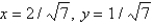
E)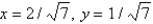 and
and 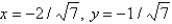
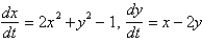 are
areA)
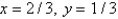
B)
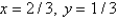 and
and 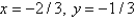
C)
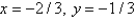
D)
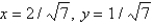
E)
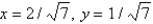 and
and 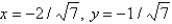

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
5
Which of the following systems are linear? Select all that apply.
A)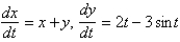
B)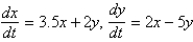
C)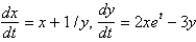
D)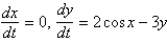
E)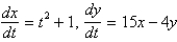
A)
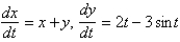
B)
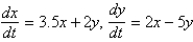
C)
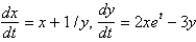
D)
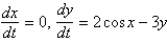
E)
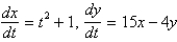

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
6
The critical point 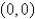 of the system
of the system 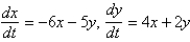 is Select all that apply.
is Select all that apply.
A) asymptotically stable
B) stable but not asymptotically stable
C) unstable
D) an attractor
E) a repeller
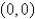 of the system
of the system 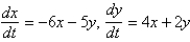 is Select all that apply.
is Select all that apply.A) asymptotically stable
B) stable but not asymptotically stable
C) unstable
D) an attractor
E) a repeller

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
7
The critical point 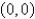 of the system
of the system 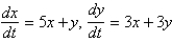 is Select all that apply.
is Select all that apply.
A) asymptotically stable
B) stable but not asymptotically stable
C) unstable
D) an attractor
E) a repeller
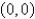 of the system
of the system 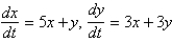 is Select all that apply.
is Select all that apply.A) asymptotically stable
B) stable but not asymptotically stable
C) unstable
D) an attractor
E) a repeller

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
8
The solution of the system 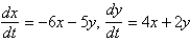 is
is
A)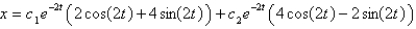 ,
, 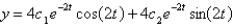
B)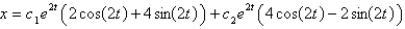 ,
, 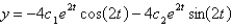
C)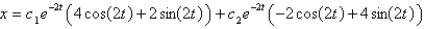 ,
, 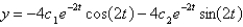
D)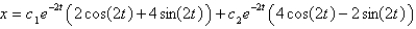 ,
, 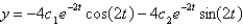
E)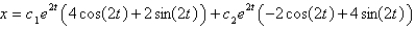 ,
, 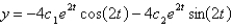
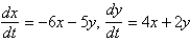 is
isA)
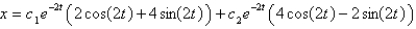 ,
, 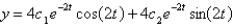
B)
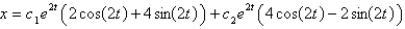 ,
, 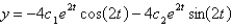
C)
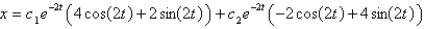 ,
, 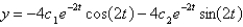
D)
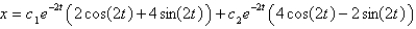 ,
, 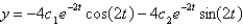
E)
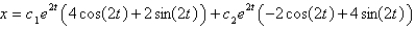 ,
, 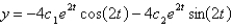

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
9
The Jacobian matrix of the system 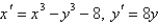 at the critical point
at the critical point 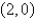
A)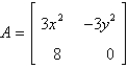
B)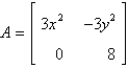
C)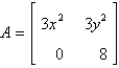
D)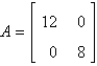
E)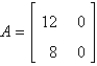
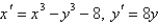 at the critical point
at the critical point 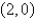
A)
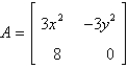
B)
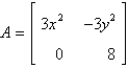
C)
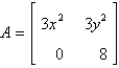
D)
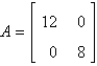
E)
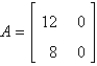

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
10
The solution of the system 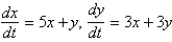 is
is
A)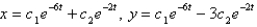
B)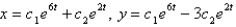
C)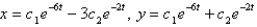
D)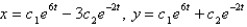
E)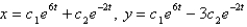
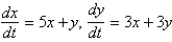 is
isA)
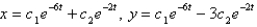
B)
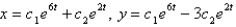
C)
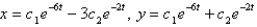
D)
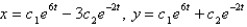
E)
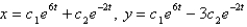

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
11
The initial value problem 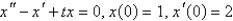 can be rewritten as the system
can be rewritten as the system
A)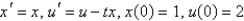
B)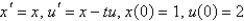
C)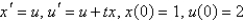
D)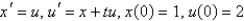
E)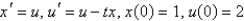
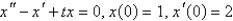 can be rewritten as the system
can be rewritten as the systemA)
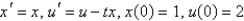
B)
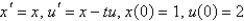
C)
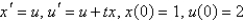
D)
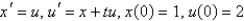
E)
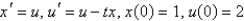

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
12
The geometric configuration of the solutions of 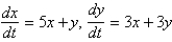 in the phase plane is
in the phase plane is
A) stable spiral point
B) unstable spiral point
C) stable node
D) unstable node
E) saddle point
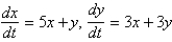 in the phase plane is
in the phase plane isA) stable spiral point
B) unstable spiral point
C) stable node
D) unstable node
E) saddle point

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
13
The critical points of the system 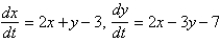 are
are
A)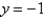
B)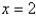
C)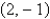
D)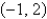
E)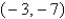
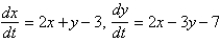 are
areA)
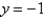
B)
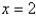
C)
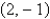
D)
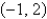
E)
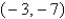

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
14
Consider the differential equation 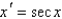 . The point
. The point 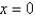 is
is
A) a stable critical point
B) an unstable critical point
C) not a critical point
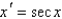 . The point
. The point 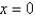 is
isA) a stable critical point
B) an unstable critical point
C) not a critical point

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
15
The critical point 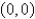 of the system
of the system 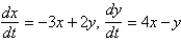 is Select all that apply.
is Select all that apply.
A) asymptotically stable
B) stable but not asymptotically stable
C) unstable
D) an attractor
E) a repeller
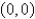 of the system
of the system 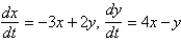 is Select all that apply.
is Select all that apply.A) asymptotically stable
B) stable but not asymptotically stable
C) unstable
D) an attractor
E) a repeller

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
16
Which of the following systems are autonomous? Select all that apply.
A)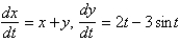
B)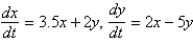
C)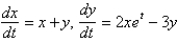
D)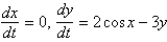
E)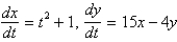
A)
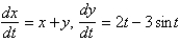
B)
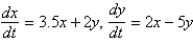
C)
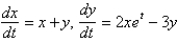
D)
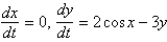
E)
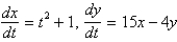

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
17
The critical points of the system 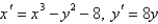 are
are
A)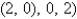
B)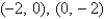
C)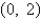
D)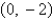
E) none of the above
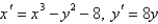 are
areA)
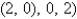
B)
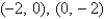
C)
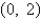
D)
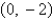
E) none of the above

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
18
The solution of the system 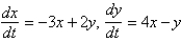 is
is
A)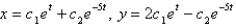
B)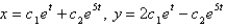
C)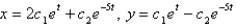
D)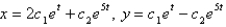
E)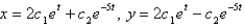
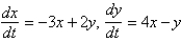 is
isA)
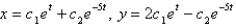
B)
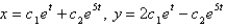
C)
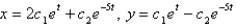
D)
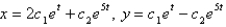
E)
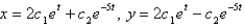

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
19
The geometric configuration of the solutions of 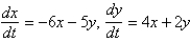 in the phase plane is
in the phase plane is
A) stable node
B) unstable node
C) stable spiral point
D) unstable spiral point
E) saddle point
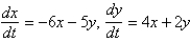 in the phase plane is
in the phase plane isA) stable node
B) unstable node
C) stable spiral point
D) unstable spiral point
E) saddle point

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
20
Consider the differential equation 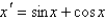 . The point
. The point 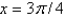 is
is
A) a stable critical point
B) an unstable critical point
C) not a critical point
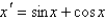 . The point
. The point 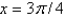 is
isA) a stable critical point
B) an unstable critical point
C) not a critical point

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
21
The geometric configuration of the solutions of 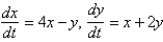 in the phase plane is
in the phase plane is
A) degenerate stable node
B) degenerate unstable node
C) stable spiral point
D) unstable spiral point
E) saddle point
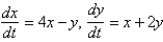 in the phase plane is
in the phase plane isA) degenerate stable node
B) degenerate unstable node
C) stable spiral point
D) unstable spiral point
E) saddle point

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
22
The differential equation 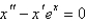 can be rewritten as the system
can be rewritten as the system
A)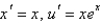
B)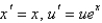
C)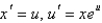
D)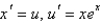
E)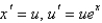
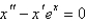 can be rewritten as the system
can be rewritten as the systemA)
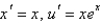
B)
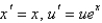
C)
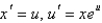
D)
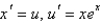
E)
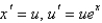

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
23
The Jacobian matrix of the system 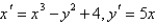 at the critical point
at the critical point 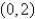
A)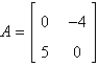
B)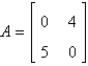
C)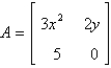
D)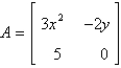
E)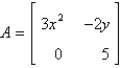
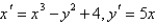 at the critical point
at the critical point 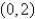
A)
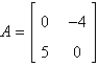
B)
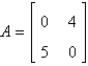
C)
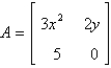
D)
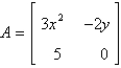
E)
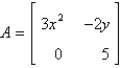

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
24
The critical point 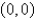 of the system
of the system 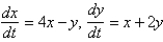 is Select all that apply.
is Select all that apply.
A) asymptotically stable
B) stable but not asymptotically stable
C) unstable
D) an attractor
E) a repeller
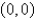 of the system
of the system 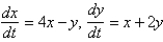 is Select all that apply.
is Select all that apply.A) asymptotically stable
B) stable but not asymptotically stable
C) unstable
D) an attractor
E) a repeller

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
25
Consider the differential equation 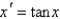 . The point
. The point 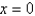 is
is
A) a stable critical point
B) an unstable critical point
C) not a critical point
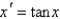 . The point
. The point 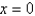 is
isA) a stable critical point
B) an unstable critical point
C) not a critical point

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
26
The critical point 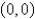 of the system
of the system 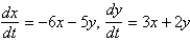 is Select all that apply.
is Select all that apply.
A) asymptotically stable
B) stable but not asymptotically stable
C) unstable
D) an attractor
E) a repeller
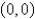 of the system
of the system 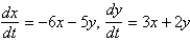 is Select all that apply.
is Select all that apply.A) asymptotically stable
B) stable but not asymptotically stable
C) unstable
D) an attractor
E) a repeller

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
27
Consider the differential equation 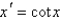 . The point
. The point 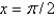 is
is
A) a stable critical point
B) an unstable critical point
C) not a critical point
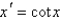 . The point
. The point 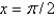 is
isA) a stable critical point
B) an unstable critical point
C) not a critical point

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
28
The solution of the system 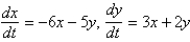 is
is
A)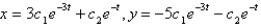
B)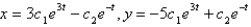
C)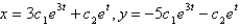
D)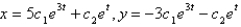
E)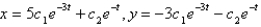
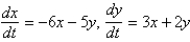 is
isA)
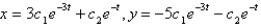
B)
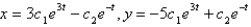
C)
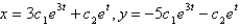
D)
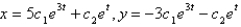
E)
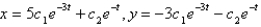

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
29
The values of 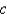 that make the system
that make the system 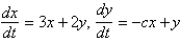 stable are
stable are
A)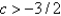
B)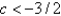
C) It is stable for all values of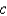 .
.
D) It is unstable for all values of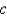 .
.
E)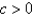
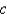 that make the system
that make the system 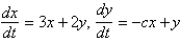 stable are
stable areA)
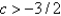
B)
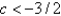
C) It is stable for all values of
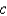 .
.D) It is unstable for all values of
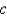 .
.E)
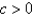

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
30
The geometric configuration of the solutions of 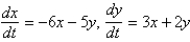 in the phase plane is
in the phase plane is
A) stable node
B) unstable node
C) stable spiral point
D) unstable spiral point
E) saddle point
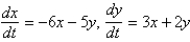 in the phase plane is
in the phase plane isA) stable node
B) unstable node
C) stable spiral point
D) unstable spiral point
E) saddle point

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
31
The critical points of the system 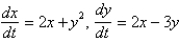 are
are
A)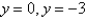
B)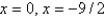
C)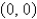
D)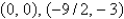
E)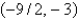
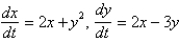 are
areA)
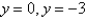
B)
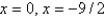
C)
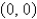
D)
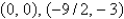
E)
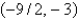

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
32
Which of the following systems are autonomous? Select all that apply.
A)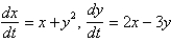
B)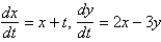
C)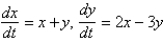
D)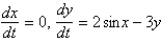
E)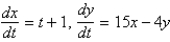
A)
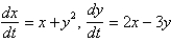
B)
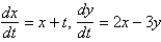
C)
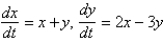
D)
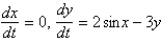
E)
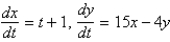

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
33
Which of the following systems are linear? Select all that apply.
A)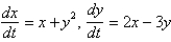
B)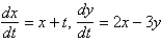
C)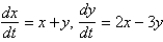
D)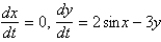
E)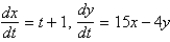
A)
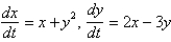
B)
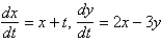
C)
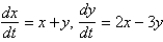
D)
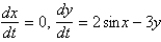
E)
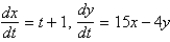

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
34
The Jacobian matrix of the system 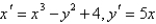 at the critical point
at the critical point 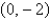
A)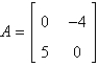
B)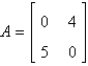
C)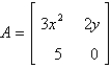
D)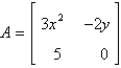
E)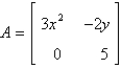
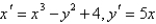 at the critical point
at the critical point 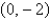
A)
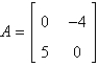
B)
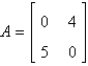
C)
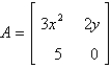
D)
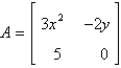
E)
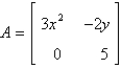

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
35
The critical point 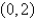 of the system
of the system 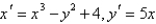 is a
is a
A) stable node
B) unstable node
C) stable spiral point
D) unstable spiral point
E) center point
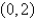 of the system
of the system 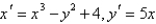 is a
is aA) stable node
B) unstable node
C) stable spiral point
D) unstable spiral point
E) center point

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
36
The solution of the system 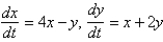 is
is
A)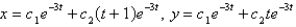
B)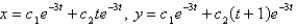
C)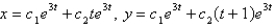
D)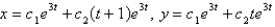
E)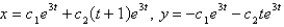
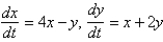 is
isA)
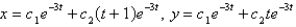
B)
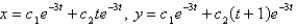
C)
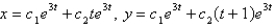
D)
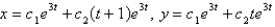
E)
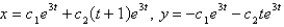

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
37
The critical point 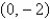 of the system
of the system 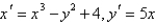 is a
is a
A) stable node
B) unstable node
C) stable spiral point
D) unstable spiral point
E) saddle point
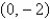 of the system
of the system 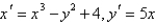 is a
is aA) stable node
B) unstable node
C) stable spiral point
D) unstable spiral point
E) saddle point

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
38
The only constant solution of 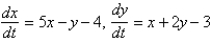 is
is
A)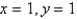
B)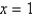
C)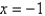
D)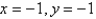
E)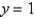
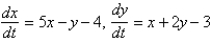 is
isA)
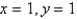
B)
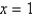
C)
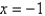
D)
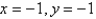
E)
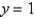

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
39
Assume that 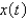 and
and 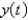 represent the populations of two competing species at time
represent the populations of two competing species at time 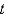 . The Lotka-Volterra competition model is
. The Lotka-Volterra competition model is
A)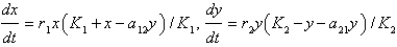
B)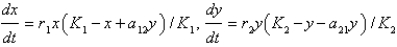
C)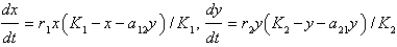
D)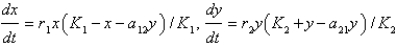
E)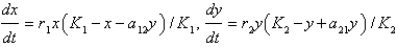
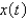 and
and 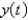 represent the populations of two competing species at time
represent the populations of two competing species at time 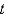 . The Lotka-Volterra competition model is
. The Lotka-Volterra competition model isA)
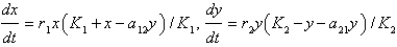
B)
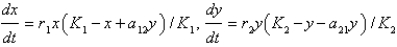
C)
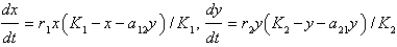
D)
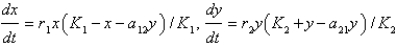
E)
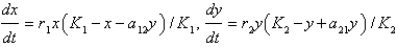

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
40
The critical points of the system 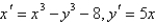 are
are
A)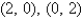
B)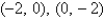
C)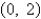
D)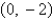
E) none of the above
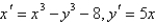 are
areA)
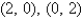
B)
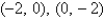
C)
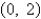
D)
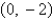
E) none of the above

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck


