Deck 6: Series Solutions of Linear Equations
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/40
Play
Full screen (f)
Deck 6: Series Solutions of Linear Equations
1
The recurrence relation for the power series solution about 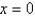 of the differential equation
of the differential equation 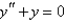 is
is
A)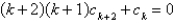
B)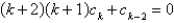
C)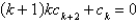
D)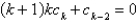
E)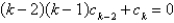
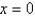 of the differential equation
of the differential equation 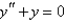 is
isA)
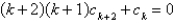
B)
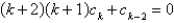
C)
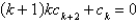
D)
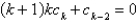
E)
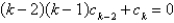
A
2
A power series solution about 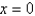 of the differential equation
of the differential equation 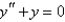 is
is
A)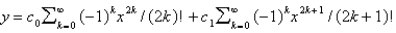
B)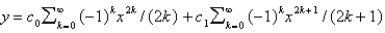
C)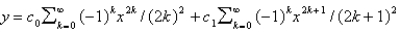
D)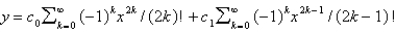
E)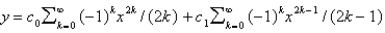
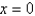 of the differential equation
of the differential equation 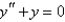 is
isA)
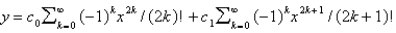
B)
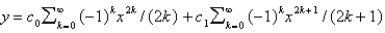
C)
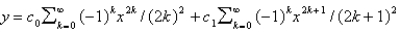
D)
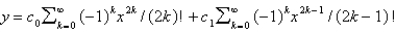
E)
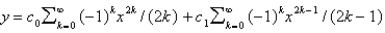
A
3
For the equation 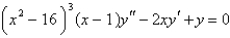 , the point
, the point 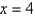 is
is
A) an ordinary point
B) a regular singular point
C) an irregular singular point
D) a special point
E) none of the above
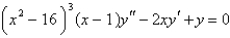 , the point
, the point 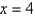 is
isA) an ordinary point
B) a regular singular point
C) an irregular singular point
D) a special point
E) none of the above
C
4
The solution of the previous problem is
A)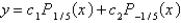
B)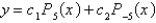
C)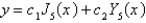
D)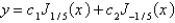
E)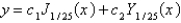
A)
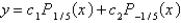
B)
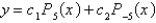
C)
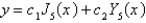
D)
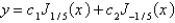
E)
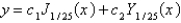

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
5
The interval of convergence of the power series in the previous problem is
A)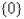
B)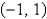
C)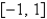
D)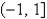
E)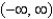
A)
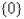
B)
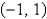
C)
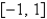
D)
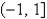
E)
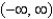

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
6
Consider the differential equation 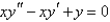 . The indicial equation is
. The indicial equation is 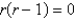 . The recurrence relation is
. The recurrence relation is 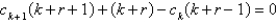 . A series solution corresponding to the indicial root
. A series solution corresponding to the indicial root 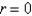 is
is
A)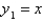
B)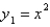
C)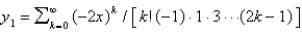
D)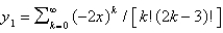
E)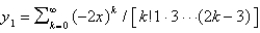
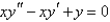 . The indicial equation is
. The indicial equation is 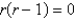 . The recurrence relation is
. The recurrence relation is 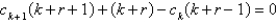 . A series solution corresponding to the indicial root
. A series solution corresponding to the indicial root 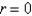 is
isA)
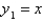
B)
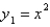
C)
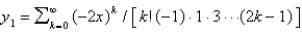
D)
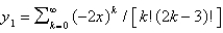
E)
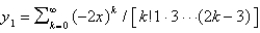

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
7
In the previous problem, a second solution is
A)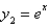
B)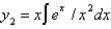
C)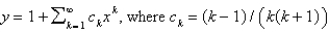
D)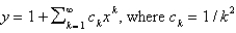
E) none of the above
A)
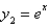
B)
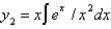
C)
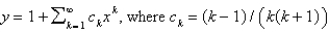
D)
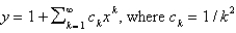
E) none of the above

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
8
For the equation 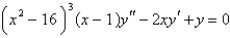 , the point
, the point 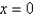 is
is
A) an ordinary point
B) a regular singular point
C) an irregular singular point
D) a special point
E) none of the above
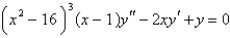 , the point
, the point 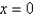 is
isA) an ordinary point
B) a regular singular point
C) an irregular singular point
D) a special point
E) none of the above

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
9
The differential equation is 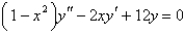 is
is
A) Bessel's equation of order 12
B) Bessel's equation of order 3
C) Legendre's equation of order 12
D) Legendre's equation of order 3
E) Legendre's equation of order 4
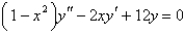 is
isA) Bessel's equation of order 12
B) Bessel's equation of order 3
C) Legendre's equation of order 12
D) Legendre's equation of order 3
E) Legendre's equation of order 4

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
10
For the equation 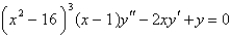 , the point
, the point 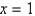 is
is
A) an ordinary point
B) a regular singular point
C) an irregular singular point
D) a special point
E) none of the above
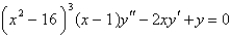 , the point
, the point 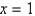 is
isA) an ordinary point
B) a regular singular point
C) an irregular singular point
D) a special point
E) none of the above

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
11
Find three positive values of 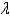 for which the differential equation
for which the differential equation 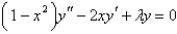 has polynomial solutions.
has polynomial solutions.
A) 2, 6, 12
B) 1, 2, 3
C) 1, 4, 9
D) 2, 4, 6
E) 2, 6, 10
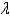 for which the differential equation
for which the differential equation 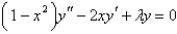 has polynomial solutions.
has polynomial solutions.A) 2, 6, 12
B) 1, 2, 3
C) 1, 4, 9
D) 2, 4, 6
E) 2, 6, 10

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
12
The solution of the recurrence relation in the previous problem is
A)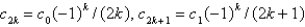
B)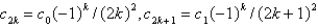
C)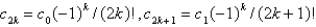
D)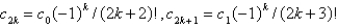
E)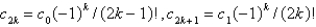
A)
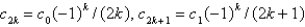
B)
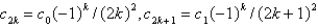
C)
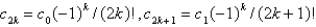
D)
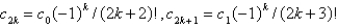
E)
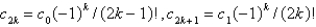

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
13
The solution of the previous problem is
A)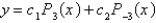
B)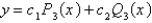 , where
, where 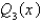 is given by an infinite series
is given by an infinite series
C)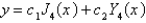
D)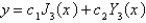
E)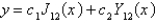
A)
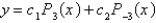
B)
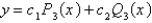 , where
, where 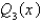 is given by an infinite series
is given by an infinite seriesC)
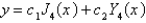
D)
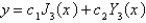
E)
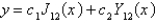

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
14
The singular points of the differential equation 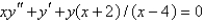 are
are
A) none
B) 0
C) 0,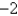
D) 0, 4
E) 0,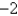 , 4
, 4
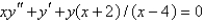 are
areA) none
B) 0
C) 0,
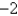
D) 0, 4
E) 0,
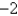 , 4
, 4
Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
15
The recurrence relation for the differential equation 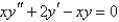 is
is
A)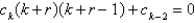
B)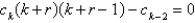
C)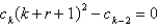
D)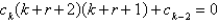
E)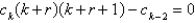
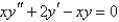 is
isA)
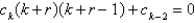
B)
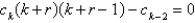
C)
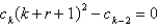
D)
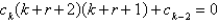
E)
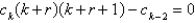

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
16
The radius of convergence of the power series 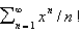 is
is
A) 0
B) 1
C) 2
D)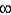
E) none of the above
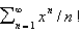 is
isA) 0
B) 1
C) 2
D)
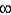
E) none of the above

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
17
The first four nonzero terms in the power series expansion of the function 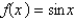 about
about 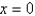 are
are
A)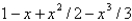
B)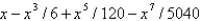
C)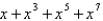
D)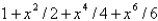
E)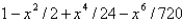
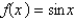 about
about 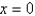 are
areA)
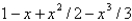
B)
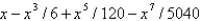
C)
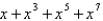
D)
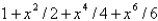
E)
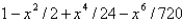

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
18
The differential equation 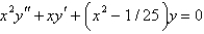 is
is
A) Bessel's equation of order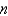
B) Bessel's equation of order 1/25
C) Bessel's equation of order 1/5
D) Legendre's equation of order 1/25
E) Legendre's equation of order 1/5
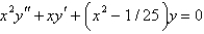 is
isA) Bessel's equation of order
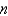
B) Bessel's equation of order 1/25
C) Bessel's equation of order 1/5
D) Legendre's equation of order 1/25
E) Legendre's equation of order 1/5

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
19
The radius of convergence of the power series solution of 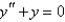 about
about 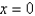 is
is
A) 0
B) 1
C) 2
D)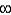
E) none of the above
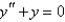 about
about 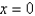 is
isA) 0
B) 1
C) 2
D)
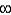
E) none of the above

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
20
The indicial equation for the differential equation 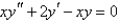 is
is
A)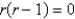
B)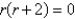
C)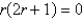
D)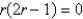
E)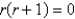
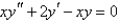 is
isA)
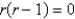
B)
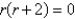
C)
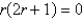
D)
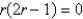
E)
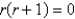

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
21
The differential equation 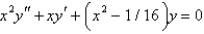 is
is
A) Bessel's equation of order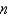
B) Bessel's equation of order 1/16
C) Bessel's equation of order 1/4
D) Legendre's equation of order 1/16
E) Legendre's equation of order 1/4
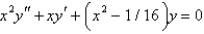 is
isA) Bessel's equation of order
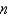
B) Bessel's equation of order 1/16
C) Bessel's equation of order 1/4
D) Legendre's equation of order 1/16
E) Legendre's equation of order 1/4

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
22
The solution of the previous problem is
A)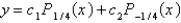
B)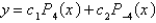
C)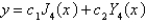
D)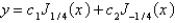
E)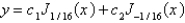
A)
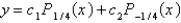
B)
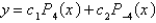
C)
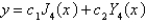
D)
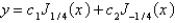
E)
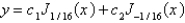

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
23
The radius of convergence of the power series 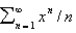 is
is
A) 0
B) 1
C) 2
D)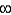
E) none of the above
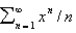 is
isA) 0
B) 1
C) 2
D)
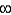
E) none of the above

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
24
The singular points of 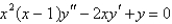 are
are 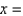 Select all that apply.
Select all that apply.
A) 2
B)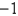
C) 0
D) 1
E) none of the above
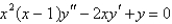 are
are 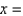 Select all that apply.
Select all that apply.A) 2
B)
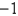
C) 0
D) 1
E) none of the above

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
25
The recurrence relation for the differential equation 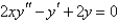 is
is
A)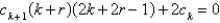
B)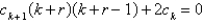
C)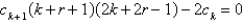
D)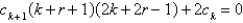
E)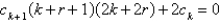
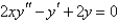 is
isA)
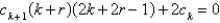
B)
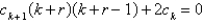
C)
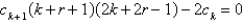
D)
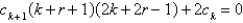
E)
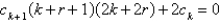

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
26
Consider the differential equation 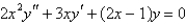 The indicial equation is
The indicial equation is 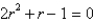 . The recurrence relation is
. The recurrence relation is 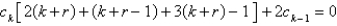 . A series solution corresponding to the indicial root
. A series solution corresponding to the indicial root 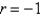 is
is 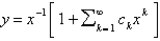 , where
, where
A)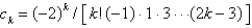
B)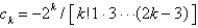
C)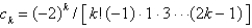
D)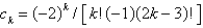
E)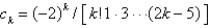
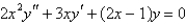 The indicial equation is
The indicial equation is 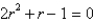 . The recurrence relation is
. The recurrence relation is 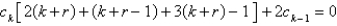 . A series solution corresponding to the indicial root
. A series solution corresponding to the indicial root 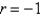 is
is 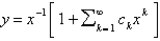 , where
, whereA)
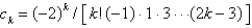
B)
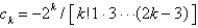
C)
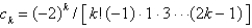
D)
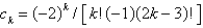
E)
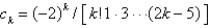

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
27
The interval of convergence of the power series in the previous problem is
A)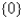
B)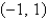
C)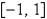
D)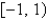
E)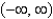
A)
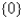
B)
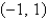
C)
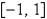
D)
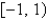
E)

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
28
The singular points of the differential equation 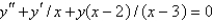 are
are
A) none
B) 0
C) 0, 2
D) 0, 3
E) 0, 2, 3
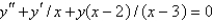 are
areA) none
B) 0
C) 0, 2
D) 0, 3
E) 0, 2, 3

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
29
For the differential equation 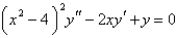 , the point
, the point 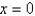 is
is
A) an ordinary point
B) a regular singular point
C) an irregular singular point
D) a special point
E) none of the above
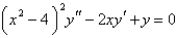 , the point
, the point 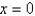 is
isA) an ordinary point
B) a regular singular point
C) an irregular singular point
D) a special point
E) none of the above

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
30
The recurrence relation for the power series solution about 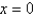 of the differential equation
of the differential equation 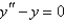 is (for
is (for 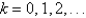 )
)
A)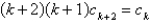
B)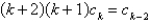
C)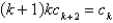
D)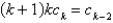
E)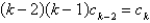
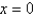 of the differential equation
of the differential equation 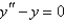 is (for
is (for 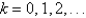 )
)A)
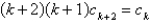
B)
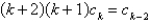
C)
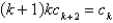
D)
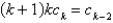
E)
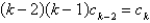

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
31
In the previous problem, a series solution corresponding to the indicial root 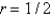 is
is 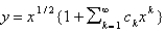 , where
, where
A)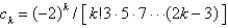
B)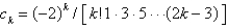
C)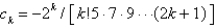
D)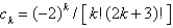
E)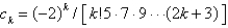
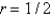 is
is 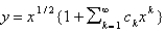 , where
, whereA)
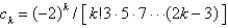
B)
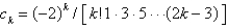
C)
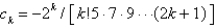
D)
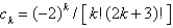
E)
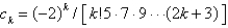

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
32
The radius of convergence of the power series solution of 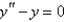 about
about 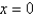 is
is
A) 0
B) 1
C) 2
D)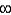
E) none of the above
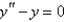 about
about 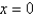 is
isA) 0
B) 1
C) 2
D)
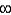
E) none of the above

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
33
The indicial equation for the differential equation 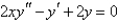 is
is
A)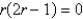
B)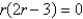
C)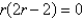
D)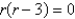
E)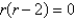
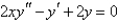 is
isA)
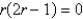
B)
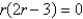
C)
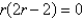
D)
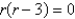
E)
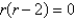

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
34
A power series solution about 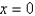 of the differential equation
of the differential equation 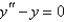 is
is
A)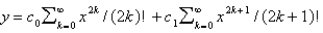
B)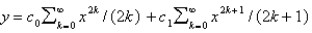
C)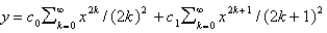
D)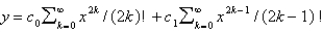
E)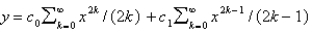
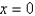 of the differential equation
of the differential equation 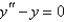 is
isA)
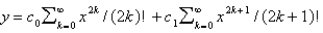
B)
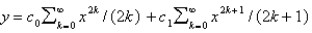
C)
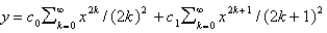
D)
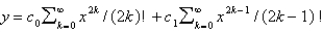
E)
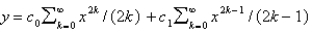

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
35
The solution of the previous problem is
A)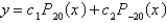
B)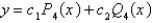 , where
, where 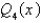 is given by an infinite series
is given by an infinite series
C)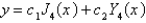
D)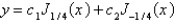
E)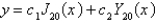
A)
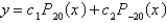
B)
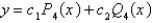 , where
, where 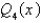 is given by an infinite series
is given by an infinite seriesC)
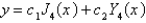
D)
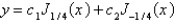
E)
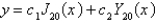

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
36
For the differential equation 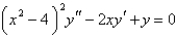 , the point
, the point 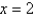 is
is
A) an ordinary point
B) a regular singular point
C) an irregular singular point
D) a special point
E) none of the above
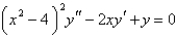 , the point
, the point 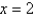 is
isA) an ordinary point
B) a regular singular point
C) an irregular singular point
D) a special point
E) none of the above

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
37
For the differential equation 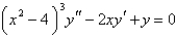 , the point
, the point 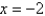 is
is
A) an ordinary point
B) a regular singular point
C) an irregular singular point
D) a special point
E) none of the above
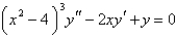 , the point
, the point 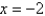 is
isA) an ordinary point
B) a regular singular point
C) an irregular singular point
D) a special point
E) none of the above

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
38
The first four terms in the power series expansion of the function 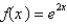 about
about 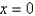 are
are
A)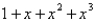
B)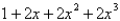
C)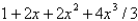
D)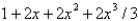
E)
 about
about  are
areA)
B)
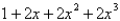
C)
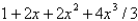
D)
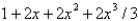
E)
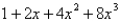

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
39
The solution of the recurrence relation in the previous problem is
A)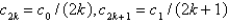
B)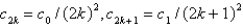
C)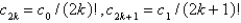
D)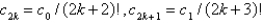
E)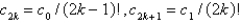
A)
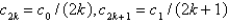
B)
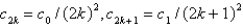
C)
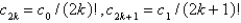
D)
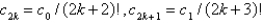
E)
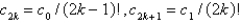

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
40
The differential equation is 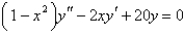 is
is
A) Bessel's equation of order 20
B) Bessel's equation of order 4
C) Legendre's equation of order n
D) Legendre's equation of order 20
E) Legendre's equation of order 4
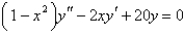 is
isA) Bessel's equation of order 20
B) Bessel's equation of order 4
C) Legendre's equation of order n
D) Legendre's equation of order 20
E) Legendre's equation of order 4

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck


