Deck 5: Modeling With Higher-Order Differential Equations
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/40
Play
Full screen (f)
Deck 5: Modeling With Higher-Order Differential Equations
1
The eigenvalue problem 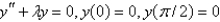 has the solution
has the solution
A)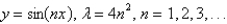
B)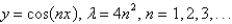
C)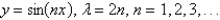
D)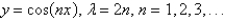
E) none of the above
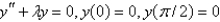 has the solution
has the solutionA)
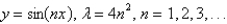
B)
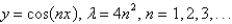
C)
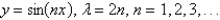
D)
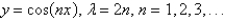
E) none of the above
E
2
A rocket is launched vertically upward with a speed 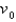 . Take the upward direction as positive and let the mass be m. Assume that the only force acting on the rocket is gravity, which is inversely proportional to the square of the distance from the center of the earth. Let
. Take the upward direction as positive and let the mass be m. Assume that the only force acting on the rocket is gravity, which is inversely proportional to the square of the distance from the center of the earth. Let 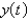 be the distance from the center of the earth at time,
be the distance from the center of the earth at time, 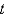 . the correct differential equation for the position of the rocket is
. the correct differential equation for the position of the rocket is
A)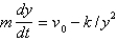
B)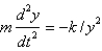
C)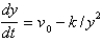
D)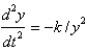
E) none of the above
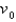 . Take the upward direction as positive and let the mass be m. Assume that the only force acting on the rocket is gravity, which is inversely proportional to the square of the distance from the center of the earth. Let
. Take the upward direction as positive and let the mass be m. Assume that the only force acting on the rocket is gravity, which is inversely proportional to the square of the distance from the center of the earth. Let 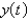 be the distance from the center of the earth at time,
be the distance from the center of the earth at time, 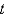 . the correct differential equation for the position of the rocket is
. the correct differential equation for the position of the rocket isA)
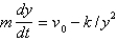
B)
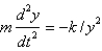
C)
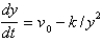
D)
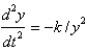
E) none of the above
B
3
A beam of length 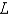 is simply supported at the left end embedded at right end. The weight density is constant,
is simply supported at the left end embedded at right end. The weight density is constant, 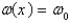 . Let
. Let 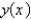 represent the deflection at point
represent the deflection at point 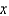 . The correct form of the boundary value problem for this beam is
. The correct form of the boundary value problem for this beam is
A)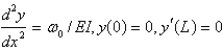
B)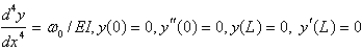
C)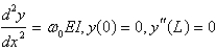
D)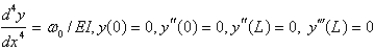
E) none of the above
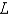 is simply supported at the left end embedded at right end. The weight density is constant,
is simply supported at the left end embedded at right end. The weight density is constant, 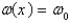 . Let
. Let 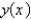 represent the deflection at point
represent the deflection at point 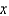 . The correct form of the boundary value problem for this beam is
. The correct form of the boundary value problem for this beam isA)
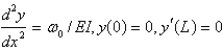
B)
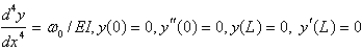
C)
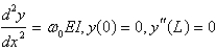
D)
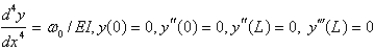
E) none of the above
B
4
The eigenvalue problem 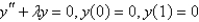 has the solution
has the solution
A)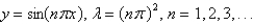
B)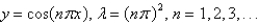
C)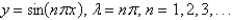
D)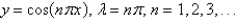
E) none of the above
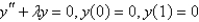 has the solution
has the solutionA)
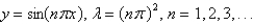
B)
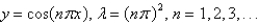
C)
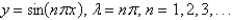
D)
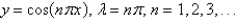
E) none of the above

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
5
A spring attached to the ceiling is stretched 2.45 meters by a four kilogram mass. The value of the Hooke's Law spring constant, 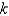 , is
, is
A) 1/4 meter-Newton
B) 4 meter-Newtons
C) 1/4 Newton per meter
D) 16 Newtons per meter
E) none of the above
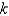 , is
, isA) 1/4 meter-Newton
B) 4 meter-Newtons
C) 1/4 Newton per meter
D) 16 Newtons per meter
E) none of the above

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
6
In the previous problem, the solution for the velocity, 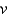 , is
, is
A)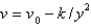
B)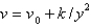
C)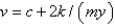
D)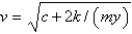
E) none of the above
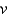 , is
, isA)
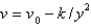
B)
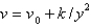
C)
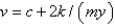
D)
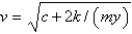
E) none of the above

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
7
In the previous two problems, how long does it take for the chain to fall completely to the ground?
A)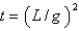
B)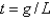
C)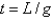
D)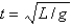
E)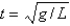
A)
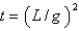
B)
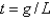
C)
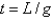
D)
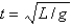
E)
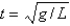

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
8
If the mass in the previous problem is pulled down two centimeters and released, the solution for the position is
A)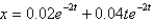
B)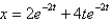
C)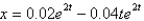
D)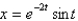
E)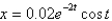
A)
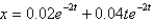
B)
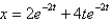
C)
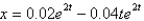
D)
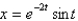
E)

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
9
In the previous problem, the function 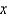 can be written as
can be written as
A)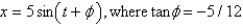
B)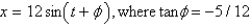
C)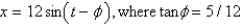
D)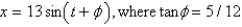
E)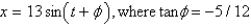
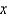 can be written as
can be written asA)
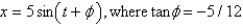
B)
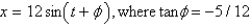
C)
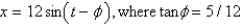
D)
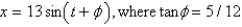
E)
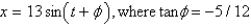

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
10
The initial value problem 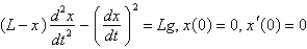 is a model of a chain of length
is a model of a chain of length 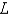 falling to the ground, where
falling to the ground, where 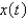 represents the length of chain on the ground at time
represents the length of chain on the ground at time 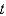 . The solution for
. The solution for 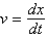 in terms of
in terms of 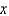 is
is
A)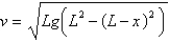
B)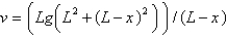
C)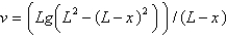
D)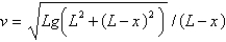
E)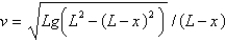
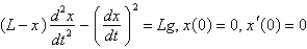 is a model of a chain of length
is a model of a chain of length 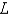 falling to the ground, where
falling to the ground, where 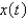 represents the length of chain on the ground at time
represents the length of chain on the ground at time 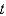 . The solution for
. The solution for 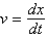 in terms of
in terms of 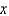 is
isA)
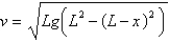
B)
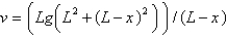
C)
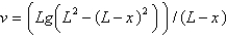
D)
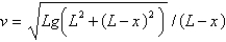
E)
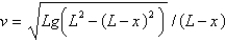

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
11
In the previous problem, if the mass is set in motion, the natural frequency, 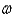 , is
, is
A)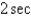
B)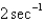
C)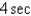
D)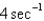
E)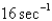
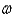 , is
, isA)
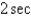
B)
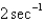
C)
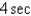
D)
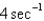
E)
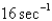

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
12
The differential equation 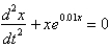 is a model for an undamped spring-mass system with a nonlinear restoring force. The initial conditions are
is a model for an undamped spring-mass system with a nonlinear restoring force. The initial conditions are 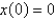 ,
, 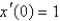 . The solution of the linearized system is
. The solution of the linearized system is
A)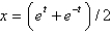
B)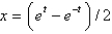
C)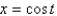
D)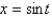
E)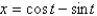
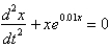 is a model for an undamped spring-mass system with a nonlinear restoring force. The initial conditions are
is a model for an undamped spring-mass system with a nonlinear restoring force. The initial conditions are 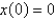 ,
, 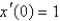 . The solution of the linearized system is
. The solution of the linearized system isA)
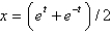
B)
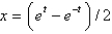
C)
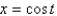
D)
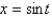
E)
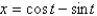

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
13
In the previous problem, the solution for 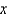 as a function of
as a function of 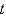 is
is
A)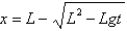
B)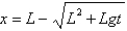
C)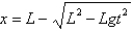
D)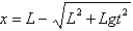
E)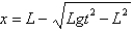
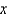 as a function of
as a function of 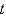 is
isA)
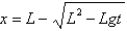
B)
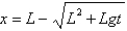
C)
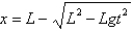
D)
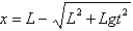
E)
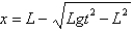

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
14
The solution of the boundary value problem in the previous problem is
A)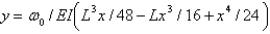
B)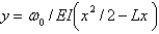
C)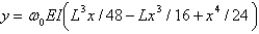
D)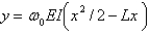
E) none of the above
A)
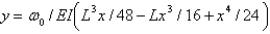
B)
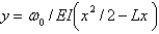
C)
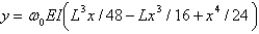
D)
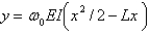
E) none of the above

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
15
A pendulum of length 16 feet hangs from the ceiling. Let 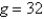 represent the gravitational acceleration. The correct linearized differential equation for the angle,
represent the gravitational acceleration. The correct linearized differential equation for the angle, 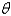 , that the swinging pendulum makes with the vertical is
, that the swinging pendulum makes with the vertical is
A)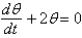
B)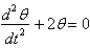
C)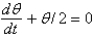
D)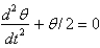
E)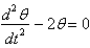
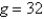 represent the gravitational acceleration. The correct linearized differential equation for the angle,
represent the gravitational acceleration. The correct linearized differential equation for the angle, 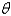 , that the swinging pendulum makes with the vertical is
, that the swinging pendulum makes with the vertical isA)
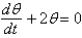
B)
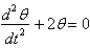
C)
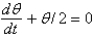
D)
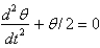
E)
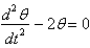

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
16
The boundary value problem 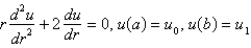 is a model for the temperature distribution between two concentric spheres of radii
is a model for the temperature distribution between two concentric spheres of radii 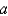 and
and 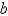 , with
, with 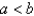 .The solution of this problem is
.The solution of this problem is
A)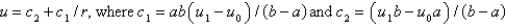
B)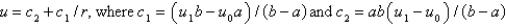
C)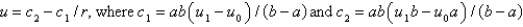
D)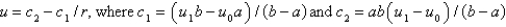
E) none of the above
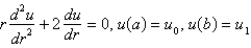 is a model for the temperature distribution between two concentric spheres of radii
is a model for the temperature distribution between two concentric spheres of radii 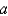 and
and 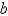 , with
, with 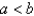 .The solution of this problem is
.The solution of this problem isA)
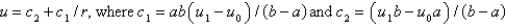
B)
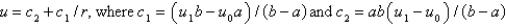
C)
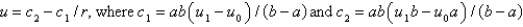
D)
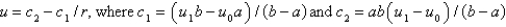
E) none of the above

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
17
In the previous two problems, if the mass is set into motion in a medium that imparts a damping force numerically equal to 16 times the velocity, the correct differential equation for the position, 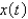 , of the mass at a function of time,
, of the mass at a function of time, 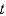 , is
, is
A)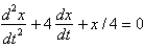
B)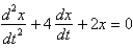
C)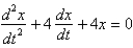
D)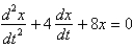
E)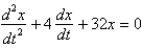
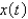 , of the mass at a function of time,
, of the mass at a function of time, 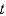 , is
, isA)
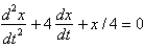
B)
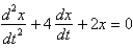
C)
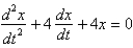
D)
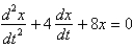
E)
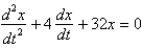

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
18
The solution of a vibrating spring problem is 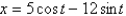 . The amplitude is
. The amplitude is
A) 1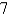
B)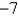
C) 7
D) 13
E) 60
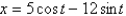 . The amplitude is
. The amplitude isA) 1
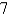
B)
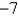
C) 7
D) 13
E) 60

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
19
In the previous problem, if 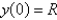 , the escape velocity is
, the escape velocity is
A)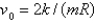
B)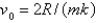
C)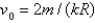
D)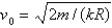
E) none of the above
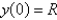 , the escape velocity is
, the escape velocity isA)
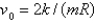
B)
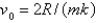
C)
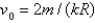
D)
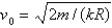
E) none of the above

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
20
The solution of the differential equation of the previous problem is
A)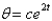
B)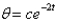
C)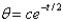
D)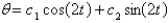
E)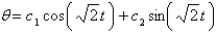
A)
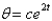
B)
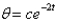
C)
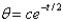
D)
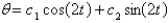
E)
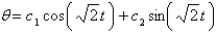

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
21
The boundary value problem 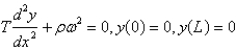 is a model of the shape of a rotating string. Suppose
is a model of the shape of a rotating string. Suppose 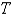 and
and 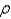 are constants. The critical angular rotation speed
are constants. The critical angular rotation speed 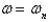 , for which there exist non-trivial solutions are
, for which there exist non-trivial solutions are
A)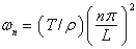
B)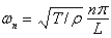
C)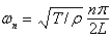
D)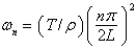
E)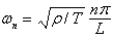
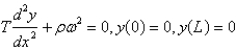 is a model of the shape of a rotating string. Suppose
is a model of the shape of a rotating string. Suppose 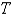 and
and 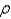 are constants. The critical angular rotation speed
are constants. The critical angular rotation speed 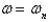 , for which there exist non-trivial solutions are
, for which there exist non-trivial solutions areA)
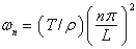
B)
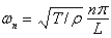
C)
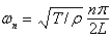
D)
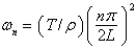
E)
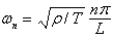

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
22
The moment of inertia of a cross section of a beam is 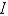 , and the Young's modulus is
, and the Young's modulus is 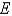 . Its flexural rigidity is
. Its flexural rigidity is
A)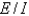
B)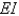
C)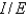
D)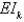 , where
, where 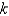 is the curvature
is the curvature
E)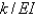 , where
, where 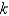 is the curvature
is the curvature
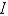 , and the Young's modulus is
, and the Young's modulus is 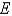 . Its flexural rigidity is
. Its flexural rigidity isA)
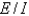
B)
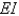
C)
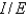
D)
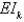 , where
, where 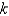 is the curvature
is the curvatureE)
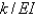 , where
, where 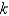 is the curvature
is the curvature
Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
23
In the previous problem, the solution for the velocity, 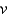 , is
, is
A)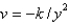
B)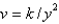
C)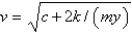
D)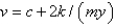
E) none of the above
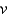 , is
, isA)
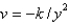
B)
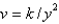
C)
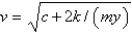
D)
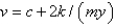
E) none of the above

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
24
The eigenvalue problem 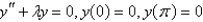 has the solution
has the solution
A)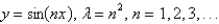
B)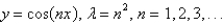
C)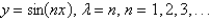
D)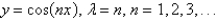
E) none of the above
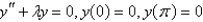 has the solution
has the solutionA)
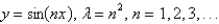
B)
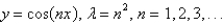
C)
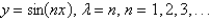
D)
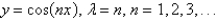
E) none of the above

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
25
The solution of the differential equation of the previous problem is
A)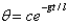
B)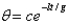
C)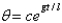
D)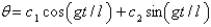
E)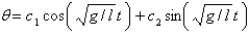
A)
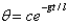
B)
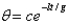
C)
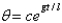
D)
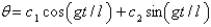
E)

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
26
A spring attached to the ceiling is stretched one foot by a four pound weight. The value of the Hooke's Law spring constant, 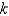 , is
, is
A) 4 pounds per foot
B) 1/4 pound per foot
C) 1/4 foot-pound
D) 4 foot-pounds
E) none of the above
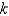 , is
, isA) 4 pounds per foot
B) 1/4 pound per foot
C) 1/4 foot-pound
D) 4 foot-pounds
E) none of the above

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
27
The solution of the problem given in the previous problem is
A)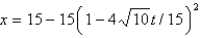
B)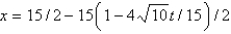
C)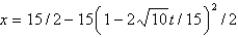
D)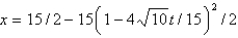
E)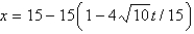
A)
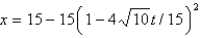
B)
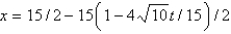
C)
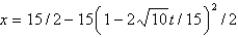
D)
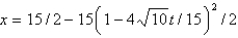
E)

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
28
In the previous problem the corresponding non-trivial solutions for 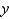 are
are
A)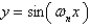
B)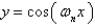
C)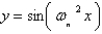
D)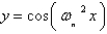
E) none of the above
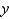 are
areA)
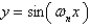
B)
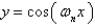
C)
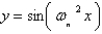
D)
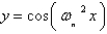
E) none of the above

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
29
A pendulum of length 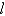 hangs from the ceiling. Let
hangs from the ceiling. Let 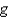 represent the gravitational acceleration. The correct linearized differential equation for the angle,
represent the gravitational acceleration. The correct linearized differential equation for the angle, 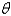 , that the swinging pendulum makes with the vertical is
, that the swinging pendulum makes with the vertical is
A)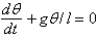
B)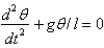
C)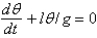
D)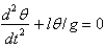
E)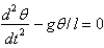
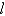 hangs from the ceiling. Let
hangs from the ceiling. Let 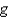 represent the gravitational acceleration. The correct linearized differential equation for the angle,
represent the gravitational acceleration. The correct linearized differential equation for the angle, 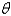 , that the swinging pendulum makes with the vertical is
, that the swinging pendulum makes with the vertical isA)
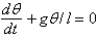
B)
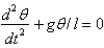
C)
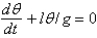
D)
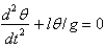
E)
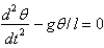

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
30
A beam of length 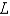 is simply supported at one end and free at the other end. The weight density is constant,
is simply supported at one end and free at the other end. The weight density is constant, 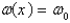 . Let
. Let 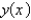 represent the deflection at point
represent the deflection at point 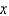 . The correct form of the boundary value problem for this beam is
. The correct form of the boundary value problem for this beam is
A)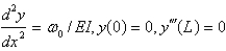
B)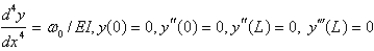
C)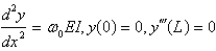
D)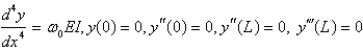
E) none of the above
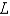 is simply supported at one end and free at the other end. The weight density is constant,
is simply supported at one end and free at the other end. The weight density is constant, 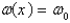 . Let
. Let 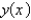 represent the deflection at point
represent the deflection at point 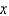 . The correct form of the boundary value problem for this beam is
. The correct form of the boundary value problem for this beam isA)
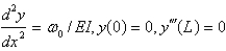
B)
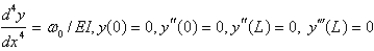
C)
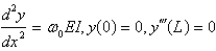
D)
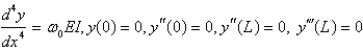
E) none of the above

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
31
The differential equation 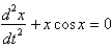 is a model for an undamped spring-mass system with a nonlinear forcing function. The initial conditions are
is a model for an undamped spring-mass system with a nonlinear forcing function. The initial conditions are 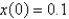 ,
, 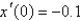 . The solution of the linearized system is
. The solution of the linearized system is
A)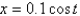
B)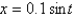
C)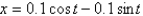
D)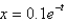
E)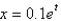
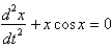 is a model for an undamped spring-mass system with a nonlinear forcing function. The initial conditions are
is a model for an undamped spring-mass system with a nonlinear forcing function. The initial conditions are 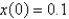 ,
, 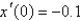 . The solution of the linearized system is
. The solution of the linearized system isA)
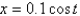
B)
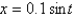
C)
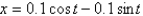
D)
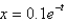
E)
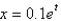

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
32
In the previous problem, if the mass is set in motion, the natural frequency, 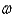 ,is
,is
A)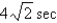
B)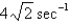
C)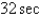
D)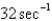
E)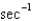
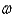 ,is
,isA)
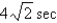
B)
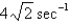
C)
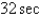
D)
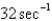
E)
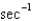

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
33
The solution of a vibrating spring problem is 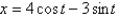 . The amplitude is
. The amplitude is
A)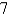
B)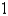
C)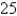
D)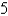
E)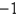
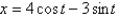 . The amplitude is
. The amplitude isA)
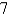
B)
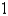
C)
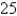
D)
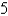
E)
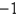

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
34
The eigenvalue problem 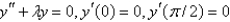 has the solution
has the solution
A)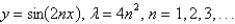
B)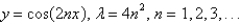
C)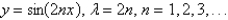
D)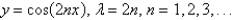
E) none of the above
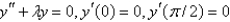 has the solution
has the solutionA)
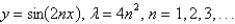
B)
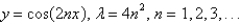
C)
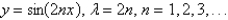
D)
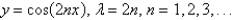
E) none of the above

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
35
In the previous problem, the function 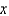 can be written as
can be written as
A)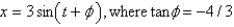
B)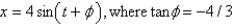
C)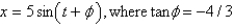
D)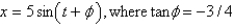
E)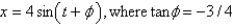
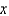 can be written as
can be written asA)
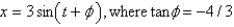
B)
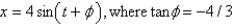
C)
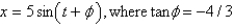
D)
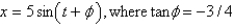
E)

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
36
In the previous two problems, the correct differential equation for the position, 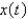 , of the mass at a function of time,
, of the mass at a function of time, 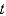 ,is
,is
A)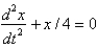
B)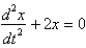
C)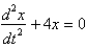
D)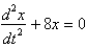
E)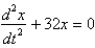
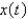 , of the mass at a function of time,
, of the mass at a function of time, 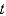 ,is
,isA)
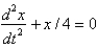
B)
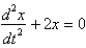
C)
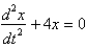
D)
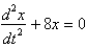
E)
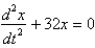

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
37
A rocket with mass 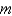 is launched vertically upward from the surface of the earth with a velocity
is launched vertically upward from the surface of the earth with a velocity 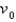 . Let
. Let 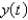 be the distance of the rocket from the center of the earth at time
be the distance of the rocket from the center of the earth at time 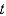 . Assuming that the only force acting on the rocket is gravity, which is inversely proportional to the square of the distance from the center of the earth, the correct differential equation for the position of the rocket is
. Assuming that the only force acting on the rocket is gravity, which is inversely proportional to the square of the distance from the center of the earth, the correct differential equation for the position of the rocket is
A)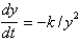
B)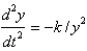
C)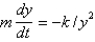
D)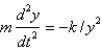
E) none of the above
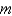 is launched vertically upward from the surface of the earth with a velocity
is launched vertically upward from the surface of the earth with a velocity 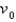 . Let
. Let 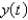 be the distance of the rocket from the center of the earth at time
be the distance of the rocket from the center of the earth at time 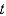 . Assuming that the only force acting on the rocket is gravity, which is inversely proportional to the square of the distance from the center of the earth, the correct differential equation for the position of the rocket is
. Assuming that the only force acting on the rocket is gravity, which is inversely proportional to the square of the distance from the center of the earth, the correct differential equation for the position of the rocket isA)
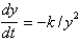
B)
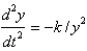
C)
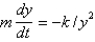
D)
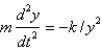
E) none of the above

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
38
In the previous problem, if 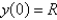 , what is the escape velocity?
, what is the escape velocity?
A)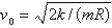
B)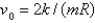
C)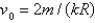
D)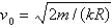
E) none of the above
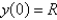 , what is the escape velocity?
, what is the escape velocity?A)
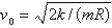
B)
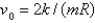
C)
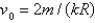
D)
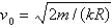
E) none of the above

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
39
If the mass in the previous problem is pulled down two feet and released, the solution for the position is
A)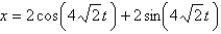
B)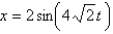
C)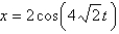
D)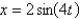
E)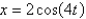
A)
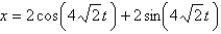
B)
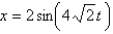
C)
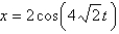
D)
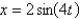
E)
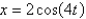

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
40
A 10 foot chain of weight density 2 pounds per foot is coiled on the ground. One end is pulled upward by a force of 10 pounds. The correct differential equation for the height, 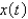 , of the end of the chain above the ground at time
, of the end of the chain above the ground at time 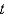 is
is
A)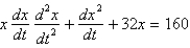
B)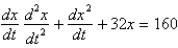
C)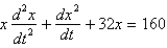
D)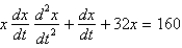
E)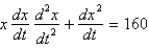
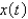 , of the end of the chain above the ground at time
, of the end of the chain above the ground at time 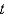 is
isA)
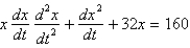
B)
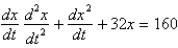
C)
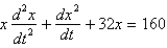
D)
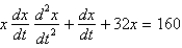
E)
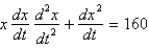

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck


