Deck 3: Applications of Differentiation
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/153
Play
Full screen (f)
Deck 3: Applications of Differentiation
1
Find the most general antiderivative of the function. 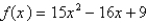
A)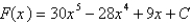
B)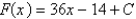
C)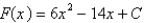
D)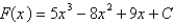
E)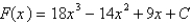
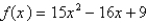
A)
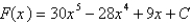
B)
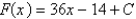
C)
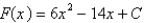
D)
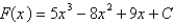
E)
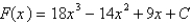
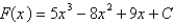
2
Find f.
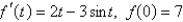
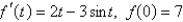
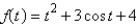
3
A particle moves along a straight line with velocity function 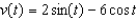 and its initial displacement is
and its initial displacement is 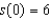 . Find its position function.
. Find its position function.
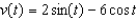 and its initial displacement is
and its initial displacement is 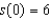 . Find its position function.
. Find its position function.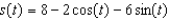
4
A company estimates that the marginal cost (in dollars per item) of producing items is 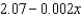 . If the cost of producing one item is $560 find the cost of producing 400 items.
. If the cost of producing one item is $560 find the cost of producing 400 items.
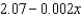 . If the cost of producing one item is $560 find the cost of producing 400 items.
. If the cost of producing one item is $560 find the cost of producing 400 items.
Unlock Deck
Unlock for access to all 153 flashcards in this deck.
Unlock Deck
k this deck
5
Find the most general antiderivative of the function. 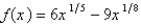
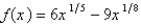

Unlock Deck
Unlock for access to all 153 flashcards in this deck.
Unlock Deck
k this deck
6
Find the most general antiderivative of the function. 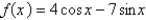
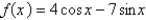

Unlock Deck
Unlock for access to all 153 flashcards in this deck.
Unlock Deck
k this deck
7
A ballast is dropped from a stationary hot-air balloon that is at an altitude of 256 ft. Find (a) an expression for the altitude of the ballast after t seconds, (b) the time when it strikes the ground, and (c) its velocity when it strikes the ground. (Disregard air resistance and take 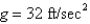 .)
.)
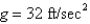 .)
.)
Unlock Deck
Unlock for access to all 153 flashcards in this deck.
Unlock Deck
k this deck
8
What constant acceleration is required to increase the speed of a car from 30 ft/s to 45 ft/s in
4 s?
4 s?

Unlock Deck
Unlock for access to all 153 flashcards in this deck.
Unlock Deck
k this deck
9
A car braked with a constant deceleration of 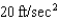 , producing skid marks measuring 500 ft before coming to a stop. How fast was the car traveling when the brakes were first applied?
, producing skid marks measuring 500 ft before coming to a stop. How fast was the car traveling when the brakes were first applied?
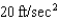 , producing skid marks measuring 500 ft before coming to a stop. How fast was the car traveling when the brakes were first applied?
, producing skid marks measuring 500 ft before coming to a stop. How fast was the car traveling when the brakes were first applied?
Unlock Deck
Unlock for access to all 153 flashcards in this deck.
Unlock Deck
k this deck
10
To what constant deceleration would a car moving along a straight road be subjected if the car were brought to rest from a speed of 86 ft/sec in 7 sec? What would the stopping distance be?

Unlock Deck
Unlock for access to all 153 flashcards in this deck.
Unlock Deck
k this deck
11
Given that the graph of f passes through the point (4, 69) and that the slope of its tangent line at 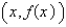 is
is 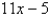 , find f (1) .
, find f (1) .
A)11
B)1
C)0
D)12
E)6
 is
is 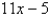 , find f (1) .
, find f (1) .A)11
B)1
C)0
D)12
E)6

Unlock Deck
Unlock for access to all 153 flashcards in this deck.
Unlock Deck
k this deck
12
Estimate the value of 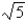 by using three iterations of Newton's method to solve the equation
by using three iterations of Newton's method to solve the equation 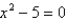 with initial estimate
with initial estimate 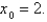 Round your final estimate to four decimal places.
Round your final estimate to four decimal places.
A)1.71
B)2.2662
C)2.2361
D)1.6535
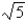 by using three iterations of Newton's method to solve the equation
by using three iterations of Newton's method to solve the equation 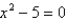 with initial estimate
with initial estimate 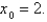 Round your final estimate to four decimal places.
Round your final estimate to four decimal places.A)1.71
B)2.2662
C)2.2361
D)1.6535

Unlock Deck
Unlock for access to all 153 flashcards in this deck.
Unlock Deck
k this deck
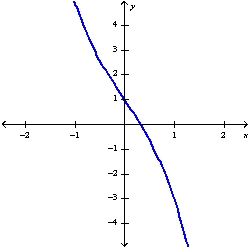
13
Suppose the line 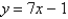 is tangent to the curve
is tangent to the curve 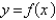 when
when 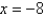 . If Newton's method is used to locate a root of the equation
. If Newton's method is used to locate a root of the equation 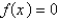 and the initial approximation is
and the initial approximation is 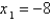 , find the second approximation
, find the second approximation 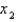 .
.
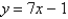 is tangent to the curve
is tangent to the curve 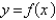 when
when 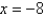 . If Newton's method is used to locate a root of the equation
. If Newton's method is used to locate a root of the equation 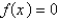 and the initial approximation is
and the initial approximation is 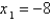 , find the second approximation
, find the second approximation 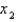 .
.
Unlock Deck
Unlock for access to all 153 flashcards in this deck.
Unlock Deck
k this deck
14
Evaluate 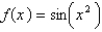 , and tell whether its antiderivative F is increasing or decreasing at the point
, and tell whether its antiderivative F is increasing or decreasing at the point 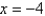 radians.
radians.
A)-0.288, increasing
B)0.757, increasing
C) -0.757, decreasing
D)0.277, decreasing
E)0.757, decreasing
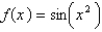 , and tell whether its antiderivative F is increasing or decreasing at the point
, and tell whether its antiderivative F is increasing or decreasing at the point 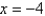 radians.
radians.A)-0.288, increasing
B)0.757, increasing
C) -0.757, decreasing
D)0.277, decreasing
E)0.757, decreasing

Unlock Deck
Unlock for access to all 153 flashcards in this deck.
Unlock Deck
k this deck
15
Use Newton's method to approximate the zero of 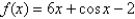 between
between 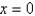 and
and 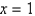 using
using 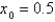 . Continue until two successive approximations differ by less than 0.00001.
. Continue until two successive approximations differ by less than 0.00001.
A)0.16904
B)0.11154
C)0.23624
D)0.07984
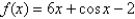 between
between 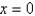 and
and 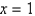 using
using 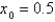 . Continue until two successive approximations differ by less than 0.00001.
. Continue until two successive approximations differ by less than 0.00001.A)0.16904
B)0.11154
C)0.23624
D)0.07984

Unlock Deck
Unlock for access to all 153 flashcards in this deck.
Unlock Deck
k this deck
16
Use Newton's method to approximate the indicated root of 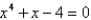 in the interval
in the interval 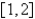 , correct to six decimal places.
, correct to six decimal places.
Use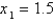 as the initial approximation.
as the initial approximation.
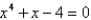 in the interval
in the interval 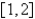 , correct to six decimal places.
, correct to six decimal places.Use
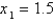 as the initial approximation.
as the initial approximation.
Unlock Deck
Unlock for access to all 153 flashcards in this deck.
Unlock Deck
k this deck
17
The size of the monthly repayment k that amortizes a loan of A dollars in N years at an interest rate of r per year, compounded monthly, on the unpaid balance is given by 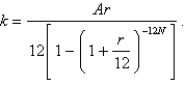 The value of r can be found by performing the iteration
The value of r can be found by performing the iteration 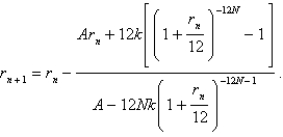 A family secured a loan of $360,000 from a bank to finance the purchase of a house. They have agreed to repay the loan in equal monthly installments of $2476 over 25 years. Find the interest rate on this loan. Round the rate to one decimal place.
A family secured a loan of $360,000 from a bank to finance the purchase of a house. They have agreed to repay the loan in equal monthly installments of $2476 over 25 years. Find the interest rate on this loan. Round the rate to one decimal place.
A)8.7%
B)7.7%
C)6.7%
D)5.7%
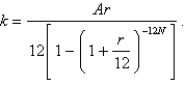 The value of r can be found by performing the iteration
The value of r can be found by performing the iteration 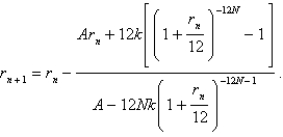 A family secured a loan of $360,000 from a bank to finance the purchase of a house. They have agreed to repay the loan in equal monthly installments of $2476 over 25 years. Find the interest rate on this loan. Round the rate to one decimal place.
A family secured a loan of $360,000 from a bank to finance the purchase of a house. They have agreed to repay the loan in equal monthly installments of $2476 over 25 years. Find the interest rate on this loan. Round the rate to one decimal place.A)8.7%
B)7.7%
C)6.7%
D)5.7%

Unlock Deck
Unlock for access to all 153 flashcards in this deck.
Unlock Deck
k this deck
18
Find the position function of a particle moving along a coordinate line that satisfies the given condition. 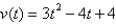 , s(1) = -1
, s(1) = -1
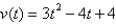 , s(1) = -1
, s(1) = -1
Unlock Deck
Unlock for access to all 153 flashcards in this deck.
Unlock Deck
k this deck
19
Use Newton's method with the specified initial approximation 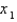 to find
to find 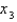 , the third approximation to the root of the given equation. (Give your answer to four decimal places.)
, the third approximation to the root of the given equation. (Give your answer to four decimal places.) 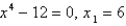
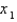 to find
to find 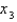 , the third approximation to the root of the given equation. (Give your answer to four decimal places.)
, the third approximation to the root of the given equation. (Give your answer to four decimal places.) 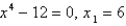

Unlock Deck
Unlock for access to all 153 flashcards in this deck.
Unlock Deck
k this deck
20
Find the position function of a particle moving along a coordinate line that satisfies the given conditions. 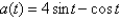 , s(0) = 5, v(0) = 0
, s(0) = 5, v(0) = 0
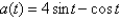 , s(0) = 5, v(0) = 0
, s(0) = 5, v(0) = 0
Unlock Deck
Unlock for access to all 153 flashcards in this deck.
Unlock Deck
k this deck
21
Use Newton's method to find the point of intersection of the graphs of 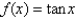 and
and 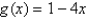 to within 0.00001 by solving the equation
to within 0.00001 by solving the equation 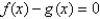 using
using 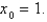
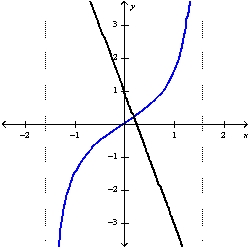
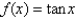 and
and 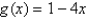 to within 0.00001 by solving the equation
to within 0.00001 by solving the equation 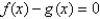 using
using 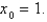


Unlock Deck
Unlock for access to all 153 flashcards in this deck.
Unlock Deck
k this deck
22
What is the shortest possible length of the line segment that is cut off by the first quadrant and is tangent to the curve 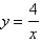 at some point?
at some point?
A)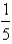
B)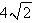
C)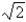
D)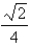
E)None of these
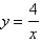 at some point?
at some point?A)
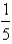
B)
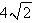
C)
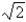
D)
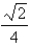
E)None of these

Unlock Deck
Unlock for access to all 153 flashcards in this deck.
Unlock Deck
k this deck
23
A woman at a point A on the shore of a circular lake with radius 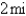 wants to arrive at the point C diametrically opposite on the other side of the lake in the shortest possible time. She can walk at the rate of
wants to arrive at the point C diametrically opposite on the other side of the lake in the shortest possible time. She can walk at the rate of 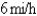 and row a boat at
and row a boat at 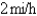 . How should she proceed? (Find
. How should she proceed? (Find 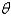 ). Round the result, if necessary, to the nearest hundredth.
). Round the result, if necessary, to the nearest hundredth. 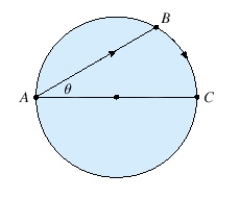
A)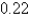 radians
radians
B)She should walk around the lake from point A to point C.
C)She should row from point A to point C radians
D)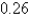 radians
radians
E)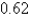 radians
radians
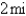 wants to arrive at the point C diametrically opposite on the other side of the lake in the shortest possible time. She can walk at the rate of
wants to arrive at the point C diametrically opposite on the other side of the lake in the shortest possible time. She can walk at the rate of 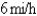 and row a boat at
and row a boat at 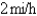 . How should she proceed? (Find
. How should she proceed? (Find 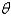 ). Round the result, if necessary, to the nearest hundredth.
). Round the result, if necessary, to the nearest hundredth. 
A)
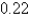 radians
radiansB)She should walk around the lake from point A to point C.
C)She should row from point A to point C radians
D)
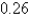 radians
radiansE)
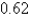 radians
radians
Unlock Deck
Unlock for access to all 153 flashcards in this deck.
Unlock Deck
k this deck
24
Find the smallest possible area of an isosceles triangle that is circumscribed about a circle of radius 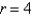 .
.
A)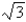
B)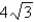
C)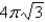
D)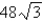
E)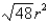
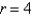 .
.A)
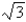
B)
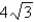
C)
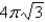
D)
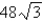
E)
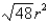

Unlock Deck
Unlock for access to all 153 flashcards in this deck.
Unlock Deck
k this deck
25
The sum of two positive numbers is 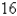 . What is the smallest possible value of the sum of their squares?
. What is the smallest possible value of the sum of their squares?
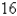 . What is the smallest possible value of the sum of their squares?
. What is the smallest possible value of the sum of their squares?
Unlock Deck
Unlock for access to all 153 flashcards in this deck.
Unlock Deck
k this deck
26
Find two positive numbers whose product is 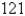 and whose sum is a minimum.
and whose sum is a minimum.
A)2, 72
B)3, 48
C)6, 24
D)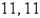
E)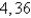
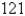 and whose sum is a minimum.
and whose sum is a minimum.A)2, 72
B)3, 48
C)6, 24
D)
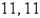
E)
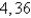

Unlock Deck
Unlock for access to all 153 flashcards in this deck.
Unlock Deck
k this deck
27
Consider the following problem: A farmer with 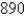 ft of fencing wants to enclose a rectangular area and then divide it into four pens with fencing parallel to one side of the rectangle. What is the largest possible total area of the four pens?
ft of fencing wants to enclose a rectangular area and then divide it into four pens with fencing parallel to one side of the rectangle. What is the largest possible total area of the four pens?
A)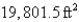
B)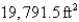
C)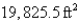
D)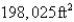
E)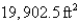
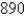 ft of fencing wants to enclose a rectangular area and then divide it into four pens with fencing parallel to one side of the rectangle. What is the largest possible total area of the four pens?
ft of fencing wants to enclose a rectangular area and then divide it into four pens with fencing parallel to one side of the rectangle. What is the largest possible total area of the four pens?A)
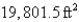
B)
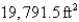
C)
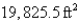
D)
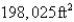
E)
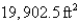

Unlock Deck
Unlock for access to all 153 flashcards in this deck.
Unlock Deck
k this deck
28
A manufacturer has been selling 1,200 television sets a week at $400 each. A market survey indicates that for each $30 rebate offered to the buyer, the number of sets sold will increase by 60 per week. Find the demand function.
A)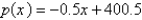
B)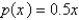
C)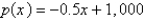
D)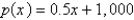
E)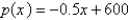
A)
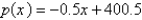
B)
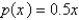
C)
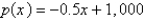
D)
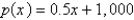
E)
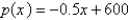

Unlock Deck
Unlock for access to all 153 flashcards in this deck.
Unlock Deck
k this deck
29
A rectangular beam will be cut from a cylindrical log of radius 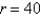 inches. Suppose that the strength of a rectangular beam is proportional to the product of its width and the square of its depth. Find the dimensions of the strongest beam that can be cut from the cylindrical log.
inches. Suppose that the strength of a rectangular beam is proportional to the product of its width and the square of its depth. Find the dimensions of the strongest beam that can be cut from the cylindrical log. 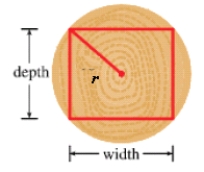
A)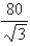 in,
in, 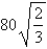 in
in
B)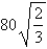 in,
in, 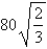 in
in
C)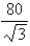 in,
in, 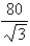 in
in
D)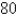 in,
in, 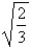 in
in
E)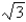 in,
in, 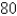 in
in
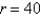 inches. Suppose that the strength of a rectangular beam is proportional to the product of its width and the square of its depth. Find the dimensions of the strongest beam that can be cut from the cylindrical log.
inches. Suppose that the strength of a rectangular beam is proportional to the product of its width and the square of its depth. Find the dimensions of the strongest beam that can be cut from the cylindrical log. 
A)
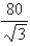 in,
in, 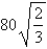 in
inB)
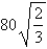 in,
in, 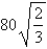 in
inC)
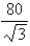 in,
in, 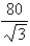 in
inD)
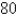 in,
in, 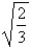 in
inE)
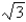 in,
in, 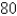 in
in
Unlock Deck
Unlock for access to all 153 flashcards in this deck.
Unlock Deck
k this deck
30
A production editor decided that a promotional flyer should have a 1-in. margin at the top and the bottom, and a 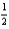 -in. margin on each side. The editor further stipulated that the flyer should have an area of 288
-in. margin on each side. The editor further stipulated that the flyer should have an area of 288 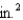 . Determine the dimensions of the flyer that will result in the maximum printed area on the flyer.
. Determine the dimensions of the flyer that will result in the maximum printed area on the flyer. 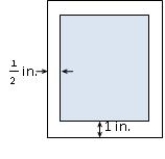
A)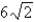 in.
in. 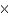
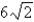 in.
in.
B)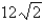 in.
in. 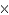
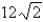 in.
in.
C)12 in.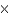 24 in.
24 in.
D)6 in.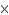 48 in.
48 in.
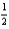 -in. margin on each side. The editor further stipulated that the flyer should have an area of 288
-in. margin on each side. The editor further stipulated that the flyer should have an area of 288 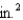 . Determine the dimensions of the flyer that will result in the maximum printed area on the flyer.
. Determine the dimensions of the flyer that will result in the maximum printed area on the flyer. 
A)
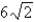 in.
in. 
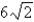 in.
in.B)
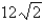 in.
in. 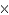
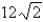 in.
in.C)12 in.
 24 in.
24 in.D)6 in.
 48 in.
48 in.
Unlock Deck
Unlock for access to all 153 flashcards in this deck.
Unlock Deck
k this deck
31
Use Newton's method to approximate the zero of 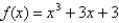 between
between 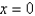 and
and 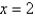 using
using 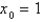 . Continue until two successive approximations differ by less than 0.00001.
. Continue until two successive approximations differ by less than 0.00001.
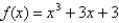 between
between 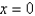 and
and 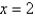 using
using 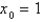 . Continue until two successive approximations differ by less than 0.00001.
. Continue until two successive approximations differ by less than 0.00001.
Unlock Deck
Unlock for access to all 153 flashcards in this deck.
Unlock Deck
k this deck
32
A piece of wire 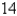 m long is cut into two pieces. One piece is bent into a square and the other is bent into an equilateral triangle. How should the wire be cut for the square so that the total area enclosed is a minimum? Round your answer to the nearest hundredth.
m long is cut into two pieces. One piece is bent into a square and the other is bent into an equilateral triangle. How should the wire be cut for the square so that the total area enclosed is a minimum? Round your answer to the nearest hundredth.
A)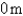
B)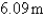
C)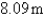
D)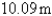
E)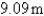
 m long is cut into two pieces. One piece is bent into a square and the other is bent into an equilateral triangle. How should the wire be cut for the square so that the total area enclosed is a minimum? Round your answer to the nearest hundredth.
m long is cut into two pieces. One piece is bent into a square and the other is bent into an equilateral triangle. How should the wire be cut for the square so that the total area enclosed is a minimum? Round your answer to the nearest hundredth.A)
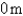
B)
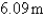
C)
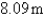
D)
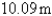
E)
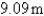

Unlock Deck
Unlock for access to all 153 flashcards in this deck.
Unlock Deck
k this deck
33
Approximate the zero of 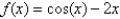 in
in 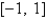 to within 0.00001.
to within 0.00001.
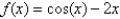 in
in 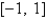 to within 0.00001.
to within 0.00001.
Unlock Deck
Unlock for access to all 153 flashcards in this deck.
Unlock Deck
k this deck
34
Use Newton's method to find the zero of 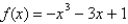 to within 0.00001 by solving the equation
to within 0.00001 by solving the equation 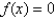 using
using 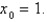
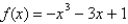 to within 0.00001 by solving the equation
to within 0.00001 by solving the equation 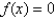 using
using 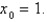


Unlock Deck
Unlock for access to all 153 flashcards in this deck.
Unlock Deck
k this deck
35
Approximate the zero of 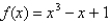 in
in 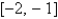 to within 0.00001.
to within 0.00001.
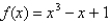 in
in 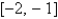 to within 0.00001.
to within 0.00001.
Unlock Deck
Unlock for access to all 153 flashcards in this deck.
Unlock Deck
k this deck
36
A right circular cylinder is inscribed in a sphere of radius 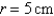 . Find the largest possible surface area of such a cylinder. Round the result to the nearest hundredth.
. Find the largest possible surface area of such a cylinder. Round the result to the nearest hundredth.
A)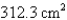
B)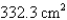
C)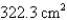
D)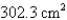
E)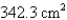
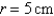 . Find the largest possible surface area of such a cylinder. Round the result to the nearest hundredth.
. Find the largest possible surface area of such a cylinder. Round the result to the nearest hundredth.A)
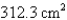
B)
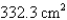
C)
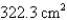
D)
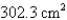
E)
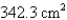

Unlock Deck
Unlock for access to all 153 flashcards in this deck.
Unlock Deck
k this deck
37
The average cost of producing x units of a commodity is given by the equation 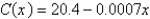 .
.
Find the marginal cost at a production level of 1,255 units.
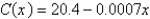 .
.Find the marginal cost at a production level of 1,255 units.

Unlock Deck
Unlock for access to all 153 flashcards in this deck.
Unlock Deck
k this deck
38
Find the dimensions of the rectangle enclosed in the semicircle 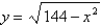 with the largest possible area.
with the largest possible area. 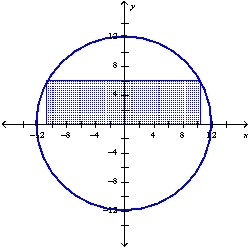
A)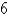 in.
in. 
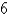 in.
in.
B)5 in. 7 in.
7 in.
C)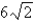 in.
in. 
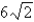 in.
in.
D)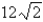 in.
in. 
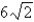 in.
in.
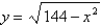 with the largest possible area.
with the largest possible area. 
A)
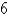 in.
in. 
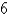 in.
in.B)5 in.
 7 in.
7 in.C)
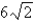 in.
in. 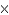
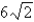 in.
in.D)
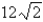 in.
in. 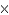
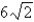 in.
in.
Unlock Deck
Unlock for access to all 153 flashcards in this deck.
Unlock Deck
k this deck
39
Find the dimensions of a rectangle of area 400 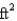 that has the smallest possible perimeter.
that has the smallest possible perimeter.
A)4 ft by 100 ft
B)1 ft by 400 ft
C)20 ft by 20 ft
D)2 ft by 200 ft
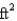 that has the smallest possible perimeter.
that has the smallest possible perimeter.A)4 ft by 100 ft
B)1 ft by 400 ft
C)20 ft by 20 ft
D)2 ft by 200 ft

Unlock Deck
Unlock for access to all 153 flashcards in this deck.
Unlock Deck
k this deck
40
Find the point on the line 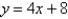 that is closest to the origin.
that is closest to the origin.
A)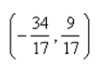
B)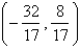
C)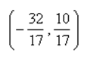
D)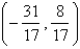
E)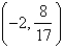
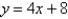 that is closest to the origin.
that is closest to the origin.A)
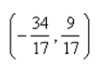
B)
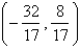
C)
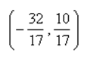
D)
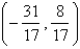
E)
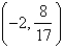

Unlock Deck
Unlock for access to all 153 flashcards in this deck.
Unlock Deck
k this deck
41
An aircraft manufacturer wants to determine the best selling price for a new airplane. The company estimates that the initial cost of designing the airplane and setting up the factories in which to build it will be 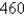 million dollars. The additional cost of manufacturing each plane can be modeled by the function
million dollars. The additional cost of manufacturing each plane can be modeled by the function 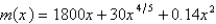 where x is the number of aircraft produced and m is the manufacturing cost, in millions of dollars. The company estimates that if it charges a price p (in millions of dollars) for each plane, it will be able to sell
where x is the number of aircraft produced and m is the manufacturing cost, in millions of dollars. The company estimates that if it charges a price p (in millions of dollars) for each plane, it will be able to sell 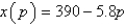 .
.
Find the cost function.
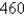 million dollars. The additional cost of manufacturing each plane can be modeled by the function
million dollars. The additional cost of manufacturing each plane can be modeled by the function 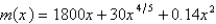 where x is the number of aircraft produced and m is the manufacturing cost, in millions of dollars. The company estimates that if it charges a price p (in millions of dollars) for each plane, it will be able to sell
where x is the number of aircraft produced and m is the manufacturing cost, in millions of dollars. The company estimates that if it charges a price p (in millions of dollars) for each plane, it will be able to sell 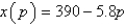 .
.Find the cost function.

Unlock Deck
Unlock for access to all 153 flashcards in this deck.
Unlock Deck
k this deck
42
The manager of a 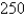 -unit apartment complex knows from experience that all units will be occupied if the rent is
-unit apartment complex knows from experience that all units will be occupied if the rent is 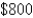 per month. A market survey suggests that, on the average, one additional unit will remain vacant for each
per month. A market survey suggests that, on the average, one additional unit will remain vacant for each 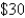 increase in rent. What rent should the manager charge to maximize revenue?
increase in rent. What rent should the manager charge to maximize revenue?
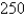 -unit apartment complex knows from experience that all units will be occupied if the rent is
-unit apartment complex knows from experience that all units will be occupied if the rent is 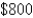 per month. A market survey suggests that, on the average, one additional unit will remain vacant for each
per month. A market survey suggests that, on the average, one additional unit will remain vacant for each 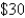 increase in rent. What rent should the manager charge to maximize revenue?
increase in rent. What rent should the manager charge to maximize revenue?
Unlock Deck
Unlock for access to all 153 flashcards in this deck.
Unlock Deck
k this deck
43
If 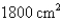 of material is available to make a box with a square base and an open top, find the largest possible volume of the box.
of material is available to make a box with a square base and an open top, find the largest possible volume of the box.
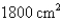 of material is available to make a box with a square base and an open top, find the largest possible volume of the box.
of material is available to make a box with a square base and an open top, find the largest possible volume of the box.
Unlock Deck
Unlock for access to all 153 flashcards in this deck.
Unlock Deck
k this deck
44
For what values of 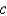 does the curve have maximum and minimum points for the given function
does the curve have maximum and minimum points for the given function 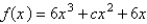 ?
?
A)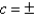
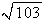
B)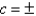
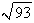
C)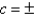
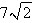
D)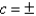
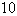
E)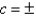
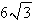
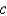 does the curve have maximum and minimum points for the given function
does the curve have maximum and minimum points for the given function 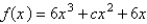 ?
?A)
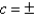
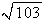
B)
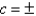
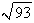
C)
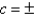
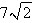
D)
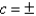
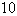
E)
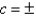
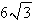

Unlock Deck
Unlock for access to all 153 flashcards in this deck.
Unlock Deck
k this deck
45
Find an equation of the line through the point 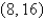 that cuts off the least area from the first quadrant.
that cuts off the least area from the first quadrant.
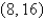 that cuts off the least area from the first quadrant.
that cuts off the least area from the first quadrant.
Unlock Deck
Unlock for access to all 153 flashcards in this deck.
Unlock Deck
k this deck
46
Find the maximum area of a rectangle that can be circumscribed about a given rectangle with length 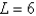 and width
and width 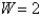 .
. 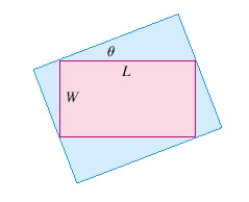
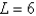 and width
and width 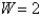 .
. 

Unlock Deck
Unlock for access to all 153 flashcards in this deck.
Unlock Deck
k this deck
47
What is the function of the graph? 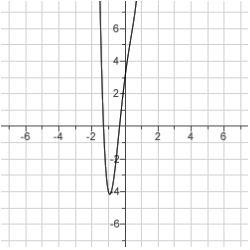
A)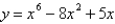
B)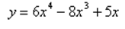
C)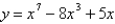
D)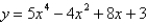
E)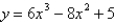

A)
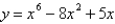
B)
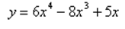
C)
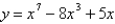
D)
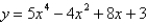
E)
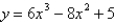

Unlock Deck
Unlock for access to all 153 flashcards in this deck.
Unlock Deck
k this deck
48
A woman is on a lake in a rowboat located one mile form the closest point P of a straight shoreline (see the figure). She wishes to get to point Q, 8 miles along the shore from P, by rowing to a point R between P and Q and then walking the rest of the distance. If she can row at a speed of 3 mph and walk at a speed of 4 mph, how should she pick the point R to get to Q as quickly as possible? How much time does she require?
 8 mi
8 mi 
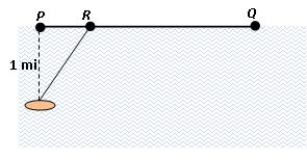
 8 mi
8 mi 


Unlock Deck
Unlock for access to all 153 flashcards in this deck.
Unlock Deck
k this deck
49
The owner of a ranch has 4000 yd of fencing with which to enclose a rectangular piece of grazing land situated along a straight portion of a river. If fencing is not required along the river, what are the dimensions of the largest area he can enclose? What is the area? 


Unlock Deck
Unlock for access to all 153 flashcards in this deck.
Unlock Deck
k this deck
50
A baseball team plays in a stadium that holds 56,000 spectators. With ticket prices at $9, the average attendance had been 32,000. When ticket prices were lowered to $8, the average attendance rose to 36,000. How should ticket prices be set to maximize revenue? Assume the demand function is linear.

Unlock Deck
Unlock for access to all 153 flashcards in this deck.
Unlock Deck
k this deck
51
For what values of 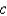 does the curve have maximum and minimum points for the given function
does the curve have maximum and minimum points for the given function 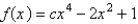 ? Select the correct answer.
? Select the correct answer.
A)For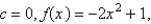 a parabola whose vertex
a parabola whose vertex 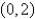 , is the absolute maximum.For
, is the absolute maximum.For 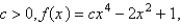 opens downward with one minimum points.For
opens downward with one minimum points.For 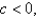 the graph opens upward, and has an absolute maximum at
the graph opens upward, and has an absolute maximum at 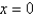 and no local minimum.
and no local minimum.
B)For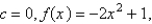 a parabola whose vertex
a parabola whose vertex 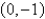 , is the absolute maximum.For
, is the absolute maximum.For 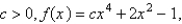 opens downward with two maximum points.For
opens downward with two maximum points.For 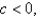 the graph opens upward, and has an absolute minimum at
the graph opens upward, and has an absolute minimum at 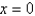 .
.
C)For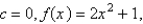 a parabola whose vertex
a parabola whose vertex 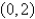 , is the absolute maximum.For
, is the absolute maximum.For 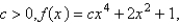 opens upward with two minimum points.For
opens upward with two minimum points.For 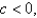 the graph opens downward, and has an absolute minimum at
the graph opens downward, and has an absolute minimum at 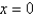 and no local minimum.
and no local minimum.
D)For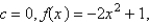 a parabola whose vertex
a parabola whose vertex 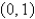 , is the absolute maximum.For
, is the absolute maximum.For 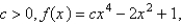 opens upward with two minimum points.For
opens upward with two minimum points.For 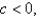 the graph opens downward, and has an absolute maximum at
the graph opens downward, and has an absolute maximum at 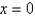 and no local minimum.
and no local minimum.
E)For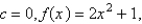 a parabola whose vertex
a parabola whose vertex 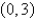 , is the absolute maximum.For
, is the absolute maximum.For 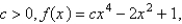 opens upward with two minimum points.For
opens upward with two minimum points.For 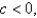 the graph opens downward, and has an absolute minimum at
the graph opens downward, and has an absolute minimum at 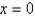 and no local minimum.
and no local minimum.
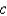 does the curve have maximum and minimum points for the given function
does the curve have maximum and minimum points for the given function 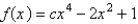 ? Select the correct answer.
? Select the correct answer.A)For
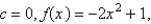 a parabola whose vertex
a parabola whose vertex 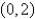 , is the absolute maximum.For
, is the absolute maximum.For 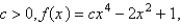 opens downward with one minimum points.For
opens downward with one minimum points.For 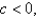 the graph opens upward, and has an absolute maximum at
the graph opens upward, and has an absolute maximum at 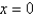 and no local minimum.
and no local minimum.B)For
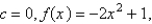 a parabola whose vertex
a parabola whose vertex 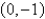 , is the absolute maximum.For
, is the absolute maximum.For 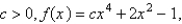 opens downward with two maximum points.For
opens downward with two maximum points.For 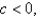 the graph opens upward, and has an absolute minimum at
the graph opens upward, and has an absolute minimum at 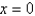 .
.C)For
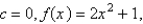 a parabola whose vertex
a parabola whose vertex 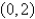 , is the absolute maximum.For
, is the absolute maximum.For 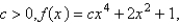 opens upward with two minimum points.For
opens upward with two minimum points.For 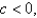 the graph opens downward, and has an absolute minimum at
the graph opens downward, and has an absolute minimum at 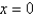 and no local minimum.
and no local minimum.D)For
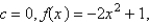 a parabola whose vertex
a parabola whose vertex 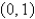 , is the absolute maximum.For
, is the absolute maximum.For 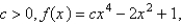 opens upward with two minimum points.For
opens upward with two minimum points.For 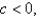 the graph opens downward, and has an absolute maximum at
the graph opens downward, and has an absolute maximum at 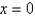 and no local minimum.
and no local minimum.E)For
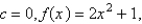 a parabola whose vertex
a parabola whose vertex 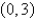 , is the absolute maximum.For
, is the absolute maximum.For 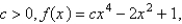 opens upward with two minimum points.For
opens upward with two minimum points.For 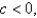 the graph opens downward, and has an absolute minimum at
the graph opens downward, and has an absolute minimum at 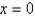 and no local minimum.
and no local minimum.
Unlock Deck
Unlock for access to all 153 flashcards in this deck.
Unlock Deck
k this deck
52
Select the correct graph for the given function 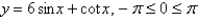 .
.
A)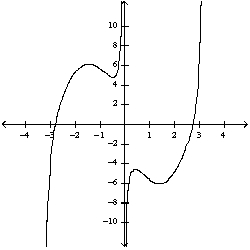
B)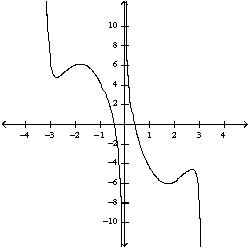
C)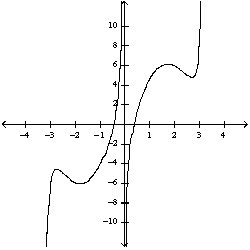
D)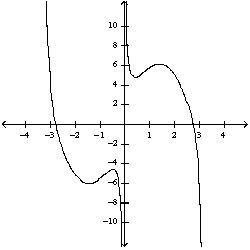
E)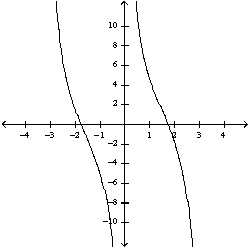
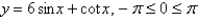 .
.A)

B)

C)

D)

E)


Unlock Deck
Unlock for access to all 153 flashcards in this deck.
Unlock Deck
k this deck
53
A Norman window has the shape of a rectangle surmounted by a semicircle. (Thus the diameter of the semicircle is equal to the width of the rectangle.) If the perimeter of the window is 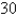 ft, find the dimensions of the window so that the greatest possible amount of light is admitted.
ft, find the dimensions of the window so that the greatest possible amount of light is admitted.
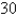 ft, find the dimensions of the window so that the greatest possible amount of light is admitted.
ft, find the dimensions of the window so that the greatest possible amount of light is admitted.
Unlock Deck
Unlock for access to all 153 flashcards in this deck.
Unlock Deck
k this deck
54
Find the point on the line 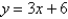 that is closest to the origin.
that is closest to the origin.
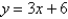 that is closest to the origin.
that is closest to the origin.
Unlock Deck
Unlock for access to all 153 flashcards in this deck.
Unlock Deck
k this deck
55
A rectangular box having a top and a square base is to be constructed at a cost of $1. If the material for the bottom costs $0.35 per square foot, the material for the top costs $0.15 per square foot, and the material for the sides costs $0.20 per square foot, find the dimensions and volume of the box of maximum volume that can be constructed.

Unlock Deck
Unlock for access to all 153 flashcards in this deck.
Unlock Deck
k this deck
56
What is the function of the graph? 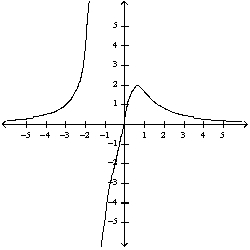
A)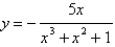
B)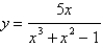
C)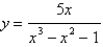
D)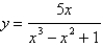
E)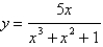

A)
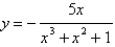
B)
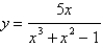
C)
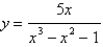
D)
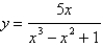
E)
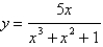

Unlock Deck
Unlock for access to all 153 flashcards in this deck.
Unlock Deck
k this deck
57
A steel pipe is being carried down a hallway 14 ft wide. At the end of the hall there is a right-angled turn into a narrower hallway 6 ft wide. What is the length of the longest pipe that can be carried horizontally around the corner? 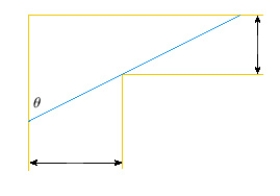


Unlock Deck
Unlock for access to all 153 flashcards in this deck.
Unlock Deck
k this deck
58
A fence 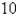 ft tall runs parallel to a tall building at a distance of
ft tall runs parallel to a tall building at a distance of 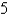 ft from the building. What is the length of the shortest ladder that will reach from the ground over the fence to the wall of the building? Round the result to the nearest hundredth.
ft from the building. What is the length of the shortest ladder that will reach from the ground over the fence to the wall of the building? Round the result to the nearest hundredth.
 ft tall runs parallel to a tall building at a distance of
ft tall runs parallel to a tall building at a distance of 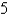 ft from the building. What is the length of the shortest ladder that will reach from the ground over the fence to the wall of the building? Round the result to the nearest hundredth.
ft from the building. What is the length of the shortest ladder that will reach from the ground over the fence to the wall of the building? Round the result to the nearest hundredth.
Unlock Deck
Unlock for access to all 153 flashcards in this deck.
Unlock Deck
k this deck
59
Find two numbers whose difference is 170 and whose product is a minimum.

Unlock Deck
Unlock for access to all 153 flashcards in this deck.
Unlock Deck
k this deck
60
If an open box is made from a metal sheet 9 in. square by cutting out identical squares from each corner an bending up the resulting flaps, determine the dimensions of the box with the largest volume that can be made.

Unlock Deck
Unlock for access to all 153 flashcards in this deck.
Unlock Deck
k this deck
61
Sketch the graph of the function 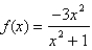 using the curve-sketching guidelines.
using the curve-sketching guidelines.
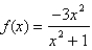 using the curve-sketching guidelines.
using the curve-sketching guidelines.
Unlock Deck
Unlock for access to all 153 flashcards in this deck.
Unlock Deck
k this deck
62
Sketch the curve. 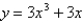
A)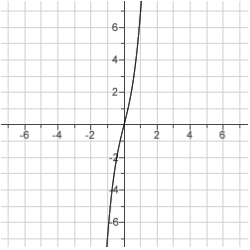
B)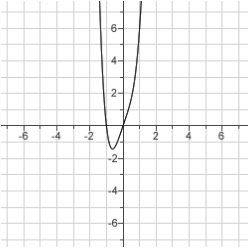
C)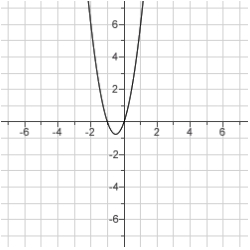
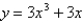
A)

B)

C)


Unlock Deck
Unlock for access to all 153 flashcards in this deck.
Unlock Deck
k this deck
63
Sketch the curve. Find the equation of the slant asymptote. 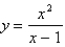
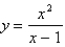

Unlock Deck
Unlock for access to all 153 flashcards in this deck.
Unlock Deck
k this deck
64
An efficiency study showed that the total number of cell phones assembled by the average worker at a manufacturing company t hours after starting work at 8 a.m.is given by 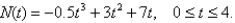
Sketch the graph of the function N, and interpret your result.
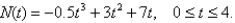
Sketch the graph of the function N, and interpret your result.

Unlock Deck
Unlock for access to all 153 flashcards in this deck.
Unlock Deck
k this deck
65
Sketch the graph of the function 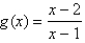 using the curve-sketching guidelines.
using the curve-sketching guidelines.
A)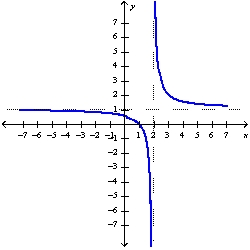
B)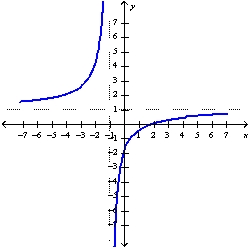
C)
D)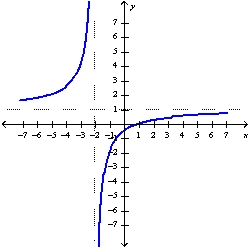
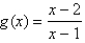 using the curve-sketching guidelines.
using the curve-sketching guidelines.A)

B)

C)

D)


Unlock Deck
Unlock for access to all 153 flashcards in this deck.
Unlock Deck
k this deck
66
Find the horizontal and vertical asymptotes of the graph of the function 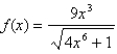 .
.
A)HA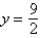 , VA
, VA 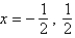
B)HA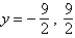 , VA none
, VA none
C)HA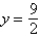 , VA none
, VA none
D)HA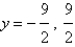 , VA
, VA 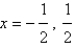
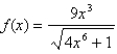 .
.A)HA
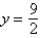 , VA
, VA 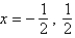
B)HA
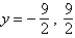 , VA none
, VA noneC)HA
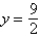 , VA none
, VA noneD)HA
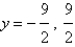 , VA
, VA 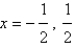

Unlock Deck
Unlock for access to all 153 flashcards in this deck.
Unlock Deck
k this deck
67
Find the slant asymptote of the graph of 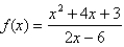 using the curve-sketching guidelines.
using the curve-sketching guidelines.
A)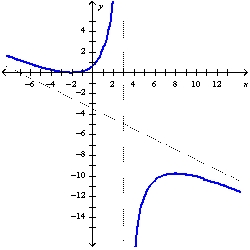
B)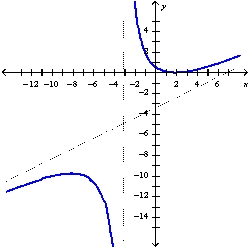
C)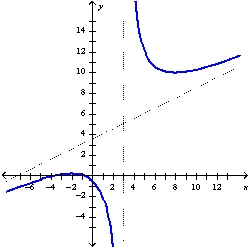
D)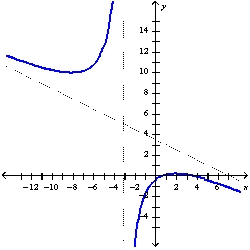
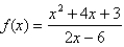 using the curve-sketching guidelines.
using the curve-sketching guidelines.A)

B)

C)

D)


Unlock Deck
Unlock for access to all 153 flashcards in this deck.
Unlock Deck
k this deck
68
A skydiver leaps from a helicopter hovering high above the ground. Her velocity t sec later and before deploying her parachute is given by 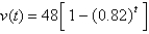 where
where 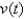 is measured in meters per second. What is her terminal velocity? Hint: Evaluate
is measured in meters per second. What is her terminal velocity? Hint: Evaluate 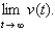
A)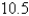 m/sec
m/sec
B)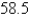 m/sec
m/sec
C)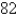 m/sec
m/sec
D)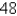 m/sec
m/sec
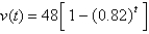 where
where 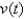 is measured in meters per second. What is her terminal velocity? Hint: Evaluate
is measured in meters per second. What is her terminal velocity? Hint: Evaluate 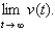
A)
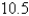 m/sec
m/secB)
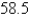 m/sec
m/secC)
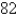 m/sec
m/secD)
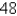 m/sec
m/sec
Unlock Deck
Unlock for access to all 153 flashcards in this deck.
Unlock Deck
k this deck
69
Find the limit. 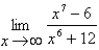
A)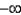
B)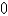
C)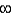
D)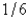
E)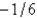
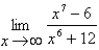
A)
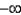
B)
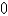
C)
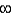
D)
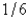
E)
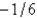

Unlock Deck
Unlock for access to all 153 flashcards in this deck.
Unlock Deck
k this deck
70
Find the limit. 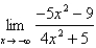
A)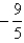
B)0
C)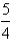
D)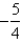
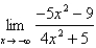
A)
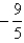
B)0
C)
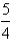
D)
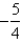

Unlock Deck
Unlock for access to all 153 flashcards in this deck.
Unlock Deck
k this deck
71
Sketch the curve. 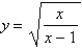
A)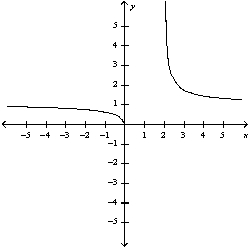
B)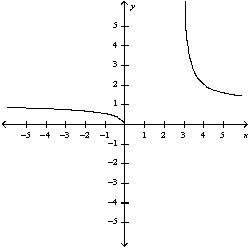
C)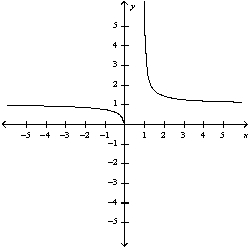
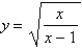
A)

B)

C)


Unlock Deck
Unlock for access to all 153 flashcards in this deck.
Unlock Deck
k this deck
72
Sketch the graph of the function 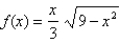 using the curve-sketching guidelines.
using the curve-sketching guidelines.
A)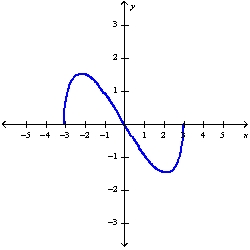
B)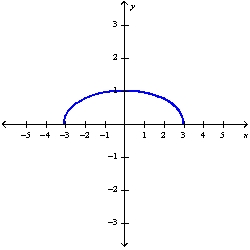
C)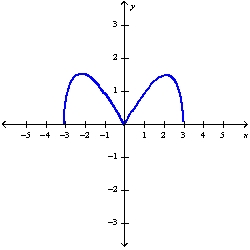
D)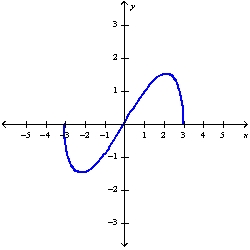
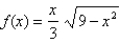 using the curve-sketching guidelines.
using the curve-sketching guidelines.A)

B)

C)

D)


Unlock Deck
Unlock for access to all 153 flashcards in this deck.
Unlock Deck
k this deck
73
Sketch the graph of the function  using the curve-sketching guidelines.
using the curve-sketching guidelines.
A)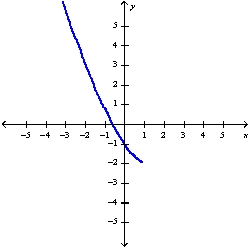
B)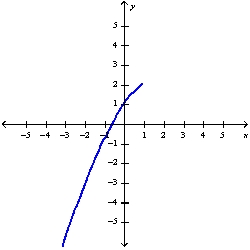
C)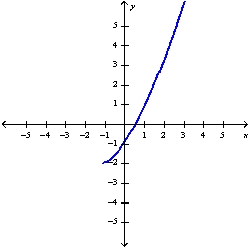
D)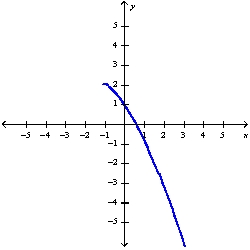
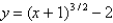 using the curve-sketching guidelines.
using the curve-sketching guidelines.A)

B)
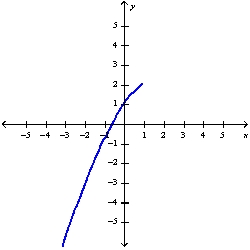
C)
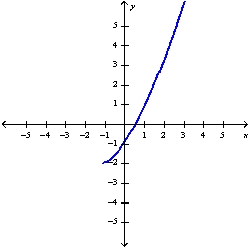
D)
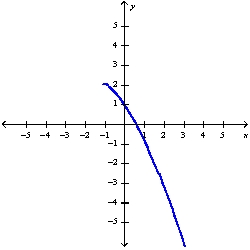

Unlock Deck
Unlock for access to all 153 flashcards in this deck.
Unlock Deck
k this deck
74
Sketch the graph of the function 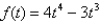 using the curve-sketching guidelines.
using the curve-sketching guidelines.
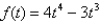 using the curve-sketching guidelines.
using the curve-sketching guidelines.
Unlock Deck
Unlock for access to all 153 flashcards in this deck.
Unlock Deck
k this deck
75
Sketch the graph of the function 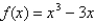 using the curve-sketching guidelines.
using the curve-sketching guidelines.
A)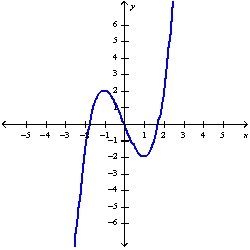
B)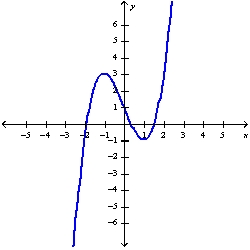
C)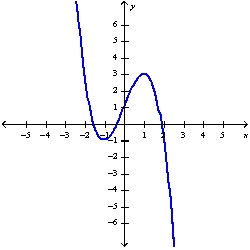
D)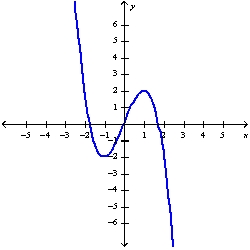
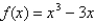 using the curve-sketching guidelines.
using the curve-sketching guidelines.A)

B)

C)

D)


Unlock Deck
Unlock for access to all 153 flashcards in this deck.
Unlock Deck
k this deck
76
Sketch the graph of the function 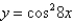 on
on 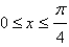 using the curve-sketching guidelines.
using the curve-sketching guidelines.
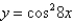 on
on 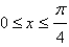 using the curve-sketching guidelines.
using the curve-sketching guidelines.
Unlock Deck
Unlock for access to all 153 flashcards in this deck.
Unlock Deck
k this deck
77
Sketch the graph of the function 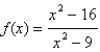 using the curve-sketching guidelines.
using the curve-sketching guidelines.
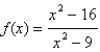 using the curve-sketching guidelines.
using the curve-sketching guidelines.
Unlock Deck
Unlock for access to all 153 flashcards in this deck.
Unlock Deck
k this deck
78
Sketch the curve. 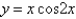 ,
, 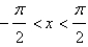
A)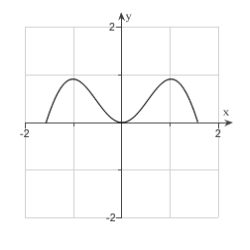
B)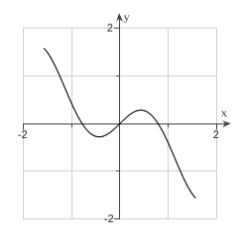
C)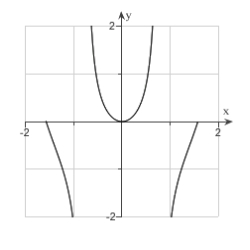
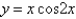 ,
, 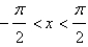
A)

B)

C)


Unlock Deck
Unlock for access to all 153 flashcards in this deck.
Unlock Deck
k this deck
79
Let 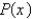 and
and 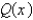 be polynomials. Find
be polynomials. Find 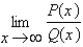 if the degree of
if the degree of 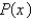 is
is 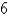 and the degree of
and the degree of 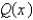 is
is 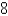 .
.
A)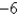
B)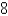
C)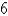
D)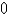
E)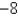
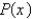 and
and 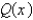 be polynomials. Find
be polynomials. Find 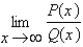 if the degree of
if the degree of 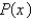 is
is 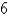 and the degree of
and the degree of 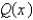 is
is 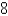 .
.A)
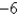
B)
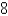
C)
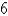
D)
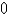
E)
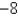

Unlock Deck
Unlock for access to all 153 flashcards in this deck.
Unlock Deck
k this deck
80
Find the slant asymptote of the function 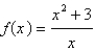 .
.
A)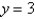
B)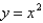
C)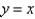
D)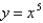
E)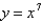
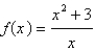 .
.A)
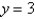
B)
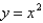
C)
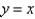
D)
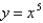
E)
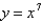

Unlock Deck
Unlock for access to all 153 flashcards in this deck.
Unlock Deck
k this deck


