Deck 16: Vector Calculus
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/137
Play
Full screen (f)
Deck 16: Vector Calculus
1
Use Stoke's theorem to evaluate 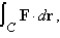
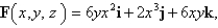 C is the curve of intersection of the hyperbolic paraboloid
C is the curve of intersection of the hyperbolic paraboloid 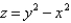 and the cylinder
and the cylinder 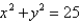 oriented counterclockwise as viewed from above.
oriented counterclockwise as viewed from above.
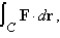
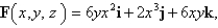 C is the curve of intersection of the hyperbolic paraboloid
C is the curve of intersection of the hyperbolic paraboloid 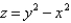 and the cylinder
and the cylinder 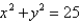 oriented counterclockwise as viewed from above.
oriented counterclockwise as viewed from above.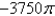
2
Find parametric equations for C, if C is the curve of intersection of the hyperbolic paraboloid 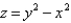 and the cylinder
and the cylinder 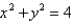 oriented counterclockwise as viewed from above.
oriented counterclockwise as viewed from above.
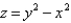 and the cylinder
and the cylinder 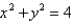 oriented counterclockwise as viewed from above.
oriented counterclockwise as viewed from above.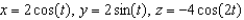
3
Use Stoke's theorem to evaluate 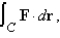 where
where 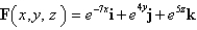 and C is the boundary of the part of the plane
and C is the boundary of the part of the plane 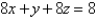 in the first octant.
in the first octant.
A)16
B)0
C)49
D)69
E)23
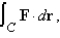 where
where 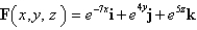 and C is the boundary of the part of the plane
and C is the boundary of the part of the plane 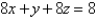 in the first octant.
in the first octant.A)16
B)0
C)49
D)69
E)23
0
4
Suppose that 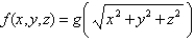 where g is a function of one variable such that
where g is a function of one variable such that 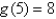 . Evaluate
. Evaluate 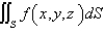 where S is the sphere
where S is the sphere 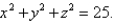
A)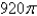
B)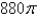
C)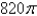
D)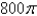
E)None of these
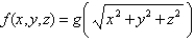 where g is a function of one variable such that
where g is a function of one variable such that 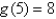 . Evaluate
. Evaluate 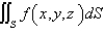 where S is the sphere
where S is the sphere 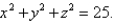
A)
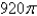
B)
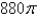
C)
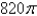
D)
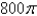
E)None of these

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
5
Use Stokes' Theorem to evaluate 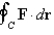 .
. 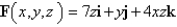 ;
;
C is the boundary of the triangle with vertices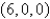 ,
, 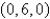 , and
, and 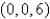 oriented in a counterclockwise direction when viewed from above
oriented in a counterclockwise direction when viewed from above
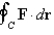 .
. 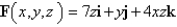 ;
;C is the boundary of the triangle with vertices
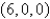 ,
, 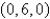 , and
, and 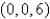 oriented in a counterclockwise direction when viewed from above
oriented in a counterclockwise direction when viewed from above
Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
6
Assuming that S satisfies the conditions of the Divergence Theorem and the scalar functions and components of the vector fields have continuous second order partial derivatives, find 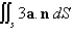 , where a is the constant vector.
, where a is the constant vector.
A)5
B)3
C)8
D)7
E)6
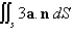 , where a is the constant vector.
, where a is the constant vector.A)5
B)3
C)8
D)7
E)6

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
7
Use a computer algebra system to compute the flux of F across S. S is the surface of the cube cut from the first octant by the planes 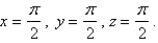
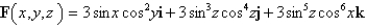
A)3
B)4
C)1
D)0.67
E)
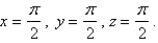
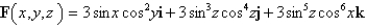
A)3
B)4
C)1
D)0.67
E)
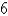

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
8
Evaluate the surface integral. Round your answer to four decimal places. 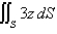 S is surface
S is surface 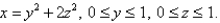
A)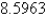
B)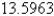
C)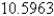
D)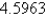
E)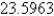
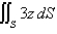 S is surface
S is surface 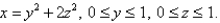
A)
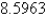
B)
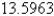
C)
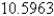
D)
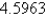
E)
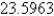

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
9
Use Stoke's theorem to calculate the surface integral 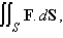 where
where 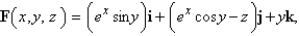 and S is the part of the cone
and S is the part of the cone 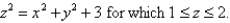
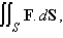 where
where 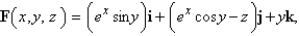 and S is the part of the cone
and S is the part of the cone 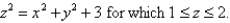

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
10
Use Stokes' Theorem to evaluate 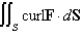 .
. 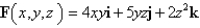 ;
;
S is the part of the ellipsoid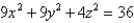 lying above the xy-plane and oriented with normal pointing upward.
lying above the xy-plane and oriented with normal pointing upward.
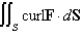 .
. 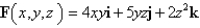 ;
;S is the part of the ellipsoid
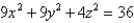 lying above the xy-plane and oriented with normal pointing upward.
lying above the xy-plane and oriented with normal pointing upward.
Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
11
The temperature at the point 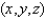 in a substance with conductivity
in a substance with conductivity 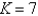 is
is 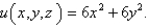 Find the rate of heat flow inward across the cylindrical
Find the rate of heat flow inward across the cylindrical 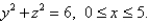
A)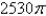
B)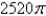
C)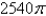
D)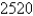
E)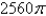
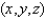 in a substance with conductivity
in a substance with conductivity 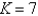 is
is 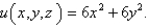 Find the rate of heat flow inward across the cylindrical
Find the rate of heat flow inward across the cylindrical 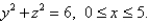
A)
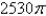
B)
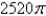
C)
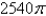
D)
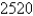
E)
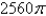

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
12
Use Stokes' Theorem to evaluate 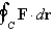 .
. 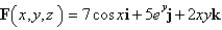 ; C is the curve obtained by intersecting the cylinder
; C is the curve obtained by intersecting the cylinder 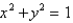 with the hyperbolic paraboloid
with the hyperbolic paraboloid 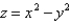 , oriented in a counterclockwise direction when viewed from above
, oriented in a counterclockwise direction when viewed from above
A)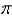
B)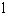
C)0
D)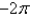
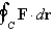 .
. 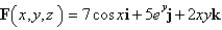 ; C is the curve obtained by intersecting the cylinder
; C is the curve obtained by intersecting the cylinder 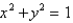 with the hyperbolic paraboloid
with the hyperbolic paraboloid 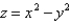 , oriented in a counterclockwise direction when viewed from above
, oriented in a counterclockwise direction when viewed from aboveA)
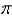
B)
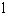
C)0
D)
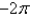

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
13
Use Stoke's theorem to evaluate 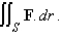
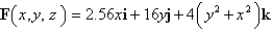 C is the boundary of the part of the paraboloid
C is the boundary of the part of the paraboloid 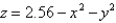 in the first octant. C is oriented counterclockwise as viewed from above.
in the first octant. C is oriented counterclockwise as viewed from above.
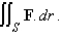
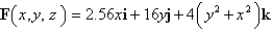 C is the boundary of the part of the paraboloid
C is the boundary of the part of the paraboloid 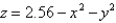 in the first octant. C is oriented counterclockwise as viewed from above.
in the first octant. C is oriented counterclockwise as viewed from above.
Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
14
Use the Divergence Theorem to calculate the surface integral 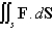 ; that is, calculate the flux of
; that is, calculate the flux of 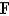 across
across 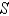 .
. 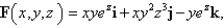 S is the surface of the box bounded by the coordinate planes and the planes
S is the surface of the box bounded by the coordinate planes and the planes 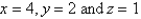 .
.
A)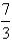
B)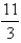
C)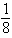
D)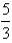
E)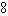
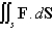 ; that is, calculate the flux of
; that is, calculate the flux of 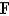 across
across 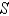 .
. 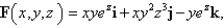 S is the surface of the box bounded by the coordinate planes and the planes
S is the surface of the box bounded by the coordinate planes and the planes 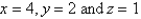 .
.A)
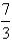
B)
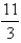
C)
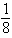
D)
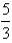
E)
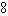

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
15
Evaluate 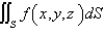 .
. 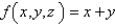 ; S is the part of the plane
; S is the part of the plane 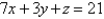 in the first octant.
in the first octant.
A)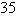
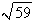
B)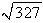
C)0
D)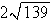
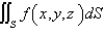 .
. 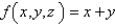 ; S is the part of the plane
; S is the part of the plane 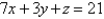 in the first octant.
in the first octant.A)
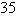
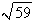
B)
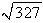
C)0
D)
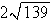

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
16
Use Stokes' Theorem to evaluate 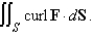 S consists of the top and the four sides (but not the bottom) of the cube with vertices
S consists of the top and the four sides (but not the bottom) of the cube with vertices 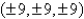 oriented outward.
oriented outward. 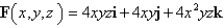
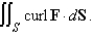 S consists of the top and the four sides (but not the bottom) of the cube with vertices
S consists of the top and the four sides (but not the bottom) of the cube with vertices 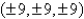 oriented outward.
oriented outward. 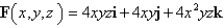

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
17
Use Stoke's theorem to evaluate 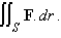
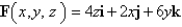 C is the curve of intersection of the plane z = x + 9 and the cylinder
C is the curve of intersection of the plane z = x + 9 and the cylinder 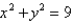
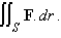
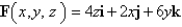 C is the curve of intersection of the plane z = x + 9 and the cylinder
C is the curve of intersection of the plane z = x + 9 and the cylinder 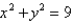

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
18
Use Stokes' Theorem to evaluate 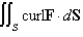 .
. 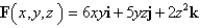 ; S is the part of the paraboloid
; S is the part of the paraboloid 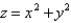 lying below the plane
lying below the plane 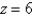 and oriented with normal pointing downward.
and oriented with normal pointing downward.
A)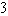
B)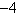
C)0
D)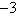
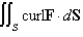 .
. 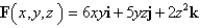 ; S is the part of the paraboloid
; S is the part of the paraboloid 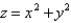 lying below the plane
lying below the plane 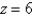 and oriented with normal pointing downward.
and oriented with normal pointing downward.A)
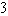
B)
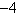
C)0
D)
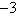

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
19
Evaluate the surface integral. 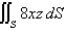 S is the part of the plane
S is the part of the plane 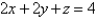 that lies in the first octant.
that lies in the first octant.
A)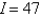
B)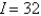
C)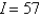
D)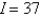
E)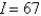
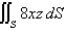 S is the part of the plane
S is the part of the plane 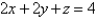 that lies in the first octant.
that lies in the first octant.A)
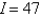
B)
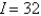
C)
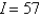
D)
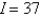
E)
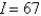

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
20
Use Stokes' Theorem to evaluate 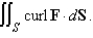
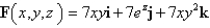 S consists of the four sides of the pyramid with vertices (0, 0, 0), (3, 0, 0), (0, 0, 3), (3, 0,3) and (0, 3, 0) that lie to the right of the xz-plane, oriented in the direction of the positive y-axis.
S consists of the four sides of the pyramid with vertices (0, 0, 0), (3, 0, 0), (0, 0, 3), (3, 0,3) and (0, 3, 0) that lie to the right of the xz-plane, oriented in the direction of the positive y-axis.
A)1
B)16
C)49
D)0
E)12
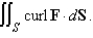
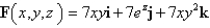 S consists of the four sides of the pyramid with vertices (0, 0, 0), (3, 0, 0), (0, 0, 3), (3, 0,3) and (0, 3, 0) that lie to the right of the xz-plane, oriented in the direction of the positive y-axis.
S consists of the four sides of the pyramid with vertices (0, 0, 0), (3, 0, 0), (0, 0, 3), (3, 0,3) and (0, 3, 0) that lie to the right of the xz-plane, oriented in the direction of the positive y-axis.A)1
B)16
C)49
D)0
E)12

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
21
Find the area of the surface. The part of the plane 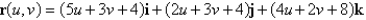 ;
; 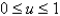 ,
, 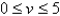
A)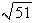
B)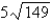
C)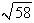
D)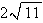
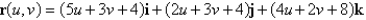 ;
; 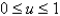 ,
, 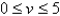
A)
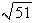
B)
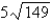
C)
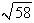
D)
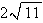

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
22
Find the area of the part of the cone 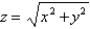 that is cut off by the cylinder
that is cut off by the cylinder 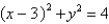
A)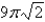
B)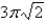
C)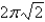
D)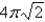
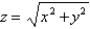 that is cut off by the cylinder
that is cut off by the cylinder 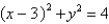
A)
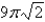
B)
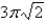
C)
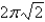
D)
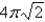

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
23
Find the mass of the surface S having the given mass density. S is the hemisphere 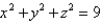 ,
, 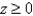 ; the density at a point P on S is equal to the distance between P and the xy-plane.
; the density at a point P on S is equal to the distance between P and the xy-plane.
A)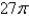
B)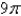
C)9
D)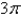
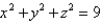 ,
, 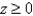 ; the density at a point P on S is equal to the distance between P and the xy-plane.
; the density at a point P on S is equal to the distance between P and the xy-plane.A)
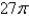
B)
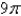
C)9
D)
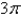

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
24
A fluid with density  flows with velocity
flows with velocity 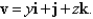 Find the rate of flow upward through the paraboloid
Find the rate of flow upward through the paraboloid 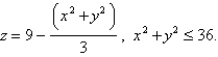
 flows with velocity
flows with velocity 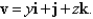 Find the rate of flow upward through the paraboloid
Find the rate of flow upward through the paraboloid 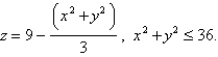

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
25
Find the moment of inertia about the z-axis of a thin funnel in the shape of a cone 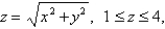 if its density function is
if its density function is 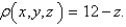
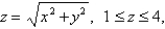 if its density function is
if its density function is 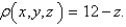

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
26
Evaluate 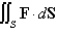 , that is, find the flux of F across S.
, that is, find the flux of F across S. 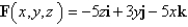 ; S is the hemisphere
; S is the hemisphere 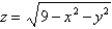 ; n points upward.
; n points upward.
A)162
B)162
C)
D)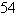
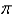
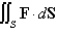 , that is, find the flux of F across S.
, that is, find the flux of F across S. 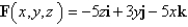 ; S is the hemisphere
; S is the hemisphere 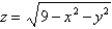 ; n points upward.
; n points upward.A)162
B)162
C)
D)
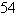
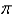

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
27
Evaluate 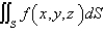 .
. 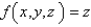 ; S is the part of the torus with vector representation
; S is the part of the torus with vector representation 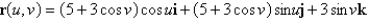 ,
, 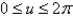 ,
, 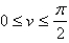 .
.
A)
B)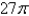
C)0
D)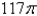
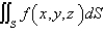 .
. 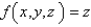 ; S is the part of the torus with vector representation
; S is the part of the torus with vector representation 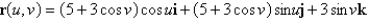 ,
, 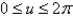 ,
, 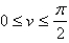 .
.A)
B)
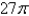
C)0
D)

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
28
Find a parametric representation for the part of the elliptic paraboloid 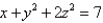 that lies in front of the plane x = 0.
that lies in front of the plane x = 0.
A)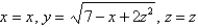
B)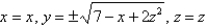
C)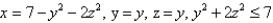
D)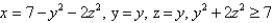
E)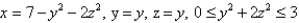
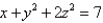 that lies in front of the plane x = 0.
that lies in front of the plane x = 0.A)
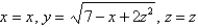
B)
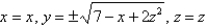
C)
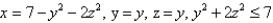
D)
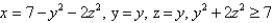
E)
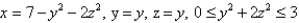

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
29
Evaluate the surface integral. S is the part of the cylinder 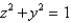 between the planes
between the planes 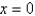 and
and 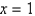 in the first octant.
in the first octant. 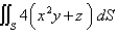
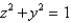 between the planes
between the planes 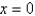 and
and 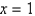 in the first octant.
in the first octant. 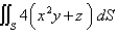

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
30
Use Gauss's Law to find the charge contained in the solid hemisphere 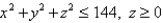 , if the electric field is
, if the electric field is 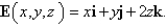
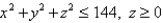 , if the electric field is
, if the electric field is 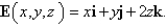

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
31
Match the equation with one of the graphs below. 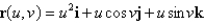
A)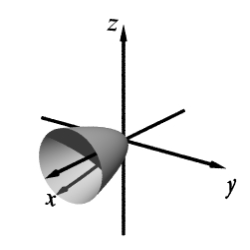
B)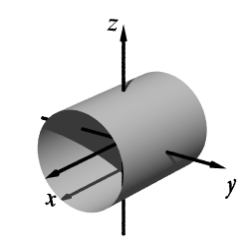
C)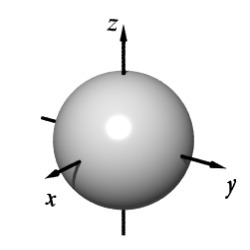
D)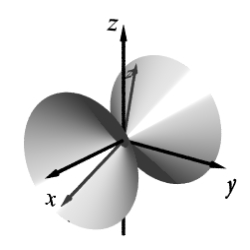
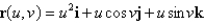
A)

B)

C)

D)


Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
32
Evaluate 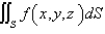 .
. 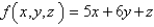 ; S is the part of the cone
; S is the part of the cone 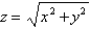 between the planes
between the planes 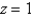 and
and 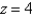 .
.
A)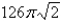
B)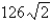
C)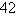
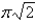
D)0
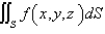 .
. 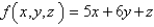 ; S is the part of the cone
; S is the part of the cone 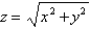 between the planes
between the planes 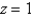 and
and 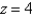 .
.A)
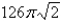
B)
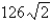
C)
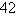
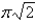
D)0

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
33
Evaluate 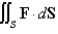 , that is, find the flux of F across S.
, that is, find the flux of F across S. 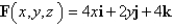 ; S is the part of the paraboloid
; S is the part of the paraboloid 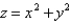 between the planes z = 0 and z = 5; n points upward.
between the planes z = 0 and z = 5; n points upward.
 , that is, find the flux of F across S.
, that is, find the flux of F across S. 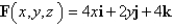 ; S is the part of the paraboloid
; S is the part of the paraboloid 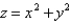 between the planes z = 0 and z = 5; n points upward.
between the planes z = 0 and z = 5; n points upward.
Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
34
Evaluate the surface integral 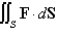 for the given vector field F and the oriented surface S. In other words, find the flux of F across S.
for the given vector field F and the oriented surface S. In other words, find the flux of F across S. 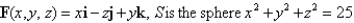 in the first octant,
in the first octant,
with orientation toward the origin.
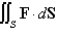 for the given vector field F and the oriented surface S. In other words, find the flux of F across S.
for the given vector field F and the oriented surface S. In other words, find the flux of F across S. 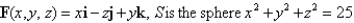 in the first octant,
in the first octant,with orientation toward the origin.

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
35
Let S be the cube with vertices 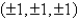 . Approximate
. Approximate 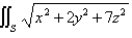 by using a Riemann sum as in Definition 1, taking the patches
by using a Riemann sum as in Definition 1, taking the patches 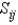 to be the squares that are the faces of the cube and the points
to be the squares that are the faces of the cube and the points 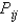 to be the centers of the squares.
to be the centers of the squares.
A)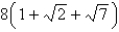
B)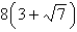
C)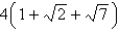
D)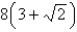
E)none of these
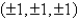 . Approximate
. Approximate 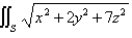 by using a Riemann sum as in Definition 1, taking the patches
by using a Riemann sum as in Definition 1, taking the patches 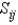 to be the squares that are the faces of the cube and the points
to be the squares that are the faces of the cube and the points 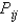 to be the centers of the squares.
to be the centers of the squares.A)
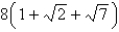
B)
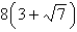
C)
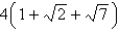
D)
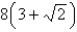
E)none of these

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
36
Find the area of the surface. The part of the paraboloid 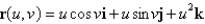 ;
; 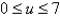 ,
, 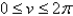
A)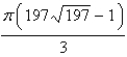
B)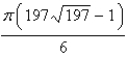
C)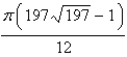
D)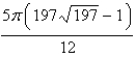
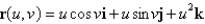 ;
; 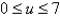 ,
, 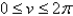
A)
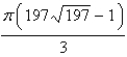
B)
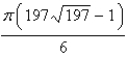
C)
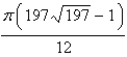
D)
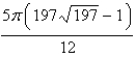

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
37
Find the mass of the surface S having the given mass density. S is part of the plane 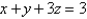 in the first octant; the density at a point P on S is equal to the square of the distance between P and the xy-plane.
in the first octant; the density at a point P on S is equal to the square of the distance between P and the xy-plane.
A)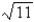
B)49
C)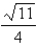
D)20
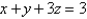 in the first octant; the density at a point P on S is equal to the square of the distance between P and the xy-plane.
in the first octant; the density at a point P on S is equal to the square of the distance between P and the xy-plane.A)
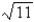
B)49
C)
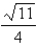
D)20

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
38
Find the area of the surface. The part of the paraboloid 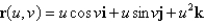 ;
; 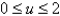 ,
, 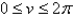
A)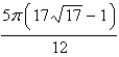
B)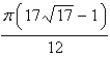
C)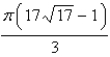
D)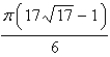
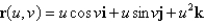 ;
; 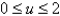 ,
, 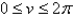
A)
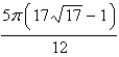
B)
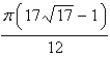
C)
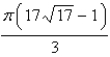
D)
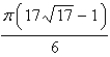

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
39
Evaluate the surface integral 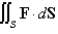 for the given vector field F and the oriented surface S. In other words, find the flux of F across S.
for the given vector field F and the oriented surface S. In other words, find the flux of F across S. 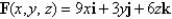

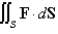 for the given vector field F and the oriented surface S. In other words, find the flux of F across S.
for the given vector field F and the oriented surface S. In other words, find the flux of F across S. 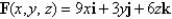


Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
40
Evaluate the surface integral where S is the surface with parametric equations 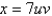 ,
, 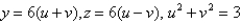 .
. 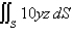
A)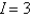
B)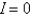
C)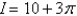
D)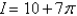
E)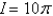
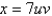 ,
, 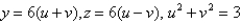 .
. 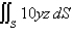
A)
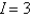
B)
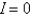
C)
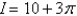
D)
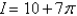
E)
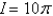

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
41
Find the area of the part of paraboloid 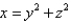 that lies inside the cylinder
that lies inside the cylinder 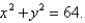
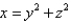 that lies inside the cylinder
that lies inside the cylinder 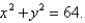

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
42
Below is given the plot of a vector field F in the xy-plane. (The z-component of F is 0.) By studying the plot, determine whether div F is positive, negative, or zero. 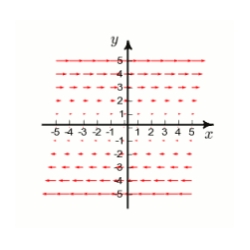
A)cannot be determined
B)positive
C)negative
D)zero

A)cannot be determined
B)positive
C)negative
D)zero

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
43
Find the area of the surface S where S is the part of the plane 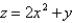 that lies above the triangular region with vertices
that lies above the triangular region with vertices 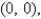
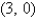 , and
, and 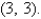
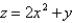 that lies above the triangular region with vertices
that lies above the triangular region with vertices 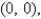
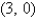 , and
, and 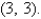

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
44
Use the Divergence Theorem to find the flux of F across S; that is, calculate 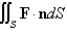 .
. 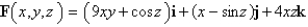 ; S is the sphere
; S is the sphere 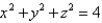
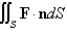 .
. 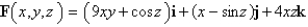 ; S is the sphere
; S is the sphere 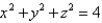

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
45
Find the area of the surface S where S is the part of the sphere 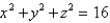 that lies to the right of the xz-plane and inside the cylinder
that lies to the right of the xz-plane and inside the cylinder 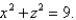
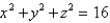 that lies to the right of the xz-plane and inside the cylinder
that lies to the right of the xz-plane and inside the cylinder 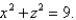

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
46
Let 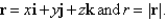
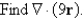
A)27
B)18
C)45
D)9
E)None of these
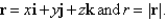
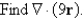
A)27
B)18
C)45
D)9
E)None of these

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
47
Find an equation in rectangular coordinates, and then identify the surface. 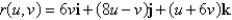
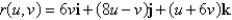

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
48
Find the correct identity, if f is a scalar field, F and G are vector fields.
A)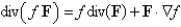
B)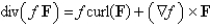
C)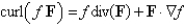
D)None of these
A)
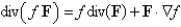
B)
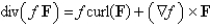
C)
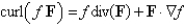
D)None of these

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
49
Set up, but do not evaluate, a double integral for the area of the surface with parametric equations 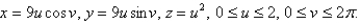
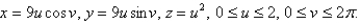

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
50
Find the area of the part of the surface 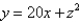 that lies between the planes x = 0, x = 4,
that lies between the planes x = 0, x = 4, 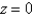 , and z = 1.
, and z = 1.
A)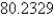
B)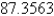
C)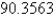
D)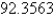
E)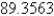
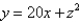 that lies between the planes x = 0, x = 4,
that lies between the planes x = 0, x = 4, 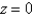 , and z = 1.
, and z = 1.A)
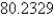
B)
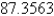
C)
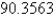
D)
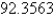
E)
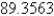

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
51
Find an equation of the tangent plane to the parametric surface represented by r at the specified point. 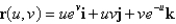 ; u = ln 5, v = 0
; u = ln 5, v = 0
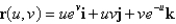 ; u = ln 5, v = 0
; u = ln 5, v = 0
Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
52
Find a parametric representation for the part of the sphere 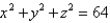 that lies above the cone
that lies above the cone 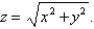
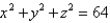 that lies above the cone
that lies above the cone 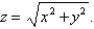

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
53
Find the divergence of the vector field F. 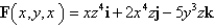
A)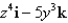
B)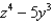
C)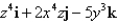
D)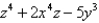
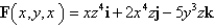
A)
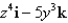
B)
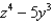
C)
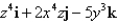
D)
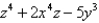

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
54
Find the area of the surface S where S is the part of the surface 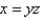 that lies inside the cylinder
that lies inside the cylinder 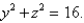
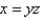 that lies inside the cylinder
that lies inside the cylinder 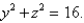

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
55
Find an equation of the tangent plane to the parametric surface represented by r at the specified point. 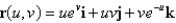 ; u = ln 9, v = 0
; u = ln 9, v = 0
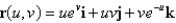 ; u = ln 9, v = 0
; u = ln 9, v = 0
Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
56
Find an equation of the tangent plane to the parametric surface represented by r at the specified point. 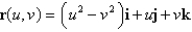 ;
; 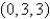
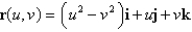 ;
; 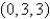

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
57
Find a vector representation for the surface.
The plane that passes through the point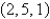 and contains the vectors
and contains the vectors 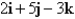 and
and 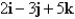 ..
..
The plane that passes through the point
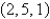 and contains the vectors
and contains the vectors 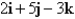 and
and 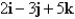 ..
..
Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
58
Find a parametric representation for the part of the plane 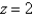 that lies inside the cylinder
that lies inside the cylinder 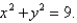
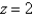 that lies inside the cylinder
that lies inside the cylinder 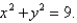

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
59
Find the area of the surface S where S is the part of the sphere 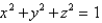 that lies inside the cylinder
that lies inside the cylinder 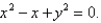
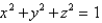 that lies inside the cylinder
that lies inside the cylinder 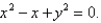

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
60
Find an equation in rectangular coordinates, and then identify the surface. 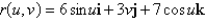
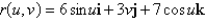

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
61
Determine whether or not vector field is conservative. If it is conservative, find a function f such that 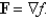
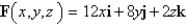
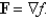
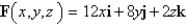

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
62
Find the curl of the vector field F. 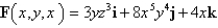
A)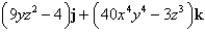
B)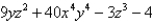
C)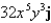
D)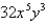
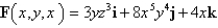
A)
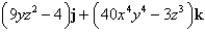
B)
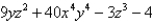
C)
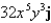
D)
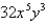

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
63
Let 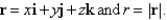
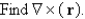
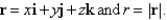
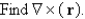

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
64
Find the curl of the vector field. 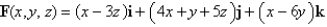
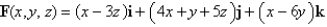

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
65
Find the curl of 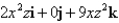 .
.
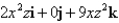 .
.
Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
66
Use Green's Theorem and/or a computer algebra system to evaluate 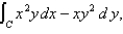 where C is the circle
where C is the circle 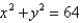 with counterclockwise orientation.
with counterclockwise orientation.
A)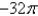
B)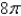
C)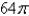
D)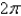
E)None of these
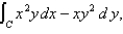 where C is the circle
where C is the circle 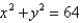 with counterclockwise orientation.
with counterclockwise orientation.A)
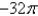
B)
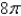
C)
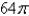
D)
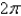
E)None of these

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
67
Find the divergence of the vector field. 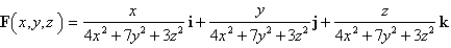
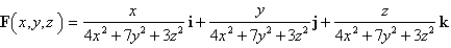

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
68
Find the div F if 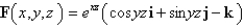 .
.
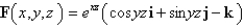 .
.
Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
69
Use Green's Theorem to evaluate the line integral along the positively oriented closed curve C. 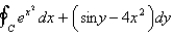 , where C is the boundary of the region bounded by the parabolas
, where C is the boundary of the region bounded by the parabolas 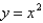 and
and 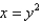 .
.
A)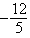
B)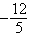 + e
+ e
C)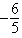 + e
+ e
D)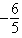
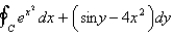 , where C is the boundary of the region bounded by the parabolas
, where C is the boundary of the region bounded by the parabolas 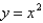 and
and 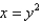 .
.A)
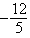
B)
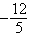 + e
+ eC)
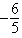 + e
+ eD)
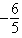

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
70
Let 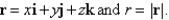
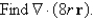
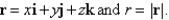
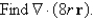

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
71
Find (a) the divergence and (b) the curl of the vector field F. 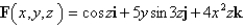
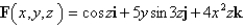

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
72
Let f be a scalar field. Determine whether the expression is meaningful. If so, state whether the expression represents a scalar field or a vector field. 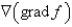
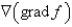

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
73
Let F be a vector field. Determine whether the expression is meaningful. If so, state whether the expression represents a scalar field or a vector field.
curl (div F)
curl (div F)

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
74
Let f be a scalar field. Determine whether the expression is meaningful. If so, state whether the expression represents a scalar field or a vector field.
curl f
curl f

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
75
Determine whether or not vector field is conservative. If it is conservative, find a function f such that 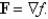
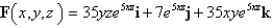
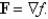
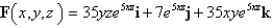

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
76
Find the curl of the vector field. 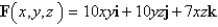
A)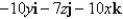
B)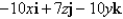
C)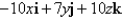
D)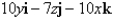
E)None of these
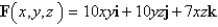
A)
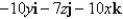
B)
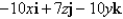
C)
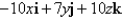
D)
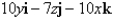
E)None of these

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
77
Use Green's Theorem to evaluate the line integral along the positively oriented closed curve C. 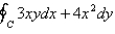 , where C is the triangle with vertices
, where C is the triangle with vertices 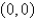 ,
, 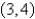 , and
, and 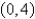 .
.
A)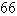
B)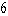
C)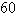
D)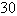
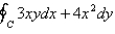 , where C is the triangle with vertices
, where C is the triangle with vertices 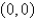 ,
, 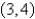 , and
, and 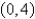 .
.A)
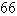
B)
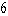
C)
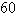
D)
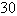

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
78
Let F be a vector field. Determine whether the expression is meaningful. If so, state whether the expression represents a scalar field or a vector field. 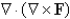
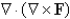

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
79
Find the curl of the vector field. 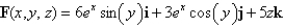
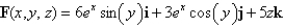

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
80
Let D be a region bounded by a simple closed path C in the xy. Then the coordinates of the centroid 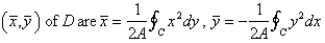 where A is the area of D. Find the centroid of the triangle with vertices (0, 0), (
where A is the area of D. Find the centroid of the triangle with vertices (0, 0), ( 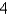 , 0) and (0,
, 0) and (0, 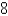 ).
).
A)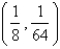
B)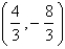
C)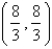
D)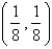
E)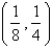
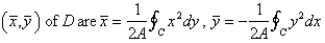 where A is the area of D. Find the centroid of the triangle with vertices (0, 0), (
where A is the area of D. Find the centroid of the triangle with vertices (0, 0), ( 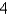 , 0) and (0,
, 0) and (0, 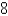 ).
).A)
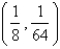
B)
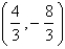
C)
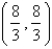
D)
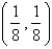
E)
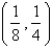

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck


