Deck 10: Parametric Equations and Polar Coordinates
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/73
Play
Full screen (f)
Deck 10: Parametric Equations and Polar Coordinates
1
In the LORAN (LOng RAnge Navigation) radio navigation system, two radio stations located at A and B transmit simultaneous signals to a ship or an aircraft located at P. The onboard computer converts the time difference in receiving these signals into a distance difference , and this, according to the definition of a hyperbola, locates the ship or aircraft on one branch of a hyperbola (see the figure). Suppose that station B is located L = mi due east of station A on a coastline. A ship received the signal from B microseconds (µs) before it received the signal from A. Assuming that radio signals travel at a speed of ft /µs and if the ship is due north of B, how far off the coastline is the ship? Round your answer to the nearest mile. 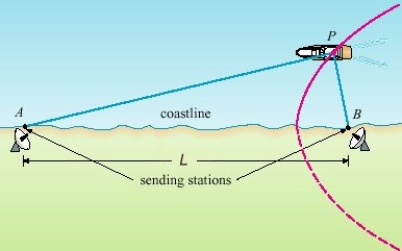
A) miles
B) miles
C) miles
D) miles
E) miles

A) miles
B) miles
C) miles
D) miles
E) miles
miles
2
The planet Mercury travels in an elliptical orbit with eccentricity . Its minimum distance from the Sun is km. If the perihelion distance from a planet to the Sun is and the aphelion distance is , find the maximum distance (in km) from Mercury to the Sun.
A) km
B) km
C) km
D) km
E) km
A) km
B) km
C) km
D) km
E) km
km
3
Find an equation of the hyperbola centered at the origin that satisfies the given condition. Vertices: (± 4, 0), asymptotes: y = ± x
A)
B)
C)
D)
A)
B)
C)
D)
4
Suppose a planet is discovered that revolves around its sun in an elliptical orbit with the sun at one focus. Its perihelion distance (minimum distance from the planet to the sun) is approximately 1.3 km, and its aphelion distance (maximum distance from the planet to the sun) is approximately 6.9 km. Approximate the eccentricity of the planet's orbit. Round to three decimal places.
A) 0.683
B) 5.308
C) 1.464
D) 0.188
A) 0.683
B) 5.308
C) 1.464
D) 0.188

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
5
Find the equation of the directrix of the conic.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
6
Find an equation of the hyperbola with vertices and asymptotes .
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
7
Consider the polar equation 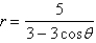 .
.
(a) Find the eccentricity and an equation of the directrix of the conic.
(b) Identify the conic.
(c) Sketch the curve.
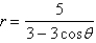 .
.(a) Find the eccentricity and an equation of the directrix of the conic.
(b) Identify the conic.
(c) Sketch the curve.

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
8
Find the eccentricity of the conic.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
9
Find an equation for the conic that satisfies the given conditions. hyperbola, foci (0, ± ) , vertices (0, ± )
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
10
Write a polar equation in r and of an ellipse with the focus at the origin, with the eccentricity and vertex at .
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
11
Write a polar equation in r and of a hyperbola with the focus at the origin, with the eccentricity and directrix .
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
12
Write a polar equation in r and of an ellipse with the focus at the origin, with the eccentricity and directrix .
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
13
Find an equation for the conic that satisfies the given conditions. parabola, vertex (0, 0), focus (0, - )
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
14
Write a polar equation of the conic that has a focus at the origin, eccentricity , and directrix . Identify the conic.
A) , hyperbola
B) , hyperbola
C) , ellipse
D) , ellipse
A) , hyperbola
B) , hyperbola
C) , ellipse
D) , ellipse

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
15
Match the equation with the correct graph.
A)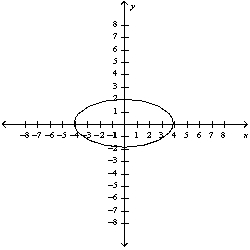
B)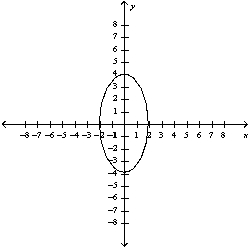
C)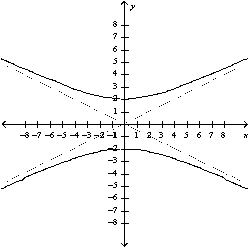
D)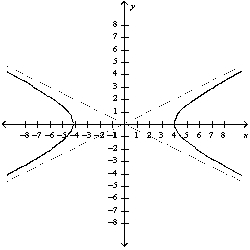
A)

B)

C)

D)


Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
16
Consider the polar equation 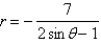 .
.
(a) Find the eccentricity and an equation of the directrix of the conic.
(b) Identify the conic.
(c) Sketch the curve.
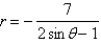 .
.(a) Find the eccentricity and an equation of the directrix of the conic.
(b) Identify the conic.
(c) Sketch the curve.

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
17
Find an equation of the parabola with focus and directrix .
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
18
Find an equation for the conic that satisfies the given conditions. ellipse, foci , length of major axis 8
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
19
The orbit of Hale-Bopp comet, discovered in 1995, is an ellipse with eccentricity and one focus at the Sun. The length of its major axis is AU. [An astronomical unit (AU) is the mean distance between Earth and the Sun, about 93 million miles.] Find the maximum distance from the comet to the Sun. (The perihelion distance from a planet to the Sun is and the aphelion distance is .) Find the answer in AU and round to the nearest hundredth.
A) AU
B) AU
C) AU
D) AU
E) AU
A) AU
B) AU
C) AU
D) AU
E) AU

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
20
Consider the polar equation 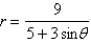 .
.
(a) Find the eccentricity and an equation of the directrix of the conic.
(b) Identify the conic.
(c) Sketch the curve.
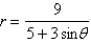 .
.(a) Find the eccentricity and an equation of the directrix of the conic.
(b) Identify the conic.
(c) Sketch the curve.

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
21
Find an equation of the conic satisfying the given conditions.
Hyperbola, foci (5, 6) and (5, -4), asymptotes x = 2y +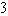 and x = - 2y +
and x = - 2y + 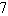
Hyperbola, foci (5, 6) and (5, -4), asymptotes x = 2y +
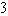 and x = - 2y +
and x = - 2y + 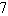

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
22
Find the area of the region that lies inside both curves. 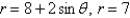
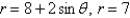

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
23
Find the area of the region that is bounded by the given curve and lies in the specified sector. 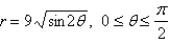
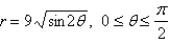

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
24
Find the area enclosed by the curve 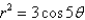 .
.
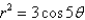 .
.
Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
25
Find the surface area generated by rotating the lemniscate about the line .
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
26
The graph of the following curve is given. Find the area that it encloses. 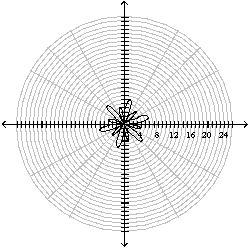
A)
B)
C)
D)
E) A =

A)
B)
C)
D)
E) A =

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
27
Find the length of the polar curve.
A)
B)
C)
D)
E) None of these
A)
B)
C)
D)
E) None of these

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
28
Find the area of the region enclosed by one loop of the curve.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
29
Using the arc length formula, set up, but do not evaluate, an integral equal to the total arc length of the ellipse. 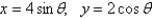
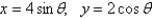

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
30
Find an equation of the ellipse that satisfies the given conditions. Foci: (0, ± 1), vertices (0, ± 6)
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
31
Graph of the following curve is given. Find its length. 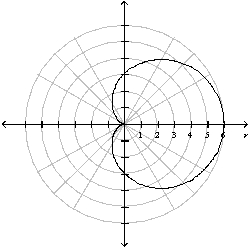
A) L = 25
B) L = 24
C) L = 26
D) L = 32
E) L = 20

A) L = 25
B) L = 24
C) L = 26
D) L = 32
E) L = 20

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
32
Find the vertex, focus, and directrix fo the parabola. 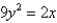
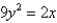

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
33
Find an equation of the ellipse that satisfies the given conditions. Foci: (0, ± 8), vertices (0, ± 9)
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
34
Find the area of the region that lies inside the first curve and outside the second curve.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
35
Use a graph to estimate the values of for which the curves and intersect. Round your answer to two decimal places.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
36
Find the vertices, foci, and asymptotes of the hyperbola. 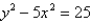
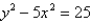

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
37
Find the vertex, focus, and directrix of the parabola. 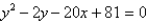
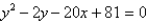

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
38
Find an equation of the conic satisfying the given conditions.
Hyperbola, foci (5, 6) and (5, -2), asymptotes x = 2y +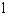 and x = - 2y +
and x = - 2y + 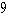
Hyperbola, foci (5, 6) and (5, -2), asymptotes x = 2y +
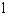 and x = - 2y +
and x = - 2y + 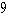

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
39
The point in a lunar orbit nearest the surface of the moon is called perilune and the point farthest from the surface is called apolune. The Apollo 11 spacecraft was placed in an elliptical lunar orbit with perilune altitude 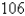 km and apolune altitude
km and apolune altitude 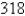 km (above the moon). Find an equation of this ellipse if the radius of the moon is
km (above the moon). Find an equation of this ellipse if the radius of the moon is 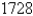 km and the center of the moon is at one focus.
km and the center of the moon is at one focus.
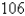 km and apolune altitude
km and apolune altitude 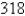 km (above the moon). Find an equation of this ellipse if the radius of the moon is
km (above the moon). Find an equation of this ellipse if the radius of the moon is 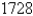 km and the center of the moon is at one focus.
km and the center of the moon is at one focus.
Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
40
Find the point(s) of intersection of the curves and .
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
41
Find an equation of the tangent to the curve at the point corresponding to the given value of the parameter. 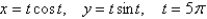
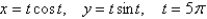

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
42
True or False?
If the parametric curve x = f ( ), y = g ( ) satisfies g '( ) = 0, then it has a horizontal tangent when = .
If the parametric curve x = f ( ), y = g ( ) satisfies g '( ) = 0, then it has a horizontal tangent when = .

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
43
The curve cross itself at some point . Find the equations of both tangent lines at that point.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
44
Find the polar equation for the curve represented by the given Cartesian equation.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
45
Find the exact area of the surface obtained by rotating the given curve about the x-axis.
A)
B)
C)
D)
E) None of these
A)
B)
C)
D)
E) None of these

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
46
Set up, but do not evaluate, an integral that represents the length of the parametric curve. 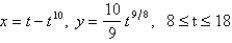
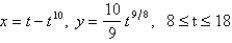

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
47
Find the slope of the tangent line to the given polar curve at the point specified by the value of .
A)
B)
C)
D)
E) 3
A)
B)
C)
D)
E) 3

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
48
Find a polar equation for the curve represented by the given Cartesian equation.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
49
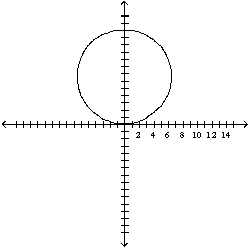
Find the area that the curve encloses. 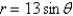
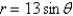


Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
50
Sketch the polar curve with the given equation.
A)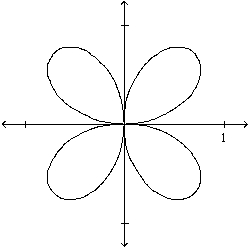
B)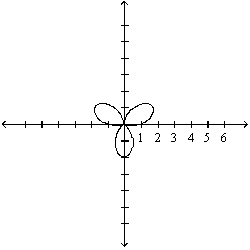
C)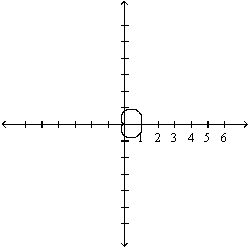
D)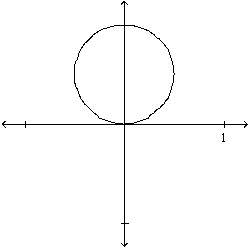
A)

B)

C)

D)


Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
51
Find the length of the curve. , ,
A)
B)
C)
D)
E) None of these
A)
B)
C)
D)
E) None of these

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
52
Find an equation of the tangent line to the curve at the point corresponding to the value of the parameter. 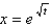 ,
, 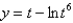 ;
; 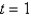
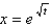 ,
, 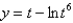 ;
; 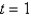

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
53
Find a Cartesian equation for the curve described by the given polar equation. 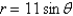
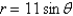

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
54
Find the point(s) on the curve where the tangent is horizontal.
A)
B)
C)
D)
E) None of these
A)
B)
C)
D)
E) None of these

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
55
Find 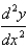 .
. 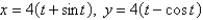
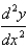 .
. 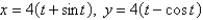

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
56
Find an equation of the tangent to the curve at the point by first eliminating the parameter. 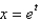 ,
, 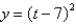 ;
; 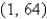
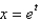 ,
, 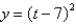 ;
; 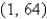

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
57
Find the area enclosed by the curve 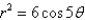 .
.
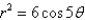 .
.
Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
58
Set up an integral that represents the area of the surface obtained by rotating the given curve about the x-axis. Then use your calculator to find the surface area correct to four decimal places. 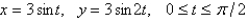
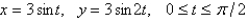

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
59
Find an equation of the tangent to the curve at the point corresponding to the given value of the parameter.
A)
B)
C)
D)
E) None of these
A)
B)
C)
D)
E) None of these

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
60
Set up an integral that represents the length of the curve. Then use your calculator to find the length correct to four decimal places. 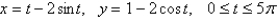
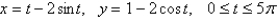

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
61
The exact length of the parametric curve is .

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
62
Find the area bounded by the curve 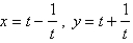 and the line y = 2.5.
and the line y = 2.5.
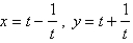 and the line y = 2.5.
and the line y = 2.5.
Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
63
Eliminate the parameter to find a Cartesian equation of the curve. 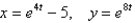
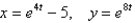

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
64
If a projectile is fired with an initial velocity of meters per second at an angle above the horizontal and air resistance is assumed to be negligible, then its position after t seconds is given by the parametric equations , , where g is the acceleration of gravity . If a gun is fired with and when will the bullet hit the ground?
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
65
Sketch the parametric curve and eliminate the parameter to find the Cartesian equation of the curve. 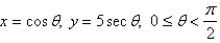
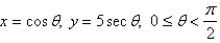

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
66
Eliminate the parameter to find a Cartesian equation of the curve. 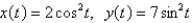
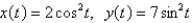

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
67
A cow is tied to a silo with radius 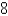 by a rope just long enough to reach the opposite side of the silo. Find the area available for grazing by the cow. Round the answer to the nearest hundredth.
by a rope just long enough to reach the opposite side of the silo. Find the area available for grazing by the cow. Round the answer to the nearest hundredth. 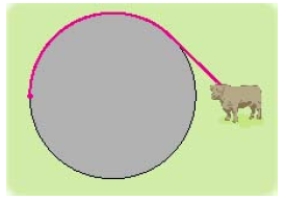
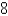 by a rope just long enough to reach the opposite side of the silo. Find the area available for grazing by the cow. Round the answer to the nearest hundredth.
by a rope just long enough to reach the opposite side of the silo. Find the area available for grazing by the cow. Round the answer to the nearest hundredth. 

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
68
Find 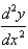 .
. 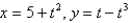
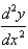 .
. 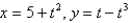

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
69
If a and b are fixed numbers, find parametric equations for the set of all points P determined as shown in the figure, using the angle ang as the parameter. Write the equations for 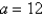 and
and 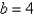 .
. 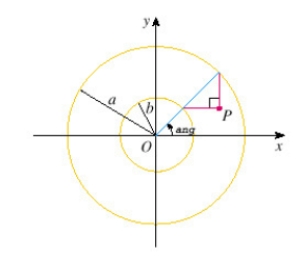
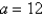 and
and 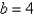 .
. 

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
70
Describe the motion of a particle with position as t varies in the given interval .
A) Moves once counterclockwise along the circle starting and ending at .
B) Moves once counterclockwise along the ellipse starting and ending at .
C) Moves once counterclockwise along the ellipse starting and ending at .
D) Moves once clockwise along the ellipse starting and ending at .
E) Moves once clockwise along the circle starting and ending at .
A) Moves once counterclockwise along the circle starting and ending at .
B) Moves once counterclockwise along the ellipse starting and ending at .
C) Moves once counterclockwise along the ellipse starting and ending at .
D) Moves once clockwise along the ellipse starting and ending at .
E) Moves once clockwise along the circle starting and ending at .

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
71
Find an equation of the tangent to the curve at the point corresponding to the given value of the parameter. 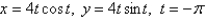
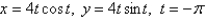

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
72
Find parametric equations to represent the line segment from .
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck
73
Find parametric equations for the path of a particle that moves once clockwise along the circle 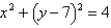 , starting at
, starting at 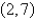 .
.
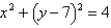 , starting at
, starting at 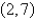 .
.
Unlock Deck
Unlock for access to all 73 flashcards in this deck.
Unlock Deck
k this deck


