Deck 7: Techniques of Integration
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/124
Play
Full screen (f)
Deck 7: Techniques of Integration
1
Evaluate the integral.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)
2
Evaluate the integral if it is convergent. 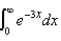
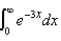
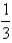
3
Determine whether the improper integral converges or diverges, and if it converges, find its value. 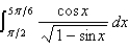
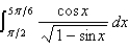
not answered
4
Find the area bounded by the curves and between and .
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
5
Let a and b be real numbers. What integral must appear in place of the question mark "?" to make the following statement true?
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
6
Evaluate the integral or show that it is divergent.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
7
For what values of K is the following integral improper? 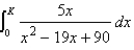
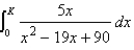

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
8
Determine whether the improper integral converges or diverges, and if it converges, find its value.
A)
B)
C) Diverges
D)
A)
B)
C) Diverges
D)

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
9
Evaluate the integral.
A)
B)
C)
D) 2
E)
A)
B)
C)
D) 2
E)

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
10
Determine whether the improper integral converges or diverges, and if it converges, find its value.
A) 6
B) 0
C) 3
D) Diverges
A) 6
B) 0
C) 3
D) Diverges

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
11
Determine whether the improper integral converges or diverges, and if it converges, find its value.
A)
B)
C)
D) Diverges
A)
B)
C)
D) Diverges

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
12
Determine whether the improper integral converges or diverges, and if it converges, find its value. 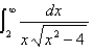
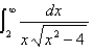

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
13
Determine whether the integral converges or diverges. If it converges, find its value. 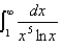
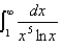

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
14
Use the Trapezoidal Rule to approximate the integral with answers rounded to four decimal places.
A) 0.2029
B) 0.1088
C) 0.1163
D) 0.2326
A) 0.2029
B) 0.1088
C) 0.1163
D) 0.2326

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
15
Evaluate the integral. 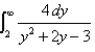
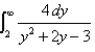

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
16
Evaluate the integral or show that it is divergent. 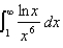
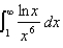

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
17
A manufacturer of light bulbs wants to produce bulbs that last about hours but, of course, some bulbs burn out faster than others. Let be the fraction of the company's bulbs that burn out before t hours. lies between 0 and 1. Let . What is the value of ?
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
18
The region is represented below. Find the area of this region to two decimal places. 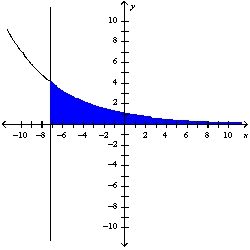
A) 20.28
B)
C)
D)
E)

A) 20.28
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
19
Determine whether the improper integral converges or diverges, and if it converges, find its value.
A) Diverges
B) 0
C) 2
D) 4
A) Diverges
B) 0
C) 2
D) 4

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
20
Determine whether the improper integral converges or diverges, and if it converges, find its value.
A) Diverges
B)
C)
D) 0
A) Diverges
B)
C)
D) 0

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
21
A body moves along a coordinate line in such a way that its velocity at any time t, where 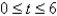 , is given by
, is given by 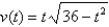 .
.
Find its position function if it is initially located at the origin.
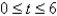 , is given by
, is given by 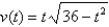 .
.Find its position function if it is initially located at the origin.

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
22
Find a bound on the error in approximating the integral using (a) the Trapezoidal Rule and (b) Simpson's Rule with n subintervals. 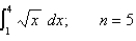
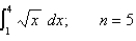

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
23
Use the Table of Integrals to evaluate the integral.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
24
The region under the curve , is rotated about the x-axis. Find the volume of the resulting solid.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
25
Estimate the area of the shaded region by using the Trapezoidal Rule with 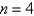 . Round the answer to the nearest tenth.
. Round the answer to the nearest tenth. 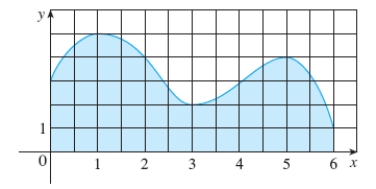
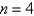 . Round the answer to the nearest tenth.
. Round the answer to the nearest tenth. 

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
26
Find a bound on the error in approximating the integral using (a) the Trapezoidal Rule and (b) Simpson's Rule with n subintervals. 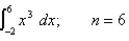
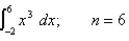

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
27
Use the Trapezoidal Rule to approximate 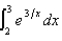 for
for 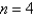 . Round the result to four decimal places.
. Round the result to four decimal places.
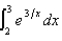 for
for 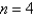 . Round the result to four decimal places.
. Round the result to four decimal places.
Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
28
Use (a) the Trapezoidal Rule and (b) Simpson's Rule to approximate the integral to four decimal places. Compare your results with the exact value. 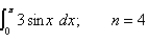
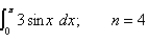

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
29
Use the Midpoint Rule to approximate the given integral with the specified value of n. Compare your result to the actual value. Find the error in the approximation.
A)
B)
C) 0.00008
D) 1.00008
E)
A)
B)
C) 0.00008
D) 1.00008
E)

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
30
Use Simpson's Rule to approximate the integral with answers rounded to four decimal places.
A) 4.0689
B) 3.3296
C) 2.9599
D) 3.6993
A) 4.0689
B) 3.3296
C) 2.9599
D) 3.6993

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
31
Use a table of integrals to evaluate the integral.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
32
Use a table of integrals to evaluate the integral.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
33
Use a table of integrals to evaluate the integral.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
34
Find a bound on the error in approximating the integral using (a) the Trapezoidal Rule and (b) Simpson's Rule with n subintervals. 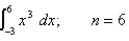
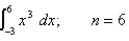

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
35
Eight milligrams of a dye are injected into a vein leading the an individual's heart. The concentration of dye in the aorta (in milligrams per liter) measured at 2-sec intervals is shown in the accompanying table. Use Simpson's Rule with 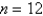 and the formula
and the formula 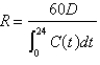 to estimate the person's cardiac output, where D is the quantity of dye injected in milligrams,
to estimate the person's cardiac output, where D is the quantity of dye injected in milligrams, 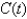 is the concentration of the dye in the aorta, and R is measured in liters per minute. Round to one decimal place.
is the concentration of the dye in the aorta, and R is measured in liters per minute. Round to one decimal place.
t
0
2
4
6
8
10
12
14
16
18
20
22
24
C(t)
0
0
2.6
6.3
9.7
7.5
4.5
3.5
2.2
0.6
0.3
0.1
0
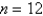 and the formula
and the formula 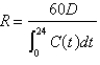 to estimate the person's cardiac output, where D is the quantity of dye injected in milligrams,
to estimate the person's cardiac output, where D is the quantity of dye injected in milligrams, 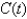 is the concentration of the dye in the aorta, and R is measured in liters per minute. Round to one decimal place.
is the concentration of the dye in the aorta, and R is measured in liters per minute. Round to one decimal place.t
0
2
4
6
8
10
12
14
16
18
20
22
24
C(t)
0
0
2.6
6.3
9.7
7.5
4.5
3.5
2.2
0.6
0.3
0.1
0

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
36
Use the Trapezoidal Rule to approximate the integral with answers rounded to four decimal places.
A) 0.8528
B) 0.9842
C) 0.4921
D) 0.4695
A) 0.8528
B) 0.9842
C) 0.4921
D) 0.4695

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
37
Use Simpson's Rule to approximate the integral with answers rounded to four decimal places.
A) 2.2028
B) 2.7519
C) 3.0265
D) 2.4774
A) 2.2028
B) 2.7519
C) 3.0265
D) 2.4774

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
38
Find a bound on the error in approximating the integral 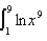 using (a) the Trapezoidal Rule and (b) Simpson's Rule with
using (a) the Trapezoidal Rule and (b) Simpson's Rule with 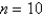 subintervals.
subintervals.
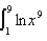 using (a) the Trapezoidal Rule and (b) Simpson's Rule with
using (a) the Trapezoidal Rule and (b) Simpson's Rule with 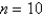 subintervals.
subintervals.
Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
39
Use Simpson's Rule to approximate the integral with answers rounded to four decimal places.
A) 2.0076
B) 2.9504
C) 2.6098
D) 2.2955
A) 2.0076
B) 2.9504
C) 2.6098
D) 2.2955

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
40
Use the Table of Integrals to evaluate the integral.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
41
Use the Table of Integrals to evaluate the integral to three decimal places. 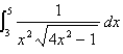
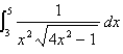

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
42
Evaluate the integral.
A)
B)
C) 0
D)
E)
A)
B)
C) 0
D)
E)

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
43
Evaluate the integral. 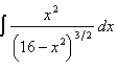
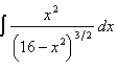

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
44
Evaluate the integral.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
45
Evaluate the integral. 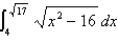
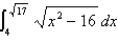

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
46
Write the form of the partial fraction decomposition of the rational expression. Do not find the numerical values of the constants.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
47
Evaluate the integral. 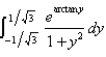
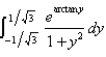

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
48
Find the integral.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
49
Use long division to evaluate the integral.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
50
Evaluate the integral. 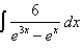
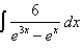

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
51
Find the integral.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
52
Use the Table of Integrals to evaluate the integral. 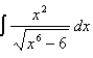
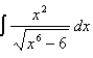

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
53
Evaluate the integral. 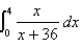
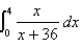

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
54
Find the integral.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
55
Evaluate the integral. 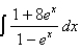
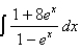

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
56
Find the integral.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
57
Use a table of integrals to evaluate the integral.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
58
Evaluate the integral.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
59
Evaluate the integral. 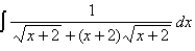
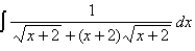

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
60
Use a table of integrals to evaluate the integral.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
61
Find the integral.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
62
Find the integral using an appropriate trigonometric substitution.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
63
Make a substitution to express the integrand as a rational function and then evaluate the integral. 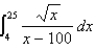 Round the answer to four decimal places.
Round the answer to four decimal places.
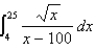 Round the answer to four decimal places.
Round the answer to four decimal places.
Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
64
Evaluate the integral using the indicated trigonometric substitution. 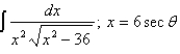
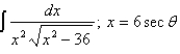

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
65
Find the integral using an appropriate trigonometric substitution.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
66
Evaluate the integral.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
67
Find the integral. 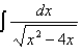
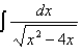

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
68
Find the volume of the resulting solid if the region under the curve 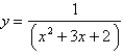 from
from 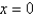 to
to 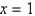 is rotated about the x-axis. Round your answer to four decimal places.
is rotated about the x-axis. Round your answer to four decimal places.
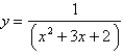 from
from 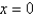 to
to 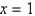 is rotated about the x-axis. Round your answer to four decimal places.
is rotated about the x-axis. Round your answer to four decimal places.
Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
69
Find the integral using an appropriate trigonometric substitution.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
70
Evaluate the integral using the indicated trigonometric substitution.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
71
Use long division to evaluate the integral. The choices are rounded to 3 decimal places.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
72
Find the integral. 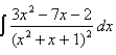
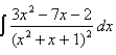

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
73
The region under the graph of ![The region under the graph of on the interval [1, 2] is revolved about the x-axis. Find the volume of the resulting solid.](https://storage.examlex.com/TB5972/11eaa3fc_bf3c_a46f_b1e4_5d06b53d3a5b_TB5972_11.jpg) on the interval [1, 2] is revolved about the x-axis. Find the volume of the resulting solid.
on the interval [1, 2] is revolved about the x-axis. Find the volume of the resulting solid.
![The region under the graph of on the interval [1, 2] is revolved about the x-axis. Find the volume of the resulting solid.](https://storage.examlex.com/TB5972/11eaa3fc_bf3c_a46f_b1e4_5d06b53d3a5b_TB5972_11.jpg) on the interval [1, 2] is revolved about the x-axis. Find the volume of the resulting solid.
on the interval [1, 2] is revolved about the x-axis. Find the volume of the resulting solid.
Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
74
A corporation is building a complex of homes, offices, stores, schools, and churches in a rural community. As a result of this development, the planners have estimated that the community's population (in thousands) t years from now will be given by 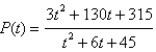 .
.
What will the average population of the community be over the next 10 years?
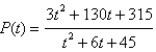 .
.What will the average population of the community be over the next 10 years?

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
75
Evaluate the integral using an appropriate trigonometric substitution.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
76
Evaluate the integral.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
77
Find the integral using an appropriate trigonometric substitution.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
78
Evaluate the integral. 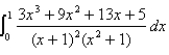
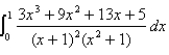

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
79
Eight milligrams of a dye are injected into a vein leading the an individual's heart. The concentration of dye in the aorta (in milligrams per liter) measured at 2-sec intervals is shown in the accompanying table. Use Simpson's Rule with 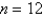 and the formula
and the formula 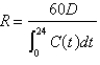 to estimate the person's cardiac output, where D is the quantity of dye injected in milligrams,
to estimate the person's cardiac output, where D is the quantity of dye injected in milligrams, 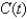 is the concentration of the dye in the aorta, and R is measured in liters per minute. Round your answer to one decimal place.
is the concentration of the dye in the aorta, and R is measured in liters per minute. Round your answer to one decimal place.
t
0
2
4
6
8
10
12
14
16
18
20
22
24
C(t)
0
0
2.6
5.9
9.7
7.9
4.6
3.5
2.2
0.8
0.2
0.1
0
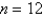 and the formula
and the formula 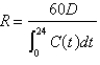 to estimate the person's cardiac output, where D is the quantity of dye injected in milligrams,
to estimate the person's cardiac output, where D is the quantity of dye injected in milligrams, 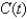 is the concentration of the dye in the aorta, and R is measured in liters per minute. Round your answer to one decimal place.
is the concentration of the dye in the aorta, and R is measured in liters per minute. Round your answer to one decimal place.t
0
2
4
6
8
10
12
14
16
18
20
22
24
C(t)
0
0
2.6
5.9
9.7
7.9
4.6
3.5
2.2
0.8
0.2
0.1
0

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
80
Find the integral. 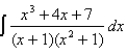
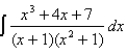

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck


