Deck 5: Applications of Integration
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/70
Play
Full screen (f)
Deck 5: Applications of Integration
1
Evaluate the integral. 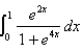
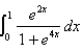
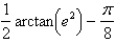
2
Find the general indefinite integral.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)
3
Find the area of the region that lies under the given curve. Round the answer to three decimal places.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)
4
Evaluate the integral by making the given substitution. 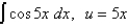
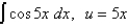

Unlock Deck
Unlock for access to all 70 flashcards in this deck.
Unlock Deck
k this deck
5
Evaluate the integral. 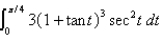
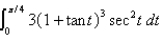

Unlock Deck
Unlock for access to all 70 flashcards in this deck.
Unlock Deck
k this deck
6
Find the area of the region to three decimal places that lies under the given curve.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 70 flashcards in this deck.
Unlock Deck
k this deck
7
Evaluate the integral.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 70 flashcards in this deck.
Unlock Deck
k this deck
8
Evaluate the indefinite integral.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 70 flashcards in this deck.
Unlock Deck
k this deck
9
Evaluate the indefinite integral.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 70 flashcards in this deck.
Unlock Deck
k this deck
10
Evaluate the integral. 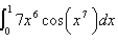
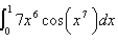

Unlock Deck
Unlock for access to all 70 flashcards in this deck.
Unlock Deck
k this deck
11
Evaluate the integral by making the given substitution.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 70 flashcards in this deck.
Unlock Deck
k this deck
12
Evaluate the integral. 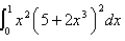
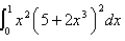

Unlock Deck
Unlock for access to all 70 flashcards in this deck.
Unlock Deck
k this deck
13
Evaluate the definite integral. 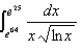
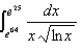

Unlock Deck
Unlock for access to all 70 flashcards in this deck.
Unlock Deck
k this deck
14
Evaluate the integral if it exists.
A) 0
B)
C)
D)
E) none of these
A) 0
B)
C)
D)
E) none of these

Unlock Deck
Unlock for access to all 70 flashcards in this deck.
Unlock Deck
k this deck
15
Evaluate the integral if it exists.
A) 0
B)
C)
D)
E) none of these
A) 0
B)
C)
D)
E) none of these

Unlock Deck
Unlock for access to all 70 flashcards in this deck.
Unlock Deck
k this deck
16
Evaluate the definite integral. 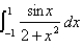
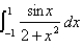

Unlock Deck
Unlock for access to all 70 flashcards in this deck.
Unlock Deck
k this deck
17
Evaluate the indefinite integral. 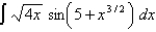
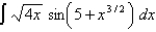

Unlock Deck
Unlock for access to all 70 flashcards in this deck.
Unlock Deck
k this deck
18
Evaluate the indefinite integral.
A)
B)
C)
D)
E) .
A)
B)
C)
D)
E) .

Unlock Deck
Unlock for access to all 70 flashcards in this deck.
Unlock Deck
k this deck
19
Evaluate the indefinite integral. 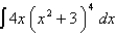
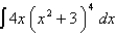

Unlock Deck
Unlock for access to all 70 flashcards in this deck.
Unlock Deck
k this deck
20
Evaluate the indefinite integral.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 70 flashcards in this deck.
Unlock Deck
k this deck
21
Use Part 1 of the Fundamental Theorem of Calculus to find the derivative of the function.
A)
B)
C) none of these
D)
E)
A)
B)
C) none of these
D)
E)

Unlock Deck
Unlock for access to all 70 flashcards in this deck.
Unlock Deck
k this deck
22
The velocity function (in meters per second) is given for a particle moving along a line. Find the distance traveled by the particle during the given time interval.
A) 36 m
B) 72 m
C) 100 m
D) 64 m
E) 68 m
A) 36 m
B) 72 m
C) 100 m
D) 64 m
E) 68 m

Unlock Deck
Unlock for access to all 70 flashcards in this deck.
Unlock Deck
k this deck
23
Find the area of the region that lies to the right of the y-axis and to the left of the parabola 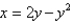 .
.
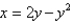 .
.
Unlock Deck
Unlock for access to all 70 flashcards in this deck.
Unlock Deck
k this deck
24
An animal population is increasing at a rate of 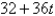 per year (where t is measured in years). By how much does the animal population increase between the fourth and tenth years?
per year (where t is measured in years). By how much does the animal population increase between the fourth and tenth years?
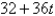 per year (where t is measured in years). By how much does the animal population increase between the fourth and tenth years?
per year (where t is measured in years). By how much does the animal population increase between the fourth and tenth years?
Unlock Deck
Unlock for access to all 70 flashcards in this deck.
Unlock Deck
k this deck
25
Use Part 1 of the Fundamental Theorem of Calculus to find the derivative of the function. 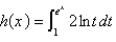
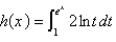

Unlock Deck
Unlock for access to all 70 flashcards in this deck.
Unlock Deck
k this deck
26
An animal population is increasing at a rate of per year (where t is measured in years). By how much does the animal population increase between the fourth and tenth years?
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 70 flashcards in this deck.
Unlock Deck
k this deck
27
Evaluate
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 70 flashcards in this deck.
Unlock Deck
k this deck
28
Estimate the area from 0 to 5 under the graph of using five approximating rectangles and right endpoints.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 70 flashcards in this deck.
Unlock Deck
k this deck
29
The velocity of a car was read from its speedometer at ten-second intervals and recorded in the table. Use the Midpoint Rule to estimate the distance traveled by the car. 0 0
60 54 10 70 20 80 30 90 40 100 50
A) 1.2 miles
B) 1.8 miles
C) 0.8 miles
D) 2.4 miles
E) 0.6 miles
60 54 10 70 20 80 30 90 40 100 50
A) 1.2 miles
B) 1.8 miles
C) 0.8 miles
D) 2.4 miles
E) 0.6 miles

Unlock Deck
Unlock for access to all 70 flashcards in this deck.
Unlock Deck
k this deck
30
The marginal cost of manufacturing x yards of a certain fabric is in dollars per yard. Find the increase in cost if the production level is raised from yards to yards.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 70 flashcards in this deck.
Unlock Deck
k this deck
31
Evaluate the integral.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 70 flashcards in this deck.
Unlock Deck
k this deck
32
The area of the region that lies to the right of the y-axis and to the left of the parabola (the shaded region in the figure) is given by the integral . Find the area.. 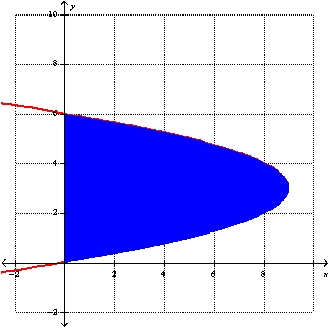
A)
B)
C)
D)
E)

A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 70 flashcards in this deck.
Unlock Deck
k this deck
33
If is a child's rate of growth in pounds per year, which of the following expressions represents the increase in the child's weight (in pounds) between the years 2 and 5 ?
A)
B)
C)
A)
B)
C)

Unlock Deck
Unlock for access to all 70 flashcards in this deck.
Unlock Deck
k this deck
34
If where find .
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 70 flashcards in this deck.
Unlock Deck
k this deck
35
Evaluate the integral if it exists.
A)
B)
C)
D)
E) none of these
A)
B)
C)
D)
E) none of these

Unlock Deck
Unlock for access to all 70 flashcards in this deck.
Unlock Deck
k this deck
36
Evaluate the integral.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 70 flashcards in this deck.
Unlock Deck
k this deck
37
The acceleration function (in m/ ) and the initial velocity are given for a particle moving along a line. Find the velocity at time t and the distance traveled during the given time interval.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 70 flashcards in this deck.
Unlock Deck
k this deck
38
Evaluate the integral.
A) 54
B)
C)
D)
E)
A) 54
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 70 flashcards in this deck.
Unlock Deck
k this deck
39
Evaluate the definite integral.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 70 flashcards in this deck.
Unlock Deck
k this deck
40
Evaluate the integral if it exists. 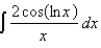
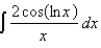

Unlock Deck
Unlock for access to all 70 flashcards in this deck.
Unlock Deck
k this deck
41
Evaluate 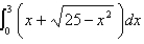 by interpreting it in terms of areas.
by interpreting it in terms of areas.
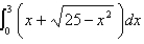 by interpreting it in terms of areas.
by interpreting it in terms of areas.
Unlock Deck
Unlock for access to all 70 flashcards in this deck.
Unlock Deck
k this deck
42
Express the integral as a limit of sums. Then evaluate the limit. 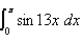
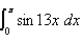

Unlock Deck
Unlock for access to all 70 flashcards in this deck.
Unlock Deck
k this deck
43
Use the Midpoint Rule with n = 10 to approximate the integral.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 70 flashcards in this deck.
Unlock Deck
k this deck
44
Use the given graph of to find the Riemann sum with six subintervals. Take the sample points to be left endpoints. 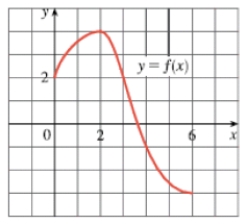
A) 8
B) 6
C) 4
D) 3.5
E) 4.5

A) 8
B) 6
C) 4
D) 3.5
E) 4.5

Unlock Deck
Unlock for access to all 70 flashcards in this deck.
Unlock Deck
k this deck
45
Use the Midpoint Rule with n = 5 to approximate the integral. Round your answer to three decimal places.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 70 flashcards in this deck.
Unlock Deck
k this deck
46
Find the area of the region that lies under the given curve. 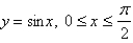
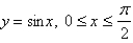

Unlock Deck
Unlock for access to all 70 flashcards in this deck.
Unlock Deck
k this deck
47
Find an expression for the area under the graph of  as a limit. Do not evaluate the limit.
as a limit. Do not evaluate the limit. 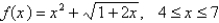
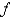 as a limit. Do not evaluate the limit.
as a limit. Do not evaluate the limit. 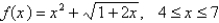

Unlock Deck
Unlock for access to all 70 flashcards in this deck.
Unlock Deck
k this deck
48
Evaluate by interpreting it in terms of areas. 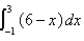
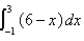

Unlock Deck
Unlock for access to all 70 flashcards in this deck.
Unlock Deck
k this deck
49
Use Part 1 of the Fundamental Theorem of Calculus to find the derivative of the function. 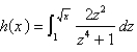
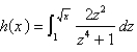

Unlock Deck
Unlock for access to all 70 flashcards in this deck.
Unlock Deck
k this deck
50
Find the derivative of the function. 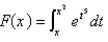
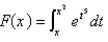

Unlock Deck
Unlock for access to all 70 flashcards in this deck.
Unlock Deck
k this deck
51
Given that 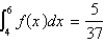 , find
, find 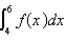 .
.
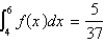 , find
, find 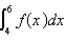 .
.
Unlock Deck
Unlock for access to all 70 flashcards in this deck.
Unlock Deck
k this deck
52
Evaluate the integral. Round your answer to the nearest hundredth.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 70 flashcards in this deck.
Unlock Deck
k this deck
53
Evaluate the Riemann sum for with four subintervals, taking the sample points to be right endpoints.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 70 flashcards in this deck.
Unlock Deck
k this deck
54
Express the limit as a definite integral on the given interval. 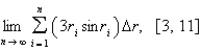
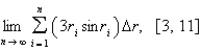

Unlock Deck
Unlock for access to all 70 flashcards in this deck.
Unlock Deck
k this deck
55
Evaluate by interpreting it in terms of areas. 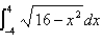
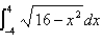

Unlock Deck
Unlock for access to all 70 flashcards in this deck.
Unlock Deck
k this deck
56
If and , find .
A) 6
B) 21
C) 15
D) 9
E)
A) 6
B) 21
C) 15
D) 9
E)

Unlock Deck
Unlock for access to all 70 flashcards in this deck.
Unlock Deck
k this deck
57
A table of values of an increasing function 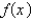 is shown. Use the table to find an upper estimate of
is shown. Use the table to find an upper estimate of 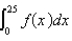 .
. 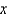
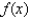
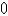 -45
-45 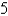 -37
-37 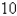 -27
-27 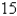 9
9 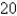 10
10 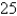 23
23
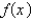 is shown. Use the table to find an upper estimate of
is shown. Use the table to find an upper estimate of 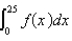 .
. 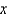
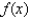
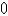 -45
-45 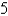 -37
-37 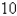 -27
-27 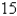 9
9 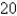 10
10 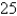 23
23
Unlock Deck
Unlock for access to all 70 flashcards in this deck.
Unlock Deck
k this deck
58
Find the derivative of the function. 


Unlock Deck
Unlock for access to all 70 flashcards in this deck.
Unlock Deck
k this deck
59
Find a function 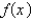 such that
such that 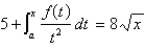 for x > 0 and some number
for x > 0 and some number
a.
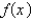 such that
such that 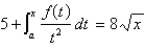 for x > 0 and some number
for x > 0 and some number a.

Unlock Deck
Unlock for access to all 70 flashcards in this deck.
Unlock Deck
k this deck
60
If 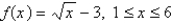 , find the Riemann sum with n = 5 correct to 3 decimal places, taking the sample points to be midpoints.
, find the Riemann sum with n = 5 correct to 3 decimal places, taking the sample points to be midpoints.
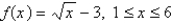 , find the Riemann sum with n = 5 correct to 3 decimal places, taking the sample points to be midpoints.
, find the Riemann sum with n = 5 correct to 3 decimal places, taking the sample points to be midpoints.
Unlock Deck
Unlock for access to all 70 flashcards in this deck.
Unlock Deck
k this deck
61
Use the definition of area to find the area of the region under the graph of f on [a, b] using the indicated choice of ck. ![Use the definition of area to find the area of the region under the graph of f on [a, b] using the indicated choice of c<sub>k</sub>. = + 6x + 1, [ , 1], c<sub>k</sub> is the right endpoint](https://storage.examlex.com/TB5972/11eaa3fc_bfcc_13df_b1e4_f7ba124fcb4c_TB5972_11.jpg) =
= ![Use the definition of area to find the area of the region under the graph of f on [a, b] using the indicated choice of c<sub>k</sub>. = + 6x + 1, [ , 1], c<sub>k</sub> is the right endpoint](https://storage.examlex.com/TB5972/11eaa3fc_bfcc_8910_b1e4_d1374777c29f_TB5972_11.jpg) + 6x + 1, [
+ 6x + 1, [ ![Use the definition of area to find the area of the region under the graph of f on [a, b] using the indicated choice of c<sub>k</sub>. = + 6x + 1, [ , 1], c<sub>k</sub> is the right endpoint](https://storage.examlex.com/TB5972/11eaa3fc_bfcc_b021_b1e4_a996ab6f1277_TB5972_11.jpg) , 1], ck is the right endpoint
, 1], ck is the right endpoint
![Use the definition of area to find the area of the region under the graph of f on [a, b] using the indicated choice of c<sub>k</sub>. = + 6x + 1, [ , 1], c<sub>k</sub> is the right endpoint](https://storage.examlex.com/TB5972/11eaa3fc_bfcc_13df_b1e4_f7ba124fcb4c_TB5972_11.jpg) =
= ![Use the definition of area to find the area of the region under the graph of f on [a, b] using the indicated choice of c<sub>k</sub>. = + 6x + 1, [ , 1], c<sub>k</sub> is the right endpoint](https://storage.examlex.com/TB5972/11eaa3fc_bfcc_8910_b1e4_d1374777c29f_TB5972_11.jpg) + 6x + 1, [
+ 6x + 1, [ ![Use the definition of area to find the area of the region under the graph of f on [a, b] using the indicated choice of c<sub>k</sub>. = + 6x + 1, [ , 1], c<sub>k</sub> is the right endpoint](https://storage.examlex.com/TB5972/11eaa3fc_bfcc_b021_b1e4_a996ab6f1277_TB5972_11.jpg) , 1], ck is the right endpoint
, 1], ck is the right endpoint
Unlock Deck
Unlock for access to all 70 flashcards in this deck.
Unlock Deck
k this deck
62
Find an expression for the area under the graph of 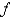 as a limit. Do not evaluate the limit.
as a limit. Do not evaluate the limit. 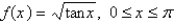
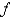 as a limit. Do not evaluate the limit.
as a limit. Do not evaluate the limit. 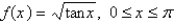

Unlock Deck
Unlock for access to all 70 flashcards in this deck.
Unlock Deck
k this deck
63
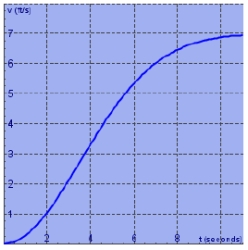
The velocity graph of a car accelerating from rest to a speed of 7 km/h over a period of 10 seconds is shown. Estimate to the nearest integer the distance traveled during this period. Use a right sum with 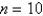 .
. 
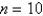 .
. 

Unlock Deck
Unlock for access to all 70 flashcards in this deck.
Unlock Deck
k this deck
64
The velocity graph of a braking car is shown. Use it to estimate to the nearest foot the distance traveled by the car while the brakes are applied.Use a left sum with n = 7. 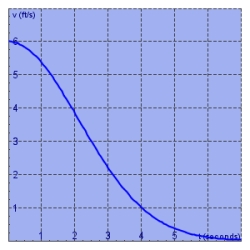


Unlock Deck
Unlock for access to all 70 flashcards in this deck.
Unlock Deck
k this deck
65
Approximate the area under the curve 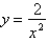 from 1 to 2 using ten approximating rectangles of equal widths and right endpoints. Round the answer to the nearest hundredth.
from 1 to 2 using ten approximating rectangles of equal widths and right endpoints. Round the answer to the nearest hundredth.
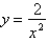 from 1 to 2 using ten approximating rectangles of equal widths and right endpoints. Round the answer to the nearest hundredth.
from 1 to 2 using ten approximating rectangles of equal widths and right endpoints. Round the answer to the nearest hundredth.
Unlock Deck
Unlock for access to all 70 flashcards in this deck.
Unlock Deck
k this deck
66
Approximate the area under the curve from using ten approximating rectangles of equal widths and right endpoints. The choices are rounded to the nearest hundredth.
A) 0.36
B) 0.02
C) 0.72
D) 0.98
E) 1.08
A) 0.36
B) 0.02
C) 0.72
D) 0.98
E) 1.08

Unlock Deck
Unlock for access to all 70 flashcards in this deck.
Unlock Deck
k this deck
67
Determine a region whose area is equal to .
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 70 flashcards in this deck.
Unlock Deck
k this deck
68
By reading values from the given graph of  , use five rectangles to find a lower estimate, to the nearest whole number, for the area from 0 to 10 under the given graph of
, use five rectangles to find a lower estimate, to the nearest whole number, for the area from 0 to 10 under the given graph of  .
. 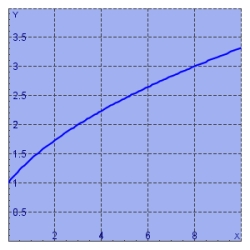
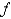 , use five rectangles to find a lower estimate, to the nearest whole number, for the area from 0 to 10 under the given graph of
, use five rectangles to find a lower estimate, to the nearest whole number, for the area from 0 to 10 under the given graph of 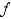 .
. 

Unlock Deck
Unlock for access to all 70 flashcards in this deck.
Unlock Deck
k this deck
69
The speed of a runner increased steadily during the first three seconds of a race. Her speed at half-second intervals is given in the table. Find a lower estimate for the distance that she traveled during these three seconds. 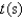
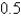
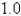
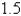
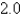
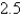
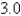
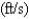
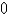 2.8
2.8
3.5
6.9
8.2
12.2
16.3
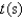
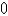
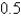
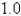
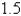
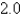
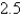
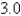
 2.8
2.83.5
6.9
8.2
12.2
16.3

Unlock Deck
Unlock for access to all 70 flashcards in this deck.
Unlock Deck
k this deck
70
Use the definition of area to find the area of the region under the graph of f on [a, b] using the indicated choice of ck. ![Use the definition of area to find the area of the region under the graph of f on [a, b] using the indicated choice of c<sub>k</sub>. = , [0, 2], c<sub>k</sub> is the left endpoint](https://storage.examlex.com/TB5972/11eaa3fc_bfcb_9ead_b1e4_a97c452e3d09_TB5972_11.jpg) =
= ![Use the definition of area to find the area of the region under the graph of f on [a, b] using the indicated choice of c<sub>k</sub>. = , [0, 2], c<sub>k</sub> is the left endpoint](https://storage.examlex.com/TB5972/11eaa3fc_bfcb_c5be_b1e4_7d07a40cd7ac_TB5972_11.jpg) , [0, 2], ck is the left endpoint
, [0, 2], ck is the left endpoint
![Use the definition of area to find the area of the region under the graph of f on [a, b] using the indicated choice of c<sub>k</sub>. = , [0, 2], c<sub>k</sub> is the left endpoint](https://storage.examlex.com/TB5972/11eaa3fc_bfcb_9ead_b1e4_a97c452e3d09_TB5972_11.jpg) =
= ![Use the definition of area to find the area of the region under the graph of f on [a, b] using the indicated choice of c<sub>k</sub>. = , [0, 2], c<sub>k</sub> is the left endpoint](https://storage.examlex.com/TB5972/11eaa3fc_bfcb_c5be_b1e4_7d07a40cd7ac_TB5972_11.jpg) , [0, 2], ck is the left endpoint
, [0, 2], ck is the left endpoint
Unlock Deck
Unlock for access to all 70 flashcards in this deck.
Unlock Deck
k this deck


