Deck 4: Integrals
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/169
Play
Full screen (f)
Deck 4: Integrals
1
Evaluate , and tell whether its antiderivative F is increasing or decreasing at the point radians.
A) - 0.288, increasing
B) 0.757, decreasing
C) , decreasing
D) 0.757, increasing
E) 0.277, decreasing
A) - 0.288, increasing
B) 0.757, decreasing
C) , decreasing
D) 0.757, increasing
E) 0.277, decreasing
, decreasing
2
Given that the graph of f passes through the point (4, 69) and that the slope of its tangent line at is , find f (1) .
A) 0
B) 6
C) 1
D) 11
E) 12
A) 0
B) 6
C) 1
D) 11
E) 12
6
3
Find the most general antiderivative of the function. 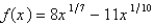
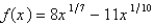
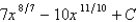
4
Find
f.
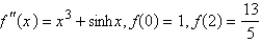
f.
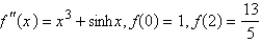

Unlock Deck
Unlock for access to all 169 flashcards in this deck.
Unlock Deck
k this deck
5
Suppose the line 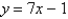 is tangent to the curve
is tangent to the curve 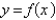 when
when 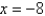 . If Newton's method is used to locate a root of the equation
. If Newton's method is used to locate a root of the equation 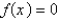 and the initial approximation is
and the initial approximation is 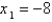 , find the second approximation
, find the second approximation 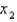 .
.
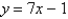 is tangent to the curve
is tangent to the curve 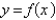 when
when 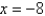 . If Newton's method is used to locate a root of the equation
. If Newton's method is used to locate a root of the equation 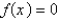 and the initial approximation is
and the initial approximation is 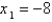 , find the second approximation
, find the second approximation 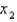 .
.
Unlock Deck
Unlock for access to all 169 flashcards in this deck.
Unlock Deck
k this deck
6
A car braked with a constant deceleration of 40  , producing skid marks measuring 60 ft before coming to a stop. How fast was the car traveling when the brakes were first applied?
, producing skid marks measuring 60 ft before coming to a stop. How fast was the car traveling when the brakes were first applied?
 , producing skid marks measuring 60 ft before coming to a stop. How fast was the car traveling when the brakes were first applied?
, producing skid marks measuring 60 ft before coming to a stop. How fast was the car traveling when the brakes were first applied?
Unlock Deck
Unlock for access to all 169 flashcards in this deck.
Unlock Deck
k this deck
7
A particle is moving with the given data. Find the position of the particle. ,
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 169 flashcards in this deck.
Unlock Deck
k this deck
8
To what constant deceleration would a car moving along a straight road be subjected if the car were brought to rest from a speed of 86 ft/sec in 7 sec? What would the stopping distance be?

Unlock Deck
Unlock for access to all 169 flashcards in this deck.
Unlock Deck
k this deck
9
Find the position function of a particle moving along a coordinate line that satisfies the given conditions. 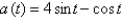 , s (0) = 5, v (0) = 0
, s (0) = 5, v (0) = 0
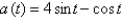 , s (0) = 5, v (0) = 0
, s (0) = 5, v (0) = 0
Unlock Deck
Unlock for access to all 169 flashcards in this deck.
Unlock Deck
k this deck
10
For what values of a and b is 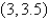 is an inflection point of the curve
is an inflection point of the curve 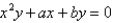 ? What additional inflection points does the curve have?
? What additional inflection points does the curve have?
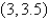 is an inflection point of the curve
is an inflection point of the curve 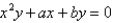 ? What additional inflection points does the curve have?
? What additional inflection points does the curve have?
Unlock Deck
Unlock for access to all 169 flashcards in this deck.
Unlock Deck
k this deck
11
Find the position function of a particle moving along a coordinate line that satisfies the given condition. 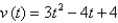 , s(1) = -1
, s(1) = -1
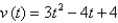 , s(1) = -1
, s(1) = -1
Unlock Deck
Unlock for access to all 169 flashcards in this deck.
Unlock Deck
k this deck
12
Use Newton's method to approximate the indicated root of 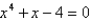 in the interval
in the interval 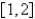 , correct to six decimal places.
, correct to six decimal places.
Use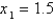 as the initial approximation.
as the initial approximation.
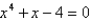 in the interval
in the interval 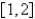 , correct to six decimal places.
, correct to six decimal places.Use
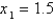 as the initial approximation.
as the initial approximation.
Unlock Deck
Unlock for access to all 169 flashcards in this deck.
Unlock Deck
k this deck
13
Estimate the value of by using three iterations of Newton's method to solve the equation with initial estimate Round your final estimate to four decimal places.
A) 3.3166
B) 2.253
C) 3.2605
D) 2.224
A) 3.3166
B) 2.253
C) 3.2605
D) 2.224

Unlock Deck
Unlock for access to all 169 flashcards in this deck.
Unlock Deck
k this deck
14
Estimate the value of by using three iterations of Newton's method to solve the equation with initial estimate Round your final estimate to four decimal places.
A) 1.71
B) 1.6535
C) 2.2361
D) 2.2662
A) 1.71
B) 1.6535
C) 2.2361
D) 2.2662

Unlock Deck
Unlock for access to all 169 flashcards in this deck.
Unlock Deck
k this deck
15
Find the most general antiderivative of the function. 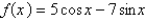
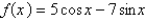

Unlock Deck
Unlock for access to all 169 flashcards in this deck.
Unlock Deck
k this deck
16
What constant acceleration is required to increase the speed of a car from 20 ft/s to 45 ft/s in 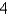 s?
s?
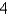 s?
s?
Unlock Deck
Unlock for access to all 169 flashcards in this deck.
Unlock Deck
k this deck
17
Use Newton's method with the specified initial approximation 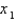 to find
to find 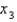 , the third approximation to the root of the given equation. (Give your answer to four decimal places.)
, the third approximation to the root of the given equation. (Give your answer to four decimal places.) 
 to find
to find  , the third approximation to the root of the given equation. (Give your answer to four decimal places.)
, the third approximation to the root of the given equation. (Give your answer to four decimal places.) 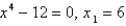

Unlock Deck
Unlock for access to all 169 flashcards in this deck.
Unlock Deck
k this deck
18
A ballast is dropped from a stationary hot-air balloon that is at an altitude of 256 ft. Find (a) an expression for the altitude of the ballast after t seconds, (b) the time when it strikes the ground, and (c) its velocity when it strikes the ground. (Disregard air resistance and take 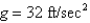 .)
.)
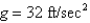 .)
.)
Unlock Deck
Unlock for access to all 169 flashcards in this deck.
Unlock Deck
k this deck
19
Find the most general antiderivative of the function.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 169 flashcards in this deck.
Unlock Deck
k this deck
20
Use Newton's method to obtain an approximation to the root of to within 0.00001.
A) 0.20844
B) 0.2443
C) 0.22413
D) 0.2712
A) 0.20844
B) 0.2443
C) 0.22413
D) 0.2712

Unlock Deck
Unlock for access to all 169 flashcards in this deck.
Unlock Deck
k this deck
21
A manufacturer has been selling 1,200 television sets a week at $400 each. A market survey indicates that for each $30 rebate offered to the buyer, the number of sets sold will increase by 60 per week. Find the demand function.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 169 flashcards in this deck.
Unlock Deck
k this deck
22
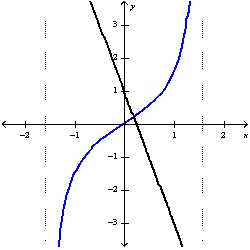
Use Newton's method to find the point of intersection of the graphs of 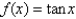 and
and 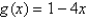 to within 0.00001 by solving the equation
to within 0.00001 by solving the equation 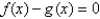 using
using 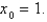
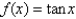 and
and 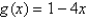 to within 0.00001 by solving the equation
to within 0.00001 by solving the equation 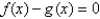 using
using 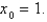


Unlock Deck
Unlock for access to all 169 flashcards in this deck.
Unlock Deck
k this deck
23
Use Newton's method to solve the equation 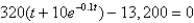 to within 0.00001.
to within 0.00001.
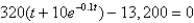 to within 0.00001.
to within 0.00001.
Unlock Deck
Unlock for access to all 169 flashcards in this deck.
Unlock Deck
k this deck
24
An apple orchard has an average yield of 32 bushels of apples per tree if tree density is 30 trees per acre. For each unit increase in tree density, the yield decreases by 2 bushels per tree. How many trees per acre should be planted to maximize yield?
A) 27 trees/acre
B) 30 trees/acre
C) 37 trees/acre
D) 23 trees/acre
A) 27 trees/acre
B) 30 trees/acre
C) 37 trees/acre
D) 23 trees/acre

Unlock Deck
Unlock for access to all 169 flashcards in this deck.
Unlock Deck
k this deck
25
A woman at a point A on the shore of a circular lake with radius wants to arrive at the point C diametrically opposite on the other side of the lake in the shortest possible time. She can walk at the rate of and row a boat at . How should she proceed? (Find ). Round the result, if necessary, to the nearest hundredth. 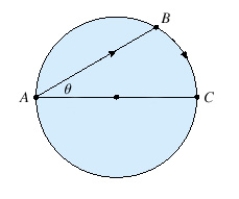
A) radians
B) radians
C) radians
D) She should walk around the lake from point A to point C.
E) She should row from point A to point C radians

A) radians
B) radians
C) radians
D) She should walk around the lake from point A to point C.
E) She should row from point A to point C radians

Unlock Deck
Unlock for access to all 169 flashcards in this deck.
Unlock Deck
k this deck
26
A production editor decided that a promotional flyer should have a 1-in. margin at the top and the bottom, and a -in. margin on each side. The editor further stipulated that the flyer should have an area of 392 . Determine the dimensions of the flyer that will result in the maximum printed area on the flyer. 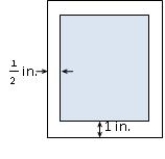
A) 7 in. 56 in.
B) in. in.
C) 14 in. 28 in.
D) in. in.

A) 7 in. 56 in.
B) in. in.
C) 14 in. 28 in.
D) in. in.

Unlock Deck
Unlock for access to all 169 flashcards in this deck.
Unlock Deck
k this deck
27
The sum of two positive numbers is 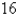 . What is the smallest possible value of the sum of their squares?
. What is the smallest possible value of the sum of their squares?
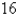 . What is the smallest possible value of the sum of their squares?
. What is the smallest possible value of the sum of their squares?
Unlock Deck
Unlock for access to all 169 flashcards in this deck.
Unlock Deck
k this deck
28
A rectangular beam will be cut from a cylindrical log of radius inches. Suppose that the strength of a rectangular beam is proportional to the product of its width and the square of its depth. Find the dimensions of the strongest beam that can be cut from the cylindrical log. 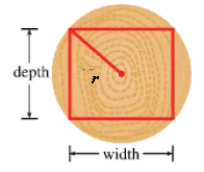
A) in, in
B) in, in
C) in, in
D) in, in
E) in, in

A) in, in
B) in, in
C) in, in
D) in, in
E) in, in

Unlock Deck
Unlock for access to all 169 flashcards in this deck.
Unlock Deck
k this deck
29
Use Newton's method to find the zero of 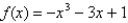 to within 0.00001 by solving the equation
to within 0.00001 by solving the equation 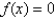 using
using 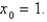
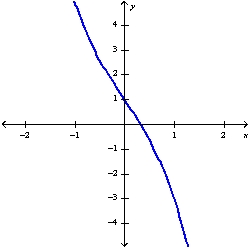
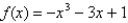 to within 0.00001 by solving the equation
to within 0.00001 by solving the equation 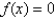 using
using 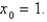


Unlock Deck
Unlock for access to all 169 flashcards in this deck.
Unlock Deck
k this deck
30
What is the shortest possible length of the line segment that is cut off by the first quadrant and is tangent to the curve at some point?
A)
B)
C)
D) None of these
E)
A)
B)
C)
D) None of these
E)

Unlock Deck
Unlock for access to all 169 flashcards in this deck.
Unlock Deck
k this deck
31
Find two positive numbers whose product is and whose sum is a minimum.
A)
B) 3, 48
C) 6, 24
D)
E) 2, 72
A)
B) 3, 48
C) 6, 24
D)
E) 2, 72

Unlock Deck
Unlock for access to all 169 flashcards in this deck.
Unlock Deck
k this deck
32
Use Newton's method to approximate the zero of 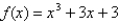 between
between 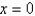 and
and 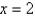 using
using 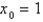 . Continue until two successive approximations differ by less than 0.00001.
. Continue until two successive approximations differ by less than 0.00001.
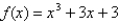 between
between 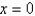 and
and 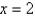 using
using 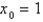 . Continue until two successive approximations differ by less than 0.00001.
. Continue until two successive approximations differ by less than 0.00001.
Unlock Deck
Unlock for access to all 169 flashcards in this deck.
Unlock Deck
k this deck
33
A farmer with 710 ft of fencing wants to enclose a rectangular area and then divide it into four pens with fencing parallel to one side of the rectangle. What is the largest possible total area of the four pens?

Unlock Deck
Unlock for access to all 169 flashcards in this deck.
Unlock Deck
k this deck
34
A piece of wire 10 m long is cut into two pieces. One piece is bent into a square and the other is bent into an equilateral triangle. How should the wire be cut for the square so that the total area enclosed is a minimum? Round your answer to the nearest hundredth.
A) 3.25 m
B) 5.35 m
C) 0 m
D) 4.35 m
E) 4.4 m
A) 3.25 m
B) 5.35 m
C) 0 m
D) 4.35 m
E) 4.4 m

Unlock Deck
Unlock for access to all 169 flashcards in this deck.
Unlock Deck
k this deck
35
Approximate the zero of 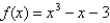 in
in 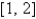 to within 0.00001.
to within 0.00001.
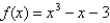 in
in 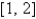 to within 0.00001.
to within 0.00001.
Unlock Deck
Unlock for access to all 169 flashcards in this deck.
Unlock Deck
k this deck
36
Find the dimensions of a rectangle of area 64 that has the smallest possible perimeter.
A) 4 ft by 16 ft
B) 2 ft by 32 ft
C) 1 ft by 64 ft
D) 8 ft by 8 ft
A) 4 ft by 16 ft
B) 2 ft by 32 ft
C) 1 ft by 64 ft
D) 8 ft by 8 ft

Unlock Deck
Unlock for access to all 169 flashcards in this deck.
Unlock Deck
k this deck
37
Find the point on the line that is closest to the origin.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 169 flashcards in this deck.
Unlock Deck
k this deck
38
Find the smallest possible area of an isosceles triangle that is circumscribed about a circle of radius .
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 169 flashcards in this deck.
Unlock Deck
k this deck
39
Find the dimensions of the rectangle enclosed in the semicircle with the largest possible area. 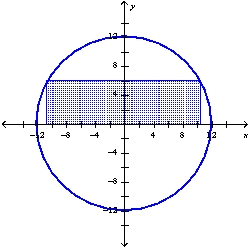
A) 5 in. 7 in.
B) in. in.
C) in. in.
D) in. in.

A) 5 in. 7 in.
B) in. in.
C) in. in.
D) in. in.

Unlock Deck
Unlock for access to all 169 flashcards in this deck.
Unlock Deck
k this deck
40
What is the minimum vertical distance between the parabolas 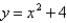 and
and 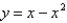 ?
?
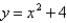 and
and 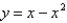 ?
?
Unlock Deck
Unlock for access to all 169 flashcards in this deck.
Unlock Deck
k this deck
41
Find an equation of the line through the point 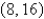 that cuts off the least area from the first quadrant.
that cuts off the least area from the first quadrant.
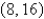 that cuts off the least area from the first quadrant.
that cuts off the least area from the first quadrant.
Unlock Deck
Unlock for access to all 169 flashcards in this deck.
Unlock Deck
k this deck
42
A poster of height 33 in. is mounted on a wall so that its lower edge is 15 in. above the eye level of an observer. How far from the wall should the observer stand so that the viewing angle  subtended at his eye by the poster is as large as possible (see figure - not drawn to scale)?
subtended at his eye by the poster is as large as possible (see figure - not drawn to scale)? 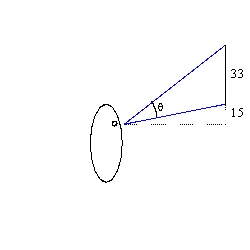 Round your answer to the nearest integer.
Round your answer to the nearest integer.
 subtended at his eye by the poster is as large as possible (see figure - not drawn to scale)?
subtended at his eye by the poster is as large as possible (see figure - not drawn to scale)?  Round your answer to the nearest integer.
Round your answer to the nearest integer.
Unlock Deck
Unlock for access to all 169 flashcards in this deck.
Unlock Deck
k this deck
43
Find the maximum area of a rectangle that can be circumscribed about a given rectangle with length L = 8 and width W = 3. 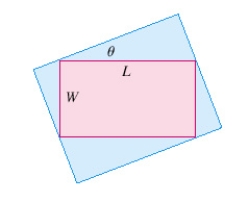


Unlock Deck
Unlock for access to all 169 flashcards in this deck.
Unlock Deck
k this deck
44
A steel pipe is being carried down a hallway 14 ft wide. At the end of the hall there is a right-angled turn into a narrower hallway 6 ft wide. What is the length of the longest pipe that can be carried horizontally around the corner? 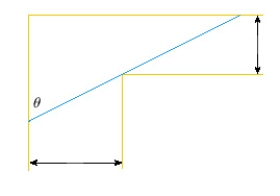


Unlock Deck
Unlock for access to all 169 flashcards in this deck.
Unlock Deck
k this deck
45
a) Graph the funtion . b) Use l'Hospitals' rule to explain the behavior as
A) a)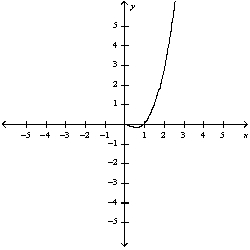 b)
b)
There is a hole at (0, 0)
B)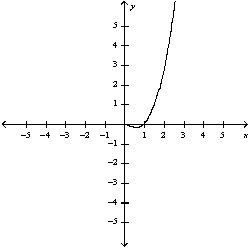 b)
b)
There is a hole at (0, 1)
C)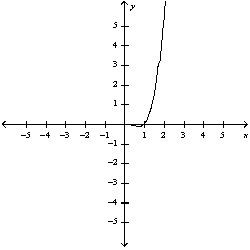 b)
b)
There is a hole at (1, 0)
D)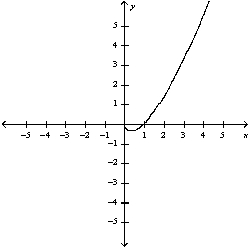 b)
b)
There is a hole at (0, 0)
A) a)
 b)
b) There is a hole at (0, 0)
B)
 b)
b) There is a hole at (0, 1)
C)
 b)
b) There is a hole at (1, 0)
D)
 b)
b) There is a hole at (0, 0)

Unlock Deck
Unlock for access to all 169 flashcards in this deck.
Unlock Deck
k this deck
46
The owner of a ranch has 4000 yd of fencing with which to enclose a rectangular piece of grazing land situated along a straight portion of a river. If fencing is not required along the river, what are the dimensions of the largest area he can enclose? What is the area? 


Unlock Deck
Unlock for access to all 169 flashcards in this deck.
Unlock Deck
k this deck
47
Sketch the curve. ,
A)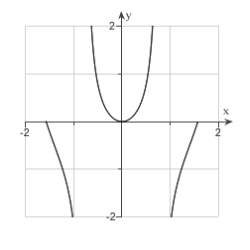
B)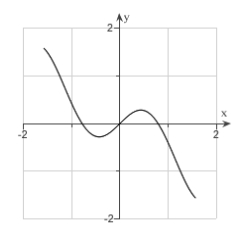
C)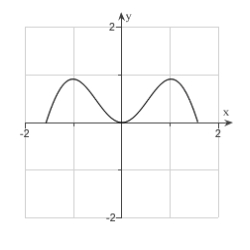
A)

B)

C)


Unlock Deck
Unlock for access to all 169 flashcards in this deck.
Unlock Deck
k this deck
48
For what values of c does the curve have maximum and minimum points?
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 169 flashcards in this deck.
Unlock Deck
k this deck
49
Find the slant asymptote of the function .
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 169 flashcards in this deck.
Unlock Deck
k this deck
50
A rectangular box having a top and a square base is to be constructed at a cost of $1. If the material for the bottom costs $0.35 per square foot, the material for the top costs $0.15 per square foot, and the material for the sides costs $0.20 per square foot, find the dimensions and volume of the box of maximum volume that can be constructed.

Unlock Deck
Unlock for access to all 169 flashcards in this deck.
Unlock Deck
k this deck
51
What can you say about point of inflation for ?
A) point of inflation gets closer to 6
B) point of inflation goes away from the origin
C) point of inflation gets closer to the origin
D) point of inflation goes away from 3
A) point of inflation gets closer to 6
B) point of inflation goes away from the origin
C) point of inflation gets closer to the origin
D) point of inflation goes away from 3

Unlock Deck
Unlock for access to all 169 flashcards in this deck.
Unlock Deck
k this deck
52
Sketch the graph of the function using the curve-sketching guidelines.
A)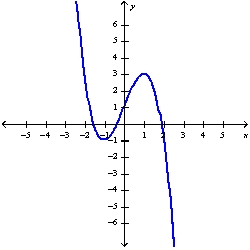
B)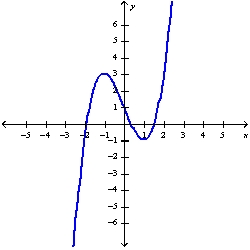
C)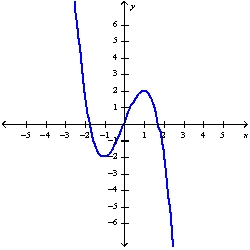
D)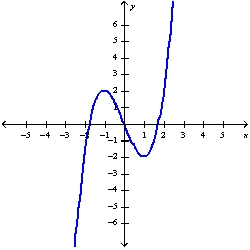
A)

B)

C)

D)


Unlock Deck
Unlock for access to all 169 flashcards in this deck.
Unlock Deck
k this deck
53
What is the function of the graph? 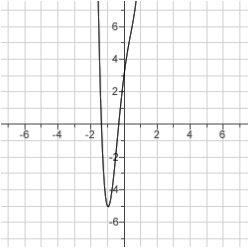
A)
B)
C)
D)
E)

A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 169 flashcards in this deck.
Unlock Deck
k this deck
54
If an open box is made from a metal sheet 9 in. square by cutting out identical squares from each corner an bending up the resulting flaps, determine the dimensions of the box with the largest volume that can be made.

Unlock Deck
Unlock for access to all 169 flashcards in this deck.
Unlock Deck
k this deck
55
Sketch the curve.
A)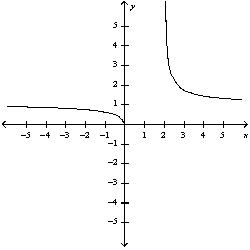
B)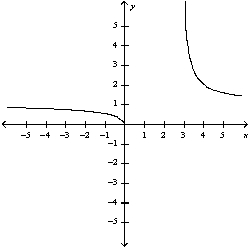
C)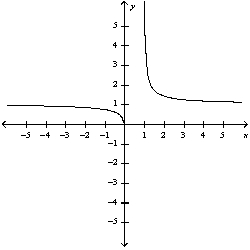
A)

B)

C)


Unlock Deck
Unlock for access to all 169 flashcards in this deck.
Unlock Deck
k this deck
56
Find two numbers whose difference is 170 and whose product is a minimum.

Unlock Deck
Unlock for access to all 169 flashcards in this deck.
Unlock Deck
k this deck
57
Sketch the graph of the function using the curve-sketching guidelines.
A)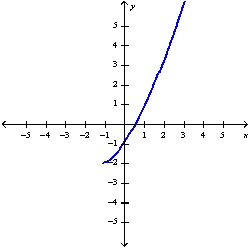
B)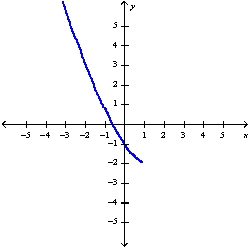
C)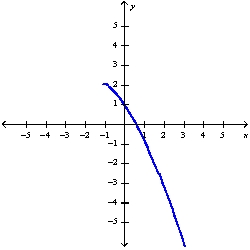
D)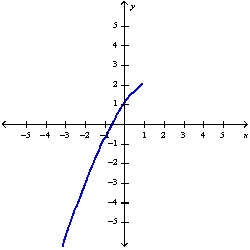
A)
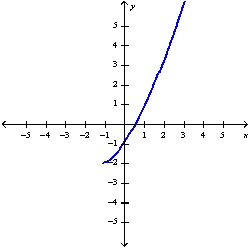
B)

C)
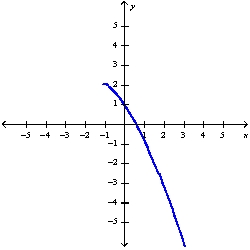
D)
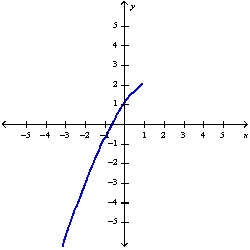

Unlock Deck
Unlock for access to all 169 flashcards in this deck.
Unlock Deck
k this deck
58
Sketch the curve.
A)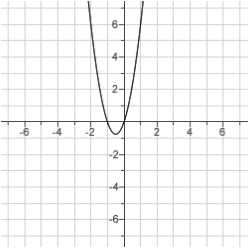
B)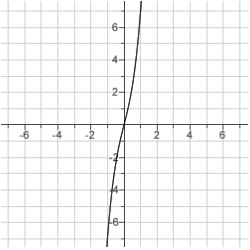
C)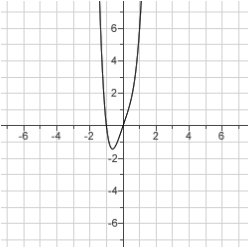
A)

B)

C)


Unlock Deck
Unlock for access to all 169 flashcards in this deck.
Unlock Deck
k this deck
59
The average cost of producing x units of a commodity is given by the equation 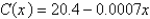 .
.
Find the marginal cost at a production level of 1,255 units.
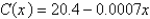 .
.Find the marginal cost at a production level of 1,255 units.

Unlock Deck
Unlock for access to all 169 flashcards in this deck.
Unlock Deck
k this deck
60
Identify any transitional values of at which the basic shape of the curve changes.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 169 flashcards in this deck.
Unlock Deck
k this deck
61
Sketch the graph of the function 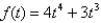 using the curve-sketching guidelines.
using the curve-sketching guidelines.
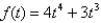 using the curve-sketching guidelines.
using the curve-sketching guidelines.
Unlock Deck
Unlock for access to all 169 flashcards in this deck.
Unlock Deck
k this deck
62
Sketch the curve. Find the equation of the slant asymptote. 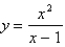
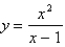

Unlock Deck
Unlock for access to all 169 flashcards in this deck.
Unlock Deck
k this deck
63
Sketch the graph of the function 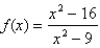 using the curve-sketching guidelines.
using the curve-sketching guidelines.
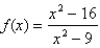 using the curve-sketching guidelines.
using the curve-sketching guidelines.
Unlock Deck
Unlock for access to all 169 flashcards in this deck.
Unlock Deck
k this deck
64
A skydiver leaps from a helicopter hovering high above the ground. Her velocity t sec later and before deploying her parachute is given by where is measured in meters per second. What is her terminal velocity? Hint: Evaluate
A) 54 m/sec
B) 7 m/sec
C) 47 m/sec
D) 87 m/sec
A) 54 m/sec
B) 7 m/sec
C) 47 m/sec
D) 87 m/sec

Unlock Deck
Unlock for access to all 169 flashcards in this deck.
Unlock Deck
k this deck
65
Evaluate the limit using l'Hôpital's Rule.
A) 3
B)
C)
D) 0
A) 3
B)
C)
D) 0

Unlock Deck
Unlock for access to all 169 flashcards in this deck.
Unlock Deck
k this deck
66
Sketch the graph of the function 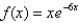 using the curve-sketching guidelines.
using the curve-sketching guidelines.
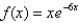 using the curve-sketching guidelines.
using the curve-sketching guidelines.
Unlock Deck
Unlock for access to all 169 flashcards in this deck.
Unlock Deck
k this deck
67
Find the limit.
A)
B) -
C)
D)
A)
B) -
C)
D)

Unlock Deck
Unlock for access to all 169 flashcards in this deck.
Unlock Deck
k this deck
68
Sketch the graph of the function using the curve-sketching guidelines.
A)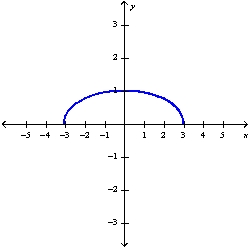
B)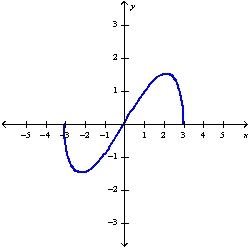
C)
D)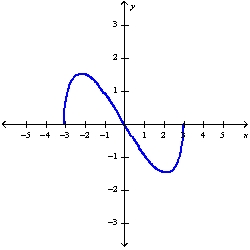
A)

B)

C)

D)


Unlock Deck
Unlock for access to all 169 flashcards in this deck.
Unlock Deck
k this deck
69
Sketch the graph of the function 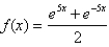 using the curve-sketching guidelines.
using the curve-sketching guidelines.
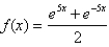 using the curve-sketching guidelines.
using the curve-sketching guidelines.
Unlock Deck
Unlock for access to all 169 flashcards in this deck.
Unlock Deck
k this deck
70
Sketch the graph of the function 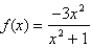 using the curve-sketching guidelines.
using the curve-sketching guidelines.
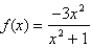 using the curve-sketching guidelines.
using the curve-sketching guidelines.
Unlock Deck
Unlock for access to all 169 flashcards in this deck.
Unlock Deck
k this deck
71
Sketch the graph of the function using the curve-sketching guidelines.
A)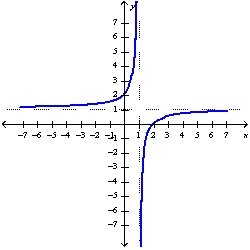
B)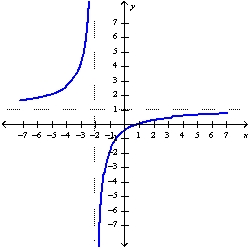
C)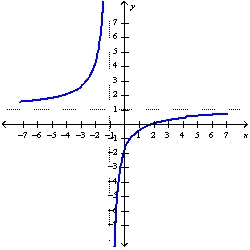
D)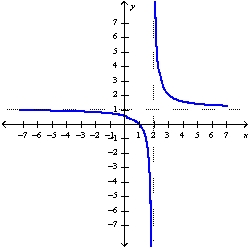
A)

B)

C)

D)


Unlock Deck
Unlock for access to all 169 flashcards in this deck.
Unlock Deck
k this deck
72
Evaluate the limit using l'Hôpital's Rule.
A) 25
B) 0
C) 75
D) 15
A) 25
B) 0
C) 75
D) 15

Unlock Deck
Unlock for access to all 169 flashcards in this deck.
Unlock Deck
k this deck
73
Let P (x) and Q (x) be polynomials. Find if the degree of P (x) is 3 and the degree of Q (x) is 7.
A) - 4
B) 5
C) 9
D) 0
E) 4
A) - 4
B) 5
C) 9
D) 0
E) 4

Unlock Deck
Unlock for access to all 169 flashcards in this deck.
Unlock Deck
k this deck
74
Find the slant asymptote of the graph of using the curve-sketching guidelines.
A)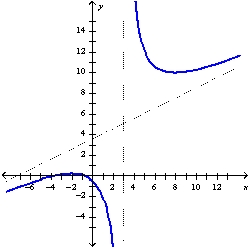
B)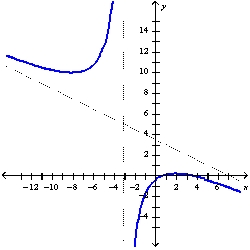
C)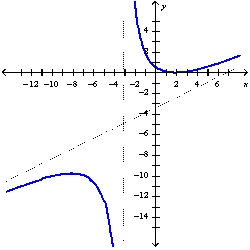
D)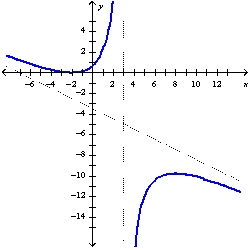
A)

B)

C)

D)


Unlock Deck
Unlock for access to all 169 flashcards in this deck.
Unlock Deck
k this deck
75
An efficiency study showed that the total number of cell phones assembled by the average worker at a manufacturing company t hours after starting work at 8
a.m. is given by
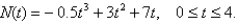
Sketch the graph of the function N, and interpret your result.
a.m. is given by
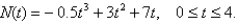
Sketch the graph of the function N, and interpret your result.

Unlock Deck
Unlock for access to all 169 flashcards in this deck.
Unlock Deck
k this deck
76
Find the limit.
A) 0
B)
C)
D)
E) 1
A) 0
B)
C)
D)
E) 1

Unlock Deck
Unlock for access to all 169 flashcards in this deck.
Unlock Deck
k this deck
77
Find the limit.
A) -
B)
C)
D)
A) -
B)
C)
D)

Unlock Deck
Unlock for access to all 169 flashcards in this deck.
Unlock Deck
k this deck
78
Find the limit.
A)
B)
C) 0
D)
A)
B)
C) 0
D)

Unlock Deck
Unlock for access to all 169 flashcards in this deck.
Unlock Deck
k this deck
79
Sketch the graph of the function using the curve-sketching guidelines.
A)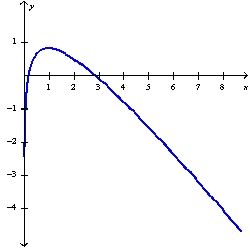
B)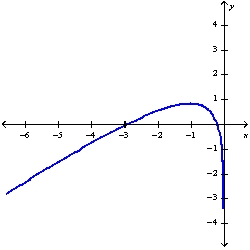
C)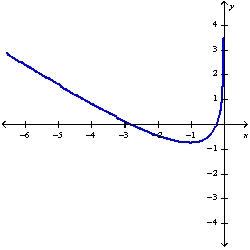
D)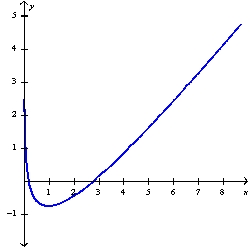
A)

B)

C)

D)


Unlock Deck
Unlock for access to all 169 flashcards in this deck.
Unlock Deck
k this deck
80
Evaluate the limit using l'Hôpital's Rule.
A) ( )
B) 1
C) e
D) 0
A) ( )
B) 1
C) e
D) 0

Unlock Deck
Unlock for access to all 169 flashcards in this deck.
Unlock Deck
k this deck


