Deck 18: Final Exam
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/44
Play
Full screen (f)
Deck 18: Final Exam
1
Evaluate the integral.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)
2
A piece of wire m long is cut into two pieces. One piece is bent into a square and the other is bent into an equilateral triangle. How should the wire be cut for the square so that the total area enclosed is a minimum? Round your answer to the nearest hundredth.
A) m
B) m
C) m
D) m
E) m
A) m
B) m
C) m
D) m
E) m
m
3
Use implicit differentiation to find an equation of the tangent line to the curve at the given point.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)
4
The acceleration function (in m / ) and the initial velocity are given for a particle moving along a line. Find the velocity at time t and the distance traveled during the given time interval.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
5
Find the average value of the function on the interval . Round your answer to 3 decimal places.
A) 0.288
B) 6.228
C) 0.3
D)
E) 12
A) 0.288
B) 6.228
C) 0.3
D)
E) 12

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
6
Find the length of the curve.
A) 25.05
B) 13.05
C) 36.05
D)
E) None of these
A) 25.05
B) 13.05
C) 36.05
D)
E) None of these

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
7
Determine whether the series is convergent or divergent by expressing as a telescoping sum. If it is convergent, find its sum. .
A)
B) diverges
C)
D)
E)
A)
B) diverges
C)
D)
E)

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
8
Find the volume of the solid obtained by rotating the region bounded by the given curves about the specified axis.
A)
B)
C)
D)
E) None of these
A)
B)
C)
D)
E) None of these

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
9
How would you define in order to make f continuous at ?
A)
B)
C)
D)
E) None of these
A)
B)
C)
D)
E) None of these

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
10
Find the area of the region that lies under the given curve. Round the answer to three decimal places.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
11
Evaluate the integral.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
12
The height (in meters) of a projectile shot vertically upward from a point m above ground level with an initial velocity of 25.48 m/s is after t seconds.
a. When does the projectile reach its maximum height?
b. What is the maximum height?
A)
B)
C)
D)
E)
a. When does the projectile reach its maximum height?
b. What is the maximum height?
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
13
Which equation does the function satisfy?
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
14
If , evaluate the difference quotient .
A)
B)
C) h
D)
E) None of these
A)
B)
C) h
D)
E) None of these

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
15
The graphs of and are given. For what values of x is ? 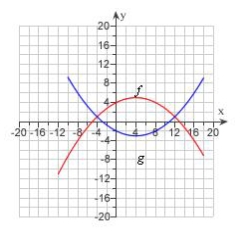
A)
B)
C) -4, 12
D) 0
E) 4, 2

A)
B)
C) -4, 12
D) 0
E) 4, 2

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
16
Find the number c that satisfies the conclusion of the Mean Value Theorem on the given interval. ,
A)
B)
C)
D)
E) None of these
A)
B)
C)
D)
E) None of these

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
17
Solve the initial-value problem.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
18
If an equation of the tangent line to the curve at the point where
A)
B)
C)
D)
E) None of these
A)
B)
C)
D)
E) None of these

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
19
Set up an integral that represents the length of the curve. Then use your calculator to find the length correct to four decimal places.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
20
The masses are located at the point . Find the moments and and the center of mass of the system. ;
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
21
Use spherical coordinates. Evaluate , where is the ball with center the origin and radius .
A)
B)
C)
D)
E) None of these
A)
B)
C)
D)
E) None of these

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
22
Find for the function .
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
23
Find a nonzero vector orthogonal to the plane through the points P, Q, and R.
A)
B)
C)
D)
E) None of these
A)
B)
C)
D)
E) None of these

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
24
Find the unit tangent vector for the curve given by 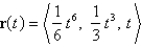 .
.
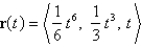 .
.
Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
25
If , evaluate .
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
26
The graphs of 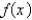 and
and 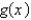 are given.
are given.
Find the values of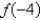 and
and 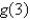 .
. 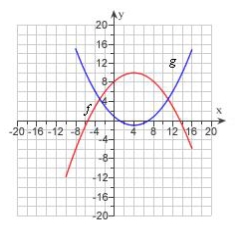
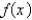 and
and 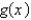 are given.
are given.Find the values of
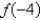 and
and 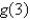 .
. 

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
27
If 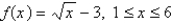 , find the Riemann sum with n = 5 correct to 3 decimal places, taking the sample points to be midpoints.
, find the Riemann sum with n = 5 correct to 3 decimal places, taking the sample points to be midpoints.
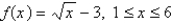 , find the Riemann sum with n = 5 correct to 3 decimal places, taking the sample points to be midpoints.
, find the Riemann sum with n = 5 correct to 3 decimal places, taking the sample points to be midpoints.
Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
28
Find the volume of the resulting solid if the region under the curve 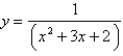 from
from 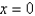 to
to 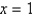 is rotated about the x-axis. Round your answer to four decimal places.
is rotated about the x-axis. Round your answer to four decimal places.
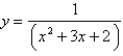 from
from 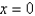 to
to 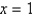 is rotated about the x-axis. Round your answer to four decimal places.
is rotated about the x-axis. Round your answer to four decimal places.
Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
29
Find the sum of the series.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
30
Find the area of the region that is bounded by the given curve and lies in the specified sector. 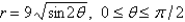

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
31
Solve the initial-value problem. 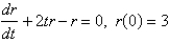

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
32
Evaluate the integral using the indicated trigonometric substitution. 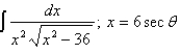
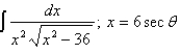

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
33
Find the directional derivative of at the point (1, 3) in the direction toward the point (3, 1).
A)
B)
C)
D)
E) None of these
A)
B)
C)
D)
E) None of these

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
34
Calculate the given quantities if 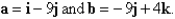
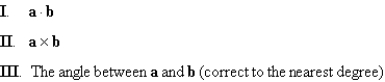
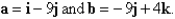
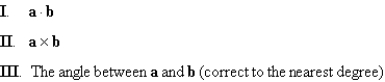

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
35
Find the curvature of .
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
36
Find the local and absolute extreme values of the function on the given interval. 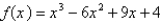 ,
, 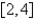
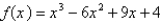 ,
, 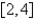

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
37
Use Euler's method with step size 0.1 to estimate  , where
, where 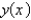 is the solution of the initial-value problem. Round your answer to four decimal places.
is the solution of the initial-value problem. Round your answer to four decimal places. 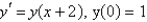
 , where
, where 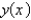 is the solution of the initial-value problem. Round your answer to four decimal places.
is the solution of the initial-value problem. Round your answer to four decimal places. 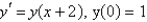

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
38
The top of a ladder slides down a vertical wall at a rate of 0.1m/s . At the moment when the bottom of the ladder is 3 m from the wall, it slides away from the wall at a rate of 0.2 m/s .
How long is the ladder?
How long is the ladder?

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
39
Find the length of the curve. 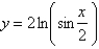 ,
, 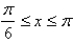
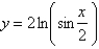 ,
, 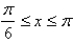

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
40
Evaluate the line integral.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
41
Find the volume of the given solid.
Under the paraboloid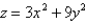 and above the rectangle
and above the rectangle 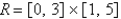 .
.
Under the paraboloid
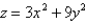 and above the rectangle
and above the rectangle 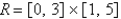 .
.
Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
42
Use Lagrange multipliers to find the maximum and the minimum of f subject to the given constraint(s). 


Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
43
Find the volume of the given solid.
Under the paraboloid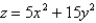 and above the rectangle
and above the rectangle 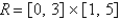 .
.
Under the paraboloid
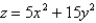 and above the rectangle
and above the rectangle 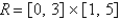 .
.
Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
44
Find all the second partial derivatives of 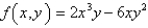
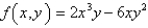

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck


