Deck 11: Infinite Sequences and Series
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/158
Play
Full screen (f)
Deck 11: Infinite Sequences and Series
1
Evaluate the indefinite integral as a power series.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)
2
Given the series estimate the error in using the partial sum by comparison with the series .
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)
3
Find the sum of the series. 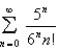
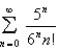
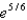
4
Find a power series representation for
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
5
Use multiplication or division of power series to find the first three nonzero terms in the Maclaurin series for the function.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
6
Use series to approximate the definite integral to within the indicated accuracy.
A) 0.0354
B) 0.0125
C) 0.0625
D) 0.1447
E) 0.2774
A) 0.0354
B) 0.0125
C) 0.0625
D) 0.1447
E) 0.2774

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
7
Find the Taylor series for 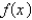 centered at the given value of
centered at the given value of
a. Assume that f has a power series expansion. Also find the associated radius of convergence.
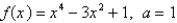
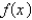 centered at the given value of
centered at the given value of a. Assume that f has a power series expansion. Also find the associated radius of convergence.
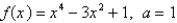

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
8
Use the power series for to estimate correct to four decimal places.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
9
Find the Maclaurin series for f (x) using the definition of the Maclaurin series.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
10
Evaluate the indefinite integral as an infinite series. 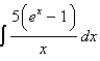
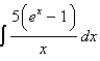

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
11
Use the binomial series to expand the function as a power series. Find the radius of convergence.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
12
Find the Maclaurin series for f and its radius of convergence. 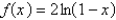
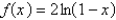

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
13
Use the binomial series to expand the function as a power series. Find the radius of convergence. 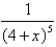
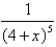

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
14
Use series to evaluate the limit correct to three decimal places. Select the correct answer.
A) 118.933
B) 114.133
C) 34.3233
D) 114.333
E) 115.933
A) 118.933
B) 114.133
C) 34.3233
D) 114.333
E) 115.933

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
15
Find a power series representation for the indefinite integral. 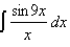
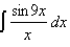

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
16
Find a power series representation for the function.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
17
Find the Maclaurin series for 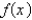 using the definition of a Maclaurin serires.
using the definition of a Maclaurin serires. 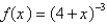
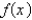 using the definition of a Maclaurin serires.
using the definition of a Maclaurin serires. 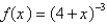

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
18
Find a power series representation for the function and determine the radius of convergence. 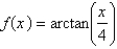
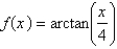

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
19
Evaluate the function by a Taylor polynomial of degree centered at , and .
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
20
Find the radius of convergence and the interval of convergence of the power series.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
21
Find the radius of convergence and the interval of convergence of the power series.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
22
Find the radius of convergence and the interval of convergence of the power series.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
23
Suppose that the radius of convergence of the power series is . What is the radius of convergence of the power series .
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
24
Find the interval of convergence of the series.
A)
B)
C)
D) diverges everywhere
E)
A)
B)
C)
D) diverges everywhere
E)

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
25
Find the interval of convergence of the series. 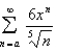
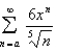

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
26
Test the series for convergence or divergence. 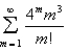
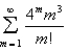

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
27
Find the radius of convergence and the interval of convergence of the power series. 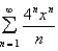
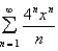

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
28
Find the radius of convergence of the series.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
29
Find the radius of convergence and the interval of convergence of the power series.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
30
Test the series for convergence or divergence. 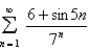
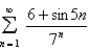

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
31
Determine whether the series is convergent or divergent. 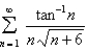
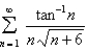

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
32
Find the radius of convergence and the interval of convergence of the power series.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
33
Find the radius of convergence of the series.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
34
Find the radius of convergence and the interval of convergence of the power series. 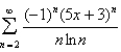
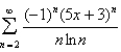

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
35
Determine whether the series converges or diverges. 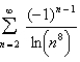
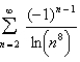

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
36
Test the series for convergence or divergence. 


Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
37
Find the radius of convergence and the interval of convergence of the power series.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
38
Use the binomial series to expand the function as a power series. Find the radius of convergence. 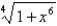
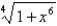

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
39
Determine whether the series is convergent or divergent. 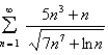
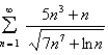

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
40
Find the radius of convergence and the interval of convergence of the power series.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
41
Which of the given series are absolutely convergent?
A)
B)
A)
B)

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
42
Determine whether the series is convergent or divergent. 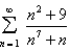
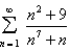

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
43
Determine whether the series converges or diverges. 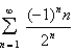
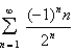

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
44
Determine whether the series is absolutely convergent, conditionally convergent, or divergent.
A) absolutely convergent
B) divergent
C) conditionally convergent
A) absolutely convergent
B) divergent
C) conditionally convergent

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
45
Determine whether the series is absolutely convergent, conditionally convergent, or divergent.
A) absolutely convergent
B) divergent
C) conditionally convergent
A) absolutely convergent
B) divergent
C) conditionally convergent

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
46
Test the series for convergence or divergence. 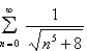
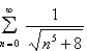

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
47
Use the sum of the first 9 terms to approximate the sum of the following series. 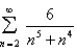 Write your answer to six decimal places.
Write your answer to six decimal places.
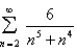 Write your answer to six decimal places.
Write your answer to six decimal places.
Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
48
Determine whether the series is absolutely convergent, conditionally convergent, or divergent. 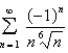
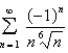

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
49
Determine whether the series converges or diverges. 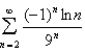
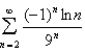

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
50
Find the partial sum of the series . Give your answer to five decimal places.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
51
Determine whether the series is convergent or divergent. 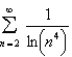
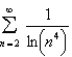

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
52
Determine whether the series converges or diverges. 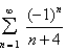
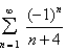

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
53
Test the series for convergence or divergence. 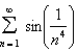
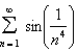

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
54
Determine whether the series is absolutely convergent, conditionally convergent, or divergent. 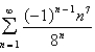
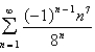

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
55
For which positive integers k is the series convergent?
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
56
Determine whether the series converges or diverges. 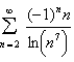
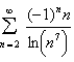

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
57
Determine whether the series converges or diverges. 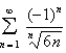
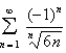

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
58
Determine whether the series converges or diverges. 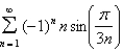
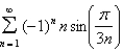

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
59
Determine whether the series is convergent or divergent. 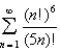
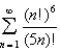

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
60
Determine whether the series is absolutely convergent, conditionally convergent, or divergent. 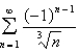
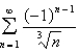

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
61
Approximate the sum to the indicated accuracy. (five decimal places)
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
62
How many terms of the series do we need to add in order to find the sum to the indicated accuracy?
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
63
Determine the number of terms sufficient to obtain the sum of the series accurate to three decimal places.
A) 19
B) 22
C) 20
D) 21
A) 19
B) 22
C) 20
D) 21

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
64
Test the series for convergence or divergence.
A) The series is convergent.
B) The series is divergent.
A) The series is convergent.
B) The series is divergent.

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
65
Find an approximation of the sum of the series accurate to two decimal places.
A) -0.95
B) -1.02
C) -0.87
D) -1.09
A) -0.95
B) -1.02
C) -0.87
D) -1.09

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
66
Approximate the sum to the indicated accuracy. 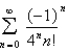
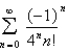

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
67
Which of the partial sums of the alternating series are overestimates of the total sum?
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
68
Test the series for convergence or divergence. 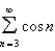
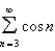

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
69
Let where f is a continuous, positive, and decreasing function on and suppose that is convergent. Defining where and we have that Find the maximum error if the sum of the series is approximated by
A) 0.2
B) 0.025
C) 0.0006
D) 0.005
A) 0.2
B) 0.025
C) 0.0006
D) 0.005

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
70
Use the Comparison Test to determine whether the series is convergent or divergent. 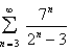
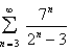

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
71
Use the Alternating Series Estimation Theorem or Taylor's Inequality to estimate the range of values of x for which the given approximation is accurate to within the stated error. 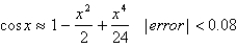 Write a such that
Write a such that 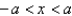 .
.
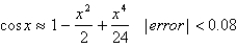 Write a such that
Write a such that 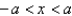 .
.
Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
72
Determine whether the series is convergent or divergent. 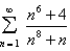
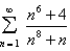

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
73
Test the series for convergence or divergence. 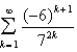
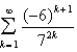

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
74
Test the series for convergence or divergence. 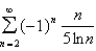
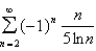

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
75
Determine whether the sequence convergent or divergent.
A) converges
B) diverges
A) converges
B) diverges

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
76
Determine whether the series is convergent or divergent. 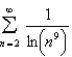
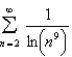

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
77
Determine which series is convergent.
A)
B)
A)
B)

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
78
Approximate the sum to the indicated accuracy. 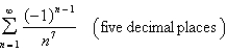
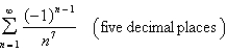

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
79
Determine whether the series is convergent or divergent. 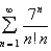
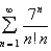

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
80
Determine whether the series is convergent or divergent. 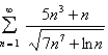
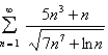

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck


