Deck 12: Vectors and the Geometry of Space
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/60
Play
Full screen (f)
Deck 12: Vectors and the Geometry of Space
1
Classify the surface.
A) A hyperboloid of one sheet with center and axis parallel to the z-axis.
B) A cone with axis parallel to the z-axis and vertex .
C) A circular paraboloid with vertex and axis the z-axis.
A) A hyperboloid of one sheet with center and axis parallel to the z-axis.
B) A cone with axis parallel to the z-axis and vertex .
C) A circular paraboloid with vertex and axis the z-axis.
A cone with axis parallel to the z-axis and vertex .
2
Find an equation for the surface consisting of all points P for which the distance from P to the x-axis is times the distance from P to the yz-plane.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)
3
An ellipsoid is created by rotating the ellipse about the x-axis. Find the equation of the ellipsoid.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)
4
Find an equation of the plane with x-intercept , y-intercept and z-intercept .
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
5
Reduce the equation to one of the standard forms.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
6
Find an equation for the surface obtained by rotating the parabola about the y-axis.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
7
Which of the given lines is parallel to the line
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
8
Find an equation of the set of all points equidistant from the points and
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
9
Find an equation for the surface consisting of all points that are equidistant from the point and the plane .
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
10
Find parametric equations for the line through 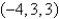 and
and 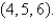
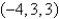 and
and 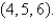

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
11
Find the distance (correct to two decimal places) between the given parallel planes.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
12
Find an equation for the surface obtained by rotating the line 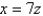 about the x-axis.
about the x-axis.
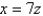 about the x-axis.
about the x-axis.
Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
13
Identify the planes that are perpendicular.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
14
Find the equation of the line through 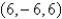 and perpendicular to the plane
and perpendicular to the plane 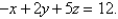
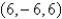 and perpendicular to the plane
and perpendicular to the plane 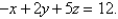

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
15
Find the distance between the point and the plane Round your answer to two decimal place.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
16
Find parametric equations for the line through the point that is parallel to the plane and perpendicular to the line
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
17
Find an equation of the plane that passes through the line of intersection of the planes 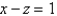 and
and 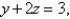 is perpendicular to the plane
is perpendicular to the plane 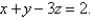
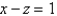 and
and 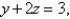 is perpendicular to the plane
is perpendicular to the plane 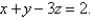

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
18
Find the distance between the planes.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
19
Find, correct to the nearest degree, the angle between the planes.
A)
B)
C)
D)
E) none of these
A)
B)
C)
D)
E) none of these

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
20
Find the point at which the line given by the parametric equations below intersects the plane.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
21
Find the cross product .
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
22
Find an equation of the plane that passes through the point 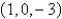 and contains the line
and contains the line 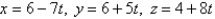
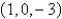 and contains the line
and contains the line 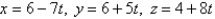

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
23
Find the values of x such that the vectors and are orthogonal.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
24
Calculate the given quantities if 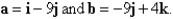
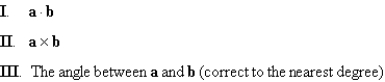
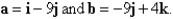
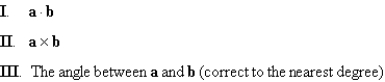

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
25
Find parametric equations for the line through 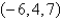 and parallel to the vector
and parallel to the vector 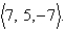
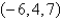 and parallel to the vector
and parallel to the vector 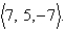

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
26
Find the magnitude of the torque about P correct to two decimal places if a d-lb force is applied as shown. Let 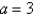 ft,
ft, 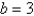 ft,
ft, 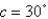 ,
, 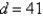 lb.
lb. 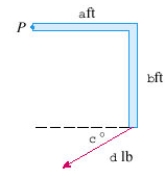
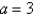 ft,
ft, 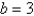 ft,
ft, 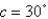 ,
, 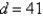 lb.
lb. 

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
27
Velocities have both direction and magnitude and thus are vectors. The magnitude of a velocity vector is called speed. Suppose that a wind is blowing from the direction N 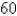
 W at a speed of
W at a speed of 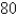 km/h. (This means that the direction from which the wind blows is
km/h. (This means that the direction from which the wind blows is 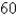
 west of the northerly direction.) A pilot is steering a plane in the direction N
west of the northerly direction.) A pilot is steering a plane in the direction N 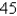
 E at an airspeed (speed in still air) of
E at an airspeed (speed in still air) of 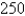 km/h. The true course, or track, of the plane is the direction of the resultant of the velocity vectors of the plane and the wind. The ground speed of the plane is the magnitude of the resultant. Find the ground speed of the plane. Round the result to the nearest hundredth.
km/h. The true course, or track, of the plane is the direction of the resultant of the velocity vectors of the plane and the wind. The ground speed of the plane is the magnitude of the resultant. Find the ground speed of the plane. Round the result to the nearest hundredth.
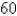
 W at a speed of
W at a speed of 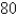 km/h. (This means that the direction from which the wind blows is
km/h. (This means that the direction from which the wind blows is 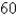
 west of the northerly direction.) A pilot is steering a plane in the direction N
west of the northerly direction.) A pilot is steering a plane in the direction N 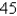
 E at an airspeed (speed in still air) of
E at an airspeed (speed in still air) of 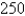 km/h. The true course, or track, of the plane is the direction of the resultant of the velocity vectors of the plane and the wind. The ground speed of the plane is the magnitude of the resultant. Find the ground speed of the plane. Round the result to the nearest hundredth.
km/h. The true course, or track, of the plane is the direction of the resultant of the velocity vectors of the plane and the wind. The ground speed of the plane is the magnitude of the resultant. Find the ground speed of the plane. Round the result to the nearest hundredth.
Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
28
Find the volume of the parallelepiped with adjacent edges PQ, PR, and PS. 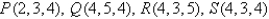
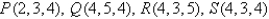

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
29
A bicycle pedal is pushed by a foot with a force of a-N as shown. The shaft of the pedal is  cm long.
cm long.
Find the magnitude of the torque about P correct to two decimal places.
Let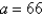 N,
N, 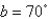 ,
, 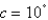 .
. 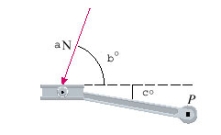
 cm long.
cm long.Find the magnitude of the torque about P correct to two decimal places.
Let
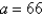 N,
N, 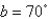 ,
, 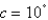 .
. 

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
30
Let and let u be a vector with length that starts at the origin and rotates in the xy - plane. Find the maximum value of the length of the vector .
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
31
Find an equation of the plane through the origin and parallel to the plane 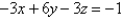
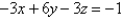

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
32
Find the work done by a force that moves an object from the point to the point along a straight line. The distance is measured in meters and the force in newtons.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
33
Find correct to three decimal places where , , .
A) .
B)
C) .
D)
E)
A) .
B)
C) .
D)
E)

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
34
A woman walks due west on the deck of a ship at 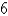 mi/h. The ship is moving north at a speed of
mi/h. The ship is moving north at a speed of 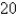 mi/h. Find the speed of the woman relative to the surface of the water. Round the result to the nearest tenth.
mi/h. Find the speed of the woman relative to the surface of the water. Round the result to the nearest tenth.
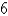 mi/h. The ship is moving north at a speed of
mi/h. The ship is moving north at a speed of 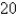 mi/h. Find the speed of the woman relative to the surface of the water. Round the result to the nearest tenth.
mi/h. Find the speed of the woman relative to the surface of the water. Round the result to the nearest tenth.
Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
35
Two forces with magnitudes 8 lb and 12 lb act on an object at a point P as shown in the figure. Find the magnitude of the resultant force F acting at P. Round the result to the nearest tenth. 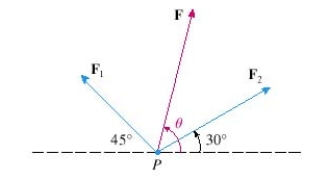
A)
B)
C)
D)
E)

A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
36
Find a nonzero vector orthogonal to the plane through the points P, Q, and R.
A)
B)
C)
D)
E) None of these
A)
B)
C)
D)
E) None of these

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
37
Calculate the angle between a and b (correct to the nearest degree).
A)
B)
C)
D)
E) None of these
A)
B)
C)
D)
E) None of these

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
38
Find the unit vectors that are parallel to the tangent line to the curve at the point .
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
39
Find the point of intersection. 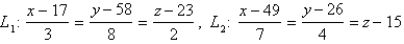
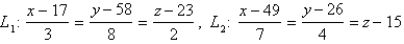

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
40
The tension T at each end of the chain has magnitude 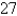 N and makes an angle
N and makes an angle 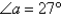 with the horizontal. What is the weight of the chain? Round the result to the nearest hundredth.
with the horizontal. What is the weight of the chain? Round the result to the nearest hundredth. 
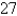 N and makes an angle
N and makes an angle 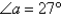 with the horizontal. What is the weight of the chain? Round the result to the nearest hundredth.
with the horizontal. What is the weight of the chain? Round the result to the nearest hundredth. 

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
41
Write an inequality to describe the half-space consisting of all points to the left of a plane parallel to the xz-plane and 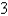 units to the right of it.
units to the right of it.
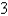 units to the right of it.
units to the right of it.
Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
42
Write inequalities to describe the solid upper hemisphere of the sphere of radius 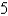 centered at the origin.
centered at the origin.
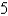 centered at the origin.
centered at the origin.
Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
43
Draw a rectangular box with the origin and 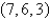 as opposite vertices and with its faces parallel to the coordinate planes. Find the length of the diagonal of the box.
as opposite vertices and with its faces parallel to the coordinate planes. Find the length of the diagonal of the box.
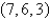 as opposite vertices and with its faces parallel to the coordinate planes. Find the length of the diagonal of the box.
as opposite vertices and with its faces parallel to the coordinate planes. Find the length of the diagonal of the box.
Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
44
Find the midpoint of the line segment joining the given points. (-5, 0, 2) and (-3, -2, 4)
A) ( , , )
B) ( , , )
C) ( , , )
D) ( , , )
A) ( , , )
B) ( , , )
C) ( , , )
D) ( , , )

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
45
Find the length of the median of side AB of the triangle with vertices 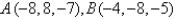
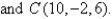
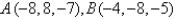
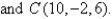

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
46
Find that the midpoint of the line segment from to .
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
47
Find an equation of the sphere with center that touches the xy-plane.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
48
Determine whether the given points are collinear. A (-3, -2, -3), B (-9, -5, 0), and C (-1, -1, -4)
A) Not collinear
B) Collinear
A) Not collinear
B) Collinear

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
49
Find the standard equation of the sphere with center C and radius r. C (3, -5, 3); r = 7
A) (x - 3)2 + (y + 5)2 + (z - 3)2 = 7
B) (x - 3)2 + (y + 5)2 + (z - 3)2 = 49
C) (x + 3)2 + (y - 5)2 + (z + 3)2 = 49
D) (x + 3)2 + (y - 5)2 + (z + 3)2 = 7
A) (x - 3)2 + (y + 5)2 + (z - 3)2 = 7
B) (x - 3)2 + (y + 5)2 + (z - 3)2 = 49
C) (x + 3)2 + (y - 5)2 + (z + 3)2 = 49
D) (x + 3)2 + (y - 5)2 + (z + 3)2 = 7

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
50
Write inequalities to describe the solid rectangular box in the first octant bounded by the
planes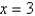 ,
, 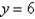 , and
, and 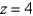 .
.
planes
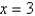 ,
, 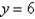 , and
, and 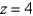 .
.
Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
51
a. Find an equation of the sphere that passes through the point 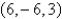 and has center
and has center 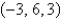 .
.
b. Find the curve in which this sphere intersects the xy-plane.
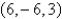 and has center
and has center 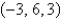 .
. b. Find the curve in which this sphere intersects the xy-plane.

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
52
Plot the given points in a three-dimensional coordinate system. (1, 2, 3)
A)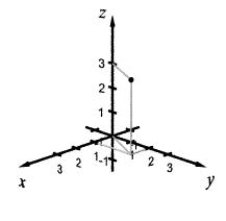
B)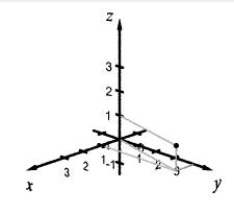
C)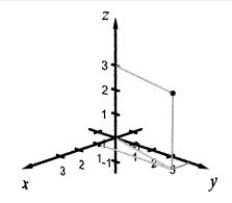
D)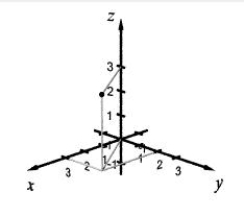
A)

B)

C)

D)


Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
53
Find the length of each side of the triangle ABC and determine whether the triangle is an isosceles triangle, a right triangle, both, or neither. A (-1, 0, 1), B (1, 1, -1), C (1, 1, 1)
A) 1, 1, , both
B) 1, 2, , neither
C) 3, 2, , right
D) 1, 1, , isosceles
A) 1, 1, , both
B) 1, 2, , neither
C) 3, 2, , right
D) 1, 1, , isosceles

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
54
Find an equation of the sphere that passes through the point 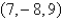 and has center
and has center 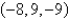 .
.
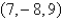 and has center
and has center 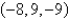 .
.
Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
55
Suppose you start at the origin, move along the x-axis a distance of units in the positive direction, and then move downward a distance of units. What are the coordinates of your position?
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
56
Find the center and radius of the sphere.
A)
B)
C)
D)
E) none of these
A)
B)
C)
D)
E) none of these

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
57
Write an inequality to describe the region consisting of all points between (but not on) the
spheres of radius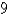 and
and 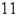 centered at the origin.
centered at the origin.
spheres of radius
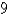 and
and 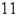 centered at the origin.
centered at the origin.
Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
58
Find the distance from to the xy-planes.
A) 8
B) 16
C) 10
D) 2
E) 4
A) 8
B) 16
C) 10
D) 2
E) 4

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
59
Sketch the plane in a three-dimensional space represented by the equation. z = 2
A)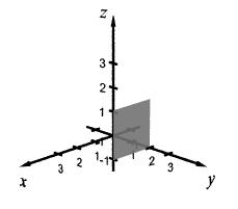
B)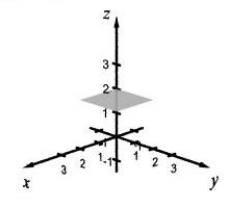
C)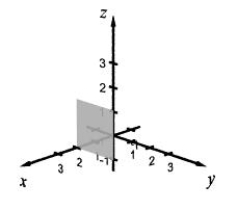
D)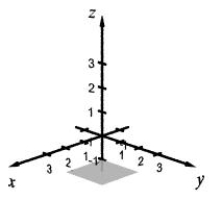
A)

B)

C)

D)


Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
60
Find the center and the radius of the sphere that has the given equation. + + - 6x + 4y = 0
A) ( -3, 2, 0),
B) ( 3, -2, 0), 13
C) ( -3, 2, 0), 13
D) ( 3, -2, 0),
A) ( -3, 2, 0),
B) ( 3, -2, 0), 13
C) ( -3, 2, 0), 13
D) ( 3, -2, 0),

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck


