Deck 6: Continuous Probability Distributions
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/114
Play
Full screen (f)
Deck 6: Continuous Probability Distributions
1
The cumulative distribution function F(x)of a continuous random variable X with the probability density function f(x)is which of the following?
A)The area under f over all values x
B)The area under f over all values that are x or less
C)The area under f over all values that are x or more
D)The area under f over all non-negative values that are x or less
A)The area under f over all values x
B)The area under f over all values that are x or less
C)The area under f over all values that are x or more
D)The area under f over all non-negative values that are x or less
The area under f over all values that are x or less
2
The continuous uniform distribution describes a random variable,defined on the interval [a,b],that has an equally likely chance of assuming values within any subinterval of [a,b] with the same length.
True
3
The probability density function of a continuous uniform distribution is positive for all values between -∞ and +∞.
False
4
A continuous random variable is characterized by uncountable values and can take on any value within an interval.

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
5
Which of the following is correct?
A)A continuous random variable has a probability density function but not a cumulative distribution function.
B)A discrete random variable has a probability mass function but not a cumulative distribution function.
C)A continuous random variable has a probability mass function,and a discrete random variable has a probability density function.
D)A continuous random variable has a probability density function,and a discrete random variable has a probability mass function.
A)A continuous random variable has a probability density function but not a cumulative distribution function.
B)A discrete random variable has a probability mass function but not a cumulative distribution function.
C)A continuous random variable has a probability mass function,and a discrete random variable has a probability density function.
D)A continuous random variable has a probability density function,and a discrete random variable has a probability mass function.

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
6
The standard normal distribution is a normal distribution with a mean equal to zero and a standard deviation equal to one.

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
7
The mean of a continuous uniform distribution is simply the average of the upper and lower limits of the interval on which the distribution is defined.

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
8
Which of the following does not represent a continuous random variable?
A)Height of oak trees in a park.
B)Heights and weights of newborn babies.
C)Time of a flight between Chicago and New York.
D)The number of customer arrivals to a bank between 10 am and 11 am.
A)Height of oak trees in a park.
B)Heights and weights of newborn babies.
C)Time of a flight between Chicago and New York.
D)The number of customer arrivals to a bank between 10 am and 11 am.

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
9
Just as in the case of the continuous uniform distribution,the probability density function of the normal distribution may be easily used to compute probabilities.

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
10
The letter Z is used to denote a random variable with any normal distribution.

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
11
The mean and standard deviation of the continuous uniform distribution are equal.

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
12
The probability density function of a continuous random variable can be regarded as a counterpart of the probability mass function of a discrete random variable.

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
13
The probability density function of a normal distribution is in general characterized by being symmetric and bell-shaped.

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
14
The standard normal table is also referred to as the z table.

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
15
Examples of random variables that closely follow a normal distribution include the age and the class year designation of a college student.

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
16
We are often interested in finding the probability that a continuous random variable assumes a particular value.

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
17
Which of the following is not a characteristic of a probability density function f(x)?
A)f(x)≥ 0 for all values of x.
B)f(x)is symmetric around the mean.
C)The area under f(x)over all values of x equals one.
D)f(x)becomes zero or approaches zero if x increases to +infinity or decreases to -infinity.
A)f(x)≥ 0 for all values of x.
B)f(x)is symmetric around the mean.
C)The area under f(x)over all values of x equals one.
D)f(x)becomes zero or approaches zero if x increases to +infinity or decreases to -infinity.

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
18
Cumulative distribution functions can only be used to compute probabilities for continuous random variables.

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
19
The cumulative distribution function is denoted and defined as which of the following?
A)f(x)and f(x)= P(X ≤ x)
B)f(x)and f(x)= P(X ≥ x)
C)F(x)and F(x)= P(X ≤ x)
D)F(x)and F(x)= P(X ≥ x)
A)f(x)and f(x)= P(X ≤ x)
B)f(x)and f(x)= P(X ≥ x)
C)F(x)and F(x)= P(X ≤ x)
D)F(x)and F(x)= P(X ≥ x)

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
20
Given that the probability distribution is normal,it is completely described by its mean μ > 0 and its standard deviation σ > 0.

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
21
Let X be normally distributed with mean μ and standard deviation σ > 0.Which of the following is true about the z value corresponding to a given x value?
A)A positive z = (x - μ)/σ indicates how many standard deviations x is above μ.
B)A negative z = (x - μ)/σ indicates how many standard deviations x is below μ.
C)The z value corresponding to x = μ is zero.
D)All of the above.
A)A positive z = (x - μ)/σ indicates how many standard deviations x is above μ.
B)A negative z = (x - μ)/σ indicates how many standard deviations x is below μ.
C)The z value corresponding to x = μ is zero.
D)All of the above.

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
22
The probability P(Z > 1.28)is closest to ____.
A)-0.10
B)0.10
C)0.20
D)0.90
A)-0.10
B)0.10
C)0.20
D)0.90

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
23
Suppose the average price of gasoline for a city in the United States follows a continuous uniform distribution with a lower bound of $3.50 per gallon and an upper bound of $3.80 per gallon.What is the probability a randomly chosen gas station charges more than $3.70 per gallon?
A)0.3000
B)0.3333
C)0.6667
D)1.0000
A)0.3000
B)0.3333
C)0.6667
D)1.0000

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
24
It is known that the length of a certain product X is normally distributed with μ = 20 inches and σ = 4 inches.How is the probability 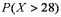 related to
related to 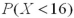 ?
?
A)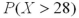 is greater than
is greater than 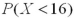 .
.
B)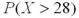 is smaller than
is smaller than 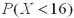 .
.
C)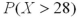 is the same as
is the same as 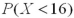 .
.
D)No comparison can be made with the given information.
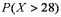 related to
related to 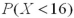 ?
?A)
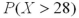 is greater than
is greater than 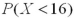 .
.B)
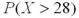 is smaller than
is smaller than 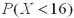 .
.C)
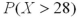 is the same as
is the same as 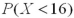 .
.D)No comparison can be made with the given information.

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
25
The waiting time at an elevator is uniformly distributed between 30 and 200 seconds.Find the mean and standard deviation of the waiting time.
A)115 seconds and 49.07 seconds
B)1.15 minutes and 0.4907 minutes
C)1.15 minutes and 24.08333 (minute)2
D)115 seconds and 2408.3333 (second)2
A)115 seconds and 49.07 seconds
B)1.15 minutes and 0.4907 minutes
C)1.15 minutes and 24.08333 (minute)2
D)115 seconds and 2408.3333 (second)2

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
26
The probability that a normal random variable is less than its mean is ___.
A)0.0
B)0.5
C)1.0
D)Cannot be determined
A)0.0
B)0.5
C)1.0
D)Cannot be determined

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
27
It is known that the length of a certain product X is normally distributed with μ = 20 inches.How is the probability 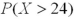 related to
related to 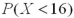 ?
?
A)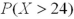 is greater than
is greater than 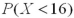 .
.
B)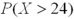 is smaller than
is smaller than 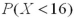 .
.
C)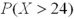 is the same as
is the same as 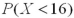 .
.
D)No comparison can be made with the given information.
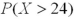 related to
related to 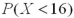 ?
?A)
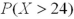 is greater than
is greater than 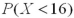 .
.B)
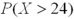 is smaller than
is smaller than 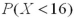 .
.C)
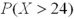 is the same as
is the same as 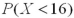 .
.D)No comparison can be made with the given information.

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
28
A continuous random variable has the uniform distribution on the interval [a,b] if its probability density function f(x)__________.
A)Is symmetric around its mean
B)Is bell-shaped between a and b
C)Is constant for all x between a and b,and 0 otherwise
D)Asymptotically approaches the x axis when x increases to +∞ or decreases to -∞
A)Is symmetric around its mean
B)Is bell-shaped between a and b
C)Is constant for all x between a and b,and 0 otherwise
D)Asymptotically approaches the x axis when x increases to +∞ or decreases to -∞

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
29
The probability P(Z < -1.28)is closest to ____.
A)-0.10
B)0.10
C)0.20
D)0.90
A)-0.10
B)0.10
C)0.20
D)0.90

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
30
The time of a call to a technical support line is uniformly distributed between 2 and 10 minutes.What are the mean and variance of this distribution?
A)6 minutes and 2.3094 (minutes)2
B)6 minutes and 5.3333 (minutes)2
C)6 minutes and 5.3333 minutes
D)8 minutes and 2.3094 minutes
A)6 minutes and 2.3094 (minutes)2
B)6 minutes and 5.3333 (minutes)2
C)6 minutes and 5.3333 minutes
D)8 minutes and 2.3094 minutes

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
31
It is known that the length of a certain product X is normally distributed with μ = 20 inches.How is the probability 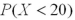 related to
related to 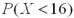 ?
?
A)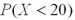 is greater than
is greater than 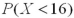 .
.
B)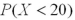 is smaller than
is smaller than 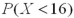 .
.
C)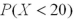 is the same as
is the same as 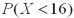 .
.
D)No comparison can be made with the given information.
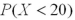 related to
related to 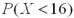 ?
?A)
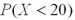 is greater than
is greater than 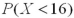 .
.B)
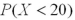 is smaller than
is smaller than 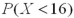 .
.C)
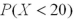 is the same as
is the same as 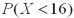 .
.D)No comparison can be made with the given information.

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
32
The height of the probability density function f(x)of the uniform distribution defined on the interval [a,b] is ____________.
A)1/(b - a)between a and b,and zero otherwise
B)(b - a)/2 between a and b,and zero otherwise
C)(a + b)/2 between a and b,and zero otherwise
D)1/(a + b)between a and b,and zero otherwise
A)1/(b - a)between a and b,and zero otherwise
B)(b - a)/2 between a and b,and zero otherwise
C)(a + b)/2 between a and b,and zero otherwise
D)1/(a + b)between a and b,and zero otherwise

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
33
The waiting time at an elevator is uniformly distributed between 30 and 200 seconds.What is the probability a rider must wait between 1 minute and 1.5 minutes?
A)0.1765
B)0.3529
C)0.5294
D)0.8824
A)0.1765
B)0.3529
C)0.5294
D)0.8824

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
34
What does it mean when we say that the tails of the normal curve are asymptotic to the x axis?
A)The tails get closer and closer to the x axis but never touch it.
B)The tails gets closer and closer to the x axis and eventually touch it.
C)The tails get closer and closer to the x axis and eventually cross this axis.
D)The tails get closer and closer to the x axis and eventually become this axis.
A)The tails get closer and closer to the x axis but never touch it.
B)The tails gets closer and closer to the x axis and eventually touch it.
C)The tails get closer and closer to the x axis and eventually cross this axis.
D)The tails get closer and closer to the x axis and eventually become this axis.

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
35
An analyst is forecasting net income for Excellence Corporation for the next fiscal year.Her low-end estimate of net income is $250,000,and her high-end estimate is $350,000.Prior research allows her to assume that net income follows a continuous uniform distribution.The probability that net income will be greater than or equal to $337,500 is _______.
A)12.5%
B)29.6%
C)87.5%
D)96.4%
A)12.5%
B)29.6%
C)87.5%
D)96.4%

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
36
It is known that the length of a certain product X is normally distributed with μ = 20 inches.How is the probability 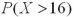 related to
related to 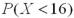 ?
?
A)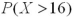 is greater than
is greater than 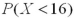 .
.
B)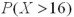 is smaller than
is smaller than 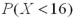 .
.
C)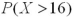 is the same as
is the same as 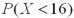 .
.
D)No comparison can be made with the given information.
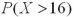 related to
related to 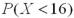 ?
?A)
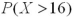 is greater than
is greater than 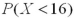 .
.B)
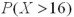 is smaller than
is smaller than 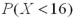 .
.C)
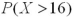 is the same as
is the same as 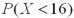 .
.D)No comparison can be made with the given information.

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
37
The waiting time at an elevator is uniformly distributed between 30 and 200 seconds.What is the probability a rider waits less than two minutes?
A)0.4706
B)0.5294
C)0.6000
D)0.7059
A)0.4706
B)0.5294
C)0.6000
D)0.7059

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
38
The waiting time at an elevator is uniformly distributed between 30 and 200 seconds.What is the probability a rider must wait more than 1.5 minutes?
A)0.3529
B)0.4500
C)0.5294
D)0.6471
A)0.3529
B)0.4500
C)0.5294
D)0.6471

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
39
How many parameters are needed to fully describe any normal distribution?
A)1
B)2
C)3
D)4
A)1
B)2
C)3
D)4

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
40
Alex is in a hurry to get to work and is rushing to catch the bus.She knows that the bus arrives every six minutes during rush hour,but does not know the exact times the bus is due.She realizes that from the time she arrives at the stop,the amount of time that she will have to wait follows a uniform distribution with a lower bound of 0 minutes and an upper bound of six minutes.What is the probability that she will have to wait more than two minutes?
A)0.1667
B)0.3333
C)0.6667
D)1.0000
A)0.1667
B)0.3333
C)0.6667
D)1.0000

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
41
A hedge fund returns on average 26% per year with a standard deviation of 12%.Using the empirical rule,approximate the probability the fund returns over 50% next year.
A)0.5%
B)1%
C)2.5%
D)5%
A)0.5%
B)1%
C)2.5%
D)5%

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
42
Let X be normally distributed with mean µ = 250 and standard deviation σ = 80.Find the value x such that P(X ≤ x)= 0.9394.
A)-1.55
B)1.55
C)126
D)374
A)-1.55
B)1.55
C)126
D)374

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
43
Let X be normally distributed with mean µ = 250 and standard deviation σ = 80.Find the value x -such that P(X ≤ x)= 0.0606.
A)-1.55
B)1.55
C)126
D)374
A)-1.55
B)1.55
C)126
D)374

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
44
Find the z value such that 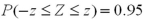 .
.
A)z = -1.645
B)z = -1.96
C)z = 1.645
D)z = 1.96
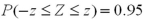 .
.A)z = -1.645
B)z = -1.96
C)z = 1.645
D)z = 1.96

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
45
Find the z value such that 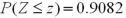 .
.
A)z = -1.33
B)z = 0.1814
C)z = 0.8186
D)z = 1.33
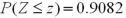 .
.A)z = -1.33
B)z = 0.1814
C)z = 0.8186
D)z = 1.33

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
46
The time to complete the construction of a soapbox derby car is normally distributed with a mean of three hours and a standard deviation of one hour.Find the probability that it would take between 2.5 and 3.5 hours to construct a soapbox derby car.
A)0.3085
B)0.3830
C)0.6170
D)0.6915
A)0.3085
B)0.3830
C)0.6170
D)0.6915

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
47
Find the probability P(-1.96 ≤ Z ≤ 1.96).
A)0.0500
B)0.9500
C)0.9750
D)1.9500
A)0.0500
B)0.9500
C)0.9750
D)1.9500

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
48
The time to complete the construction of a soapbox derby car is normally distributed with a mean of three hours and a standard deviation of one hour.Find the probability that it would take exactly 3.7 hours to construct a soapbox derby car.
A)0.0000
B)0.5000
C)0.7580
D)0.2420
A)0.0000
B)0.5000
C)0.7580
D)0.2420

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
49
The starting salary of an administrative assistant is normally distributed with a mean of $50,000 and a standard deviation of $2,500.We know that the probability of a randomly selected administrative assistant making a salary between μ - x and μ + x is 0.7416.Find the salary range referred to in this statement.
A)$42,825 to $52,825
B)$42,825 to $57,175
C)$47,175 to $52,825
D)$47,175 to $57,175
A)$42,825 to $52,825
B)$42,825 to $57,175
C)$47,175 to $52,825
D)$47,175 to $57,175

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
50
You work in marketing for a company that produces work boots.Quality control has sent you a memo detailing the length of time before the boots wear out under heavy use.They find that the boots wear out in an average of 208 days,but the exact amount of time varies,following a normal distribution with a standard deviation of 14 days.For an upcoming ad campaign,you need to know the percent of the pairs that last longer than six months-that is,180 days.Use the empirical rule to approximate this percent.
A)2.5%
B)5%
C)95%
D)97.5%
A)2.5%
B)5%
C)95%
D)97.5%

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
51
Sarah's portfolio has an expected annual return at 8%,with an annual standard deviation at 12%.If her investment returns are normally distributed,then in any given year Sarah has approximately ______________________.
A)A 50% chance that the actual return will be greater than 8%
B)About a 68% chance that the actual return will fall within 4% and 20%
C)About a 68% chance that the actual return will fall within -20% and 20%
D)About a 95% chance that the actual return will fall within -4% and 28%.
A)A 50% chance that the actual return will be greater than 8%
B)About a 68% chance that the actual return will fall within 4% and 20%
C)About a 68% chance that the actual return will fall within -20% and 20%
D)About a 95% chance that the actual return will fall within -4% and 28%.

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
52
Find the probability P(-1.96 ≤ Z ≤ 0).
A)0.0250
B)0.0500
C)0.4750
D)0.5250
A)0.0250
B)0.0500
C)0.4750
D)0.5250

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
53
The time to complete the construction of a soapbox derby car is normally distributed with a mean of three hours and a standard deviation of one hour.Find the probability that it would take more than five hours to construct a soapbox derby car.
A)0
B)0.0228
C)0.4772
D)0.9772
A)0
B)0.0228
C)0.4772
D)0.9772

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
54
The stock price of a particular asset has a mean and standard deviation of $58.50 and $8.25,respectively.Use the normal distribution to compute the 95th percentile of this stock price.
A)-1.645
B)1.645
C)44.93
D)72.07
A)-1.645
B)1.645
C)44.93
D)72.07

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
55
The salary of teachers in a particular school district is normally distributed with a mean of $50,000 and a standard deviation of $2,500.Due to budget limitations,it has been decided that the teachers who are in the top 2.5% of the salaries would not get a raise.What is the salary level that divides the teachers into one group that gets a raise and one that doesn't?
A)-1.96
B)1.96
C)45,100
D)54,900
A)-1.96
B)1.96
C)45,100
D)54,900

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
56
For any normally distributed random variable with mean μ and standard deviation σ,the percent of the observations that fall between 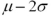 and
and 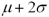 is closest to ______.
is closest to ______.
A)68%
B)68.26%
C)95%
D)95.44%
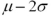 and
and 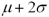 is closest to ______.
is closest to ______.A)68%
B)68.26%
C)95%
D)95.44%

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
57
For any normally distributed random variable with mean μ and standard deviation σ,the proportion of the observations that fall outside the interval [μ - σ,μ + σ] is closest to _____.
A)0.0466
B)0.3174
C)0.8413
D)0.1687
A)0.0466
B)0.3174
C)0.8413
D)0.1687

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
58
Let X be normally distributed with mean µ = 25 and standard deviation σ = 5.Find the value x such that P(X ≥ x)= 0.1736.
A)-0.94
B)0.94
C)20.30
D)29.70
A)-0.94
B)0.94
C)20.30
D)29.70

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
59
If X has a normal distribution with 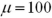 and
and 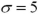 ,then the probability
,then the probability 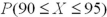 can be expressed in terms of a standard normal variable Z as _______.
can be expressed in terms of a standard normal variable Z as _______.
A)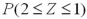
B)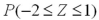
C)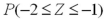
D)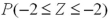
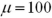 and
and 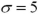 ,then the probability
,then the probability 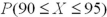 can be expressed in terms of a standard normal variable Z as _______.
can be expressed in terms of a standard normal variable Z as _______.A)
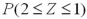
B)
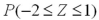
C)
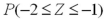
D)
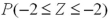

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
60
An investment consultant tells her client that the probability of making a positive return with her suggested portfolio is 0.90.What is the risk,measured by standard deviation,that this investment manager has assumed in his calculation if it is known that returns from her suggested portfolio are normally distributed with a mean of 6%?
A)1.28%
B)4.69%
C)6.00%
D)10.0%
A)1.28%
B)4.69%
C)6.00%
D)10.0%

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
61
Exhibit 6-2.Gold miners in Alaska have found,on average,12 ounces of gold per 1000 tons of dirt excavated with a standard deviation of 3 ounces.Assume the amount of gold found per 1000 tons of dirt is normally distributed. Refer to Exhibit 6-2.What is the probability the miners find more than 16 ounces of gold in the next 1000 tons of dirt excavated?
A)0.0918
B)0.4082
C)0.5918
D)0.9082
A)0.0918
B)0.4082
C)0.5918
D)0.9082

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
62
Exhibit 6-1.You are planning a May camping trip to Denali National Park in Alaska and want to make sure your sleeping bag is warm enough.The average low temperature in the park for May follows a normal distribution with a mean of 32°F and a standard deviation of 8°F. Refer to Exhibit 6-1.Above what temperature must the sleeping bag be suited such that the temperature will be too cold only 5% of the time?
A)-1.645
B)1.645
C)18.84
D)45.16
A)-1.645
B)1.645
C)18.84
D)45.16

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
63
Suppose the life of a particular brand of laptop battery is normally distributed with a mean of 8 hours and a standard deviation of 0.6 hours.What is the probability that the battery will last more than 9 hours before running out of power?
A)0.0475
B)0.4525
C)0.9525
D)1.6667
A)0.0475
B)0.4525
C)0.9525
D)1.6667

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
64
Exhibit 6-3.Patients scheduled to see their primary care physician at a particular hospital wait,on average,an additional eight minutes after their appointment is scheduled to start.Assume the time that patients wait is exponentially distributed. Refer to Exhibit 6-3.What is the probability a randomly selected patient will see the doctor within five minutes of the scheduled time?
A)0.2019
B)0.4647
C)0.5353
D)0.7981
A)0.2019
B)0.4647
C)0.5353
D)0.7981

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
65
Find the mean of the lognormal variable if the mean and standard deviation of the underlying normal variable are 2 and 0.8,respectively.
A)0.69
B)2.32
C)10.18
D)11.02
A)0.69
B)2.32
C)10.18
D)11.02

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
66
If an exponential distribution has the rate parameter λ = 5,what is its expected value?
A)5
B)1/5
C)1/25
D)5/2
A)5
B)1/5
C)1/25
D)5/2

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
67
If 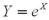 has a lognormal distribution,what can be said of the distribution of the random variable X?
has a lognormal distribution,what can be said of the distribution of the random variable X?
A)X follows a normal distribution.
B)X follows an exponential distribution.
C)X follows a standard normal distribution.
D)X follows a continuous uniform distribution.
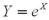 has a lognormal distribution,what can be said of the distribution of the random variable X?
has a lognormal distribution,what can be said of the distribution of the random variable X?A)X follows a normal distribution.
B)X follows an exponential distribution.
C)X follows a standard normal distribution.
D)X follows a continuous uniform distribution.

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
68
If an exponential distribution has the rate parameter λ = 5,what is its variance?
A)5
B)1/5
C)1/25
D)5/2
A)5
B)1/5
C)1/25
D)5/2

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
69
Exhibit 6-4.The average time between trades for a high-frequency trading investment firm is 40 seconds.Assume the time between trades is exponentially distributed. Refer to Exhibit 6-4.What is the probability that the time between trades for a randomly selected trade and the one proceeding it is less than 20 seconds?
A)0.1354
B)0.3935
C)0.6065
D)0.8446
A)0.1354
B)0.3935
C)0.6065
D)0.8446

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
70
Let the time between two consecutive arrivals at a grocery store check-out line be exponentially distributed with a mean of three minutes.Find the probability that the next arrival does not occur until at least four minutes have passed since the last arrival.
A)0.0000
B)0.2636
C)0.4724
D)0.7364
A)0.0000
B)0.2636
C)0.4724
D)0.7364

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
71
Exhibit 6-2.Gold miners in Alaska have found,on average,12 ounces of gold per 1000 tons of dirt excavated with a standard deviation of 3 ounces.Assume the amount of gold found per 1000 tons of dirt is normally distributed. Refer to Exhibit 6-2.What is the probability the miners find between 10 and 14 ounces of gold in the next 1000 tons of dirt excavated?
A)0.2514
B)0.4972
C)0.5028
D)0.7486
A)0.2514
B)0.4972
C)0.5028
D)0.7486

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
72
Exhibit 6-3.Patients scheduled to see their primary care physician at a particular hospital wait,on average,an additional eight minutes after their appointment is scheduled to start.Assume the time that patients wait is exponentially distributed. Refer to Exhibit 6-3.What is the probability a randomly selected patient will have to wait more than 10 minutes?
A)0.2865
B)0.4493
C)0.5507
D)0.7135
A)0.2865
B)0.4493
C)0.5507
D)0.7135

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
73
Exhibit 6-4.The average time between trades for a high-frequency trading investment firm is 40 seconds.Assume the time between trades is exponentially distributed. Refer to Exhibit 6-4.What is the probability that the time between trades for a randomly selected trade and the one proceeding it is more than a minute?
A)0.2231
B)0.4869
C)0.5134
D)0.7769
A)0.2231
B)0.4869
C)0.5134
D)0.7769

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
74
Find the variance of the lognormal variable if the mean and variance of the underlying normal variable are 2 and 1,respectively.
A)0
B)12.18
C)15.97
D)255.02
A)0
B)12.18
C)15.97
D)255.02

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
75
Exhibit 6-5.The mean travel time to work is 25.2 minutes (U.S.Census 2010).Further,suppose that commute time follows a log-normal distribution with a standard deviation of 10 minutes. Refer to Exhibit 6-5.What is the probability a randomly selected U.S.worker has a commute time of more than half an hour?
A)25.78%
B)31.56%
C)68.44%
D)74.22%
A)25.78%
B)31.56%
C)68.44%
D)74.22%

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
76
Exhibit 6-1.You are planning a May camping trip to Denali National Park in Alaska and want to make sure your sleeping bag is warm enough.The average low temperature in the park for May follows a normal distribution with a mean of 32°F and a standard deviation of 8°F. Refer to Exhibit 6-1.An inexpensive bag you are considering advertises to be good for temperatures down to 38°F.What is the probability that the bag will not be warm enough?
A)0.2266
B)0.2734
C)0.7500
D)0.7734
A)0.2266
B)0.2734
C)0.7500
D)0.7734

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
77
Exhibit 6-2.Gold miners in Alaska have found,on average,12 ounces of gold per 1000 tons of dirt excavated with a standard deviation of 3 ounces.Assume the amount of gold found per 1000 tons of dirt is normally distributed. Refer to Exhibit 6-2.If the miners excavated 1000 tons of dirt,how little gold must they have found such that they find that amount or less only 15% of the time?
A)-1.04
B)1.04
C)8.88
D)15.12
A)-1.04
B)1.04
C)8.88
D)15.12

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
78
Exhibit 6-5.The mean travel time to work is 25.2 minutes (U.S.Census 2010).Further,suppose that commute time follows a log-normal distribution with a standard deviation of 10 minutes. Refer to Exhibit 6-5.What is the probability a randomly selected U.S.worker has a commute time of less than 20 minutes?
A)30.15%
B)34.09%
C)65.91%
D)69.85%
A)30.15%
B)34.09%
C)65.91%
D)69.85%

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
79
What can be said about the expected value and standard deviation of an exponential distribution?
A)The expected value is equal to the standard deviation.
B)The expected value is equal to the square of the standard deviation.
C)The expected value is equal to the reciprocal of the standard deviation.
D)The expected value is equal to the square root of the standard deviation.
A)The expected value is equal to the standard deviation.
B)The expected value is equal to the square of the standard deviation.
C)The expected value is equal to the reciprocal of the standard deviation.
D)The expected value is equal to the square root of the standard deviation.

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
80
Exhibit 6-1.You are planning a May camping trip to Denali National Park in Alaska and want to make sure your sleeping bag is warm enough.The average low temperature in the park for May follows a normal distribution with a mean of 32°F and a standard deviation of 8°F. Refer to Exhibit 6-1.One sleeping bag you are considering advertises that it is good for temperatures down to 25°F.What is the probability that this bag will be warm enough on a randomly selected May night at the park?
A)0.1894
B)0.3106
C)0.8106
D)0.8800
A)0.1894
B)0.3106
C)0.8106
D)0.8800

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck


