Deck 2: An Introduction to Linear Programming
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/56
Play
Full screen (f)
Deck 2: An Introduction to Linear Programming
1
An unbounded feasible region might not result in an unbounded solution for a minimization or maximization problem.
True
2
For a minimization problem,the solution is considered to be unbounded if the value may be made infinitely small.
True
3
The constraint 5x1 − 2x2 ≤ 0 passes through the point (20,50).
True
4
A linear programming problem can be both unbounded and infeasible.

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
5
If a constraint is redundant,it can be removed from the problem without affecting the feasible region.

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
6
The optimal solution to any linear programming problem is the same as the optimal solution to the standard form of the problem.

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
7
It is not possible to have more than one optimal solution to a linear programming problem.

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
8
Constraints limit the degree to which the objective in a linear programming problem is satisfied.

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
9
An optimal solution to a linear programming problem can be found at an extreme point of the feasible region for the problem.

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
10
At a problem's optimal solution,a redundant constraint will have zero slack.

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
11
A redundant constraint cannot be removed from the problem without affecting the feasible region.

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
12
The constraint 2x1 − x2 = 0 passes through the point (200,100).

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
13
Because surplus variables represent the amount by which the solution exceeds a minimum target,they are given positive coefficients in the objective function.

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
14
In a linear programming problem,the objective function and the constraints must be linear functions of the decision variables.

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
15
The maximization or minimization of a desired quantity is the
A)goal of management science.
B)decision for decision analysis.
C)constraint of operations research.
D)objective of linear programming.
A)goal of management science.
B)decision for decision analysis.
C)constraint of operations research.
D)objective of linear programming.

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
16
Only binding constraints form the shape (boundaries)of the feasible region.

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
17
An infeasible problem is one in which the objective function can be increased to infinity.

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
18
Alternative optimal solutions occur when there is no feasible solution to the problem.

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
19
No matter what value it has,each objective function line is parallel to every other objective function line in a problem.

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
20
The point (3,2)is feasible for the constraint 2x1 + 6x2 ≤ 30.

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
21
In which part(s)of a linear programming formulation would the decision variables be stated?
A)objective function and the left-hand side of each constraint
B)objective function and the right-hand side of each constraint
C)the left-hand side of each constraint only
D)the objective function only
A)objective function and the left-hand side of each constraint
B)objective function and the right-hand side of each constraint
C)the left-hand side of each constraint only
D)the objective function only

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
22
When no solution to the linear programming problem satisfies all the constraints,including the nonnegativity conditions,it is considered
A)optimal.
B)feasible.
C)infeasible.
D)semifeasible.
A)optimal.
B)feasible.
C)infeasible.
D)semifeasible.

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
23
If there is a maximum of 4,000 hours of labor available per month and 300 ping-pong balls (x1)or 125 wiffle balls (x2)can be produced per hour of labor,which of the following constraints reflects this situation?
A)300x1 + 125x2 > 4,000
B)300x1 + 125x2 < 4,000
C)425(x1 + x2)< 4,000
D)300x1 + 125x2 = 4,000
A)300x1 + 125x2 > 4,000
B)300x1 + 125x2 < 4,000
C)425(x1 + x2)< 4,000
D)300x1 + 125x2 = 4,000

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
24
Which of the following special cases does NOT require reformulation of the problem in order to obtain a solution?
A)alternative optimality
B)infeasibility
C)unboundedness
D)Each case requires a reformulation.
A)alternative optimality
B)infeasibility
C)unboundedness
D)Each case requires a reformulation.

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
25
Solve the following system of simultaneous equations.6X + 2Y = 50
2X + 4Y = 20
2X + 4Y = 20

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
26
The amount by which the left side of a less-than-or-equal-to constraint is smaller than the right side
A)is known as a surplus.
B)is known as slack.
C)is optimized for the linear programming problem.
D)exists for each variable in a linear programming problem.
A)is known as a surplus.
B)is known as slack.
C)is optimized for the linear programming problem.
D)exists for each variable in a linear programming problem.

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
27
Consider the following linear programming problem: 
a.Use a graph to show each constraint and the feasible region.
b.Identify the optimal solution point on your graph.What are the values of X and Y at the optimal solution?
c.What is the optimal value of the objective function?

a.Use a graph to show each constraint and the feasible region.
b.Identify the optimal solution point on your graph.What are the values of X and Y at the optimal solution?
c.What is the optimal value of the objective function?

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
28
A redundant constraint results in
A)no change in the optimal solution(s).
B)an unbounded solution.
C)no feasible solution.
D)alternative optimal solutions.
A)no change in the optimal solution(s).
B)an unbounded solution.
C)no feasible solution.
D)alternative optimal solutions.

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
29
All of the following statements about a redundant constraint are correct EXCEPT
A)a redundant constraint does not affect the optimal solution.
B)a redundant constraint does not affect the feasible region.
C)recognizing a redundant constraint is easy with the graphical solution method.
D)at the optimal solution,a redundant constraint will have zero slack.
A)a redundant constraint does not affect the optimal solution.
B)a redundant constraint does not affect the feasible region.
C)recognizing a redundant constraint is easy with the graphical solution method.
D)at the optimal solution,a redundant constraint will have zero slack.

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
30
Solve the following system of simultaneous equations.6X + 4Y = 40
2X + 3Y = 20
2X + 3Y = 20

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
31
The three assumptions necessary for a linear programming model to be appropriate include all of the following EXCEPT
A)proportionality.
B)additivity.
C)divisibility.
D)normality.
A)proportionality.
B)additivity.
C)divisibility.
D)normality.

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
32
Which of the following is a valid objective function for a linear programming problem?
A)Min 8xy
B)Min 4x + 3y + (1/2)z
C)Min 5x2 + 6y2
D)Max (x1 + x2)/x3
A)Min 8xy
B)Min 4x + 3y + (1/2)z
C)Min 5x2 + 6y2
D)Max (x1 + x2)/x3

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
33
For the following linear programming problem,determine the optimal solution using the graphical solution method. 


Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
34
To find the optimal solution to a linear programming problem using the graphical method,
A)find the feasible point that is the farthest away from the origin.
B)find the feasible point that is at the highest location.
C)find the feasible point that is closest to the origin.
D)None of these are correct.
A)find the feasible point that is the farthest away from the origin.
B)find the feasible point that is at the highest location.
C)find the feasible point that is closest to the origin.
D)None of these are correct.

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
35
A constraint that does NOT affect the feasible region of the solution is a
A)nonnegativity constraint.
B)redundant constraint.
C)standard constraint.
D)slack constraint.
A)nonnegativity constraint.
B)redundant constraint.
C)standard constraint.
D)slack constraint.

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
36
A variable added to the left-hand side of a less-than-or-equal-to constraint to convert the constraint into an equality is a
A)standard variable.
B)slack variable.
C)surplus variable.
D)nonnegative variable.
A)standard variable.
B)slack variable.
C)surplus variable.
D)nonnegative variable.

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
37
Decision variables
A)are values that are used to determine how much or how many of something to produce,invest,etc.
B)represent the values of the constraints.
C)are values that measure the objective function.
D)must be unique for each constraint.
A)are values that are used to determine how much or how many of something to produce,invest,etc.
B)represent the values of the constraints.
C)are values that measure the objective function.
D)must be unique for each constraint.

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
38
All linear programming problems have all of the following properties EXCEPT
A)a linear objective function that is to be maximized or minimized.
B)a set of linear constraints.
C)alternative optimal solutions.
D)variables that are all restricted to nonnegative values.
A)a linear objective function that is to be maximized or minimized.
B)a set of linear constraints.
C)alternative optimal solutions.
D)variables that are all restricted to nonnegative values.

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
39
Whenever all the constraints in a linear program are expressed as equalities,the linear program is said to be written in
A)standard form.
B)bounded form.
C)feasible form.
D)alternative form.
A)standard form.
B)bounded form.
C)feasible form.
D)alternative form.

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
40
Which of the following statements is NOT true?
A)A feasible solution satisfies all constraints.
B)An optimal solution satisfies all constraints.
C)An infeasible solution violates all constraints.
D)A feasible solution point does not have to lie on the boundary of the feasible region.
A)A feasible solution satisfies all constraints.
B)An optimal solution satisfies all constraints.
C)An infeasible solution violates all constraints.
D)A feasible solution point does not have to lie on the boundary of the feasible region.

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
41
Consider the following linear program: 
a.Write the problem in standard form.
b.What is the feasible region for the problem?
c.Show that regardless of the values of the actual objective function coefficients,the optimal solution will occur at one of two points.Solve for these points and then determine which one maximizes the current objective function.

a.Write the problem in standard form.
b.What is the feasible region for the problem?
c.Show that regardless of the values of the actual objective function coefficients,the optimal solution will occur at one of two points.Solve for these points and then determine which one maximizes the current objective function.

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
42
Does the following linear programming problem exhibit infeasibility,unboundedness,or alternative optimal solutions? Explain. 


Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
43
Muir Manufacturing produces two popular grades of commercial carpeting among its many other products.In the coming production period,Muir needs to decide how many rolls of each grade should be produced in order to maximize profit.Each roll of Grade X carpet uses 50 units of synthetic fiber,requires 25 hours of production time,and needs 20 units of foam backing.Each roll of Grade Y carpet uses 40 units of synthetic fiber,requires 28 hours of production time,and needs 15 units of foam backing.
The profit per roll of Grade X carpet is $200,and the profit per roll of Grade Y carpet is $160.In the coming production period,Muir has 3000 units of synthetic fiber available for use.Workers have been scheduled to provide at least 1800 hours of production time (overtime is a possibility).The company has 1500 units of foam backing available for use.
Develop and solve a linear programming model for this problem.
The profit per roll of Grade X carpet is $200,and the profit per roll of Grade Y carpet is $160.In the coming production period,Muir has 3000 units of synthetic fiber available for use.Workers have been scheduled to provide at least 1800 hours of production time (overtime is a possibility).The company has 1500 units of foam backing available for use.
Develop and solve a linear programming model for this problem.

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
44
Solve the following linear program graphically.How many extreme points exist for this problem?



Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
45
The Sanders Garden Shop mixes two types of grass seed into a blend.Each type of grass has been rated (per pound)according to its shade tolerance,ability to stand up to traffic,and drought resistance,as shown in the table.Type A seed costs $1 and Type B seed costs $2. 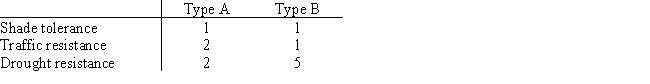
a.If the blend needs to score at least 300 points for shade tolerance,400 points for traffic resistance,and 750 points for drought resistance,how many pounds of each seed should be in the blend?
b.Which targets will be exceeded?
c.How much will the blend cost?
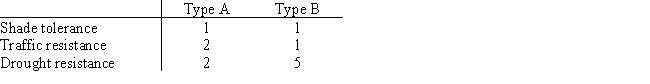
a.If the blend needs to score at least 300 points for shade tolerance,400 points for traffic resistance,and 750 points for drought resistance,how many pounds of each seed should be in the blend?
b.Which targets will be exceeded?
c.How much will the blend cost?

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
46
Solve the following linear program graphically. 


Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
47
A businessman is considering opening a small specialized trucking firm.To make the firm profitable,it must have a daily trucking capacity of at least 84,000 cubic feet.Two types of trucks are appropriate for the specialized operation.Their characteristics and costs are summarized in the table below.Note that truck two requires three drivers for long haul trips.There are 41 potential drivers available,and there are facilities for at most 40 trucks.The businessman's objective is to minimize the total cost outlay for trucks. 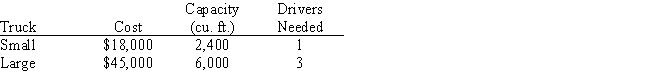
Solve the problem graphically and note that there are alternative optimal solutions.
a.Which optimal solution uses only one type of truck?
b.Which optimal solution utilizes the minimum total number of trucks?
c.Which optimal solution uses the same number of small and large trucks?
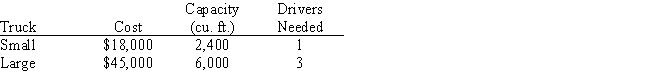
Solve the problem graphically and note that there are alternative optimal solutions.
a.Which optimal solution uses only one type of truck?
b.Which optimal solution utilizes the minimum total number of trucks?
c.Which optimal solution uses the same number of small and large trucks?

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
48
Solve the following linear program graphically. 


Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
49
Does the following linear programming problem exhibit infeasibility,unboundedness,or alternative optimal solutions? Explain. 


Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
50
Find the complete optimal solution to this linear programming problem. 


Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
51
Maxwell Manufacturing makes two models of felt-tip marking pens.Requirements for each lot of pens are given below. 
The profit for either model is $1000 per lot.
a.What is the linear programming model for this problem?
b.Find the optimal solution.
c.Will there be excess capacity in any resource?

The profit for either model is $1000 per lot.
a.What is the linear programming model for this problem?
b.Find the optimal solution.
c.Will there be excess capacity in any resource?

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
52
For the following linear programming problem,determine the optimal solution using the graphical solution method.Are any of the constraints redundant? If yes,identify the constraint that is redundant. 


Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
53
Find the complete optimal solution to this linear programming problem. 


Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
54
Find the complete optimal solution to this linear programming problem. 


Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
55
Use this graph to answer the questions. 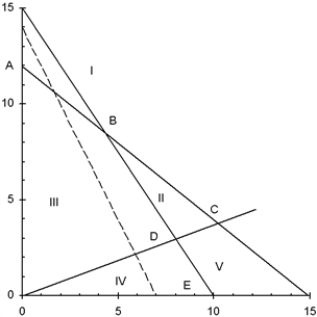

a.Which area (I,II,III,IV,or V)forms the feasible region?
b.Which point (A,B,C,D,or E)is optimal?
c.Which constraints are binding?
d.Which slack variables equal zero?


a.Which area (I,II,III,IV,or V)forms the feasible region?
b.Which point (A,B,C,D,or E)is optimal?
c.Which constraints are binding?
d.Which slack variables equal zero?

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
56
Find the complete optimal solution to this linear programming problem. 


Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck


