Deck 1: Fundamentals
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/229
Play
Full screen (f)
Deck 1: Fundamentals
1
State whether the inequality is true or false.
False
2
Perform the indicated operation.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)
3
Write the following statement in terms of inequalities. is greater than or equal to .
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)
4
Perform the indicated operation.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
5
Perform the indicated operations. 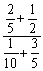
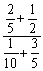

Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
6
State whether the inequality is true or false.

Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
7
Write the following statement in terms of inequalities. is negative.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
8
Use properties of real numbers to write without parentheses.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
9
Perform the indicated operations. 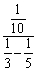
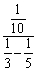

Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
10
Use the properties of real numbers to write the expression without parentheses.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
11
State the property of real numbers being used.
A) Commutative Property for addition
B) Commutative Property for multiplication
C) Associative Property for addition
D) Associative Property for multiplication
E) Distributive Property
A) Commutative Property for addition
B) Commutative Property for multiplication
C) Associative Property for addition
D) Associative Property for multiplication
E) Distributive Property

Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
12
State the property of real numbers being used.
A) Commutative Property for addition
B) Commutative Property for multiplication
C) Associative Property for addition
D) Associative Property for multiplication
E) Distributive Property
A) Commutative Property for addition
B) Commutative Property for multiplication
C) Associative Property for addition
D) Associative Property for multiplication
E) Distributive Property

Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
13
Perform the indicated operations. 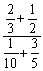
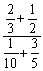

Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
14
State whether the inequality is true or false.

Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
15
Perform the indicated operations. 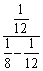
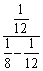

Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
16
Perform the indicated operation(s) and simplify.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
17
Use properties of real numbers to write without parentheses.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
18
Use properties of real numbers to write without parentheses.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
19
State the property of real numbers being used.
A) Commutative Property for addition
B) Commutative Property for multiplication
C) Associative Property for addition
D) Associative Property for multiplication
E) Distributive Property
A) Commutative Property for addition
B) Commutative Property for multiplication
C) Associative Property for addition
D) Associative Property for multiplication
E) Distributive Property

Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
20
Perform the indicated operation(s) and simplify.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
21
Evaluate
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
22
Evaluate the expression. 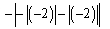
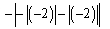

Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
23
Evaluate each expression.
(a)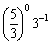
(b)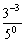
(c)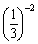
(a)
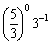
(b)
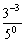
(c)
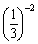

Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
24
Evaluate the expression.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
25
Evaluate the expression. 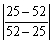
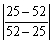

Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
26
Express the repeating decimal as a fraction. 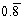
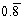

Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
27
Find the set if and
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
28
Evaluate
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
29
Write the statement in terms of inequalities. The distance from x to 3 is at most .
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
30
Express the repeating decimal 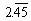 as a fraction.
as a fraction.
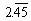 as a fraction.
as a fraction.
Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
31
Simplify and eliminate any negative exponents.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
32
Evaluate the expression. 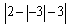
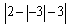

Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
33
Simplify and eliminate any negative exponents.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
34
Evaluate each expression.
(a)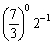
(b)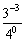
(c)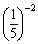
(a)
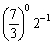
(b)
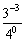
(c)
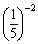

Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
35
Find the distance between 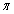 and .
and . 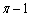
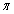 and .
and . 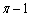

Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
36
Evaluate
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
37
Find if and .
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
38
Evaluate
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
39
Express the repeating decimal as a fraction. 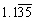
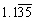

Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
40
Evaluate
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
41
Simplify the expression. Assume the letters denote any real numbers. 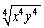
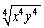

Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
42
Write the number in the statement in scientific notation. The distance to the edge of the observable universe is about 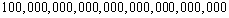 m.
m.
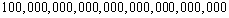 m.
m.
Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
43
Write 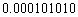 in scientific notation.
in scientific notation.
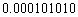 in scientific notation.
in scientific notation.
Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
44
Simplify the expression and eliminate any negative exponents(s).
Assume that all letters denote positive numbers.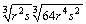
Assume that all letters denote positive numbers.
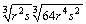

Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
45
Find the sum, difference, or product. 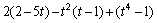
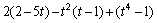

Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
46
Simplify the expression. Assume the letters denote any real numbers. 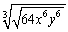
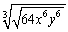

Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
47
A sealed warehouse measuring 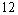 m wide,
m wide, 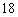 m long and 6 m high, is filled with pure oxygen. One cubic meter contains 1000 L, and 22.4 L of any gas contains
m long and 6 m high, is filled with pure oxygen. One cubic meter contains 1000 L, and 22.4 L of any gas contains 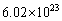 molecules. How many molecules of oxygen are there in the room?
molecules. How many molecules of oxygen are there in the room?
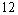 m wide,
m wide, 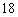 m long and 6 m high, is filled with pure oxygen. One cubic meter contains 1000 L, and 22.4 L of any gas contains
m long and 6 m high, is filled with pure oxygen. One cubic meter contains 1000 L, and 22.4 L of any gas contains 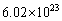 molecules. How many molecules of oxygen are there in the room?
molecules. How many molecules of oxygen are there in the room?
Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
48
Simplify the expression and eliminate any negative exponents(s).
Assume that all letters denote positive numbers.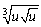
Assume that all letters denote positive numbers.
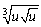

Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
49
Perform the indicated operations and simplify.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
50
Rationalize the denominator. 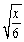
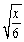

Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
51
Simplify the expression. Assume the letters denote any real numbers. 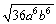
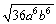

Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
52
Write the number in the statement in scientific notation:
The mass of a proton is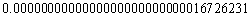 kg.
kg.
The mass of a proton is
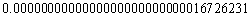 kg.
kg.
Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
53
Rationalize the denominator. 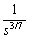
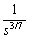

Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
54
Simplify the expression. Assume the letters denote any real numbers. 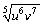
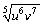

Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
55
Which of the numbers 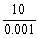 and
and 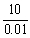 is smaller?
is smaller?
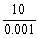 and
and 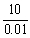 is smaller?
is smaller?
Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
56
Write 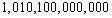 in scientific notation.
in scientific notation.
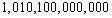 in scientific notation.
in scientific notation.
Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
57
Simplify the expression 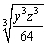 .
.
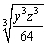 .
.
Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
58
Use scientific notation, laws of exponents, and a calculator to perform the indicated operations. State your answer correct to the number of significant digits indicated by the data. 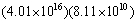
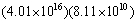

Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
59
Simplify the expression and eliminate any negative exponents(s).
Assume that all letters denote positive numbers.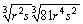
Assume that all letters denote positive numbers.
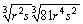

Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
60
Perform the indicated operations and simplify.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
61
Perform the indicated operations and simplify.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
62
Factor the expression.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
63
Perform the indicated operations and simplify.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
64
Perform the indicated operations and simplify.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
65
Perform the indicated operations and simplify.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
66
Factor the expression.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
67
Factor the expression.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
68
Multiply the algebraic expressions using a Special Product Formula and simplify. 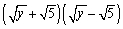
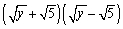

Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
69
Factor out the common factor. 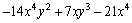
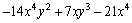

Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
70
Multiply the algebraic expressions using a Special Product Formula and simplify. 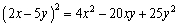
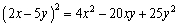

Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
71
Factor the expression.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
72
Multiply the algebraic expressions using a Special Product Formula and simplify. 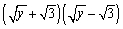
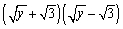

Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
73
Use a Factoring Formula to factor the expression. 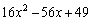
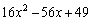

Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
74
Multiply the algebraic expressions using a Special Product Formula and simplify. 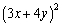
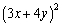

Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
75
Find the sum, difference, or product. 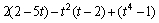
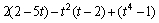

Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
76
Multiply the algebraic expressions using the FOIL method and simplify. 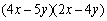
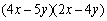

Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
77
Factor the expression.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
78
Perform the indicated operations and simplify.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
79
Factor the expression.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
80
Perform the indicated operations and simplify.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck


