Deck 16: Superposition and Standing Waves
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/125
Play
Full screen (f)
Deck 16: Superposition and Standing Waves
1
When a piano tuner strikes both the A above middle C on the piano and a 440 Hz tuning fork, he hears 4 beats each second. The frequency of the piano's A is
A) 440 Hz
B) 444 Hz
C) 880 Hz
D) 436 Hz
E) either 436 Hz or 444 Hz
A) 440 Hz
B) 444 Hz
C) 880 Hz
D) 436 Hz
E) either 436 Hz or 444 Hz
either 436 Hz or 444 Hz
2
Two wave trains of the same frequency are traveling in opposite directions down a string. When they meet, these wave trains will not
A) be described by the principle of superposition.
B) reflect from each other.
C) pass through one another.
D) continue to carry energy.
E) remain transverse.
A) be described by the principle of superposition.
B) reflect from each other.
C) pass through one another.
D) continue to carry energy.
E) remain transverse.
reflect from each other.
3
Two tones of equal amplitude but slightly different frequencies are emitted by a sound source. This gives rise to
A) standing waves.
B) destructive interference.
C) constructive interference.
D) beats.
E) amplification.
A) standing waves.
B) destructive interference.
C) constructive interference.
D) beats.
E) amplification.
beats.
4
A violinist is tuning the A string on her violin by listening for beats when this note is played simultaneously with a tuning fork of frequency 440 Hz. She hears a beat frequency of 4 Hz. She notices that, when she increases the tension in the string slightly, the beat frequency decreases. What was the frequency of the mistuned A string?
A) 448 Hz
B) 444 Hz
C) 436 Hz
D) 432 Hz
E) 438 Hz
A) 448 Hz
B) 444 Hz
C) 436 Hz
D) 432 Hz
E) 438 Hz

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
5
What is the phase difference at any given instant between two points on a wave which are 1.52 m apart if the wavelength of the wave is 2.13 m?
A) 0.430 rad
B) 2.70 rad
C) 4.48 rad
D) 44.0 rad
E) 119 rad
A) 0.430 rad
B) 2.70 rad
C) 4.48 rad
D) 44.0 rad
E) 119 rad

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
6
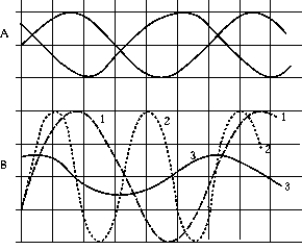 In graph A, two waves are shown at a given instant. What is the number of the curve in graph B that represents the wave resulting from the superposition of the two waves in A at this instant?
In graph A, two waves are shown at a given instant. What is the number of the curve in graph B that represents the wave resulting from the superposition of the two waves in A at this instant?A) 1
B) 2
C) 3
D) The resultant is zero for all values of x.
E) None of these represent the wave.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
7
The interference of waves refers to the
A) slowing down of one wave in the presence of another.
B) resultant disturbance of two or more waves at every point in the medium.
C) change in wavelength that occurs when two waves cross one another.
D) phase change of 180º that occurs on reflection of a wave at a fixed end.
E) ability of waves to go around corners.
A) slowing down of one wave in the presence of another.
B) resultant disturbance of two or more waves at every point in the medium.
C) change in wavelength that occurs when two waves cross one another.
D) phase change of 180º that occurs on reflection of a wave at a fixed end.
E) ability of waves to go around corners.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
8
Two waves with the same frequency and wavelength but with different amplitudes are added. If A1 = 2A2 and the waves are 180º out of phase, then the amplitude of the resultant wave is
A) zero.
B) the same as A1.
C) the same as A2.
D) equal to A1 + A2.
E) coherent.
A) zero.
B) the same as A1.
C) the same as A2.
D) equal to A1 + A2.
E) coherent.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
9
Middle C on a piano has a frequency of 262 Hz. Sometimes it is said that middle C is actually 28 = 256 Hz, and tuning forks are made with this frequency. How many beats per second would be heard if such a tuning fork were sounded simultaneously with the middle C of a (well-tuned) piano?
A) 3
B) 6
C) 12
D) 4
E) 8
A) 3
B) 6
C) 12
D) 4
E) 8

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
10
If two identical waves with the same phase are added, the result is
A) a wave with the same frequency but twice the amplitude.
B) a wave with the same amplitude but twice the frequency.
C) a wave with zero amplitude.
D) a wave with zero frequency.
E) This problem cannot be solved without knowing the wavelengths of the two waves.
A) a wave with the same frequency but twice the amplitude.
B) a wave with the same amplitude but twice the frequency.
C) a wave with zero amplitude.
D) a wave with zero frequency.
E) This problem cannot be solved without knowing the wavelengths of the two waves.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
11
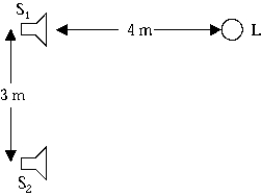 Two loudspeakers S1 and S2, 3.0 m apart, emit the same single-frequency tone in phase at the speakers. A listener L directly in front of speaker S1 notices that the intensity is a minimum when she is 4.0 m from that speaker (see figure). What is the lowest frequency of the emitted tone? The speed of sound in air is 340 m/s.
Two loudspeakers S1 and S2, 3.0 m apart, emit the same single-frequency tone in phase at the speakers. A listener L directly in front of speaker S1 notices that the intensity is a minimum when she is 4.0 m from that speaker (see figure). What is the lowest frequency of the emitted tone? The speed of sound in air is 340 m/s.A) 85 Hz
B) 0.17 kHz
C) 0.26 kHz
D) 0.34 kHz
E) 0.51 kHz

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
12
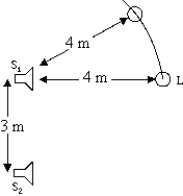 Two loudspeakers S1 and S2, 3.0 m apart, emit the same single-frequency tone in phase at the speakers. A listener directly in front of speaker S1 notices that the intensity is a minimum when she is 4.0 m from that speaker (see figure). The listener now walks around speaker S1 in an arc of a circle, staying 4.0 m from that speaker but increasing her distance from the other speaker. How far is she from speaker S2 when she notices the first maximum in the sound intensity? The speed of sound in air is 340 m/s.
Two loudspeakers S1 and S2, 3.0 m apart, emit the same single-frequency tone in phase at the speakers. A listener directly in front of speaker S1 notices that the intensity is a minimum when she is 4.0 m from that speaker (see figure). The listener now walks around speaker S1 in an arc of a circle, staying 4.0 m from that speaker but increasing her distance from the other speaker. How far is she from speaker S2 when she notices the first maximum in the sound intensity? The speed of sound in air is 340 m/s.A) 4.5 m
B) 5.0 m
C) 5.5 m
D) 6.0 m
E) 6.5 m

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
13
If two identical waves with a phase difference of 3 are added, the result is
A) a wave with the same frequency but twice the amplitude.
B) a wave with the same amplitude but twice the frequency.
C) a wave with zero amplitude.
D) a wave with an intensity equal to the sum of the intensities of the two waves.
E) This problem cannot be solved without knowing the wavelengths of the two waves.
A) a wave with the same frequency but twice the amplitude.
B) a wave with the same amplitude but twice the frequency.
C) a wave with zero amplitude.
D) a wave with an intensity equal to the sum of the intensities of the two waves.
E) This problem cannot be solved without knowing the wavelengths of the two waves.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
14
If two identical waves with a phase difference of 6 are added, the result is
A) a wave with the same frequency but twice the amplitude.
B) a wave with the same amplitude but twice the frequency.
C) a wave with zero amplitude.
D) a wave with zero frequency.
E) This problem cannot be solved without knowing the wavelengths of the two waves.
A) a wave with the same frequency but twice the amplitude.
B) a wave with the same amplitude but twice the frequency.
C) a wave with zero amplitude.
D) a wave with zero frequency.
E) This problem cannot be solved without knowing the wavelengths of the two waves.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
15
A wave on a string has a frequency of 100 Hz and travels at a speed of 24 m/s. The minimum distance between two points with a phase difference of 60º is
A) 0.040 m
B) 0.12 m
C) 0.14 m
D) 0.24 m
E) 25 m
A) 0.040 m
B) 0.12 m
C) 0.14 m
D) 0.24 m
E) 25 m

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
16
Tuning fork A has a frequency of 440 Hz. When A and a second tuning fork B are struck simultaneously, four beats per second are heard. When a small mass is added to one of the tines of B, the two forks struck simultaneously produce two beats per second. The original frequency of tuning fork B was
A) 448 Hz
B) 444 Hz
C) 438 Hz
D) 436 Hz
E) 432 Hz
A) 448 Hz
B) 444 Hz
C) 438 Hz
D) 436 Hz
E) 432 Hz

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
17
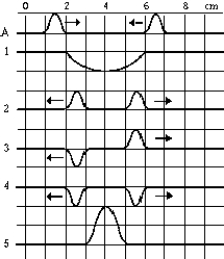 Sketch A shows two identical pulses traveling in opposite directions along a string, each with a velocity of 1.0 cm/s. After 4.0 s, the string will look like which of the other sketches?
Sketch A shows two identical pulses traveling in opposite directions along a string, each with a velocity of 1.0 cm/s. After 4.0 s, the string will look like which of the other sketches?A) 1
B) 2
C) 3
D) 4
E) 5

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
18
Two trumpet players are both playing a pitch with a frequency of 440 Hz, corresponding to the musical pitch A above middle C. However, one of the trumpet players is marching away from you so that you hear a beat frequency of 4 Hz from the two trumpets. With what speed is the departing trumpet player moving away from you? (The speed of sound in air is 340 m/s)
A) 3.12 m/s
B) 3.09 m/s
C) 3.06 m/s
D) 3.00 m/s
E) 2.95 m/s
A) 3.12 m/s
B) 3.09 m/s
C) 3.06 m/s
D) 3.00 m/s
E) 2.95 m/s

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
19
Two whistles produce sounds with wavelengths 3.40 m and 3.30 m. What is the beat frequency produced? (the speed of sound is 340 m/s)
A) 0.1 Hz
B) 1.0 Hz
C) 2.0 Hz
D) 3.0 Hz
E) 4.0 Hz
A) 0.1 Hz
B) 1.0 Hz
C) 2.0 Hz
D) 3.0 Hz
E) 4.0 Hz

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
20
The air columns in two identical pipes vibrate at frequencies of 150 Hz. The percentage of change needed in the length of one of the pipes to produce 3 beats per second is
A) 1%
B) 2%
C) 3%
D) 4%
E) 5%
A) 1%
B) 2%
C) 3%
D) 4%
E) 5%

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
21
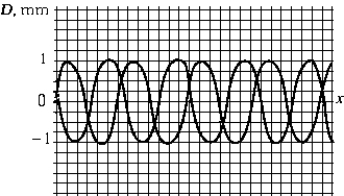 The figure shows two waves traveling in the positive-x direction. The amplitude of the resultant wave is closest to
The figure shows two waves traveling in the positive-x direction. The amplitude of the resultant wave is closest toA) 2.0 mm
B) 1.8 mm
C) 1.4 mm
D) 1.0 mm
E) zero

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
22
Two wave trains travel on a string under a constant tension T. Which of the following statements is NOT correct?
A) The two waves can have different speed.
B) The two waves can have different frequency.
C) The two waves can have different wavelength.
D) The superposition principle applies for the two waves.
E) At any point on the string, the resultant amplitude is the algebraic sum of the amplitudes of the two waves.
A) The two waves can have different speed.
B) The two waves can have different frequency.
C) The two waves can have different wavelength.
D) The superposition principle applies for the two waves.
E) At any point on the string, the resultant amplitude is the algebraic sum of the amplitudes of the two waves.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
23
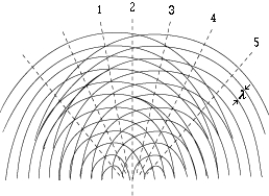 The sources S1 and S2 are coherent sources, and the circular arcs represent wave crests. The position that corresponds to a path difference of two wavelengths is
The sources S1 and S2 are coherent sources, and the circular arcs represent wave crests. The position that corresponds to a path difference of two wavelengths isA) 1
B) 2
C) 3
D) 4
E) 5

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
24
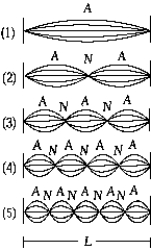 The figure represents a string of length L, fixed at both ends, vibrating in several harmonics. The 4th harmonic is shown in
The figure represents a string of length L, fixed at both ends, vibrating in several harmonics. The 4th harmonic is shown inA) 1
B) 2
C) 3
D) 4
E) 5

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
25
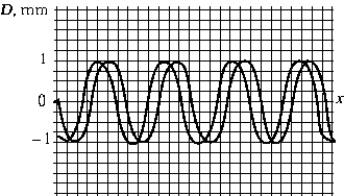 The figure shows two waves traveling in the positive-x direction. The phase difference between these two waves is closest to
The figure shows two waves traveling in the positive-x direction. The phase difference between these two waves is closest toA) 1.0 radians.
B) 1.5 radians.
C) 2.0 radians.
D) 2.5 radians.
E) 3.0 radians.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
26
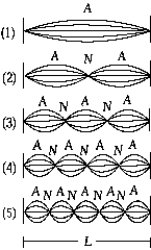 The figure represents a string of length L, fixed at both ends, vibrating in several harmonics. The 3rd harmonic is shown in
The figure represents a string of length L, fixed at both ends, vibrating in several harmonics. The 3rd harmonic is shown inA) 1
B) 2
C) 3
D) 4
E) 5

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
27
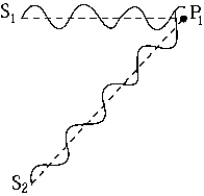 At P1, the waves from sources S1 and S2 shown in the figure
At P1, the waves from sources S1 and S2 shown in the figureA) are out of phase.
B) have a path difference of one wavelength.
C) have a path difference of two wavelengths.
D) are interfering destructively.
E) None of these is correct.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
28
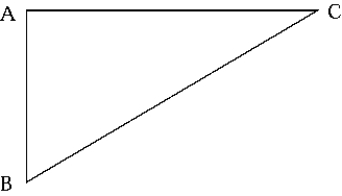 One source of sound is at A and another is at B. The two sources are in phase. The distance AB = 10.0 m. The frequency of the sound waves from both sources is 1000 Hz, and both have the same amplitude. The speed of sound in air is 330 m/s. A receiver is at point C, and AB is perpendicular to AC. The greatest distance AC for which the signal at C is a minimum is
One source of sound is at A and another is at B. The two sources are in phase. The distance AB = 10.0 m. The frequency of the sound waves from both sources is 1000 Hz, and both have the same amplitude. The speed of sound in air is 330 m/s. A receiver is at point C, and AB is perpendicular to AC. The greatest distance AC for which the signal at C is a minimum isA) 33.0 cm
B) 152 m
C) 330 m
D) 303 m
E) 100 m

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
29
Two sound waves, one wave is given by y1 = po sin (kx - t) and the other by y2 = po sin (kx - t + /2). The amplitude resulting from the interference of the two waves is
A) 2po
B)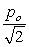
C) 1.25po
D)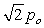
E) 0
A) 2po
B)
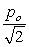
C) 1.25po
D)
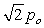
E) 0

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
30
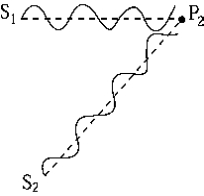 At P2 the waves from sources S1 and S2 shown in the figure
At P2 the waves from sources S1 and S2 shown in the figureA) are in phase.
B) have a path difference of one wavelength.
C) have a path difference of one-half wavelength.
D) are interfering constructively.
E) None of these is correct.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
31
Two speakers face each other at a distance of 1 m and are driven by a common audio oscillator. A first minimum in sound intensity is found 16.1 cm from the midpoint. If the velocity of sound is 330 m/s, find the frequency of the oscillator.
A) 256 Hz
B) 1024 Hz
C) 512 Hz
D) 341 Hz
E) 683 Hz
A) 256 Hz
B) 1024 Hz
C) 512 Hz
D) 341 Hz
E) 683 Hz

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
32
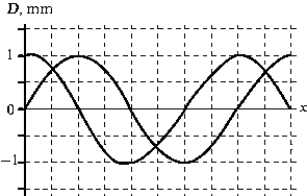 The figure shows two waves traveling in the positive-x direction. The amplitude of the resultant wave is
The figure shows two waves traveling in the positive-x direction. The amplitude of the resultant wave isA) 2.0 mm
B) 1.8 mm
C) 1.4 mm
D) 1.0 mm
E) 0.83 mm

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
33
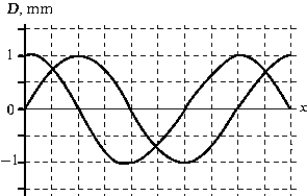
The figure shows two waves traveling in the positive-x direction. The phase difference between these two waves is
A) radians.
B) /2 radians.
C) /4 radians.
D) /8 radians.
E) /16 radians.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
34
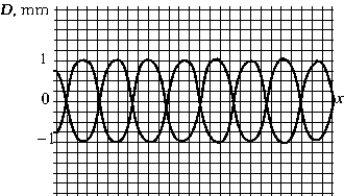 The figure shows two waves traveling in the positive-x direction. The amplitude of the resultant wave is
The figure shows two waves traveling in the positive-x direction. The amplitude of the resultant wave isA) 2.0 mm
B) 1.8 mm
C) 1.4 mm
D) 1.0 mm
E) zero

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
35
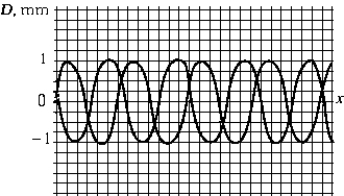 The figure shows two waves traveling in the positive-x direction. The phase difference between these two waves is closest to
The figure shows two waves traveling in the positive-x direction. The phase difference between these two waves is closest toA) 3.1 radians.
B) 1.6 radians.
C) 1.1 radians.
D) 2.4 radians.
E) 0.2 radians.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
36
Two sound waves, one wave is given by y1 = po sin ( 1t), and the other by y2 = po sin ( 2t), where 1 differs from 2 by a rad/s. The maximum sound intensity of the beat frequency is
A) po2
B) 2po2
C) 4po2
D) 8po2
A) po2
B) 2po2
C) 4po2
D) 8po2

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
37
Two sound waves, one wave is given by y1 = po sin (kx - t) and the other by y2 = po sin (kx - t + /4). The phase constant resulting from the interference of the two waves is
A) /8
B) /4
C) /2
D)
E) 0
A) /8
B) /4
C) /2
D)
E) 0

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
38
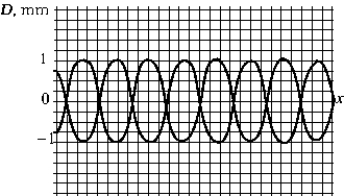
The figure shows two waves traveling in the positive-x direction. The phase difference between these two waves is
A) radians.
B) /2 radians.
C) /4 radians.
D) /8 radians.
E) /16 radians.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
39
Two sources are said to be coherent if
A) they are of the same frequency and has a phase of zero.
B) they are of the same frequency and maintain a constant non-zero phase.
C) they are of the same intensity but different frequency and has a phase of zero.
D) they are of the same intensity but different frequency and maintain a constant non-zero phase.
E) (A) and (B)
A) they are of the same frequency and has a phase of zero.
B) they are of the same frequency and maintain a constant non-zero phase.
C) they are of the same intensity but different frequency and has a phase of zero.
D) they are of the same intensity but different frequency and maintain a constant non-zero phase.
E) (A) and (B)

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
40
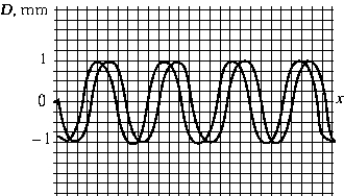 The figure shows two waves traveling in the positive-x direction. The amplitude of the resultant wave is closest to
The figure shows two waves traveling in the positive-x direction. The amplitude of the resultant wave is closest toA) 2.0 mm
B) 1.8 mm
C) 1.4 mm
D) 1.0 mm
E) zero

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
41
The fundamental frequency of a vibrating string is f1. If the tension in the string is doubled, the fundamental frequency becomes
A)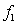 /2
/2
B) 11eaa4be_8550_d4cd_9e4a_9b9f5c46c44e_TB6080_11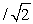
C) 11eaa4be_8550_d4cd_9e4a_9b9f5c46c44e_TB6080_11
D)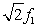
E) 211eaa4be_8550_d4cd_9e4a_9b9f5c46c44e_TB6080_11
A)
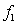 /2
/2B) 11eaa4be_8550_d4cd_9e4a_9b9f5c46c44e_TB6080_11
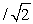
C) 11eaa4be_8550_d4cd_9e4a_9b9f5c46c44e_TB6080_11
D)
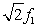
E) 211eaa4be_8550_d4cd_9e4a_9b9f5c46c44e_TB6080_11

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
42
A string whose length is 1 m is fixed at both ends and vibrates according to the equation
Y(x, t) = 0.04 sin x cos 2 t
Where the units are SI. The total number of nodes exhibited by the string is
A) 1
B) 2
C) 3
D) 4
E) 5
Y(x, t) = 0.04 sin x cos 2 t
Where the units are SI. The total number of nodes exhibited by the string is
A) 1
B) 2
C) 3
D) 4
E) 5

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
43
The fundamental frequency of a vibrating string is 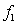 . If the tension in the string is decreased by 50% while the linear density is held constant, the fundamental frequency becomes
. If the tension in the string is decreased by 50% while the linear density is held constant, the fundamental frequency becomes
A) 0.511eaa4be_8550_d4cd_9e4a_9b9f5c46c44e_TB6080_11
B) 0.711eaa4be_8550_d4cd_9e4a_9b9f5c46c44e_TB6080_11
C) 0.911eaa4be_8550_d4cd_9e4a_9b9f5c46c44e_TB6080_11
D) 11eaa4be_8550_d4cd_9e4a_9b9f5c46c44e_TB6080_11
E) None of these is correct.
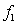 . If the tension in the string is decreased by 50% while the linear density is held constant, the fundamental frequency becomes
. If the tension in the string is decreased by 50% while the linear density is held constant, the fundamental frequency becomesA) 0.511eaa4be_8550_d4cd_9e4a_9b9f5c46c44e_TB6080_11
B) 0.711eaa4be_8550_d4cd_9e4a_9b9f5c46c44e_TB6080_11
C) 0.911eaa4be_8550_d4cd_9e4a_9b9f5c46c44e_TB6080_11
D) 11eaa4be_8550_d4cd_9e4a_9b9f5c46c44e_TB6080_11
E) None of these is correct.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
44
If the amplitude of a standing wave is doubled, the energy in the wave increases by a factor of
A)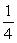
B)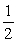
C) 1
D) 2
E) 4
A)
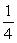
B)
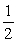
C) 1
D) 2
E) 4

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
45
The fundamental frequency of a vibrating string is 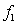 . If the tension in the string is quadrupled while the linear density is held constant, the fundamental frequency becomes
. If the tension in the string is quadrupled while the linear density is held constant, the fundamental frequency becomes
A) 11eaa4be_8550_d4cd_9e4a_9b9f5c46c44e_TB6080_11
B) 1.211eaa4be_8550_d4cd_9e4a_9b9f5c46c44e_TB6080_11
C) 1.511eaa4be_8550_d4cd_9e4a_9b9f5c46c44e_TB6080_11
D) 1.711eaa4be_8550_d4cd_9e4a_9b9f5c46c44e_TB6080_11
E) 211eaa4be_8550_d4cd_9e4a_9b9f5c46c44e_TB6080_11
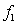 . If the tension in the string is quadrupled while the linear density is held constant, the fundamental frequency becomes
. If the tension in the string is quadrupled while the linear density is held constant, the fundamental frequency becomesA) 11eaa4be_8550_d4cd_9e4a_9b9f5c46c44e_TB6080_11
B) 1.211eaa4be_8550_d4cd_9e4a_9b9f5c46c44e_TB6080_11
C) 1.511eaa4be_8550_d4cd_9e4a_9b9f5c46c44e_TB6080_11
D) 1.711eaa4be_8550_d4cd_9e4a_9b9f5c46c44e_TB6080_11
E) 211eaa4be_8550_d4cd_9e4a_9b9f5c46c44e_TB6080_11

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
46
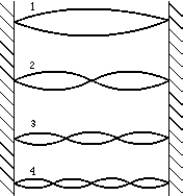 The figure shows several modes of vibration of a string fixed at both ends. The mode of vibration that represents the fifth harmonic is
The figure shows several modes of vibration of a string fixed at both ends. The mode of vibration that represents the fifth harmonic isA) 1
B) 2
C) 3
D) 4
E) None of these is correct.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
47
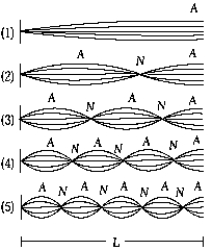 The figure represents a wire of length L, fixed at both ends, vibrating in several harmonics. The 3rd harmonic is shown in
The figure represents a wire of length L, fixed at both ends, vibrating in several harmonics. The 3rd harmonic is shown inA) 1
B) 2
C) 3
D) 4
E) 5

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
48
A microphone is placed at the node of a standing sound wave. What does the microphone pick up?
A) A constant and very high intensity sound.
B) A constant and very low intensity sound.
C) A varying high intensity sound.
D) A varying low intensity sound.
E) Unable to tell.
A) A constant and very high intensity sound.
B) A constant and very low intensity sound.
C) A varying high intensity sound.
D) A varying low intensity sound.
E) Unable to tell.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
49
Which of the following equations represents a standing wave? (The symbols have their usual meaning.)
A)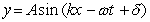
B)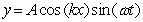
C)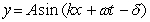
D)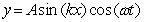
E) (B) and (D)
A)
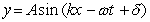
B)
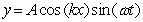
C)
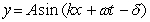
D)
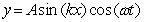
E) (B) and (D)

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
50
If both the tension and the length of a vibrating string are doubled while the linear density remains constant, the fundamental frequency of the string is multiplied by
A) 1
B) 2
C)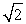
D)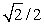
E)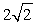
A) 1
B) 2
C)
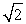
D)
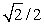
E)
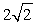

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
51
 The two progressive waves are moving with equal velocities and wavelengths but in opposite directions in the string. Which of the following gives all of the points that will be nodes in the resultant standing wave?
The two progressive waves are moving with equal velocities and wavelengths but in opposite directions in the string. Which of the following gives all of the points that will be nodes in the resultant standing wave?A) 2, 4, 6, 8, and 10
B) 2, 6, and 10
C) 1, 5, and 9
D) 3 and 7
E) 1, 3, 5, 7, and 9

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
52
The fundamental frequency of a vibrating string is f1. If the tension in the string is increased by 50% while the linear density is held constant, the fundamental frequency becomes
A)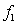
B) 1.211eaa4be_8550_d4cd_9e4a_9b9f5c46c44e_TB6080_11
C) 1.511eaa4be_8550_d4cd_9e4a_9b9f5c46c44e_TB6080_11
D) 1.711eaa4be_8550_d4cd_9e4a_9b9f5c46c44e_TB6080_11
E) 211eaa4be_8550_d4cd_9e4a_9b9f5c46c44e_TB6080_11
A)
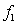
B) 1.211eaa4be_8550_d4cd_9e4a_9b9f5c46c44e_TB6080_11
C) 1.511eaa4be_8550_d4cd_9e4a_9b9f5c46c44e_TB6080_11
D) 1.711eaa4be_8550_d4cd_9e4a_9b9f5c46c44e_TB6080_11
E) 211eaa4be_8550_d4cd_9e4a_9b9f5c46c44e_TB6080_11

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
53
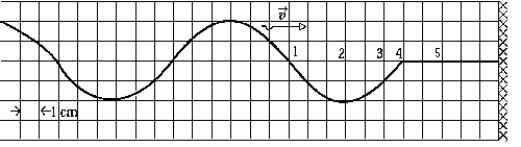 The figure shows a wave on a string approaching its fixed end at a wall. When the wave reaches the wall and is reflected, a standing wave will be set up in the string. One of the antinodes in the standing wave will be found at position
The figure shows a wave on a string approaching its fixed end at a wall. When the wave reaches the wall and is reflected, a standing wave will be set up in the string. One of the antinodes in the standing wave will be found at positionA) 1
B) 2
C) 3
D) 4
E) 5

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
54
A standing wave is shown in the figure on the right. If the period of the wave is T, the shortest time it takes for the wave to go from the solid curve to the dashed curve is 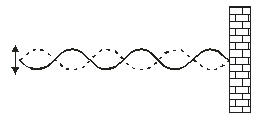
A) T/4
B) T/3
C) T/2
D) 3T/4
E) None of these is correct.

A) T/4
B) T/3
C) T/2
D) 3T/4
E) None of these is correct.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
55
A string of linear density and length L is under a constant tension T = mg. One end of the string is attached to a tunable harmonic oscillator. A resonant standing wave is observed 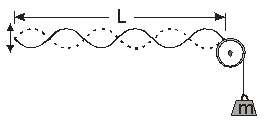
A) at any frequency.
B) when the frequency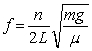 where n = 1, 2, 3, ...
where n = 1, 2, 3, ...
C) when the frequency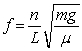 where n = 1, 2, 3, ...
where n = 1, 2, 3, ...
D) when the frequency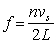 where n = 1, 2, 3, ...and vs is the speed of sound.
where n = 1, 2, 3, ...and vs is the speed of sound.
E) unable to tell

A) at any frequency.
B) when the frequency
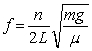 where n = 1, 2, 3, ...
where n = 1, 2, 3, ...C) when the frequency
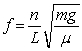 where n = 1, 2, 3, ...
where n = 1, 2, 3, ...D) when the frequency
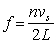 where n = 1, 2, 3, ...and vs is the speed of sound.
where n = 1, 2, 3, ...and vs is the speed of sound.E) unable to tell

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
56
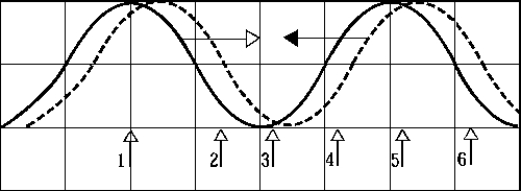 One wave moves to the right and a second wave (reflected) moves to the left to form a stationary wave. At which point(s) does the stationary wave have a node?
One wave moves to the right and a second wave (reflected) moves to the left to form a stationary wave. At which point(s) does the stationary wave have a node?A) 1
B) 3 and 5
C) 2
D) 4 and 6
E) 2, 4, and 6

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
57
Four pendulums are hung from a light rod that is free to rotate about its long axis. The pendulums have lengths L, 2L, L/2 and L, and masses m, m/2, 2m and 4m respectively. Pendulum 1 is set to swing at its natural frequency. Which of the other three will, over time, also oscillate at the same frequency? 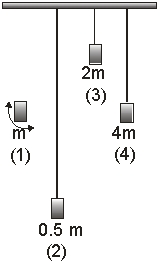
A) (2)
B) (3)
C) (4)
D) (2) and (3)
E) all three

A) (2)
B) (3)
C) (4)
D) (2) and (3)
E) all three

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
58
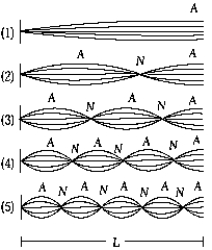 The figure represents a wire of length L, fixed at both ends, vibrating in several harmonics. The 7th harmonic is shown in
The figure represents a wire of length L, fixed at both ends, vibrating in several harmonics. The 7th harmonic is shown inA) 1
B) 2
C) 3
D) 4
E) 5

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
59
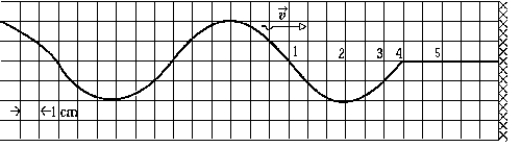 The figure shows a wave on a string approaching its fixed end at a wall. When the wave reaches the wall and is reflected, a standing wave is set up in the string. One will observe a node at position
The figure shows a wave on a string approaching its fixed end at a wall. When the wave reaches the wall and is reflected, a standing wave is set up in the string. One will observe a node at positionA) 1
B) 2
C) 3
D) 4
E) 5

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
60
A standing wave is created by oscillating a taut string at a frequency that corresponds to one of the resonant frequencies. The amplitude of the antinodes is very much larger than the amplitude of the oscillator. Does this violate the conservation of energy principle? Explain why. 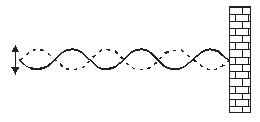
A) Yes, since E is proportional to amplitude squared.
B) Yes, since there is large kinetic energy of the string, and this is much bigger than the energy from the oscillator.
C) No, energy from waves does not obey the conservation of energy principle in the first place.
D) No, the energy at the antinodes builds up after the first few cycles, after which the dissipation due to friction equals the energy supplied by the oscillator.
E) Whether it obeys the conservation of energy principle depends on the tension in the string.

A) Yes, since E is proportional to amplitude squared.
B) Yes, since there is large kinetic energy of the string, and this is much bigger than the energy from the oscillator.
C) No, energy from waves does not obey the conservation of energy principle in the first place.
D) No, the energy at the antinodes builds up after the first few cycles, after which the dissipation due to friction equals the energy supplied by the oscillator.
E) Whether it obeys the conservation of energy principle depends on the tension in the string.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
61
 The air column in an organ pipe, which is closed at one end, is vibrating in such a way as to produce the second harmonic. A pressure node and displacement node, respectively, occur at
The air column in an organ pipe, which is closed at one end, is vibrating in such a way as to produce the second harmonic. A pressure node and displacement node, respectively, occur atA) 1 and 3
B) 1 and 5
C) 7 and 4
D) 7 and 5
E) 5 and 3

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
62
A string fixed at both ends is driven by a tuning fork to produce standing waves. If the tension in the string is increased,
A) the frequency increases.
B) the frequency decreases and the wave velocity remains constant.
C) the wavelength decreases.
D) the wave velocity increases.
E) the wave velocity decreases.
A) the frequency increases.
B) the frequency decreases and the wave velocity remains constant.
C) the wavelength decreases.
D) the wave velocity increases.
E) the wave velocity decreases.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
63
A string 2.0 m long has a mass of 2.4 10-2 kg. When fixed at both ends, it vibrates with a fundamental frequency of 150 Hz. The speed of a transverse wave in the string is
A) 3.6 m/s
B) 75 m/s
C) 0.30 km/s
D) 0.60 km/s
E) 0.63 km/s
A) 3.6 m/s
B) 75 m/s
C) 0.30 km/s
D) 0.60 km/s
E) 0.63 km/s

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
64
 A stretched string is fixed at points 1 and 5. When it is vibrating in its first harmonic frequency, the nodes are at points
A stretched string is fixed at points 1 and 5. When it is vibrating in its first harmonic frequency, the nodes are at pointsA) 1 and 5 only.
B) 1, 3, and 5.
C) 2 and 4.
D) 2, 3, and 4.
E) 1, 2, 3, 4, and 5.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
65
A vibrating tuning fork of frequency 640 Hz is held above a tube filled with water. Assume the speed of sound to be 330 m/s. As the water level is lowered, consecutive maxima in intensity are observed at intervals of about
A) 12.9 cm
B) 19.4 cm
C) 25.8 cm
D) 51.7 cm
E) 194 cm
A) 12.9 cm
B) 19.4 cm
C) 25.8 cm
D) 51.7 cm
E) 194 cm

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
66
A stretched string of length L, fixed at both ends, is vibrating in its third harmonic. How far from the end of the string can the blade of a screwdriver be placed against the string without disturbing the amplitude of the vibration?
A) L/6
B) L/4
C) L/5
D) L/2
E) None of these is correct.
A) L/6
B) L/4
C) L/5
D) L/2
E) None of these is correct.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
67
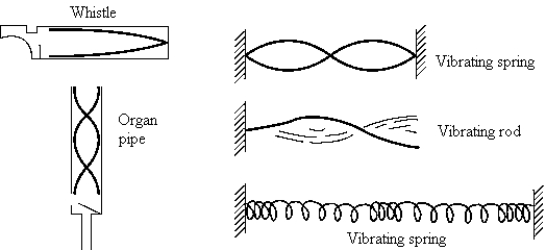 Of the sound sources shown, that which is vibrating with its first harmonic is the
Of the sound sources shown, that which is vibrating with its first harmonic is theA) whistle.
B) organ pipe.
C) vibrating string.
D) vibrating rod.
E) vibrating spring.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
68
On a standing-wave pattern, the distance between two consecutive nodes is d. The wavelength is
A) d/2
B) d
C) 3d/2
D) 2d
E) 4d
A) d/2
B) d
C) 3d/2
D) 2d
E) 4d

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
69
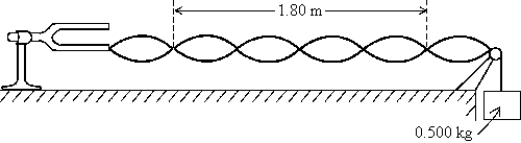
A string is connected to a tuning fork whose frequency is 80.0 Hz and is held under tension by 0.500 kg. The tuning fork causes the string to vibrate as shown. The mass per unit length for the string is
A) 9.45 10-4 kg/m
B) 6.80 10-3 kg/m
C) 4.34 kg/m
D) 6.00 10-3 kg/m
E) 3.85 10-2 kg/m

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
70
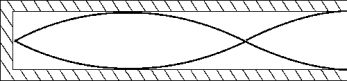 The air in a closed organ pipe vibrates as shown. The length of the pipe is 3.0 m. The frequency of vibration is 80 Hz. The speed of sound in the pipe is approximately
The air in a closed organ pipe vibrates as shown. The length of the pipe is 3.0 m. The frequency of vibration is 80 Hz. The speed of sound in the pipe is approximatelyA) 80 m/s
B) 0.16 km/s
C) 0.24 km/s
D) 0.32 km/s
E) 0.96 km/s

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
71
The figure shows a standing wave in a pipe that is closed at one end. The frequency associated with this wave pattern is called the 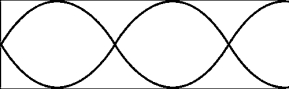
A) first harmonic.
B) second harmonic.
C) third harmonic.
D) fourth harmonic.
E) fifth harmonic.

A) first harmonic.
B) second harmonic.
C) third harmonic.
D) fourth harmonic.
E) fifth harmonic.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
72
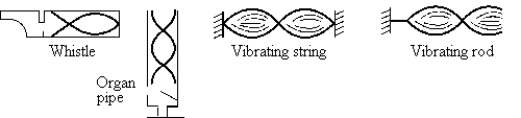 Of the sound sources shown, that which is vibrating with its first harmonic is
Of the sound sources shown, that which is vibrating with its first harmonic isA) the whistle.
B) the organ pipe.
C) the vibrating string.
D) the vibrating rod.
E) None of these is correct.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
73
In a pipe that is open at one end and closed at the other and that has a fundamental frequency of 256 Hz, which of the following frequencies cannot be produced?
A) 768 Hz
B) 1.28 kHz
C) 5.12 kHz
D) 19.7 kHz
E) all of these can be produced
A) 768 Hz
B) 1.28 kHz
C) 5.12 kHz
D) 19.7 kHz
E) all of these can be produced

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
74
When an organ pipe, which is closed at one end only, vibrates with a frequency that is three times its fundamental (first harmonic) frequency,
A) the sound produced travels at three times its former speed.
B) the sound produced is its fifth harmonic.
C) beats are produced.
D) the sound produced has one-third its former wavelength.
E) the closed end is a displacement antinode.
A) the sound produced travels at three times its former speed.
B) the sound produced is its fifth harmonic.
C) beats are produced.
D) the sound produced has one-third its former wavelength.
E) the closed end is a displacement antinode.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
75
A vibrating tuning fork of frequency 1080 Hz is held above a tube filled with water. Assume the speed of sound to be 330 m/s. As the water level is lowered, consecutive maxima in intensity are observed at intervals of about
A) 7.65 cm
B) 15.3 cm
C) 23.0 cm
D) 30.6 cm
E) 53.6 cm
A) 7.65 cm
B) 15.3 cm
C) 23.0 cm
D) 30.6 cm
E) 53.6 cm

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
76
In a vibrating-string experiment, three loops are observed between points A and B when the mass on one end of the string is 100 g. The number of loops between A and B can be changed to two by replacing the 100-g mass with a mass of 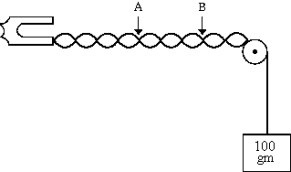
A) 150 g
B) 225 g
C) 44.4 g
D) 66.7 g
E) 300 g

A) 150 g
B) 225 g
C) 44.4 g
D) 66.7 g
E) 300 g

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
77
A string fixed at both ends is vibrating in a standing wave. There are three nodes between the ends of the string, not including those on the ends. The string is vibrating at a frequency that is its
A) fundamental.
B) second harmonic.
C) third harmonic.
D) fourth harmonic.
E) fifth harmonic.
A) fundamental.
B) second harmonic.
C) third harmonic.
D) fourth harmonic.
E) fifth harmonic.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
78
 A stretched string is fixed at points 1 and 5. When it is vibrating at the second harmonic frequency, the nodes of the standing wave are at points
A stretched string is fixed at points 1 and 5. When it is vibrating at the second harmonic frequency, the nodes of the standing wave are at pointsA) 1 and 5.
B) 1, 3, and 5.
C) 1 and 3.
D) 2 and 4.
E) 1, 2, 3, 4, and 5.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
79
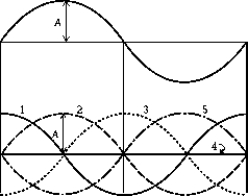 A stationary wave of amplitude A and period T exists in a rope. At a particular instant, the configuration of the rope is as shown. At an instant
A stationary wave of amplitude A and period T exists in a rope. At a particular instant, the configuration of the rope is as shown. At an instant 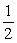 T later, the configuration of the rope is
T later, the configuration of the rope isA) 1
B) 2
C) 3
D) 4
E) 5

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
80
A string 2.0 m long has a mass of 2.4 10-2 kg. When fixed at both ends, it vibrates with a fundamental frequency of 150 Hz. The frequency of the third harmonic of this fundamental is
A) 50 Hz
B) 75 Hz
C) 0.15 kHz
D) 0.45 kHz
E) 1.1 kHz
A) 50 Hz
B) 75 Hz
C) 0.15 kHz
D) 0.45 kHz
E) 1.1 kHz

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck


