Deck 12: Binomial Distributions
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/39
Play
Full screen (f)
Deck 12: Binomial Distributions
1
Suppose X is a random variable with the binomial distribution with n = 4 and p = 1/4. The probability that X is greater than or equal to 1 is:
A)0.9961.
B)0.6836.
C)0.3164.
D)0.0039.
A)0.9961.
B)0.6836.
C)0.3164.
D)0.0039.
0.6836.
2
A local veterinary clinic typically sees 15% of its horses presenting with West Nile virus. Last month, 100 horses were admitted and 20 of them had been infected with West Nile virus. The probability of seeing 20 or more horses with West Nile virus was calculated based on a Normal distribution with = 15 and = 12.75. Which of the following statements is true?
A)Using the Normal approximation to the binomial distribution is justified, because X = 20 > 10.
B)Using the Normal approximation to the binomial distribution is justified, because n is large and exact calculations are too tedious.
C)Using the Normal approximation to the binomial distribution is justified, because np = 15 and n(1 - p)= 85.
D)All of the answer options are correct.
A)Using the Normal approximation to the binomial distribution is justified, because X = 20 > 10.
B)Using the Normal approximation to the binomial distribution is justified, because n is large and exact calculations are too tedious.
C)Using the Normal approximation to the binomial distribution is justified, because np = 15 and n(1 - p)= 85.
D)All of the answer options are correct.
All of the answer options are correct.
3
A local veterinary clinic recently had 25 horses admitted from the same barn. It was determined that most cases of West Nile virus infection in the group of 25 horses were caused by infection by another horse. In this case, modeling the number of cases diagnosed with a binomial distribution is not appropriate because:
A)the success on different trials needs to be mutually exclusive and this is not the case here.
B)the success on individual trials needs to be independent.
C)the success on individual trials needs to be positive.
D)n = 25 is a very small sample.
A)the success on different trials needs to be mutually exclusive and this is not the case here.
B)the success on individual trials needs to be independent.
C)the success on individual trials needs to be positive.
D)n = 25 is a very small sample.
the success on individual trials needs to be independent.
4
A local veterinary clinic typically sees 15% of its horses presenting with West Nile virus. If 10 horses are admitted during July, what is the probability at least one of the 10 horses has been infected with West Nile virus?
A)0.923
B)0.177
C)0.348
D)0.803
A)0.923
B)0.177
C)0.348
D)0.803

Unlock Deck
Unlock for access to all 39 flashcards in this deck.
Unlock Deck
k this deck
5
A local veterinary clinic typically sees 15% of its horses presenting with West Nile virus. If 10 horses are admitted during July, what is the probability a randomly selected horse among the 10 new admits has West Nile virus?
A)0.1
B)0.5
C)0.15
D)0.9
A)0.1
B)0.5
C)0.15
D)0.9

Unlock Deck
Unlock for access to all 39 flashcards in this deck.
Unlock Deck
k this deck
6
Two students taking a multiple choice exam with 20 questions and four choices for each question have the same incorrect answer on seven of eight incorrectly answered problems. The probability that student B guesses the same incorrect answer as student A on a particular question is 1/4. If the student is guessing, the guess for one problem is independent of the guess for the other problems. The probability of getting agreement on seven or more out of eight questions is:
A)0.9996.
B)0.0004.
C)0.25.
D)None of the answer options is correct.
A)0.9996.
B)0.0004.
C)0.25.
D)None of the answer options is correct.

Unlock Deck
Unlock for access to all 39 flashcards in this deck.
Unlock Deck
k this deck
7
Suppose we toss a fair coin repeatedly. We continue to do this until a tail is observed. Let X be the number of tosses required. Then X has:
A)a binomial distribution, with mean 0.5.
B)a binomial distribution, with mean 2.
C)a binomial distribution, with variance 0.707.
D)None of the answer options is correct.
A)a binomial distribution, with mean 0.5.
B)a binomial distribution, with mean 2.
C)a binomial distribution, with variance 0.707.
D)None of the answer options is correct.

Unlock Deck
Unlock for access to all 39 flashcards in this deck.
Unlock Deck
k this deck
8
Two students taking a multiple choice exam with 20 questions and four choices for each question have the same incorrect answer on eight of the problems. The probability that student B guesses the same incorrect answer as student A on a particular question is 1/4. If the student is guessing, it is reasonable to assume guesses for different problems are independent. The instructor for the class suspects the students exchanged answers. The teacher decides to present a statistical argument to substantiate the accusation. A possible model for the number of incorrect questions that agree is:
A)a binomial distribution with n = 8 and p = 0.25.
B)a binomial distribution with n = 20 and p = 0.4.
C)a Normal distribution with = 8 and = 0.25.
D)a Normal distribution with = 20 and = 0.4.
A)a binomial distribution with n = 8 and p = 0.25.
B)a binomial distribution with n = 20 and p = 0.4.
C)a Normal distribution with = 8 and = 0.25.
D)a Normal distribution with = 20 and = 0.4.

Unlock Deck
Unlock for access to all 39 flashcards in this deck.
Unlock Deck
k this deck
9
A college basketball player makes 70% of his free throws. At the end of a game, his team is losing by two points. He is fouled attempting a three-point shot and is awarded three free throws. Assuming each free throw is independent, what is the probability that he makes at least two of the free throws?
A)0.784
B)0.7
C)0.441
D)0.216
A)0.784
B)0.7
C)0.441
D)0.216

Unlock Deck
Unlock for access to all 39 flashcards in this deck.
Unlock Deck
k this deck
10
Opinion polls find that 20% of American adults claim they never have time to relax. Suppose you take a random sample of 200 American adults, and you count the number X in your sample that claim they never have time to relax. Using the Normal approximation, the probability that X is at least 50 is:
A)less than 0.0001.
B)about 0.962.
C)about 0.2.
D)about 0.038.
A)less than 0.0001.
B)about 0.962.
C)about 0.2.
D)about 0.038.

Unlock Deck
Unlock for access to all 39 flashcards in this deck.
Unlock Deck
k this deck
11
At a large Midwestern college, 4% of the students are Hispanic. A random sample of 20 students from the college is selected. Let X denote the number of Hispanics among them. The standard deviation of X is:
A)0.71
B)0.768.
C)0.8.
D)0.88.
A)0.71
B)0.768.
C)0.8.
D)0.88.

Unlock Deck
Unlock for access to all 39 flashcards in this deck.
Unlock Deck
k this deck
12
Two students taking a multiple choice exam with 20 questions and four choices for each question have the same incorrect answer on seven of eight incorrectly answered problems. The probability that student B guesses the same incorrect answer as student A on a particular question is 1/4. If the student is guessing, the guess for one problem is independent of the guess for the other problems. The number of guesses by student B that agree with those of student A has mean and variance given by:
A) = 2 and 2 = 1.5.
B) = 2 and 2 = 1.52.
C) = 4 and 2 = 1.5.
D) = 2 and = 1.5.
A) = 2 and 2 = 1.5.
B) = 2 and 2 = 1.52.
C) = 4 and 2 = 1.5.
D) = 2 and = 1.5.

Unlock Deck
Unlock for access to all 39 flashcards in this deck.
Unlock Deck
k this deck
13
For which of the following counts would a binomial probability model be reasonable?
A)the number of phone calls received in a one-hour period
B)the number of hearts in a hand of five cards dealt from a standard deck of 52 cards that has been thoroughly shuffled
C)the number of sevens in a randomly selected set of five digits from your table of random digits
D)All of the answer options are correct.
A)the number of phone calls received in a one-hour period
B)the number of hearts in a hand of five cards dealt from a standard deck of 52 cards that has been thoroughly shuffled
C)the number of sevens in a randomly selected set of five digits from your table of random digits
D)All of the answer options are correct.

Unlock Deck
Unlock for access to all 39 flashcards in this deck.
Unlock Deck
k this deck
14
Suppose we select an SRS of size n = 100 from a large population having proportion p of successes. Let X be the number of successes in the sample. For which value of p would it be safe to assume the sampling distribution of X is approximately Normal?
A)0.01
B)1/9
C)0.975
D)0.9999
A)0.01
B)1/9
C)0.975
D)0.9999

Unlock Deck
Unlock for access to all 39 flashcards in this deck.
Unlock Deck
k this deck
15
At a large Midwestern college, 4% of the students are Hispanic. A random sample of 20 students from the college is selected. Let X denote the number of Hispanics among them. The mean of X is:
A)0.4.
B)0.8.
C)1.2.
D)1.6.
A)0.4.
B)0.8.
C)1.2.
D)1.6.

Unlock Deck
Unlock for access to all 39 flashcards in this deck.
Unlock Deck
k this deck
16
A small class has 10 students. Seven of the students are male and three are female. You write the name of each student on a small card. The cards are shuffled thoroughly, and you choose one at random, observe the name of the student, and replace it in the set. The cards are thoroughly reshuffled, and you again choose a card at random, observe the name, and replace it in the set. This is done a total of five times. Let X be the number of cards observed in these five trials with a name corresponding to a male student. The random variable X has which of the following probability distributions?
A)the Normal distribution, with mean 3 and variance 1
B)the binomial distribution, with parameters n = 5 and p = 0.3
C)the binomial distribution, with parameters n = 5 and p = 0.7
D)None of the answer options is correct.
A)the Normal distribution, with mean 3 and variance 1
B)the binomial distribution, with parameters n = 5 and p = 0.3
C)the binomial distribution, with parameters n = 5 and p = 0.7
D)None of the answer options is correct.

Unlock Deck
Unlock for access to all 39 flashcards in this deck.
Unlock Deck
k this deck
17
A local veterinary clinic typically sees 15% of its horses presenting with West Nile virus. If 10 horses are admitted during July, what is the probability that 2 or fewer horses among the 10 horses admitted have been infected with West Nile virus?
A)0.8202
B)0.1937
C)0.3874
D)0.3487
A)0.8202
B)0.1937
C)0.3874
D)0.3487

Unlock Deck
Unlock for access to all 39 flashcards in this deck.
Unlock Deck
k this deck
18
If X has a binomial distribution with 20 trials and a mean of 6, then the success probability p is:
A)0.3.
B)0.5.
C)0.75.
D)This cannot be determined without taking a sample.
A)0.3.
B)0.5.
C)0.75.
D)This cannot be determined without taking a sample.

Unlock Deck
Unlock for access to all 39 flashcards in this deck.
Unlock Deck
k this deck
19
At a large Midwestern college, 4% of the students are Hispanic. A random sample of 20 students from the college is selected. Let X denote the number of Hispanics among them. The probability that X is at least 1 is:
A)0.22.
B)0.44.
C)0.56.
D)0.77.
A)0.22.
B)0.44.
C)0.56.
D)0.77.

Unlock Deck
Unlock for access to all 39 flashcards in this deck.
Unlock Deck
k this deck
20
Which of the following statements is not true about the binomial distribution?
A)A random variable having a binomial distribution is a finite count, and the minimum value is zero.
B)The smallest value can be zero or an integer above zero.
C)The overall experiment consists of independent and identical trials.
D)The mean does not have to be an integer, even though the variable is a count.
A)A random variable having a binomial distribution is a finite count, and the minimum value is zero.
B)The smallest value can be zero or an integer above zero.
C)The overall experiment consists of independent and identical trials.
D)The mean does not have to be an integer, even though the variable is a count.

Unlock Deck
Unlock for access to all 39 flashcards in this deck.
Unlock Deck
k this deck
21
Which of the following statements is true about a binomial experiment?
A)The number of trials can vary.
B)There are only two possible outcomes: success and failure.
C)The probability of success and failure can change from trial to trial.
D)Each trial in the experiment may depend on previous trials.
A)The number of trials can vary.
B)There are only two possible outcomes: success and failure.
C)The probability of success and failure can change from trial to trial.
D)Each trial in the experiment may depend on previous trials.

Unlock Deck
Unlock for access to all 39 flashcards in this deck.
Unlock Deck
k this deck
22
A study investigated the use of social media by freshman. One question asked if the person answering ever stayed up late to chat with friends and ended up sleep deprived. It was thought that at least 80% of all people of freshman age would stay up late. If the study sampled 400 students, what is the mean number of students staying up late in random samples of n = 400 in the freshman population?
A)80
B)160
C)240
D)320
A)80
B)160
C)240
D)320

Unlock Deck
Unlock for access to all 39 flashcards in this deck.
Unlock Deck
k this deck
23
A study investigated the use of social media by freshman. One question asked if the person answering ever stayed up late to chat with friends and ended up sleep deprived. It was thought that at least 80% of all people of freshman age would stay up late. If the study sampled 400 students, which of the following statements is true?
A)The number of students in the sample who stay up late follows a binomial distribution with = 320 and variance 2 = 64.
B)The number of students in the sample who stay up late can be approximated by a Normal distribution with mean = 320 and variance 2 = 64.
C)The number of students in the sample who stay up late can be approximated by a Normal distribution with mean = 320 and standard deviation = 8.
D)All of the answer options are correct.
A)The number of students in the sample who stay up late follows a binomial distribution with = 320 and variance 2 = 64.
B)The number of students in the sample who stay up late can be approximated by a Normal distribution with mean = 320 and variance 2 = 64.
C)The number of students in the sample who stay up late can be approximated by a Normal distribution with mean = 320 and standard deviation = 8.
D)All of the answer options are correct.

Unlock Deck
Unlock for access to all 39 flashcards in this deck.
Unlock Deck
k this deck
24
A local politician claims that one in five automobile accidents involve a teenage driver. He is advocating increasing the age at which teenagers can drive alone. Over a two-month period there are 67 accidents in your city, and only nine of them involve a teenage driver. If the politician is correct, what is the chance that you would observe nine or fewer accidents involving a teenage driver?
A)about 0.05
B)about 0.09
C)about 0.16
D)about 0.11
A)about 0.05
B)about 0.09
C)about 0.16
D)about 0.11

Unlock Deck
Unlock for access to all 39 flashcards in this deck.
Unlock Deck
k this deck
25
Zener cards are often used to test the psychic ability of individuals. In the Zener deck, there are five different patterns displayed and each has a 1/5 probability of being drawn from a well-shuffled deck. The five patterns are: circle, plus sign, wavy lines, empty box, and star. One hundred trials were conducted, and your very impressive friend guessed right on 41 of those trials. Given this sample, can we use the Normal approximation to the binomial?
A)Yes, because np 10.
B)Yes, because np 10 and n(1 - p) 10.
C)No, because n(1 - p) 10.
D)No, because np 10 and n(1 - p) 10.
A)Yes, because np 10.
B)Yes, because np 10 and n(1 - p) 10.
C)No, because n(1 - p) 10.
D)No, because np 10 and n(1 - p) 10.

Unlock Deck
Unlock for access to all 39 flashcards in this deck.
Unlock Deck
k this deck
26
A college basketball player makes 80% of his free throws. Over the course of the season, he will attempt 100 free throws. Assuming free-throw attempts are independent, what is the probability that he makes at least 90 of these attempts?
A)about 0.9
B)about 0.7
C)about 0.3
D)about 0.006
A)about 0.9
B)about 0.7
C)about 0.3
D)about 0.006

Unlock Deck
Unlock for access to all 39 flashcards in this deck.
Unlock Deck
k this deck
27
A very large gardening business grows rose bushes for sale to garden stores around the world. The most popular colors are red, pink, and white. The business decides on 50% red roses, 30% pink, and 20% white. A gardener orders 10 rose bushes selected randomly from a huge field. Her primary interest is in pink roses. Assuming rose bushes are selected independently, the number of pink rose bushes can be modeled by a binomial distribution. The probability of getting 1 pink rose bush is:
A)p = 0.5.
B)p = 0.8.
C)p = 0.3.
D)p = 0.2.
A)p = 0.5.
B)p = 0.8.
C)p = 0.3.
D)p = 0.2.

Unlock Deck
Unlock for access to all 39 flashcards in this deck.
Unlock Deck
k this deck
28
Twenty percent of American households own three or more cars. A random sample of 144 American households is selected. Let X be the number of households selected that own three or more cars. Using the Normal approximation, the probability that at least 34 of the households selected own at least three or more cars is:
A)0.14.
B)0.409.
C)0.591.
D)0.86.
A)0.14.
B)0.409.
C)0.591.
D)0.86.

Unlock Deck
Unlock for access to all 39 flashcards in this deck.
Unlock Deck
k this deck
29
A hobby gardener planted 20 rose bushes, 8 of which produced red roses and the other 12 produced white roses. The gardener randomly samples 5 rose bushes to be treated with a new plant food. He wants to calculate the probability that only white rose bushes get selected. Which of the following distributions can he use to calculate this probability?
A)the Normal distribution
B)the binomial distribution
C)the Normal approximation to the binomial distribution
D)None of the answer options is correct.
A)the Normal distribution
B)the binomial distribution
C)the Normal approximation to the binomial distribution
D)None of the answer options is correct.

Unlock Deck
Unlock for access to all 39 flashcards in this deck.
Unlock Deck
k this deck
30
An experiment consisted of 10 draws with replacement from an urn containing four red marbles and six green marbles. The probability that there are at least three and at most six red marbles is:
A)0.563.
B)0.778.
C)0.605.
D)0.82.
A)0.563.
B)0.778.
C)0.605.
D)0.82.

Unlock Deck
Unlock for access to all 39 flashcards in this deck.
Unlock Deck
k this deck
31
Suppose a flu epidemic is sweeping a campus and many students are sick. Student health services finds that 30% of students are ill. A nurse samples a dormitory with 30 students and wants to calculate the probability that at least 10 students are sick. Which of the following statements is false?
A)The binomial distribution cannot be used in this example, because the probability that 1 student is sick is not independent of another student in the dorm also being sick.
B)The Normal approximation to the binomial cannot be used, because the binomial distribution is not an appropriate model.
C)The Normal approximation to the binomial could not be used, even if the binomial were an appropriate model, because np = 30 × 0.3 = 9 and this violates one criterion for using the Normal approximation.
D)The binomial distribution can be used here, because our variable of interest is a finite count with minimum 0 and maximum 30.
A)The binomial distribution cannot be used in this example, because the probability that 1 student is sick is not independent of another student in the dorm also being sick.
B)The Normal approximation to the binomial cannot be used, because the binomial distribution is not an appropriate model.
C)The Normal approximation to the binomial could not be used, even if the binomial were an appropriate model, because np = 30 × 0.3 = 9 and this violates one criterion for using the Normal approximation.
D)The binomial distribution can be used here, because our variable of interest is a finite count with minimum 0 and maximum 30.

Unlock Deck
Unlock for access to all 39 flashcards in this deck.
Unlock Deck
k this deck
32
A very large gardening business grows rose bushes for sale to garden stores around the world. The most popular colors are red, pink, and white. The business decides on 50% red roses, 30% pink, and 20% white. A gardener orders 10 rose bushes selected randomly from a huge field. Her primary interest is in pink roses. A good model for the number of bushes with pink roses is given by the binomial distribution. Probability calculations are quicker when using the Normal approximation to the binomial distribution. Which of the following is false?
A)The approximation requires np 10 and n(1 - p) 10.
B)The sample size here is too small to use the Normal approximation to the binomial.
C)The approximation requires np 30.
D)The Normal approximation works better if the success probability p is close to p = 0.5.
A)The approximation requires np 10 and n(1 - p) 10.
B)The sample size here is too small to use the Normal approximation to the binomial.
C)The approximation requires np 30.
D)The Normal approximation works better if the success probability p is close to p = 0.5.

Unlock Deck
Unlock for access to all 39 flashcards in this deck.
Unlock Deck
k this deck
33
A group of economists surveys consumers of smartphones to see which devices consumers prefer. The question asked of shoppers is whether they are purchasing a Windows device or another type. The economists count the number of shoppers expressing preference for a Windows device. The survey samples about 50 shoppers from among several million. Which of the following criteria is violated regarding a binomial model?
A)There are more than two possibilities for smartphones, and the binomial allows only two categories: success and failure.
B)This is sampling without replacement and, therefore, the observations are dependent despite the large population.
C)The binomial has to be a finite count between zero and some fixed upper value.
D)None of the criteria listed is violated.
A)There are more than two possibilities for smartphones, and the binomial allows only two categories: success and failure.
B)This is sampling without replacement and, therefore, the observations are dependent despite the large population.
C)The binomial has to be a finite count between zero and some fixed upper value.
D)None of the criteria listed is violated.

Unlock Deck
Unlock for access to all 39 flashcards in this deck.
Unlock Deck
k this deck
34
A college basketball player makes 5/6 of his free throws. Assuming free throws are independent, the probability that he makes exactly three of his next four free throws is:
A)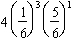 .
.
B)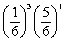 .
.
C)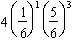 .
.
D)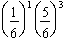 .
.
A)
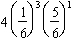 .
.B)
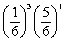 .
.C)
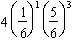 .
.D)
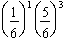 .
.
Unlock Deck
Unlock for access to all 39 flashcards in this deck.
Unlock Deck
k this deck
35
An article in Parenting magazine reported that 60% of Americans needed a vacation after visiting their families for the holidays. Suppose this is the true proportion of Americans who feel this way. A random sample of 100 Americans is taken. Using the Normal approximation, what is the probability that less than 50% of the people in the sample feel that they need a vacation after visiting their families for the holidays?
A)0.4
B)0.1446
C)0.0207
D)0.0062
A)0.4
B)0.1446
C)0.0207
D)0.0062

Unlock Deck
Unlock for access to all 39 flashcards in this deck.
Unlock Deck
k this deck
36
Zener cards are often used to test the psychic ability of individuals. In the Zener deck, there are five different patterns displayed and each has a 1/5 probability of being drawn from a well-shuffled deck. The five patterns are: circle, plus sign, wavy lines, empty box, and star. One hundred trials were conducted, and your very impressive friend guessed right on 41 of those trials. What proportion of the cards would I expect my friend to guess correctly?
A)0%
B)20%
C)80%
D)100%
A)0%
B)20%
C)80%
D)100%

Unlock Deck
Unlock for access to all 39 flashcards in this deck.
Unlock Deck
k this deck
37
A very large gardening business grows rose bushes for sale to garden stores around the world. The most popular colors are red, pink, and white. The business decides on 50% red roses, 30% pink, and 20% white. A gardener orders 10 rose bushes selected randomly from a huge field. Her primary interest is in pink roses. A good model for the number of bushes with pink roses is:
A)the binomial distribution.
B)the Normal distribution.
C)the Normal approximation to the binomial.
D)None of the answer options is correct.
A)the binomial distribution.
B)the Normal distribution.
C)the Normal approximation to the binomial.
D)None of the answer options is correct.

Unlock Deck
Unlock for access to all 39 flashcards in this deck.
Unlock Deck
k this deck
38
A very large gardening business grows rose bushes for sale to garden stores around the world. The most popular colors are red, pink, and white. The business decides on 50% red roses, 30% pink, and 20% white. A gardener orders 10 rose bushes selected randomly from a huge field. Her primary interest is in pink roses. Assuming rose bushes are selected independently, we can use the binomial distribution for calculations. The probability of getting at least 3 pink rose bushes is:
A)0.5.
B)0.617.
C)0.348.
D)0.259.
A)0.5.
B)0.617.
C)0.348.
D)0.259.

Unlock Deck
Unlock for access to all 39 flashcards in this deck.
Unlock Deck
k this deck
39
Suppose we flip a coin 10 times. The probability that heads occurs exactly the same number of times as tails on the 10 flips is:
A)0.1667.
B)0.2461.
C)0.3125.
D)0.5.
A)0.1667.
B)0.2461.
C)0.3125.
D)0.5.

Unlock Deck
Unlock for access to all 39 flashcards in this deck.
Unlock Deck
k this deck


