Deck 10: Sampling Distributions
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/28
Play
Full screen (f)
Deck 10: Sampling Distributions
1
Consider the following to answer the question(s) below:
The owner of a small convenience store is trying to decide whether to discontinue selling magazines. He suspects that only 5% of the customers buy magazines and thinks that he might be able to sell something more profitable. Before making a final decision, he keeps track of the number of customers who buy magazines each day. On a typical day he has 280 customers in his store.
On a typical day, what would be the mean number of customers who buy magazines?
A) 280
B) 0
C) 266
D) 14
E) 25
The owner of a small convenience store is trying to decide whether to discontinue selling magazines. He suspects that only 5% of the customers buy magazines and thinks that he might be able to sell something more profitable. Before making a final decision, he keeps track of the number of customers who buy magazines each day. On a typical day he has 280 customers in his store.
On a typical day, what would be the mean number of customers who buy magazines?
A) 280
B) 0
C) 266
D) 14
E) 25
D
2
It is generally believed that electrical problems affect about 14% of new cars. An automobile mechanic conducts diagnostic tests on 128 new cars on the lot.
a. Describe the sampling distribution for the sample proportion by naming the model and telling its mean and standard deviation.
b. What is the probability that in this group over 18% of the new cars will be found to have electrical problems?
a. Describe the sampling distribution for the sample proportion by naming the model and telling its mean and standard deviation.
b. What is the probability that in this group over 18% of the new cars will be found to have electrical problems?
a. We can assume these cars are a representative sample of all new cars, and certainly less than 10% of them. We expect 14% × 128 = 17.92 successes (electrical problems) and 86% × 128 = 110.08 failures (no problems) so the sample is large enough to use the sampling model N(0.14, 0.031).
b. z =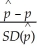 = 1.29, about 10%
= 1.29, about 10%
b. z =
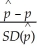 = 1.29, about 10%
= 1.29, about 10% 3
Consider the following to answer the question(s) below:
The owner of a small convenience store is trying to decide whether to discontinue selling magazines. He suspects that only 5% of the customers buy magazines and thinks that he might be able to sell something more profitable. Before making a final decision, he keeps track of the number of customers who buy magazines each day. On a typical day he has 280 customers in his store.
On a typical day, what would be the standard deviation in the number of customers who buy magazines?
A) 3.65
B) 14
C) 13.32
D) 25
E) 5
The owner of a small convenience store is trying to decide whether to discontinue selling magazines. He suspects that only 5% of the customers buy magazines and thinks that he might be able to sell something more profitable. Before making a final decision, he keeps track of the number of customers who buy magazines each day. On a typical day he has 280 customers in his store.
On a typical day, what would be the standard deviation in the number of customers who buy magazines?
A) 3.65
B) 14
C) 13.32
D) 25
E) 5
A
4
Consider the following to answer the question(s) below:
In a metal fabrication process, metal rods are produced that have an average length of 20.5 metres with a standard deviation of 2.3 metres. A quality control specialist collects a random sample of 30 rods and measures their lengths.
The sampling distribution of the sample mean lengths is Normally distributed with a mean of 20.5 metres and standard deviation of 0.42 metres. We can say this because
A) The sample size is not too large.
B) The Central Limit theorem applies.
C) The Normal Probability theorem applies.
D) All of the above
E) None of the above
In a metal fabrication process, metal rods are produced that have an average length of 20.5 metres with a standard deviation of 2.3 metres. A quality control specialist collects a random sample of 30 rods and measures their lengths.
The sampling distribution of the sample mean lengths is Normally distributed with a mean of 20.5 metres and standard deviation of 0.42 metres. We can say this because
A) The sample size is not too large.
B) The Central Limit theorem applies.
C) The Normal Probability theorem applies.
D) All of the above
E) None of the above

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
5
Suppose that the mean income of people in a region is $35,000 with a standard deviation of $6000. It is known that the population is unimodal and symmetric. For a sample of size 25,
a. Describe the sampling distribution for the sample.
b. What is the probability of obtaining from a sample of 25 people an average income that is above $37,000?
a. Describe the sampling distribution for the sample.
b. What is the probability of obtaining from a sample of 25 people an average income that is above $37,000?

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
6
Consider the following to answer the question(s) below:
According to a recent survey, about 33% of Canadians polled said that they would likely purchase reusable cloth bags for groceries in order to reduce plastic waste. Suppose 45 shoppers are interviewed at a local supermarket.
Which of the following statements is (are) true about the sampling distribution of the sample proportion?
A) The sampling distribution can be described by the Normal model.
B) The mean of the sampling distribution is 0.33.
C) The standard deviation of the sampling distribution is 0.07.
D) All of the above
E) None of the above
According to a recent survey, about 33% of Canadians polled said that they would likely purchase reusable cloth bags for groceries in order to reduce plastic waste. Suppose 45 shoppers are interviewed at a local supermarket.
Which of the following statements is (are) true about the sampling distribution of the sample proportion?
A) The sampling distribution can be described by the Normal model.
B) The mean of the sampling distribution is 0.33.
C) The standard deviation of the sampling distribution is 0.07.
D) All of the above
E) None of the above

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
7
What are the 2 assumptions and 3 conditions for the distribution of sample proportions? Explain these.

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
8
A company has determined that the mean number of days it takes to collect on its accounts receivable is 36, with a standard deviation of 11 days. The company plans to select a random sample of n = 12 accounts and compute the sample mean. Which of the following statements holds true in this situation?
A) The sampling distribution may actually be approximately Normally distributed depending on what the population distribution is.
B) The sampling distribution will always have the same distribution as the population.
C) The sampling variability will be greater than if they had sampled n = 64 accounts.
D) The sampling distribution will certainly be approximately Normally distributed in this case.
E) The sampling distribution cannot be approximately Normally distributed in this case.
A) The sampling distribution may actually be approximately Normally distributed depending on what the population distribution is.
B) The sampling distribution will always have the same distribution as the population.
C) The sampling variability will be greater than if they had sampled n = 64 accounts.
D) The sampling distribution will certainly be approximately Normally distributed in this case.
E) The sampling distribution cannot be approximately Normally distributed in this case.

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
9
Which of the following is not an assumption or condition for the CLT?
A) the independence assumption
B) the sample size assumption
C) the randomization condition
D) the 10% condition
E) the success/failure condition
A) the independence assumption
B) the sample size assumption
C) the randomization condition
D) the 10% condition
E) the success/failure condition

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
10
Consider the following to answer the question(s) below:
In a metal fabrication process, metal rods are produced that have an average length of 20.5 metres with a standard deviation of 2.3 metres. A quality control specialist collects a random sample of 30 rods and measures their lengths.
Suppose the resulting sample mean is 19.5 metres. Which of the following statements is true?
A) This sample mean is 2.38 standard deviations above what we expect.
B) This sample mean is more than 3 standard deviations away from the population mean.
C) This sample mean is 2.38 standard deviations below what we expect.
D) This sample mean is only 1 standard deviation above the population mean.
E) This sample mean is only 1 standard deviation below the population mean.
In a metal fabrication process, metal rods are produced that have an average length of 20.5 metres with a standard deviation of 2.3 metres. A quality control specialist collects a random sample of 30 rods and measures their lengths.
Suppose the resulting sample mean is 19.5 metres. Which of the following statements is true?
A) This sample mean is 2.38 standard deviations above what we expect.
B) This sample mean is more than 3 standard deviations away from the population mean.
C) This sample mean is 2.38 standard deviations below what we expect.
D) This sample mean is only 1 standard deviation above the population mean.
E) This sample mean is only 1 standard deviation below the population mean.

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
11
A small business ships specialty homemade candies to anywhere in the world. Past records indicate that orders weigh an average of 118 grams with a standard deviation of 14 grams. Suppose a random sample of 50 current orders is selected and each weighed.
a. Describe the sampling distribution of the sample mean by naming the model and telling its mean and standard deviation.
b. Suppose the resulting sample mean is 110 grams. Do you think that this sample result is unusually small? Explain.
a. Describe the sampling distribution of the sample mean by naming the model and telling its mean and standard deviation.
b. Suppose the resulting sample mean is 110 grams. Do you think that this sample result is unusually small? Explain.

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
12
What are the 2 assumptions and 3 conditions of the Central Limit Theorem? Explain these.

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
13
Suppose that in a recent survey, about 33% of Canadians polled said that they would likely purchase reusable cloth bags for groceries in order to reduce plastic waste. Suppose 45 shoppers are interviewed a local supermarket.
a. Describe the sampling distribution of the sample proportion by naming the model and telling its mean and standard deviation.
b. What is the probability that no more than 12 shoppers will say that they are likely to purchase reusable cloth bags for groceries?
a. Describe the sampling distribution of the sample proportion by naming the model and telling its mean and standard deviation.
b. What is the probability that no more than 12 shoppers will say that they are likely to purchase reusable cloth bags for groceries?

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
14
It is believed that 40% of all medical doctors in Canada are women. Suppose that a random sample of 100 doctors is selected. Find the probability that at least 50% of this sample will be women.
A) 50%
B) 47.93%
C) 2.07%
D) 52.07%
E) 97.93%
A) 50%
B) 47.93%
C) 2.07%
D) 52.07%
E) 97.93%

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
15
Suppose it is known that the income distribution in a particular region is right-skewed and bimodal. If bank economists are interested in estimating the mean income, which of the following is true?
A) Provided that the sample size is sufficiently large, the sampling distribution for y will be approximately Normal with a mean equal to the population mean.
B) Provided that the sample size is sufficiently large, the sampling distribution for y will be approximately Normal with a standard deviation equal to the population standard deviation.
C) The sampling distribution will also be right-skewed for large sample sizes.
D) The standard deviation of the sampling distribution for y will be proportionally larger than the population standard deviation, depending on the size of the sample.
E) The sampling distribution will also be bimodal for large sample sizes.
A) Provided that the sample size is sufficiently large, the sampling distribution for y will be approximately Normal with a mean equal to the population mean.
B) Provided that the sample size is sufficiently large, the sampling distribution for y will be approximately Normal with a standard deviation equal to the population standard deviation.
C) The sampling distribution will also be right-skewed for large sample sizes.
D) The standard deviation of the sampling distribution for y will be proportionally larger than the population standard deviation, depending on the size of the sample.
E) The sampling distribution will also be bimodal for large sample sizes.

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
16
Consider the following to answer the question(s) below:
According to a recent survey, about 33% of Canadians polled said that they would likely purchase reusable cloth bags for groceries in order to reduce plastic waste. Suppose 45 shoppers are interviewed at a local supermarket.
What is the probability that no more than 12 shoppers will say that they are likely to purchase reusable cloth bags for groceries?
A) -0.90
B) 0.90
C) 0.267
D) 0.816
E) 0.184
According to a recent survey, about 33% of Canadians polled said that they would likely purchase reusable cloth bags for groceries in order to reduce plastic waste. Suppose 45 shoppers are interviewed at a local supermarket.
What is the probability that no more than 12 shoppers will say that they are likely to purchase reusable cloth bags for groceries?
A) -0.90
B) 0.90
C) 0.267
D) 0.816
E) 0.184

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
17
Suppose that it is believed that 40% of adults have a company pension. If 100 adults are surveyed,
a. What is the probability of finding a sample with less than 30 adults having a company pension?
b. What is the probability of finding no more than 45 adults having a company pension?
a. What is the probability of finding a sample with less than 30 adults having a company pension?
b. What is the probability of finding no more than 45 adults having a company pension?

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
18
In a metal fabrication process, metal rods are produced that have an average length of 20.5 metres with a standard deviation of 2.3 metres. A quality control specialist collects a random sample of 30 rods and measures their lengths.
a. Describe the sampling distribution for the sample mean by naming the model and telling its mean and standard deviation.
b. Suppose the resulting sample mean is 19.5 metres. Do you think that this sample result is unusually small? Explain.
a. Describe the sampling distribution for the sample mean by naming the model and telling its mean and standard deviation.
b. Suppose the resulting sample mean is 19.5 metres. Do you think that this sample result is unusually small? Explain.

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
19
It is believed that on average, households spend $150 a week on groceries with a standard deviation of $50. What is the probability that in a sample of 64 households, the average amount spent on groceries will be no more than $140 per week?
A) 44.52%
B) 5.48%
C) 55.48%
D) 94.52%
E) 19.15%
A) 44.52%
B) 5.48%
C) 55.48%
D) 94.52%
E) 19.15%

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
20
Which of the following is not an assumption or condition for the distribution of sample proportions?
A) the independence assumption
B) the sample size assumption
C) the randomization condition
D) the 10% condition
E) the large enough sample condition
A) the independence assumption
B) the sample size assumption
C) the randomization condition
D) the 10% condition
E) the large enough sample condition

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
21
According to the local real estate board, the average number of days that homes stay on the market before selling is 78.4, with a standard deviation equal to 11 days. A prospective seller selected a random sample of 36 homes from the multiple listing service. Above what value for the sample mean should 95 percent of all possible sample means fall?
A) about 75.4 days
B) about 81.4 days
C) about 96.5 days
D) about 60.3 days
E) about 79.3 days
A) about 75.4 days
B) about 81.4 days
C) about 96.5 days
D) about 60.3 days
E) about 79.3 days

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
22
Ian's Tree Farm grows spruce trees for nurseries. The average annual increase in tree diameter is 7.9 centimetres with a standard deviation of 1.3 centimetres. A random sample of n = 50 trees is collected. What is the probability of the sample mean being less the 7.4 centimetres?
A) 0.0033
B) 0.4977
C) 0.5023
D) 0.9977
E) 0.9954
A) 0.0033
B) 0.4977
C) 0.5023
D) 0.9977
E) 0.9954

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
23
A major textbook publisher has a contract with a printing company. Part of the contract stipulates that no more than 5 percent of the pages should have any type of printing error. Suppose that the company selects a random sample of 400 pages and finds 33 that have an error. If the printer is meeting the standard, what is the probability that a sample this size would have 33 or more errors?
A) 0.0014
B) 0.4986
C) 0.9986
D) 0.1245
E) 0.3755
A) 0.0014
B) 0.4986
C) 0.9986
D) 0.1245
E) 0.3755

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
24
A golf course in Toronto has determined that the mean time it takes for a foursome to complete an 18-hole round of golf is 4 hours 35 minutes (275 minutes) with a standard deviation of 14 minutes. The time distribution is also thought to be approximately Normal. Every month, the head pro at the course randomly selects a sample of 8 foursomes and monitors the time it takes them to play. Suppose the mean time that was observed for the sample last month was 4 hours 44 minutes (284 minutes). What is the probability of seeing a sample mean this high or higher?
A) about 0.0344
B) about 0.4656
C) about 0.9656
D) about 0.2611
E) about 0.2389
A) about 0.0344
B) about 0.4656
C) about 0.9656
D) about 0.2611
E) about 0.2389

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
25
Which of the following statements is consistent with the Central Limit Theorem?
A) The Central Limit Theorem indicates that the sampling distribution will be approximately Normal when the sample size is sufficiently large.
B) The Central Limit Theorem applies without regard to the size of the sample.
C) The Central Limit Theorem applies to both dependent and independent sampled values regardless of sample size.
D) The Central Limit Theorem makes sense even if samples are not randomly selected.
E) The Central Limit Theorem applies only to populations with Normal distributions.
A) The Central Limit Theorem indicates that the sampling distribution will be approximately Normal when the sample size is sufficiently large.
B) The Central Limit Theorem applies without regard to the size of the sample.
C) The Central Limit Theorem applies to both dependent and independent sampled values regardless of sample size.
D) The Central Limit Theorem makes sense even if samples are not randomly selected.
E) The Central Limit Theorem applies only to populations with Normal distributions.

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
26
McCain Foods (Canada) of New Brunswick produces frozen French fries. Suppose one line of fries has an average length of 7.62 centimetres with a standard deviation of 1.27 centimetres. To make sure that the quality standard is met, they plan to select a random sample of n = 100 fries each day. Yesterday, the sample mean was 7.75 centimetres. What is the probability that the mean would be 7.75 centimetres or more if they are meeting the quality standards?
A) 0.1539
B) 0.3413
C) 0.6587
D) 0.0398
E) 0.4602
A) 0.1539
B) 0.3413
C) 0.6587
D) 0.0398
E) 0.4602

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
27
A claim was recently made on national television that two of every three doctors recommend a particular pain killer. Suppose a random sample of n = 300 doctors revealed that 180 said that they would recommend the painkiller. If the TV claim is correct, what is the probability of 180 or fewer in the sample agreeing?
A) 0.0071
B) 0.4929
C) 0.9929
D) 0.0142
E) 0.5071
A) 0.0071
B) 0.4929
C) 0.9929
D) 0.0142
E) 0.5071

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
28
Which of the following statements is true with respect to the sampling distribution of a proportion?
A) The mean of the sampling distribution will equal the population proportion.
B) An increase in the sample size will result in an increase in the size of the standard deviation.
C) The sampling distribution will be approximately Normal regardless of sample size.
D) The standard deviation of the sampling distribution will equal the standard deviation of the population.
E) The mean of the sampling distribution will smaller than the population proportion.
A) The mean of the sampling distribution will equal the population proportion.
B) An increase in the sample size will result in an increase in the size of the standard deviation.
C) The sampling distribution will be approximately Normal regardless of sample size.
D) The standard deviation of the sampling distribution will equal the standard deviation of the population.
E) The mean of the sampling distribution will smaller than the population proportion.

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck


