Deck 9: Section 7: Infinite Series
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/18
Play
Full screen (f)
Deck 9: Section 7: Infinite Series
1
Find the Maclaurin polynomial of degree 3 for the function. 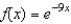
A)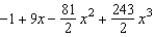
B)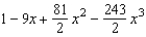
C)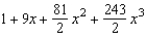
D)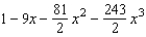
E)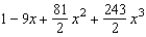
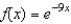
A)
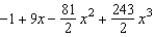
B)
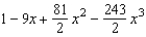
C)
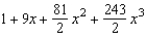
D)
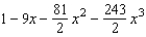
E)
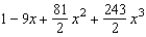
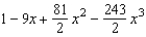
2
Determine the values of x for which the function 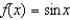 can be replaced by the Taylor polynomial
can be replaced by the Taylor polynomial 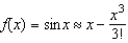 if the error cannot exceed 0.008. Round your answer to four decimal places.
if the error cannot exceed 0.008. Round your answer to four decimal places.
A)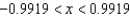
B)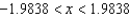
C)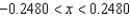
D)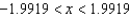
E)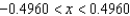
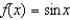 can be replaced by the Taylor polynomial
can be replaced by the Taylor polynomial 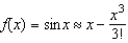 if the error cannot exceed 0.008. Round your answer to four decimal places.
if the error cannot exceed 0.008. Round your answer to four decimal places.A)
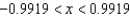
B)
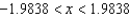
C)
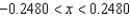
D)
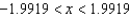
E)
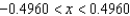
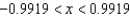
3
Find a first-degree polynomial function P1 whose value and slope agree with the value and slope of f at 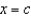 . What is P1 called?
. What is P1 called? 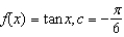
A)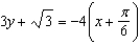 ; tangent line to
; tangent line to 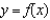 at
at 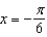
B)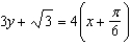 ; secant line to
; secant line to 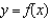 at
at 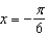
C)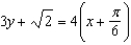 ; tangent line to
; tangent line to 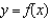 at
at 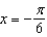
D)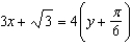 ; differential of
; differential of 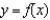 at
at 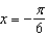
E)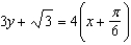 ; tangent line to
; tangent line to 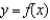 at
at 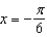
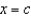 . What is P1 called?
. What is P1 called? 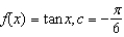
A)
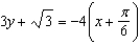 ; tangent line to
; tangent line to 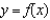 at
at 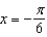
B)
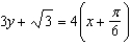 ; secant line to
; secant line to 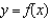 at
at 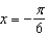
C)
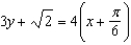 ; tangent line to
; tangent line to 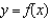 at
at 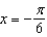
D)
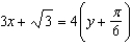 ; differential of
; differential of 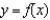 at
at 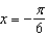
E)
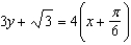 ; tangent line to
; tangent line to 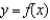 at
at 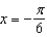
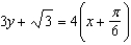 ; tangent line to
; tangent line to 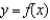 at
at 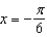
4
Find the Maclaurin polynomial of degree 4 for the function. 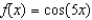
A)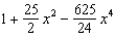
B)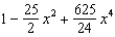
C)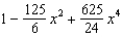
D)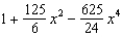
E)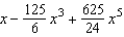
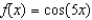
A)
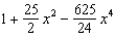
B)
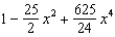
C)
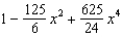
D)
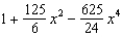
E)
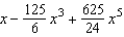

Unlock Deck
Unlock for access to all 18 flashcards in this deck.
Unlock Deck
k this deck
5
Find the Maclaurin polynomial of degree two for the function 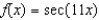 .
.
A)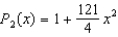
B)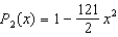
C)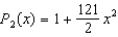
D)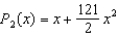
E)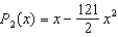
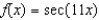 .
.A)
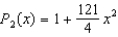
B)
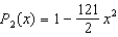
C)
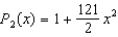
D)
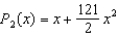
E)
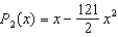

Unlock Deck
Unlock for access to all 18 flashcards in this deck.
Unlock Deck
k this deck
6
Consider the function 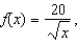 and its second-degree polynomial
and its second-degree polynomial 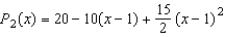 at
at 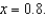 Compute the value of
Compute the value of 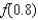 and
and 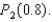 Round your answer to four decimal places.
Round your answer to four decimal places.
A)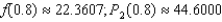
B)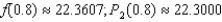
C)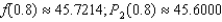
D)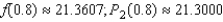
E)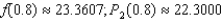
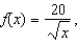 and its second-degree polynomial
and its second-degree polynomial 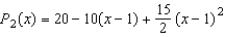 at
at 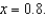 Compute the value of
Compute the value of 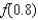 and
and 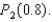 Round your answer to four decimal places.
Round your answer to four decimal places.A)
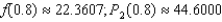
B)
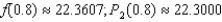
C)
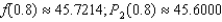
D)
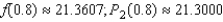
E)
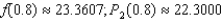

Unlock Deck
Unlock for access to all 18 flashcards in this deck.
Unlock Deck
k this deck
7
Find the fourth degree Maclaurin polynomial for the function. 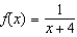
A)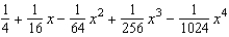
B)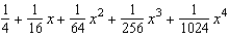
C)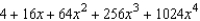
D)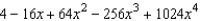
E)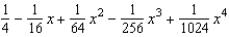
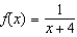
A)
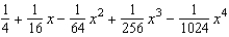
B)
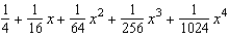
C)
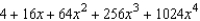
D)
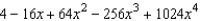
E)
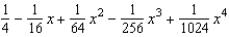

Unlock Deck
Unlock for access to all 18 flashcards in this deck.
Unlock Deck
k this deck
8
Find the third degree Taylor polynomial centered at 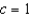 for the function.
for the function. 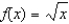
A)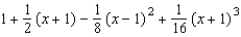
B)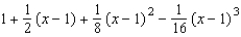
C)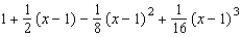
D)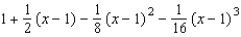
E)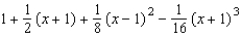
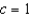 for the function.
for the function. 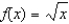
A)
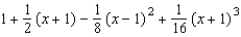
B)
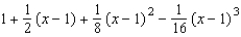
C)
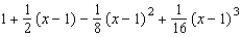
D)
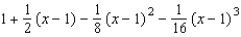
E)
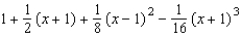

Unlock Deck
Unlock for access to all 18 flashcards in this deck.
Unlock Deck
k this deck
9
Find the third Taylor polynomial for 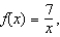 expanded about
expanded about 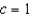 .
.
A)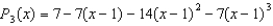
B)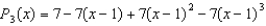
C)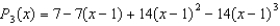
D)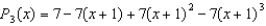
E)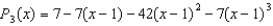
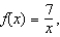 expanded about
expanded about 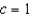 .
.A)
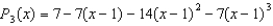
B)
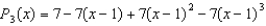
C)
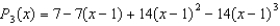
D)
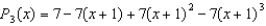
E)
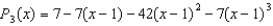

Unlock Deck
Unlock for access to all 18 flashcards in this deck.
Unlock Deck
k this deck
10
The fourth Taylor polynomial for 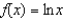 , expanded about
, expanded about 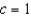 is
is 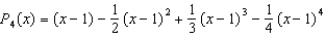 . Use this polynomial to approximate the value of
. Use this polynomial to approximate the value of 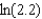 . Round your answer to four decimal places.
. Round your answer to four decimal places.
A) 2.9184
B) 2.6976
C) 3.0144
D) 0.5664
E) 0.5376
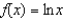 , expanded about
, expanded about 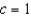 is
is 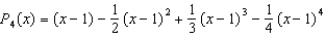 . Use this polynomial to approximate the value of
. Use this polynomial to approximate the value of 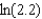 . Round your answer to four decimal places.
. Round your answer to four decimal places.A) 2.9184
B) 2.6976
C) 3.0144
D) 0.5664
E) 0.5376

Unlock Deck
Unlock for access to all 18 flashcards in this deck.
Unlock Deck
k this deck
11
Find a first-degree polynomial function P1 whose value and slope agree with the value and slope of f at 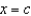 . What is P1 called?
. What is P1 called? 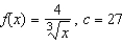
A)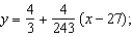 tangent line to
tangent line to 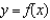 at
at 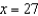
B)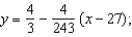 secant line to
secant line to 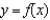 at
at 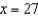
C)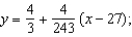 secant line to
secant line to 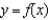 at
at 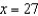
D)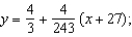 secant line to
secant line to 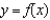 at
at 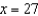
E)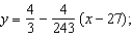 tangent line to
tangent line to 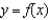 at
at 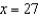
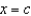 . What is P1 called?
. What is P1 called? 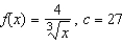
A)
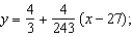 tangent line to
tangent line to 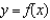 at
at 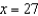
B)
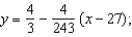 secant line to
secant line to 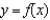 at
at 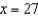
C)
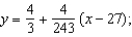 secant line to
secant line to 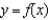 at
at 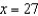
D)
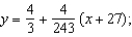 secant line to
secant line to 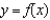 at
at 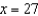
E)
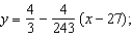 tangent line to
tangent line to 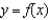 at
at 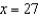

Unlock Deck
Unlock for access to all 18 flashcards in this deck.
Unlock Deck
k this deck
12
What is 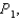 a first-degree polynomial function whose value and slope agree with the value and slope of
a first-degree polynomial function whose value and slope agree with the value and slope of 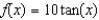 at
at 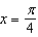 ?
?
A) is the tangent line to the curve
is the tangent line to the curve 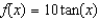 at the point
at the point 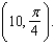
B)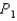 is the tangent line to the curve
is the tangent line to the curve 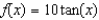 at the point
at the point 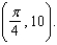
C)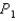 is the tangent line to the curve
is the tangent line to the curve 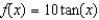 at the point
at the point 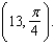
D)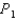 is the tangent line to the curve
is the tangent line to the curve 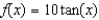 at the point
at the point 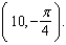
E)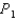 is the tangent line to the curve
is the tangent line to the curve 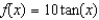 at the point
at the point 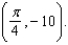
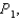 a first-degree polynomial function whose value and slope agree with the value and slope of
a first-degree polynomial function whose value and slope agree with the value and slope of 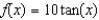 at
at 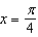 ?
?A)
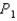 is the tangent line to the curve
is the tangent line to the curve 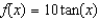 at the point
at the point 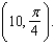
B)
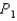 is the tangent line to the curve
is the tangent line to the curve 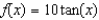 at the point
at the point 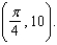
C)
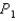 is the tangent line to the curve
is the tangent line to the curve 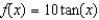 at the point
at the point 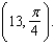
D)
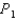 is the tangent line to the curve
is the tangent line to the curve 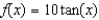 at the point
at the point 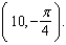
E)
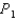 is the tangent line to the curve
is the tangent line to the curve 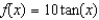 at the point
at the point 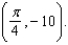

Unlock Deck
Unlock for access to all 18 flashcards in this deck.
Unlock Deck
k this deck
13
Determine the degree of the Maclaurin polynomial required for the error in the approximation of the function 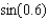 to be less than 0.001.
to be less than 0.001.
A)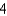
B) 2
C) 5
D) 1
E) 3
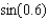 to be less than 0.001.
to be less than 0.001.A)
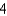
B) 2
C) 5
D) 1
E) 3

Unlock Deck
Unlock for access to all 18 flashcards in this deck.
Unlock Deck
k this deck
14
Find the Maclaurin polynomial of degree 5 for the function. 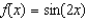
A)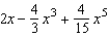
B)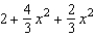
C)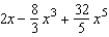
D)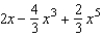
E)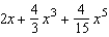
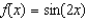
A)
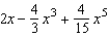
B)
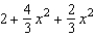
C)
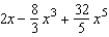
D)
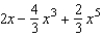
E)
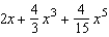

Unlock Deck
Unlock for access to all 18 flashcards in this deck.
Unlock Deck
k this deck
15
Find the Maclaurin polynomial of degree 4 for the function. 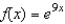
A)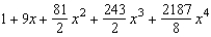
B)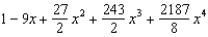
C)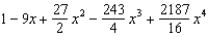
D)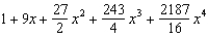
E)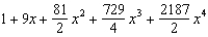
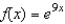
A)
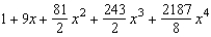
B)
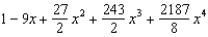
C)
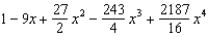
D)
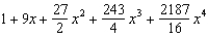
E)
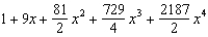

Unlock Deck
Unlock for access to all 18 flashcards in this deck.
Unlock Deck
k this deck
16
Find a first-degree polynomial function P1 whose value and slope agree with the value and slope of 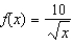 at
at 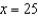 .
.
A)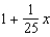
B)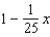
C)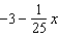
D)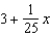
E)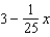
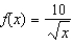 at
at 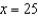 .
.A)
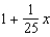
B)
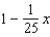
C)
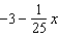
D)
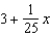
E)
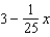

Unlock Deck
Unlock for access to all 18 flashcards in this deck.
Unlock Deck
k this deck
17
Find the fourth degree Taylor polynomial centered at 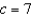 for the function.
for the function. 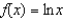
A)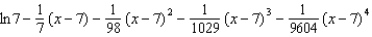
B)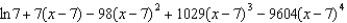
C)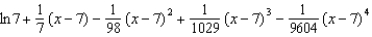
D)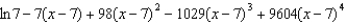
E)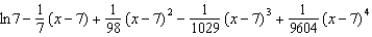
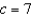 for the function.
for the function. 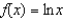
A)
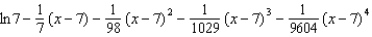
B)
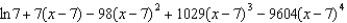
C)
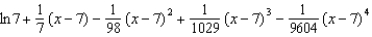
D)
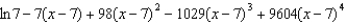
E)
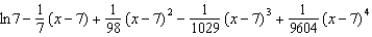

Unlock Deck
Unlock for access to all 18 flashcards in this deck.
Unlock Deck
k this deck
18
Use a graphing utility to graph 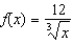 and P1, a first-degree polynomial function whose value and slope agree with the value and slope of f at
and P1, a first-degree polynomial function whose value and slope agree with the value and slope of f at 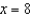 .
.
A)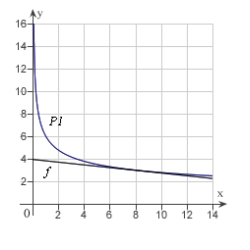
B)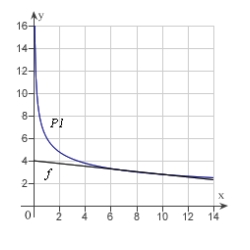
C)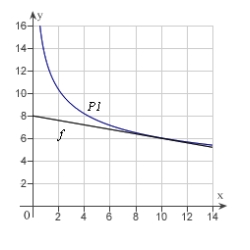
D)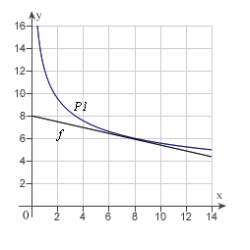
E)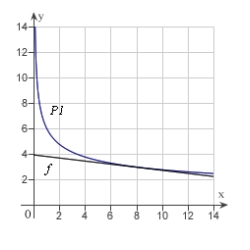
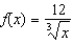 and P1, a first-degree polynomial function whose value and slope agree with the value and slope of f at
and P1, a first-degree polynomial function whose value and slope agree with the value and slope of f at 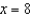 .
.A)

B)

C)

D)

E)


Unlock Deck
Unlock for access to all 18 flashcards in this deck.
Unlock Deck
k this deck


