Deck 9: Section 5: Infinite Series
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/15
Play
Full screen (f)
Deck 9: Section 5: Infinite Series
1
The series 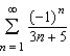 is a convergent series. Use Theorem 9.15 to determine the number of terms required to approximate the sum of this series with an error less than 0.001.
is a convergent series. Use Theorem 9.15 to determine the number of terms required to approximate the sum of this series with an error less than 0.001.
A)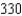
B)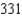
C)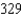
D)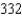
E)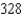
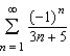 is a convergent series. Use Theorem 9.15 to determine the number of terms required to approximate the sum of this series with an error less than 0.001.
is a convergent series. Use Theorem 9.15 to determine the number of terms required to approximate the sum of this series with an error less than 0.001.A)
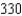
B)
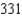
C)
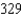
D)
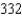
E)
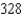
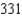
2
Use the Alternating Series Test (if possible) to determine whether the series 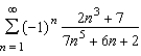 converges or diverges?
converges or diverges?
A)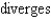
B)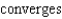
C) Alternating Series Test cannot be applied
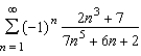 converges or diverges?
converges or diverges?A)
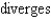
B)
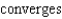
C) Alternating Series Test cannot be applied
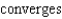
3
Determine whether the series 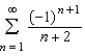 converges conditionally or absolutely, or diverges.
converges conditionally or absolutely, or diverges.
A) The series converges conditionally but does not converge absolutely.
B) The series converges absolutely but does not converge conditionally.
C) The series diverges.
D) The series converges absolutely.
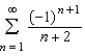 converges conditionally or absolutely, or diverges.
converges conditionally or absolutely, or diverges.A) The series converges conditionally but does not converge absolutely.
B) The series converges absolutely but does not converge conditionally.
C) The series diverges.
D) The series converges absolutely.
The series converges conditionally but does not converge absolutely.
4
Consider the series 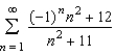 . Review the Alternating Series Test to determine which of the following statements is true for the given series.
. Review the Alternating Series Test to determine which of the following statements is true for the given series.
A) Since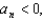 for some n, the series diverges.
for some n, the series diverges.
B) Since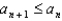 cannot be shown to be true for all n, the Alternating Series Test cannot be applied.
cannot be shown to be true for all n, the Alternating Series Test cannot be applied.
C) The series converges.
D) Since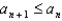 cannot be shown to be true for all n, the series diverges.
cannot be shown to be true for all n, the series diverges.
E) Since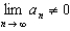 , the series diverges.
, the series diverges.
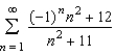 . Review the Alternating Series Test to determine which of the following statements is true for the given series.
. Review the Alternating Series Test to determine which of the following statements is true for the given series.A) Since
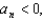 for some n, the series diverges.
for some n, the series diverges.B) Since
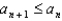 cannot be shown to be true for all n, the Alternating Series Test cannot be applied.
cannot be shown to be true for all n, the Alternating Series Test cannot be applied.C) The series converges.
D) Since
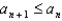 cannot be shown to be true for all n, the series diverges.
cannot be shown to be true for all n, the series diverges.E) Since
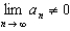 , the series diverges.
, the series diverges.
Unlock Deck
Unlock for access to all 15 flashcards in this deck.
Unlock Deck
k this deck
5
Determine whether the series 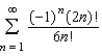 converges absolutely, converges conditionally, or diverges.
converges absolutely, converges conditionally, or diverges.
A) converges absolutely
B) diverges
C) converges conditionally
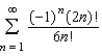 converges absolutely, converges conditionally, or diverges.
converges absolutely, converges conditionally, or diverges.A) converges absolutely
B) diverges
C) converges conditionally

Unlock Deck
Unlock for access to all 15 flashcards in this deck.
Unlock Deck
k this deck
6
Consider the series 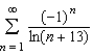 . Review the Alternating Series Test to determine which of the following statements is true for the given series.
. Review the Alternating Series Test to determine which of the following statements is true for the given series.
A) Since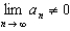 , the series diverges.
, the series diverges.
B) Since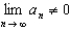 , the Alternating Series Test cannot be applied.
, the Alternating Series Test cannot be applied.
C) Since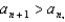 for some n, the Alternating Series Test cannot be applied.
for some n, the Alternating Series Test cannot be applied.
D) Since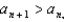 for some n, the series diverges.
for some n, the series diverges.
E) The series converges.
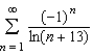 . Review the Alternating Series Test to determine which of the following statements is true for the given series.
. Review the Alternating Series Test to determine which of the following statements is true for the given series.A) Since
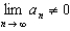 , the series diverges.
, the series diverges.B) Since
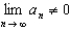 , the Alternating Series Test cannot be applied.
, the Alternating Series Test cannot be applied.C) Since
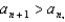 for some n, the Alternating Series Test cannot be applied.
for some n, the Alternating Series Test cannot be applied.D) Since
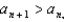 for some n, the series diverges.
for some n, the series diverges.E) The series converges.

Unlock Deck
Unlock for access to all 15 flashcards in this deck.
Unlock Deck
k this deck
7
It can be shown that 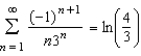 According to Theorem 9.15, the partial sum
According to Theorem 9.15, the partial sum 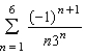 approximates
approximates 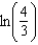 with error less than how much?
with error less than how much?
A)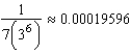
B)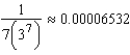
C)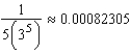
D)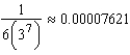
E)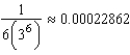
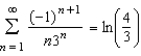 According to Theorem 9.15, the partial sum
According to Theorem 9.15, the partial sum 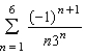 approximates
approximates 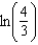 with error less than how much?
with error less than how much?A)
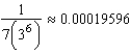
B)
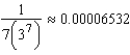
C)
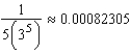
D)
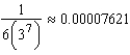
E)
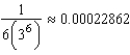

Unlock Deck
Unlock for access to all 15 flashcards in this deck.
Unlock Deck
k this deck
8
True or false: The series 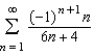 converges.
converges.
A)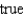
B)
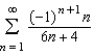 converges.
converges.A)
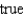
B)


Unlock Deck
Unlock for access to all 15 flashcards in this deck.
Unlock Deck
k this deck
9
True or false: The series 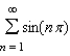 diverges.
diverges.
A)
B)
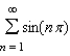 diverges.
diverges.A)

B)

Unlock Deck
Unlock for access to all 15 flashcards in this deck.
Unlock Deck
k this deck
10
Determine whether the series 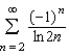 converges conditionally or absolutely, or diverges.
converges conditionally or absolutely, or diverges.
A) The series converges absolutely.
B) The series diverges.
C) The series converges absolutely but does not converge conditionally.
D) The series converges conditionally but does not converge absolutely.
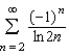 converges conditionally or absolutely, or diverges.
converges conditionally or absolutely, or diverges.A) The series converges absolutely.
B) The series diverges.
C) The series converges absolutely but does not converge conditionally.
D) The series converges conditionally but does not converge absolutely.

Unlock Deck
Unlock for access to all 15 flashcards in this deck.
Unlock Deck
k this deck
11
True or false: The series 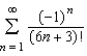 converges .
converges .
A)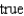
B)
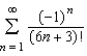 converges .
converges .A)
B)


Unlock Deck
Unlock for access to all 15 flashcards in this deck.
Unlock Deck
k this deck
12
Determine whether the series 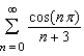 converges conditionally or absolutely, or diverges.
converges conditionally or absolutely, or diverges.
A) The series converges absolutely.
B) The series diverges.
C) The series converges absolutely but does not converge conditionally.
D) The series converges conditionally but does not converge absolutely.
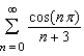 converges conditionally or absolutely, or diverges.
converges conditionally or absolutely, or diverges.A) The series converges absolutely.
B) The series diverges.
C) The series converges absolutely but does not converge conditionally.
D) The series converges conditionally but does not converge absolutely.

Unlock Deck
Unlock for access to all 15 flashcards in this deck.
Unlock Deck
k this deck
13
Determine whether the series 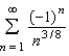 converges absolutely, converges conditionally, or diverges.
converges absolutely, converges conditionally, or diverges.
A)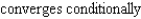
B) diverges
C)
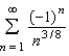 converges absolutely, converges conditionally, or diverges.
converges absolutely, converges conditionally, or diverges.A)
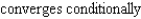
B) diverges
C)


Unlock Deck
Unlock for access to all 15 flashcards in this deck.
Unlock Deck
k this deck
14
Determine whether the series 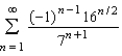 converges absolutely, converges conditionally, or diverges.
converges absolutely, converges conditionally, or diverges.
A)
B) converges conditionally
C)
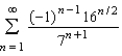 converges absolutely, converges conditionally, or diverges.
converges absolutely, converges conditionally, or diverges.A)

B) converges conditionally
C)

Unlock Deck
Unlock for access to all 15 flashcards in this deck.
Unlock Deck
k this deck
15
True or false: The series 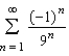 diverges.
diverges.
A)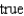
B)
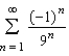 diverges.
diverges.A)
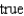
B)


Unlock Deck
Unlock for access to all 15 flashcards in this deck.
Unlock Deck
k this deck


