Deck 9: Section 2: Infinite Series
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/23
Play
Full screen (f)
Deck 9: Section 2: Infinite Series
1
True or false. The infinite series 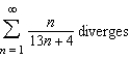 .
.
A) false
B) true
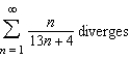 .
.A) false
B) true
true
2
Write the first five terms of the sequence of partial sums. 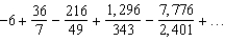
A)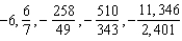
B)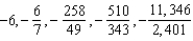
C)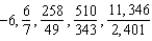
D)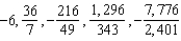
E)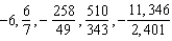
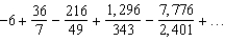
A)
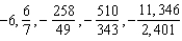
B)
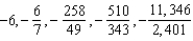
C)
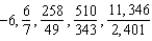
D)
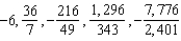
E)
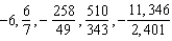
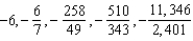
3
Write the repeating decimal 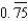 as a geometric series.
as a geometric series.
A)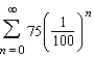
B)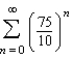
C)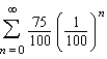
D)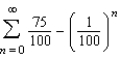
E)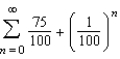
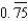 as a geometric series.
as a geometric series.A)
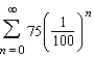
B)
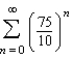
C)
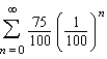
D)
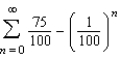
E)
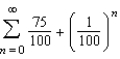
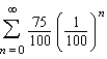
4
Determine the convergence or divergence of the series. 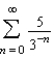
A) cannot be determined from the methods in the chapter
B) Diverges
C) Converges
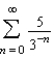
A) cannot be determined from the methods in the chapter
B) Diverges
C) Converges

Unlock Deck
Unlock for access to all 23 flashcards in this deck.
Unlock Deck
k this deck
5
Match the series with the graph of its sequence of partial sums. 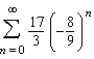
A)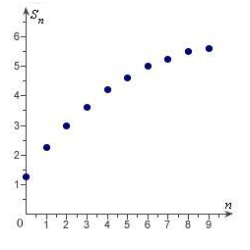
B)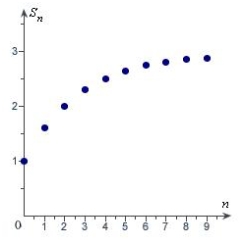
C)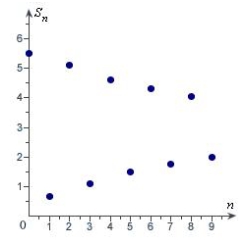
D)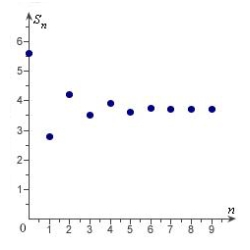
E)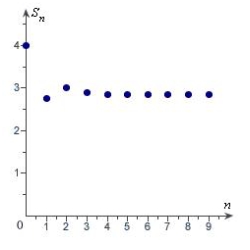
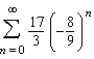
A)

B)

C)

D)

E)


Unlock Deck
Unlock for access to all 23 flashcards in this deck.
Unlock Deck
k this deck
6
Match the series with the graph of its sequence of partial sums. 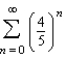
A)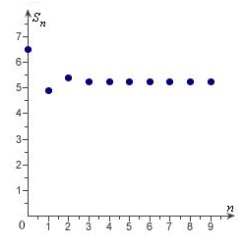
B)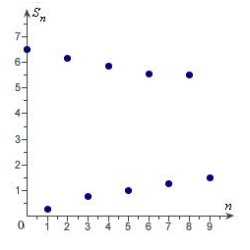
C)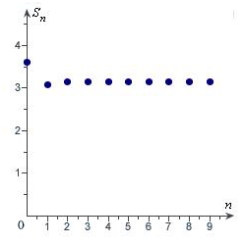
D)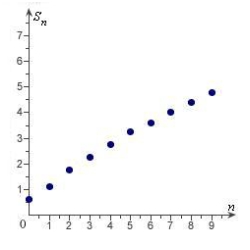
E)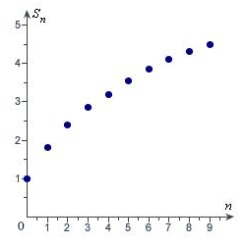
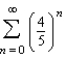
A)

B)

C)

D)

E)


Unlock Deck
Unlock for access to all 23 flashcards in this deck.
Unlock Deck
k this deck
7
Write the first five terms of the sequence of partial sums. 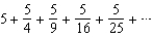
A)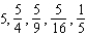
B)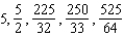
C)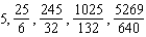
D)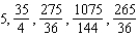
E)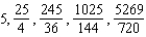
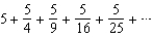
A)
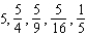
B)
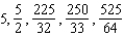
C)
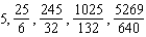
D)
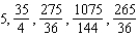
E)
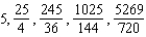

Unlock Deck
Unlock for access to all 23 flashcards in this deck.
Unlock Deck
k this deck
8
True or false. The series 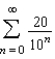 is divergent.
is divergent.
A) false
B) true
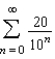 is divergent.
is divergent.A) false
B) true

Unlock Deck
Unlock for access to all 23 flashcards in this deck.
Unlock Deck
k this deck
9
Find the sum of the convergent series. 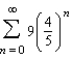
A) 4
B) 36
C) 9
D) 27
E) 45
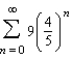
A) 4
B) 36
C) 9
D) 27
E) 45

Unlock Deck
Unlock for access to all 23 flashcards in this deck.
Unlock Deck
k this deck
10
Match the series with the graph of its sequence of partial sums. 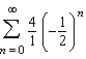
A)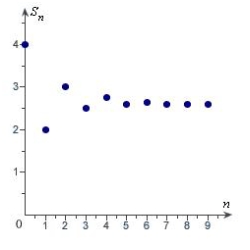
B)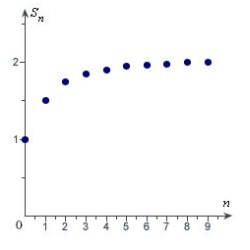
C)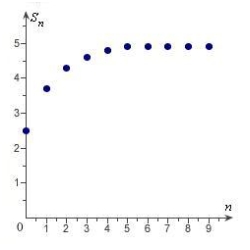
D)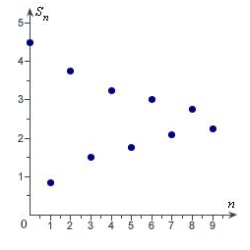
E)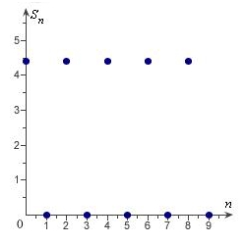
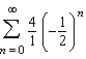
A)

B)

C)

D)

E)


Unlock Deck
Unlock for access to all 23 flashcards in this deck.
Unlock Deck
k this deck
11
Suppose an electronic games manufacturer producing a new product estimates the annual sales to be 4,000 units. Each year 20% of the units that have been sold will become inoperative. So, 4,000 units will be in use after 1 year, 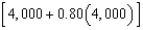 units will be in use after 2 years, and so on. How many units will be in use after n years?
units will be in use after 2 years, and so on. How many units will be in use after n years?
A)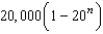 units
units
B)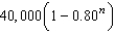 units
units
C)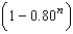 units
units
D)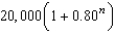 units
units
E)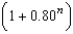 units
units
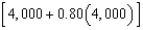 units will be in use after 2 years, and so on. How many units will be in use after n years?
units will be in use after 2 years, and so on. How many units will be in use after n years?A)
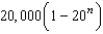 units
unitsB)
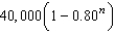 units
unitsC)
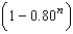 units
unitsD)
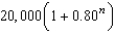 units
unitsE)
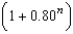 units
units
Unlock Deck
Unlock for access to all 23 flashcards in this deck.
Unlock Deck
k this deck
12
Find all values of x for which the series 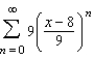 converges.
converges.
A)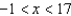
B)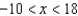
C)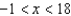
D)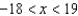
E)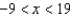
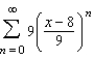 converges.
converges.A)
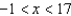
B)
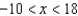
C)
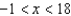
D)
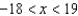
E)
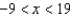

Unlock Deck
Unlock for access to all 23 flashcards in this deck.
Unlock Deck
k this deck
13
Suppose the annual spending by tourists in a resort city is $100 million. Approximately 75% of that revenue is again spent in the resort city, and of that amount approximately 75% is again spent in the same city, and so on. Summing all of this spending indefinitely, leads to the geometric series 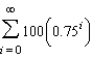 . Find the sum of this series.
. Find the sum of this series.
A) $800 million
B) $401 million
C) $200 million
D) $801 million
E) $400 million
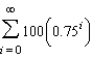 . Find the sum of this series.
. Find the sum of this series.A) $800 million
B) $401 million
C) $200 million
D) $801 million
E) $400 million

Unlock Deck
Unlock for access to all 23 flashcards in this deck.
Unlock Deck
k this deck
14
Find the sum of the convergent series 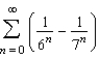 .
.
A)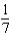
B)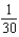
C)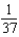
D)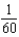
E)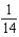
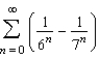 .
.A)
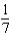
B)
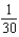
C)
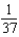
D)
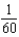
E)
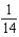

Unlock Deck
Unlock for access to all 23 flashcards in this deck.
Unlock Deck
k this deck
15
True or false. The series 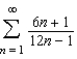 is convergent.
is convergent.
A) false
B) true
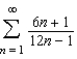 is convergent.
is convergent.A) false
B) true

Unlock Deck
Unlock for access to all 23 flashcards in this deck.
Unlock Deck
k this deck
16
Find the sum of the convergent series 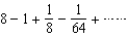
A)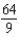
B)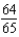
C)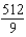
D)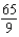
E)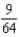
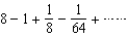
A)
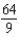
B)
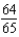
C)
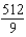
D)
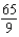
E)
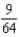

Unlock Deck
Unlock for access to all 23 flashcards in this deck.
Unlock Deck
k this deck
17
Write the first five terms of the sequence of partial sums. 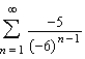
A)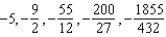
B)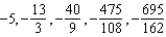
C)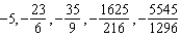
D)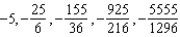
E)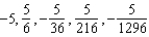
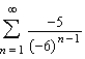
A)
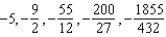
B)
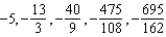
C)
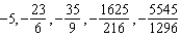
D)
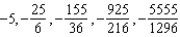
E)
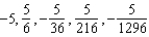

Unlock Deck
Unlock for access to all 23 flashcards in this deck.
Unlock Deck
k this deck
18
Find the sum of the convergent series. 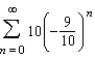
A)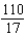
B)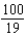
C)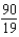
D)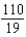
E)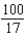
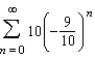
A)
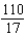
B)
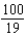
C)
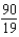
D)
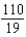
E)
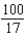

Unlock Deck
Unlock for access to all 23 flashcards in this deck.
Unlock Deck
k this deck
19
Suppose the annual spending by tourists in a resort city is $100 million. Approximately 90% of that revenue is again spent in the resort city, and of that amount approximately 90% is again spent in the same city, and so on. Write the expression that gives the total amount of spending generated by the $100 million after n years.
A)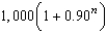 million dollars
million dollars
B)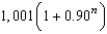 million dollars
million dollars
C)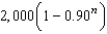 million dollars
million dollars
D)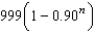 million dollars
million dollars
E)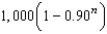 million dollars
million dollars
A)
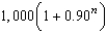 million dollars
million dollarsB)
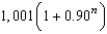 million dollars
million dollarsC)
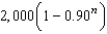 million dollars
million dollarsD)
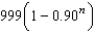 million dollars
million dollarsE)
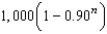 million dollars
million dollars
Unlock Deck
Unlock for access to all 23 flashcards in this deck.
Unlock Deck
k this deck
20
Find the sum of the convergent series. 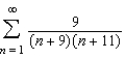
A)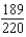
B)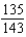
C)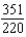
D)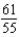
E)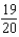
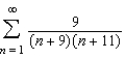
A)
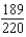
B)
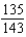
C)
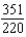
D)
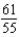
E)
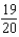

Unlock Deck
Unlock for access to all 23 flashcards in this deck.
Unlock Deck
k this deck
21
Suppose you go to work at a company that pays $0.08 for the first day, $0.16 for the second day, $0.32 for the third day, and so on. If the daily wage keeps doubling, what would your total income be for working 29 days? Round your answer to two decimal places.
A) $21,474,836.48
B) $10,737,418.24
C) $42,949,672.88
D) $171,798,691.52
E) $85,899,345.76
A) $21,474,836.48
B) $10,737,418.24
C) $42,949,672.88
D) $171,798,691.52
E) $85,899,345.76

Unlock Deck
Unlock for access to all 23 flashcards in this deck.
Unlock Deck
k this deck
22
Suppose the winner of a $4,000,000 sweepstakes will be paid $100,000 per year for 40 years, starting a year from now. The money earns 5% interest per year. The present value of the winnings is 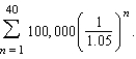 Compute the present value using the formula for the nth partial sum of a geometric series. Round your answer to two decimal places.
Compute the present value using the formula for the nth partial sum of a geometric series. Round your answer to two decimal places.
A) $6,852,274.09
B) $1,959,646.05
C) $4,568,182.73
D) $1,246,221.03
E) $1,715,908.64
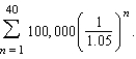 Compute the present value using the formula for the nth partial sum of a geometric series. Round your answer to two decimal places.
Compute the present value using the formula for the nth partial sum of a geometric series. Round your answer to two decimal places.A) $6,852,274.09
B) $1,959,646.05
C) $4,568,182.73
D) $1,246,221.03
E) $1,715,908.64

Unlock Deck
Unlock for access to all 23 flashcards in this deck.
Unlock Deck
k this deck
23
Suppose a ball is dropped from a height of 16 feet. Each time it drops h feet, it rebounds 0.85h feet. Find the total distance traveled by the ball. Round your answer to two decimal places.
A) 229.33 feet
B) 410.67 feet
C) 181.33 feet
D) 197.33 feet
E) 213.33 feet
A) 229.33 feet
B) 410.67 feet
C) 181.33 feet
D) 197.33 feet
E) 213.33 feet

Unlock Deck
Unlock for access to all 23 flashcards in this deck.
Unlock Deck
k this deck


