Deck 15: Section 8: Vector Analysis
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/17
Play
Full screen (f)
Deck 15: Section 8: Vector Analysis
1
Let 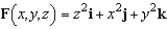 and let S be the graph of
and let S be the graph of 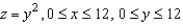 . Verify Stokes's Theorem by evaluating
. Verify Stokes's Theorem by evaluating 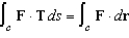 as a line integral and as a double integral.
as a line integral and as a double integral.
A)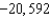
B)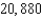
C)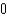
D)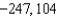
E)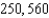
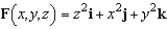 and let S be the graph of
and let S be the graph of 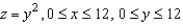 . Verify Stokes's Theorem by evaluating
. Verify Stokes's Theorem by evaluating 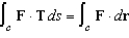 as a line integral and as a double integral.
as a line integral and as a double integral.A)
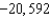
B)
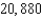
C)
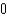
D)
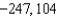
E)
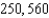
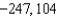
2
Let 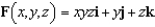 and let S be the plane
and let S be the plane 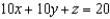 in the first octant. Verify Stokes's Theorem by evaluating
in the first octant. Verify Stokes's Theorem by evaluating 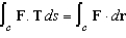 as a line integral and as a double integral.
as a line integral and as a double integral.
A)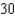
B)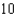
C)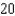
D) 0
E) 1
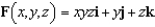 and let S be the plane
and let S be the plane 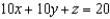 in the first octant. Verify Stokes's Theorem by evaluating
in the first octant. Verify Stokes's Theorem by evaluating 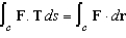 as a line integral and as a double integral.
as a line integral and as a double integral.A)
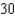
B)
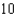
C)
D) 0
E) 1
0
3
Find the curl of the vector field 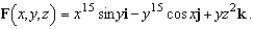
A)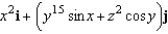
B)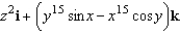
C)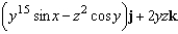
D)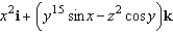
E)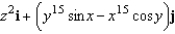
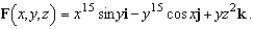
A)
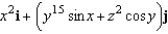
B)
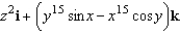
C)
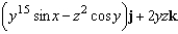
D)
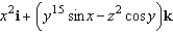
E)
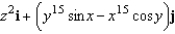
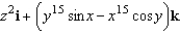
4
Use Stokes's Theorem to evaluate 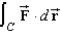 .Use a computer algebra system to verify your results. Note: C is oriented counterclockwise as viewed from above.
.Use a computer algebra system to verify your results. Note: C is oriented counterclockwise as viewed from above. 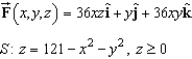
A)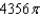
B)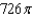
C)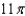
D)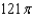
E)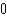
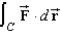 .Use a computer algebra system to verify your results. Note: C is oriented counterclockwise as viewed from above.
.Use a computer algebra system to verify your results. Note: C is oriented counterclockwise as viewed from above. 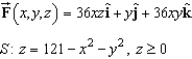
A)
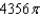
B)
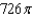
C)
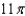
D)
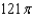
E)
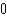

Unlock Deck
Unlock for access to all 17 flashcards in this deck.
Unlock Deck
k this deck
5
Use Stokes's Theorem to evaluate 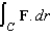 where
where 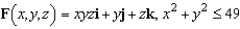 and S is the first-octant portion of
and S is the first-octant portion of 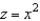 over
over 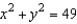 . Use a computer algebra system to verify your result.
. Use a computer algebra system to verify your result.
A)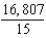
B)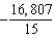
C)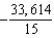
D)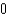
E)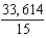
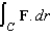 where
where 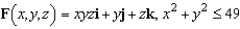 and S is the first-octant portion of
and S is the first-octant portion of 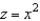 over
over 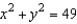 . Use a computer algebra system to verify your result.
. Use a computer algebra system to verify your result.A)
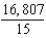
B)
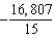
C)
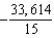
D)
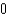
E)
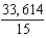

Unlock Deck
Unlock for access to all 17 flashcards in this deck.
Unlock Deck
k this deck
6
Use Stokes's Theorem to evaluate 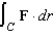 where
where 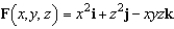 and S is
and S is 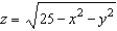 .Use a computer algebra system to verify your result.
.Use a computer algebra system to verify your result.
A)
B)
C)
D)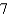
E)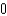
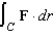 where
where 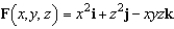 and S is
and S is 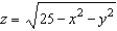 .Use a computer algebra system to verify your result.
.Use a computer algebra system to verify your result.A)
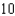
B)
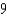
C)
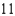
D)
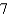
E)

Unlock Deck
Unlock for access to all 17 flashcards in this deck.
Unlock Deck
k this deck
7
Find the curl of the vector field 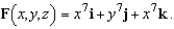
A)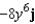
B)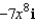
C)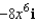
D)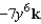
E)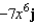
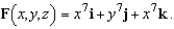
A)
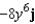
B)
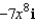
C)
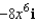
D)
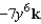
E)

Unlock Deck
Unlock for access to all 17 flashcards in this deck.
Unlock Deck
k this deck
8
Find the curl of the vector field 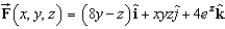 .
.
A)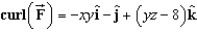
B)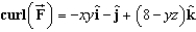
C)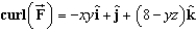
D)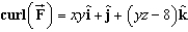
E)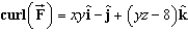
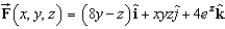 .
.A)
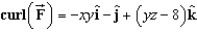
B)
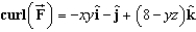
C)
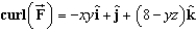
D)
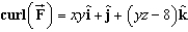
E)
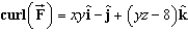

Unlock Deck
Unlock for access to all 17 flashcards in this deck.
Unlock Deck
k this deck
9
Use Stokes's Theorem to evaluate 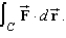 Use a computer algebra system to verify your results. Note: C is oriented counterclockwise as viewed from above.
Use a computer algebra system to verify your results. Note: C is oriented counterclockwise as viewed from above. 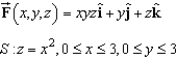
A)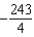
B)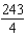
C)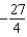
D)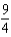
E)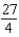
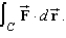 Use a computer algebra system to verify your results. Note: C is oriented counterclockwise as viewed from above.
Use a computer algebra system to verify your results. Note: C is oriented counterclockwise as viewed from above. 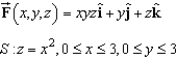
A)
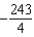
B)
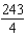
C)
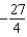
D)
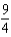
E)
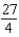

Unlock Deck
Unlock for access to all 17 flashcards in this deck.
Unlock Deck
k this deck
10
Find the curl of the vector field 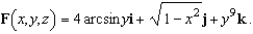
A)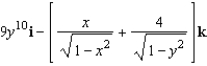
B)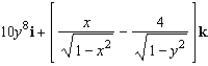
C)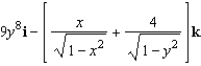
D)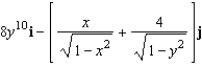
E)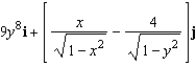
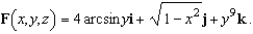
A)
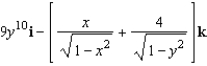
B)
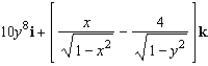
C)
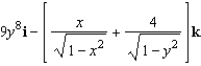
D)
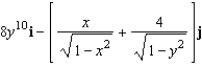
E)
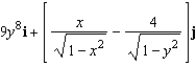

Unlock Deck
Unlock for access to all 17 flashcards in this deck.
Unlock Deck
k this deck
11
The motion of a liquid in a cylindrical container of radius 1 is described by the velocity field 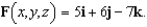 Find
Find 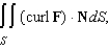 where S is the upper surface of the cylindrical container.
where S is the upper surface of the cylindrical container.
A)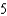
B)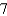
C)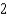
D) 0
E)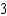
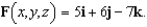 Find
Find 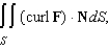 where S is the upper surface of the cylindrical container.
where S is the upper surface of the cylindrical container.A)
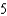
B)
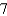
C)
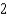
D) 0
E)
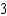

Unlock Deck
Unlock for access to all 17 flashcards in this deck.
Unlock Deck
k this deck
12
Verify Stokes's Theorem by evaluating 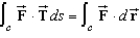 as a line integral and as a double integral .
as a line integral and as a double integral . 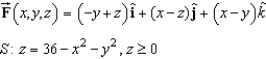
A)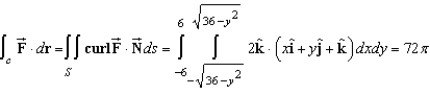
B)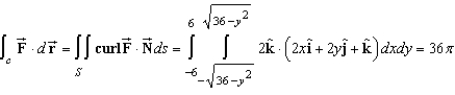
C)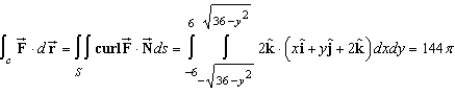
D)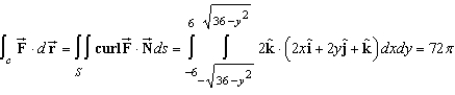
E)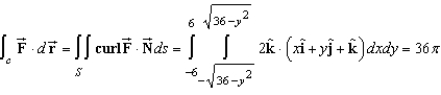
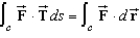 as a line integral and as a double integral .
as a line integral and as a double integral . 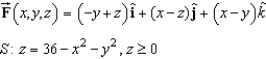
A)
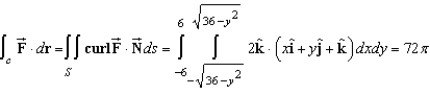
B)
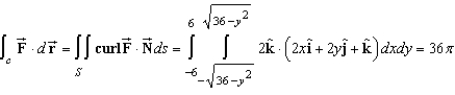
C)
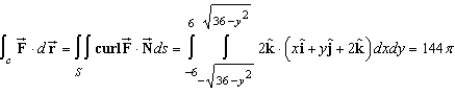
D)
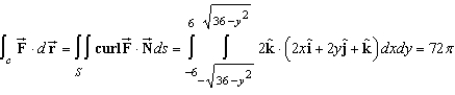
E)
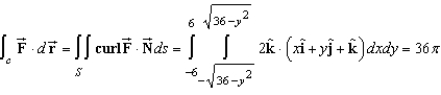

Unlock Deck
Unlock for access to all 17 flashcards in this deck.
Unlock Deck
k this deck
13
Let 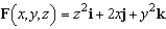 and let S be the graph of
and let S be the graph of 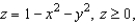 oriented counterclockwise. Use Stokes's Theorem to evaluate
oriented counterclockwise. Use Stokes's Theorem to evaluate 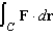 .
.
A)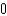
B)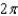
C)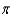
D)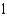
E)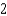
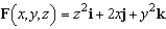 and let S be the graph of
and let S be the graph of 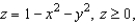 oriented counterclockwise. Use Stokes's Theorem to evaluate
oriented counterclockwise. Use Stokes's Theorem to evaluate 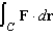 .
.A)
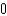
B)
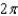
C)
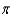
D)
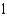
E)
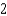

Unlock Deck
Unlock for access to all 17 flashcards in this deck.
Unlock Deck
k this deck
14
The motion of a liquid in a cylindrical container of radius 1 is described by the velocity field 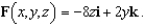 Find
Find 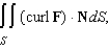 where S is the upper surface of the cylindrical container.
where S is the upper surface of the cylindrical container.
A)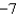
B)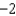
C)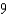
D)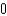
E)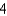
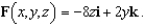 Find
Find 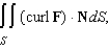 where S is the upper surface of the cylindrical container.
where S is the upper surface of the cylindrical container.A)
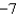
B)
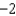
C)
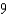
D)
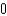
E)
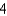

Unlock Deck
Unlock for access to all 17 flashcards in this deck.
Unlock Deck
k this deck
15
Use Stokes's Theorem to evaluate 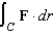 where
where 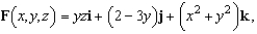
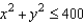 and S is the first-octant portion of
and S is the first-octant portion of 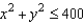 over
over 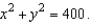 Use a computer algebra system to verify your result.
Use a computer algebra system to verify your result.
A)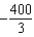
B)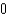
C)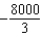
D)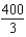
E)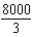
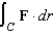 where
where 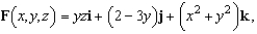
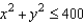 and S is the first-octant portion of
and S is the first-octant portion of 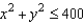 over
over 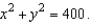 Use a computer algebra system to verify your result.
Use a computer algebra system to verify your result.A)
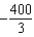
B)
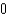
C)
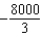
D)
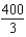
E)
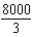

Unlock Deck
Unlock for access to all 17 flashcards in this deck.
Unlock Deck
k this deck
16
Use Stokes's Theorem to evaluate 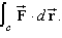 Use a computer algebra system to verify your results. Note: C is oriented counterclockwise as viewed from above.
Use a computer algebra system to verify your results. Note: C is oriented counterclockwise as viewed from above. 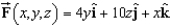 C: triangle with vertices
C: triangle with vertices 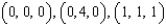
A)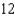
B)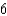
C)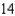
D)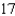
E)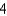
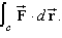 Use a computer algebra system to verify your results. Note: C is oriented counterclockwise as viewed from above.
Use a computer algebra system to verify your results. Note: C is oriented counterclockwise as viewed from above. 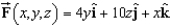 C: triangle with vertices
C: triangle with vertices 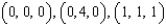
A)
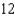
B)
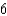
C)
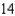
D)
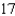
E)
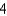

Unlock Deck
Unlock for access to all 17 flashcards in this deck.
Unlock Deck
k this deck
17
Use Stokes's Theorem to evaluate 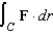 where
where 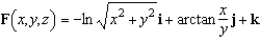 and S is
and S is 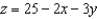 over
over 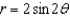 in the first octant. Use a computer algebra system to verify your result.
in the first octant. Use a computer algebra system to verify your result.
A) 0
B)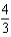
C)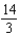
D)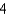
E)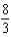
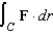 where
where 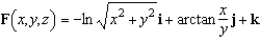 and S is
and S is 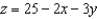 over
over 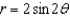 in the first octant. Use a computer algebra system to verify your result.
in the first octant. Use a computer algebra system to verify your result.A) 0
B)
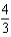
C)
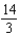
D)
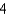
E)
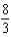

Unlock Deck
Unlock for access to all 17 flashcards in this deck.
Unlock Deck
k this deck


