Deck 14: Section 6: Multiple Integration
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/19
Play
Full screen (f)
Deck 14: Section 6: Multiple Integration
1
Find the center of mass of the solid bounded by 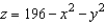 and
and 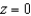 with density function
with density function 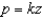 .
.
A)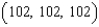
B)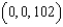
C)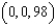
D)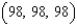
E)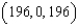
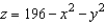 and
and 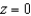 with density function
with density function 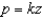 .
.A)
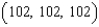
B)
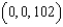
C)
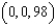
D)
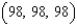
E)
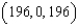
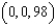
2
Evaluate the iterated integral 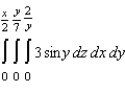 .
.
A)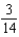
B)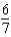
C)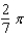
D)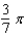
E)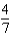
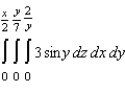 .
.A)
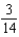
B)
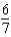
C)
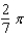
D)
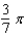
E)
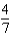
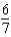
3
Find 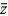 of the center of mass of the solid of given density
of the center of mass of the solid of given density 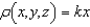 bounded by the graphs of the equations
bounded by the graphs of the equations 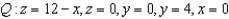 .
.
A)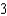
B)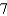
C)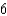
D)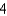
E)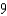
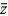 of the center of mass of the solid of given density
of the center of mass of the solid of given density 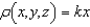 bounded by the graphs of the equations
bounded by the graphs of the equations 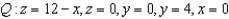 .
.A)
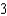
B)
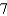
C)
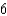
D)
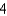
E)
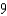
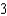
4
Find the average value of 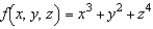 over the region Q, where Q is a cube in the first octant bounded by the coordinate planes, and the planes
over the region Q, where Q is a cube in the first octant bounded by the coordinate planes, and the planes 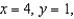 and
and 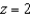 . The average value of a continuous function
. The average value of a continuous function 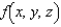 over a solid region Q is
over a solid region Q is 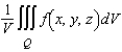 , where V is the volume of the solid region Q.
, where V is the volume of the solid region Q.
A)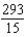
B)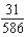
C)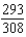
D)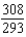
E)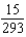
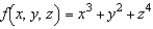 over the region Q, where Q is a cube in the first octant bounded by the coordinate planes, and the planes
over the region Q, where Q is a cube in the first octant bounded by the coordinate planes, and the planes 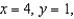 and
and 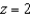 . The average value of a continuous function
. The average value of a continuous function 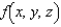 over a solid region Q is
over a solid region Q is 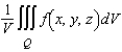 , where V is the volume of the solid region Q.
, where V is the volume of the solid region Q.A)
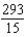
B)
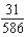
C)
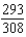
D)
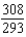
E)
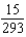

Unlock Deck
Unlock for access to all 19 flashcards in this deck.
Unlock Deck
k this deck
5
Find the centroid of the solid region bounded by the graphs of the equations. Use a computer algebra system to evaluate the triple integral. (Assume uniform density and find the center of mass.) 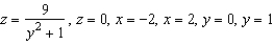
A)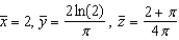
B)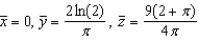
C)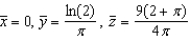
D)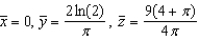
E)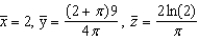
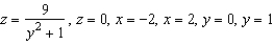
A)
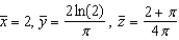
B)
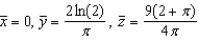
C)
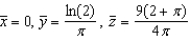
D)
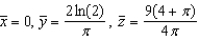
E)
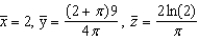

Unlock Deck
Unlock for access to all 19 flashcards in this deck.
Unlock Deck
k this deck
6
Find the average value of 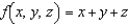 over the region Q, where Q is a tetrahedron in the first octant with vertices
over the region Q, where Q is a tetrahedron in the first octant with vertices 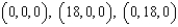 and
and 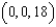 . The average value of a continuous function
. The average value of a continuous function 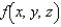 over a solid region Q is
over a solid region Q is 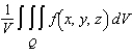 , where V is the volume of the solid region Q.
, where V is the volume of the solid region Q.
A)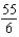
B)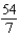
C)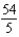
D)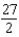
E)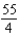
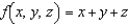 over the region Q, where Q is a tetrahedron in the first octant with vertices
over the region Q, where Q is a tetrahedron in the first octant with vertices 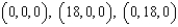 and
and 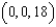 . The average value of a continuous function
. The average value of a continuous function 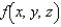 over a solid region Q is
over a solid region Q is 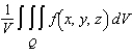 , where V is the volume of the solid region Q.
, where V is the volume of the solid region Q.A)
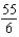
B)
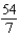
C)
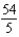
D)
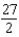
E)
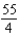

Unlock Deck
Unlock for access to all 19 flashcards in this deck.
Unlock Deck
k this deck
7
Use a triple integral to find the volume of the solid bounded by the graphs of the equations 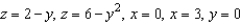 .
.
A)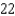
B)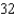
C)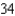
D)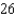
E)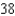
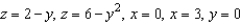 .
.A)
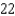
B)
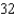
C)
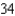
D)
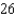
E)
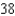

Unlock Deck
Unlock for access to all 19 flashcards in this deck.
Unlock Deck
k this deck
8
Evaluate the following iterated integral. 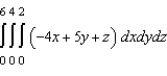
A)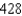
B)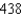
C)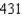
D)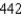
E)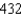
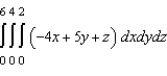
A)
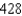
B)
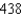
C)
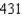
D)
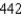
E)
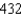

Unlock Deck
Unlock for access to all 19 flashcards in this deck.
Unlock Deck
k this deck
9
Find 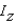 for the indicated solid with density function
for the indicated solid with density function 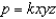 .
. 
A)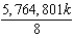
B)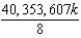
C)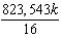
D)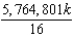
E)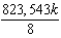
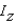 for the indicated solid with density function
for the indicated solid with density function 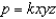 .
. 
A)
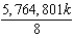
B)
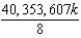
C)
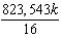
D)
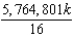
E)
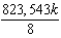

Unlock Deck
Unlock for access to all 19 flashcards in this deck.
Unlock Deck
k this deck
10
Evaluate the following iterated integral. 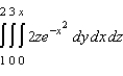
A)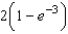
B)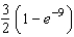
C)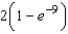
D)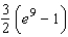
E)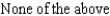
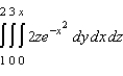
A)
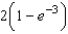
B)
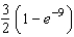
C)
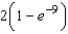
D)
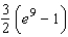
E)

Unlock Deck
Unlock for access to all 19 flashcards in this deck.
Unlock Deck
k this deck
11
Set up a triple integral for the volume of the solid bounded above by the cylinder 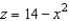 and below by the paraboloid
and below by the paraboloid 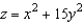 .
.
A)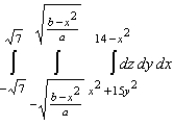
B)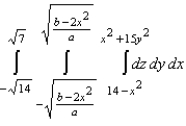
C)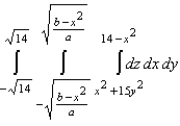
D)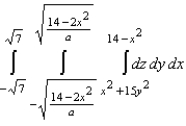
E)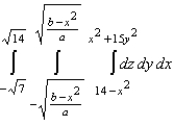
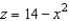 and below by the paraboloid
and below by the paraboloid 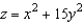 .
.A)
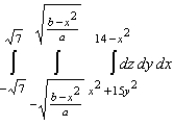
B)
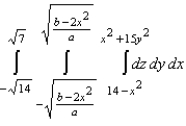
C)
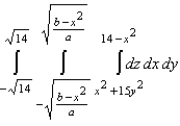
D)
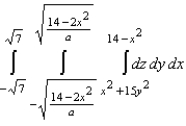
E)
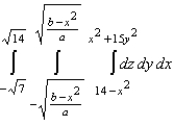

Unlock Deck
Unlock for access to all 19 flashcards in this deck.
Unlock Deck
k this deck
12
Determine the value of b so that the volume of the ellipsoid 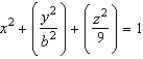 is
is 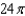 .
.
A)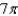
B)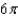
C)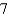
D)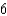
E)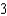
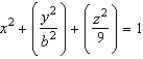 is
is 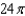 .
.A)
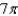
B)
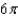
C)
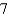
D)
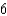
E)
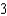

Unlock Deck
Unlock for access to all 19 flashcards in this deck.
Unlock Deck
k this deck
13
Set up a triple integral that gives the moment of inertia about the 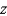 -axis of the solid region Q of density given below.
-axis of the solid region Q of density given below. 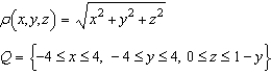
A)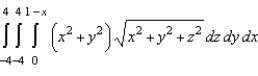
B)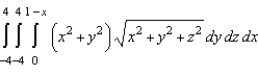
C)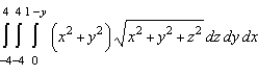
D)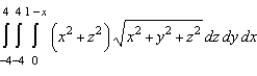
E)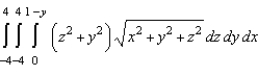
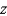 -axis of the solid region Q of density given below.
-axis of the solid region Q of density given below. 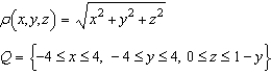
A)
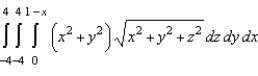
B)
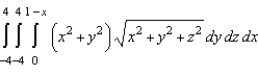
C)
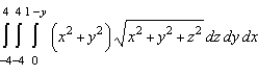
D)
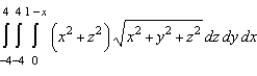
E)
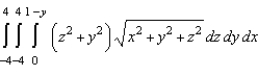

Unlock Deck
Unlock for access to all 19 flashcards in this deck.
Unlock Deck
k this deck
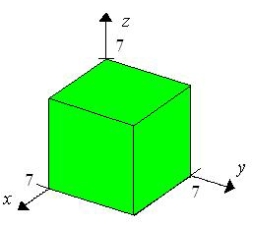
14
Use a triple integral to find the volume of the solid shown below. 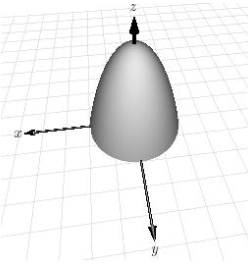
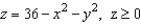
A)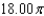
B)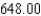
C)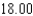
D)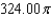
E)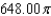

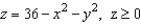
A)
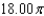
B)
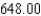
C)
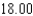
D)
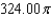
E)
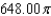

Unlock Deck
Unlock for access to all 19 flashcards in this deck.
Unlock Deck
k this deck
15
Use a triple integral to find the volume of the solid shown below. 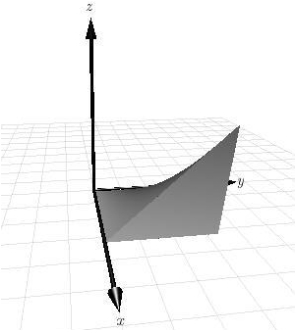
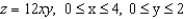
A)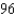
B)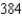
C)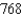
D)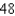
E)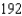

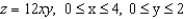
A)
B)
C)
D)
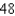
E)
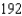

Unlock Deck
Unlock for access to all 19 flashcards in this deck.
Unlock Deck
k this deck
16
Rewrite the iterated integral 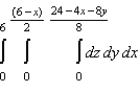 using the order
using the order 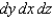 .
.
A)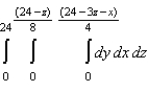
B)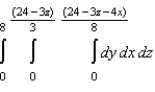
C)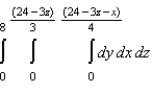
D)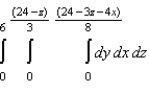
E)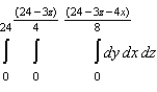
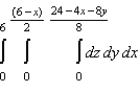 using the order
using the order  .
.A)
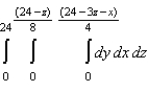
B)
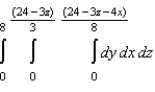
C)
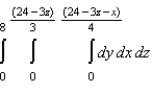
D)
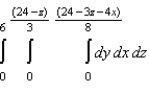
E)
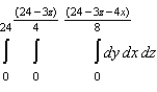

Unlock Deck
Unlock for access to all 19 flashcards in this deck.
Unlock Deck
k this deck
17
Set up a triple integral for the volume of the solid bounded by 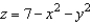 and
and 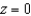 .
.
A)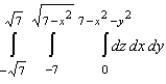
B)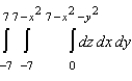
C)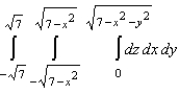
D)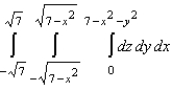
E)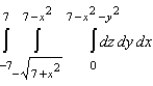
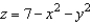 and
and 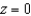 .
.A)
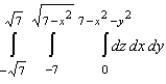
B)
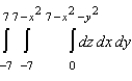
C)
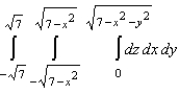
D)
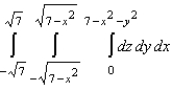
E)
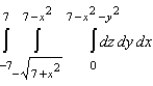

Unlock Deck
Unlock for access to all 19 flashcards in this deck.
Unlock Deck
k this deck
18
Sketch the solid whose volume is given by the iterated integral given below and use the sketch to rewrite the integral using the indicated order of integration. 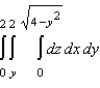 Rewrite the integral using the order
Rewrite the integral using the order 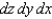 .
.
A)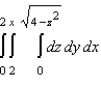
B)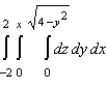
C)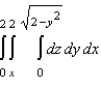
D)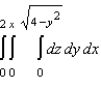
E)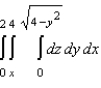
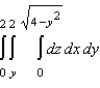 Rewrite the integral using the order
Rewrite the integral using the order 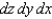 .
.A)
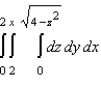
B)
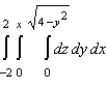
C)
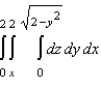
D)
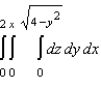
E)
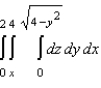

Unlock Deck
Unlock for access to all 19 flashcards in this deck.
Unlock Deck
k this deck
19
Set up a triple integral for the volume of the solid bounded by the coordinate planes and the plane given below. 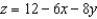
A)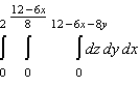
B)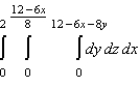
C)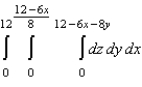
D)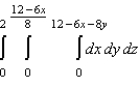
E)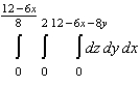
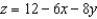
A)
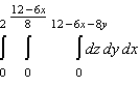
B)
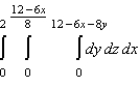
C)
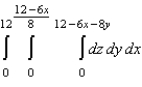
D)
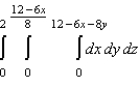
E)
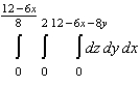

Unlock Deck
Unlock for access to all 19 flashcards in this deck.
Unlock Deck
k this deck


