Deck 14: Section 1: Multiple Integration
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/20
Play
Full screen (f)
Deck 14: Section 1: Multiple Integration
1
Sketch the region R and evaluate the iterated integral. 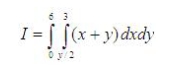
A)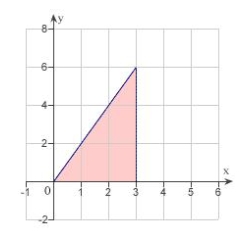
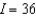
B)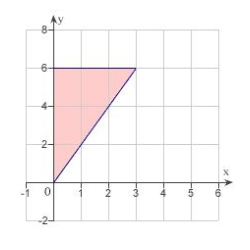
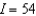
C)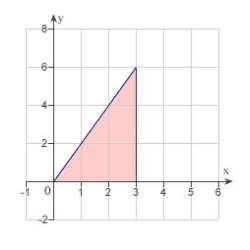
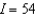
D)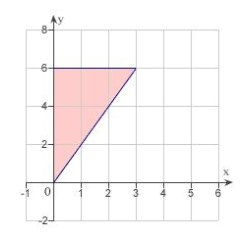
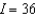
E)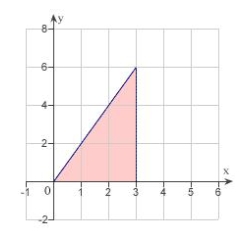
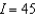
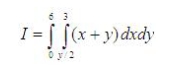
A)

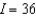
B)

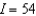
C)

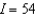
D)

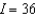
E)

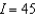

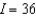
2
Use an iterated integral to find the area of the region bounded by 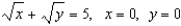 .
.
A)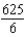
B)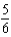
C)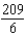
D)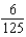
E) The integral is improper and does not converge.
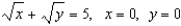 .
.A)
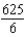
B)
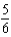
C)
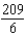
D)
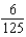
E) The integral is improper and does not converge.
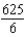
3
Evaluate the following integral. 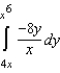
A)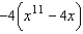
B)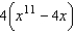
C)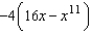
D)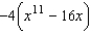
E)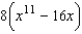
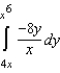
A)
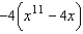
B)
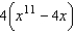
C)
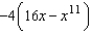
D)
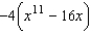
E)
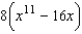
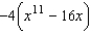
4
Evaluate the following iterated integral. 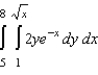
A)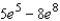
B)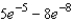
C)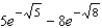
D)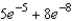
E)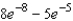
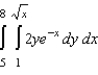
A)
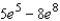
B)
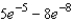
C)
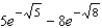
D)
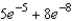
E)
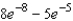

Unlock Deck
Unlock for access to all 20 flashcards in this deck.
Unlock Deck
k this deck
5
Evaluate the following iterated integral. 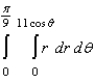
A)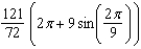
B)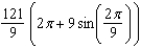
C)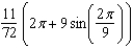
D)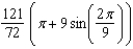
E)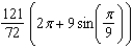
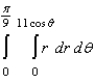
A)
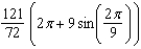
B)
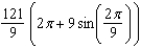
C)
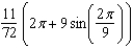
D)
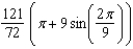
E)
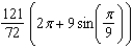

Unlock Deck
Unlock for access to all 20 flashcards in this deck.
Unlock Deck
k this deck
6
Evaluate the improper iterated integral 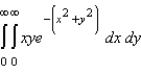 .
.
A)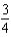
B)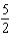
C)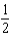
D)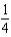
E)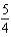
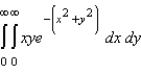 .
.A)
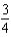
B)
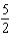
C)
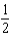
D)
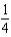
E)
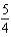

Unlock Deck
Unlock for access to all 20 flashcards in this deck.
Unlock Deck
k this deck
7
Use an iterated integral to find the area of the region shown in the figure below. 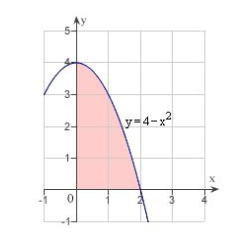
A)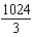
B)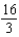
C)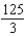
D)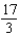
E)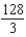

A)
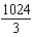
B)
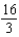
C)
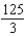
D)
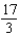
E)
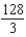

Unlock Deck
Unlock for access to all 20 flashcards in this deck.
Unlock Deck
k this deck
8
Evaluate the iterated integral 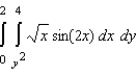 by switching the order of integration. Round your answer to three decimal places.
by switching the order of integration. Round your answer to three decimal places.
A) 0.538
B) 0.558
C) 30.538
D) 1.538
E) 4.538
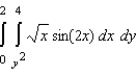 by switching the order of integration. Round your answer to three decimal places.
by switching the order of integration. Round your answer to three decimal places.A) 0.538
B) 0.558
C) 30.538
D) 1.538
E) 4.538

Unlock Deck
Unlock for access to all 20 flashcards in this deck.
Unlock Deck
k this deck
9
The area of a region R is given by the iterated integral 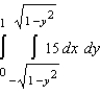 . Switch the order of integration and show that both orders yield the same area. What is this area?
. Switch the order of integration and show that both orders yield the same area. What is this area?
A)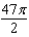
B)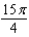
C)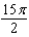
D)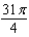
E)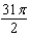
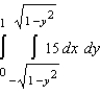 . Switch the order of integration and show that both orders yield the same area. What is this area?
. Switch the order of integration and show that both orders yield the same area. What is this area?A)
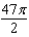
B)
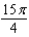
C)
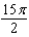
D)
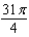
E)
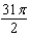

Unlock Deck
Unlock for access to all 20 flashcards in this deck.
Unlock Deck
k this deck
10
Evaluate the following improper integral. 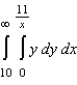
A)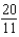
B)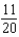
C)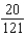
D)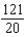
E) The integral does not converge.
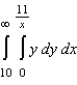
A)
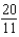
B)
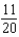
C)
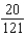
D)
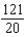
E) The integral does not converge.

Unlock Deck
Unlock for access to all 20 flashcards in this deck.
Unlock Deck
k this deck
11
Evaluate the following integral. 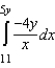
A)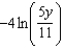
B)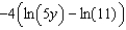
C)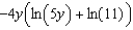
D)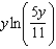
E)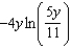
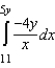
A)
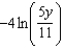
B)
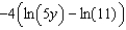
C)
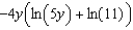
D)
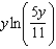
E)
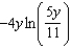

Unlock Deck
Unlock for access to all 20 flashcards in this deck.
Unlock Deck
k this deck
12
Evaluate the following iterated integral. 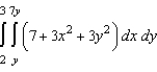
A) 5,901
B) 5,931
C) 5,955
D) 5,970
E) 6,017
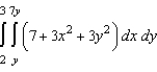
A) 5,901
B) 5,931
C) 5,955
D) 5,970
E) 6,017

Unlock Deck
Unlock for access to all 20 flashcards in this deck.
Unlock Deck
k this deck
13
Sketch the region R of integration and then switch the order of integration for the following integral. 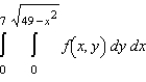
A)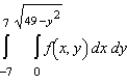
B)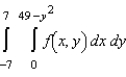
C)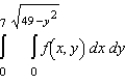
D)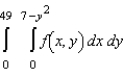
E)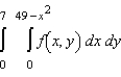
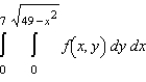
A)
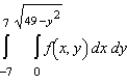
B)
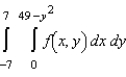
C)
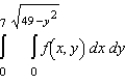
D)
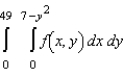
E)
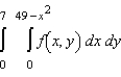

Unlock Deck
Unlock for access to all 20 flashcards in this deck.
Unlock Deck
k this deck
14
Evaluate the following iterated integral. 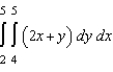
A) 41.5
B) 38.5
C) 34.5
D) 33.5
E) 37.5
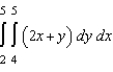
A) 41.5
B) 38.5
C) 34.5
D) 33.5
E) 37.5

Unlock Deck
Unlock for access to all 20 flashcards in this deck.
Unlock Deck
k this deck
15
Evaluate the iterated integral below. Note that it is necessary to switch the order of integration. 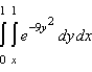
A)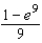
B)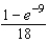
C)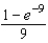
D)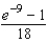
E)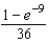
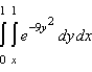
A)
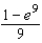
B)
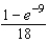
C)
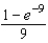
D)
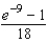
E)
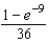

Unlock Deck
Unlock for access to all 20 flashcards in this deck.
Unlock Deck
k this deck
16
Use an iterated integral to find the area of the region bounded by 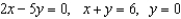 .
.
A)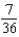
B)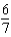
C)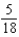
D)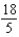
E)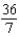
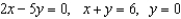 .
.A)
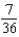
B)
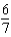
C)
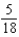
D)
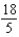
E)
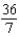

Unlock Deck
Unlock for access to all 20 flashcards in this deck.
Unlock Deck
k this deck
17
The area of a region R is given by the iterated integral 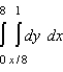 . Switch the order of integration and show that both orders yield the same area. What is this area?
. Switch the order of integration and show that both orders yield the same area. What is this area?
A) 65
B) 16
C) 21
D) 8
E) 4
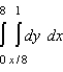 . Switch the order of integration and show that both orders yield the same area. What is this area?
. Switch the order of integration and show that both orders yield the same area. What is this area?A) 65
B) 16
C) 21
D) 8
E) 4

Unlock Deck
Unlock for access to all 20 flashcards in this deck.
Unlock Deck
k this deck
18
Use an iterated integral to find the area of the region bounded by the graphs of the equations 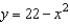 and
and 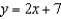 .
.
A)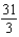
B)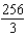
C)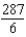
D)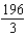
E)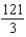
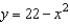 and
and 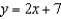 .
.A)
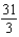
B)
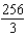
C)
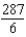
D)
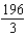
E)
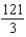

Unlock Deck
Unlock for access to all 20 flashcards in this deck.
Unlock Deck
k this deck
19
The area of a region R is given by the iterated integrals 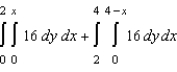 . Switch the order of integration and show that both orders yield the same area. What is this area?
. Switch the order of integration and show that both orders yield the same area. What is this area?
A) 32
B) 1025
C) 64
D) 771
E) 63
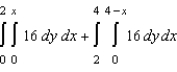 . Switch the order of integration and show that both orders yield the same area. What is this area?
. Switch the order of integration and show that both orders yield the same area. What is this area?A) 32
B) 1025
C) 64
D) 771
E) 63

Unlock Deck
Unlock for access to all 20 flashcards in this deck.
Unlock Deck
k this deck
20
Evaluate the following integral. 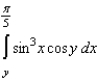
A)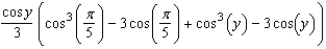
B)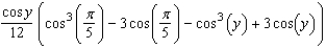
C)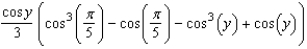
D)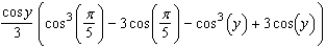
E)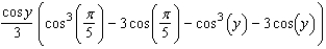
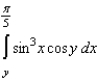
A)
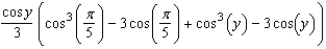
B)
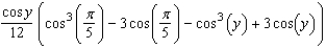
C)
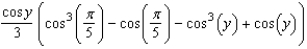
D)
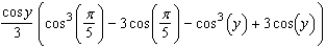
E)
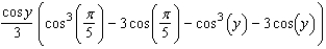

Unlock Deck
Unlock for access to all 20 flashcards in this deck.
Unlock Deck
k this deck


