Deck 8: Techniques of Integration
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/101
Play
Full screen (f)
Deck 8: Techniques of Integration
1
To evaluate the integral 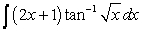 using Integration by Parts, we should choose:
using Integration by Parts, we should choose:
A)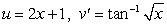 .
.
B)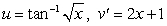 .
.
C)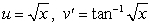 .
.
D)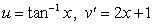 .
.
E)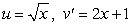 .
.
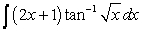 using Integration by Parts, we should choose:
using Integration by Parts, we should choose:A)
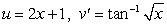 .
.B)
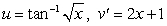 .
.C)
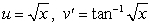 .
.D)
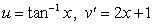 .
.E)
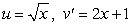 .
.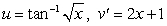 .
. 2
To evaluate the integral 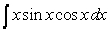 using integration by parts, the convenient choice is :
using integration by parts, the convenient choice is :
A)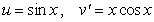 .
.
B)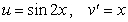 .
.
C)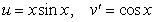 .
.
D)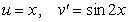 .
.
E)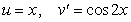 .
.
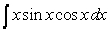 using integration by parts, the convenient choice is :
using integration by parts, the convenient choice is :A)
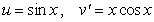 .
.B)
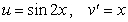 .
.C)
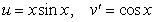 .
.D)
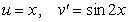 .
.E)
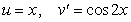 .
.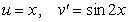 .
. 3
Evaluate the integral using one or two methods, as indicated.
A)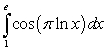 : the Substitution Method followed by Integration by Parts, twice.
: the Substitution Method followed by Integration by Parts, twice.
B)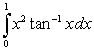 : Integration by Parts followed by the Substitution Method.
: Integration by Parts followed by the Substitution Method.
A)
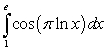 : the Substitution Method followed by Integration by Parts, twice.
: the Substitution Method followed by Integration by Parts, twice. B)
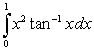 : Integration by Parts followed by the Substitution Method.
: Integration by Parts followed by the Substitution Method.A) 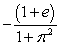 B)
B) 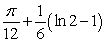
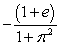 B)
B) 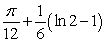
4
Use the substitution 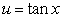 and the trigonometric identity
and the trigonometric identity 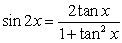 to evaluate the integral.
to evaluate the integral. 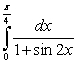
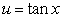 and the trigonometric identity
and the trigonometric identity 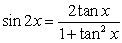 to evaluate the integral.
to evaluate the integral. 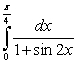

Unlock Deck
Unlock for access to all 101 flashcards in this deck.
Unlock Deck
k this deck
5
Compute the integrals using the reduction formulas, or the substitution 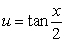 , and the identities
, and the identities 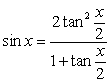 ,
, 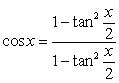 , as required.
, as required.
A)
B)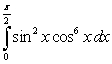
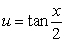 , and the identities
, and the identities 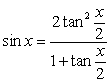 ,
, 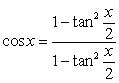 , as required.
, as required. A)
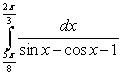
B)
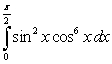

Unlock Deck
Unlock for access to all 101 flashcards in this deck.
Unlock Deck
k this deck
6
Compute the integral 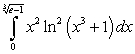 .
.
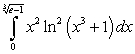 .
.
Unlock Deck
Unlock for access to all 101 flashcards in this deck.
Unlock Deck
k this deck
7
Evaluate the integrals using Integration by Parts, the Substitution Method, or both methods.
A)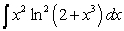
B)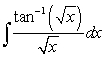
A)
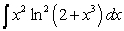
B)
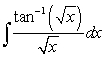

Unlock Deck
Unlock for access to all 101 flashcards in this deck.
Unlock Deck
k this deck
8
Compute the following integrals.
A)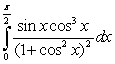
B)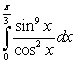
A)
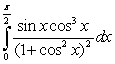
B)
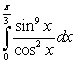

Unlock Deck
Unlock for access to all 101 flashcards in this deck.
Unlock Deck
k this deck
9
For computing the integral 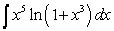 , the most efficient method is
, the most efficient method is
A) Integration by Parts with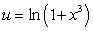 and
and 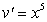 .
.
B) substitution of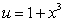 followed by Integration by Parts.
followed by Integration by Parts.
C) Integration by Parts, twice.
D) Integration by Parts with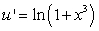 and
and 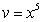 .
.
E) None of the methods covered so far is efficient in computing this integral.
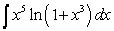 , the most efficient method is
, the most efficient method isA) Integration by Parts with
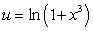 and
and 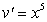 .
.B) substitution of
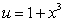 followed by Integration by Parts.
followed by Integration by Parts.C) Integration by Parts, twice.
D) Integration by Parts with
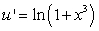 and
and 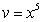 .
.E) None of the methods covered so far is efficient in computing this integral.

Unlock Deck
Unlock for access to all 101 flashcards in this deck.
Unlock Deck
k this deck
10
The value of the integral 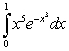 is:
is:
A)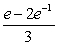 .
.
B)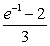 .
.
C)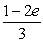 .
.
D)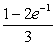 .
.
E)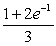 .
.
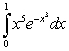 is:
is:A)
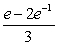 .
.B)
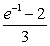 .
.C)
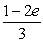 .
.D)
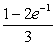 .
.E)
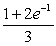 .
.
Unlock Deck
Unlock for access to all 101 flashcards in this deck.
Unlock Deck
k this deck
11
Use the substitution 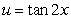 and the trigonometric identity
and the trigonometric identity 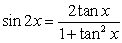 , or reduction formulas as necessary, to calculate the integrals.
, or reduction formulas as necessary, to calculate the integrals.
A)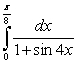
B)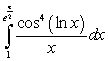
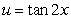 and the trigonometric identity
and the trigonometric identity 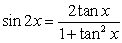 , or reduction formulas as necessary, to calculate the integrals.
, or reduction formulas as necessary, to calculate the integrals. A)
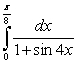
B)
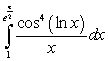

Unlock Deck
Unlock for access to all 101 flashcards in this deck.
Unlock Deck
k this deck
12
Evaluate the integral 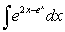 .
.
A)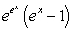
B)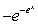
C)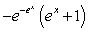
D)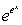
E)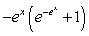
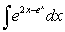 .
.A)
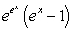
B)
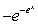
C)
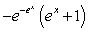
D)
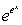
E)
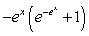

Unlock Deck
Unlock for access to all 101 flashcards in this deck.
Unlock Deck
k this deck
13
Compute the integral 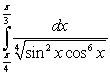 .
.
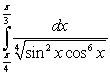 .
.
Unlock Deck
Unlock for access to all 101 flashcards in this deck.
Unlock Deck
k this deck
14
Evaluate the integrals using Integration by Parts, the Substitution Method, or both methods.
A)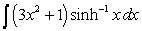
B)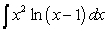 . (Hint: Use
. (Hint: Use 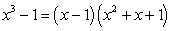 .
.
A)
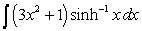
B)
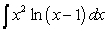 . (Hint: Use
. (Hint: Use 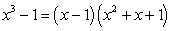 .
.
Unlock Deck
Unlock for access to all 101 flashcards in this deck.
Unlock Deck
k this deck
15
To evaluate the integral 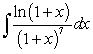 by Integration by Parts, the convenient choice is
by Integration by Parts, the convenient choice is
A)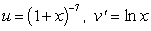
B)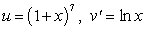
C)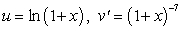
D)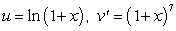
E)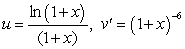
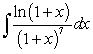 by Integration by Parts, the convenient choice is
by Integration by Parts, the convenient choice isA)
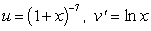
B)
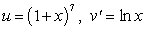
C)
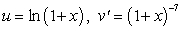
D)
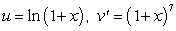
E)
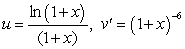

Unlock Deck
Unlock for access to all 101 flashcards in this deck.
Unlock Deck
k this deck
16
Evaluate the integrals.
A)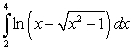
B)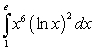
A)
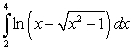
B)
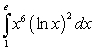

Unlock Deck
Unlock for access to all 101 flashcards in this deck.
Unlock Deck
k this deck
17
To evaluate the integral 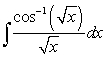 using Integration by Parts, we should choose:
using Integration by Parts, we should choose:
A)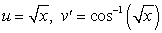 .
.
B)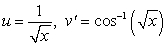 .
.
C)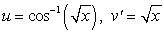 .
.
D)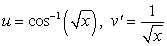 .
.
E)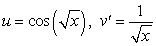 .
.
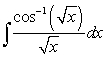 using Integration by Parts, we should choose:
using Integration by Parts, we should choose:A)
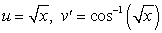 .
.B)
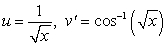 .
.C)
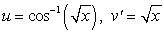 .
.D)
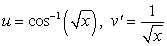 .
.E)
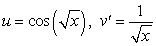 .
.
Unlock Deck
Unlock for access to all 101 flashcards in this deck.
Unlock Deck
k this deck
18
Evaluate the integral 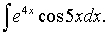
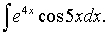

Unlock Deck
Unlock for access to all 101 flashcards in this deck.
Unlock Deck
k this deck
19
Evaluate the integral 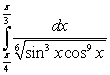 .
.
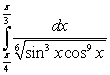 .
.
Unlock Deck
Unlock for access to all 101 flashcards in this deck.
Unlock Deck
k this deck
20
Which of the following methods is efficient in computing the integral 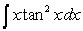 ?
?
A) Substitution Method with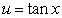
B) Integration by Parts with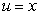 and
and 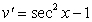
C) Integration by Parts with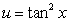 and
and 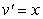
D) Integration by Parts with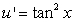 and
and 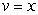
E) None of the techniques covered so far is efficient.
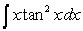 ?
?A) Substitution Method with
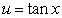
B) Integration by Parts with
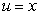 and
and 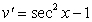
C) Integration by Parts with
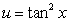 and
and 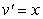
D) Integration by Parts with
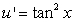 and
and 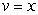
E) None of the techniques covered so far is efficient.

Unlock Deck
Unlock for access to all 101 flashcards in this deck.
Unlock Deck
k this deck
21
Use the substitution 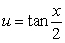 and the identities
and the identities 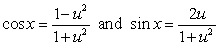 to evaluate the integral
to evaluate the integral 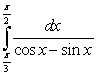 .
.
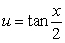 and the identities
and the identities 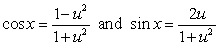 to evaluate the integral
to evaluate the integral 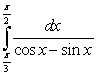 .
.
Unlock Deck
Unlock for access to all 101 flashcards in this deck.
Unlock Deck
k this deck
22
Use substitution and reduction formulas to evaluate the integral 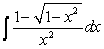 .
.
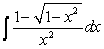 .
.
Unlock Deck
Unlock for access to all 101 flashcards in this deck.
Unlock Deck
k this deck
23
Evaluate the integral 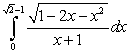 .
.
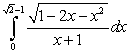 .
.
Unlock Deck
Unlock for access to all 101 flashcards in this deck.
Unlock Deck
k this deck
24
Evaluate the following integral using trigonometric identities and reduction formulas. 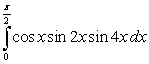
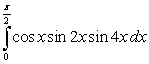

Unlock Deck
Unlock for access to all 101 flashcards in this deck.
Unlock Deck
k this deck
25
Evaluate the following integral using trigonometric identities and reduction formulas. 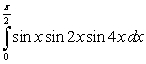
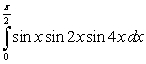

Unlock Deck
Unlock for access to all 101 flashcards in this deck.
Unlock Deck
k this deck
26
Use the substitution 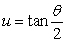 and the identity
and the identity 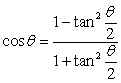 to evaluate the integral
to evaluate the integral 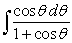 .
.
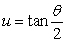 and the identity
and the identity 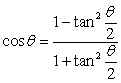 to evaluate the integral
to evaluate the integral 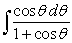 .
.
Unlock Deck
Unlock for access to all 101 flashcards in this deck.
Unlock Deck
k this deck
27
Evaluate the integral 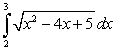 .
.
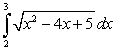 .
.
Unlock Deck
Unlock for access to all 101 flashcards in this deck.
Unlock Deck
k this deck
28
Evaluate the integral 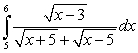 .
.
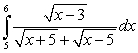 .
.
Unlock Deck
Unlock for access to all 101 flashcards in this deck.
Unlock Deck
k this deck
29
Evaluate the integral 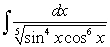 .
.
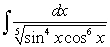 .
.
Unlock Deck
Unlock for access to all 101 flashcards in this deck.
Unlock Deck
k this deck
30
Calculate the following integral using reduction formulas as necessary. 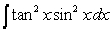
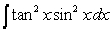

Unlock Deck
Unlock for access to all 101 flashcards in this deck.
Unlock Deck
k this deck
31
Evaluate the integral 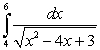 .
.
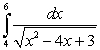 .
.
Unlock Deck
Unlock for access to all 101 flashcards in this deck.
Unlock Deck
k this deck
32
Evaluate the integral 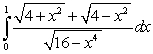 .
.
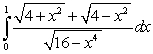 .
.
Unlock Deck
Unlock for access to all 101 flashcards in this deck.
Unlock Deck
k this deck
33
Evaluate the integral 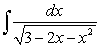 .
.
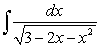 .
.
Unlock Deck
Unlock for access to all 101 flashcards in this deck.
Unlock Deck
k this deck
34
Evaluate the integral 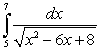 .
.
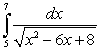 .
.
Unlock Deck
Unlock for access to all 101 flashcards in this deck.
Unlock Deck
k this deck
35
Calculate the following integrals using the reduction formulas when necessary.
A)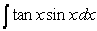
B)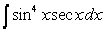
A)
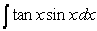
B)
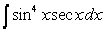

Unlock Deck
Unlock for access to all 101 flashcards in this deck.
Unlock Deck
k this deck
36
Evaluate the integral 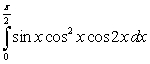 .
.
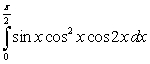 .
.
Unlock Deck
Unlock for access to all 101 flashcards in this deck.
Unlock Deck
k this deck
37
Evaluate the integral 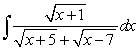 .
.
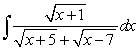 .
.
Unlock Deck
Unlock for access to all 101 flashcards in this deck.
Unlock Deck
k this deck
38
Evaluate the integral 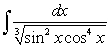 .
.
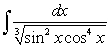 .
.
Unlock Deck
Unlock for access to all 101 flashcards in this deck.
Unlock Deck
k this deck
39
Evaluate the integral 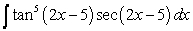 .
.
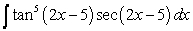 .
.
Unlock Deck
Unlock for access to all 101 flashcards in this deck.
Unlock Deck
k this deck
40
Calculate the integral 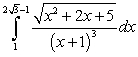 .
.
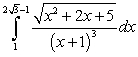 .
.
Unlock Deck
Unlock for access to all 101 flashcards in this deck.
Unlock Deck
k this deck
41
Evaluate the integral 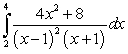 .
.
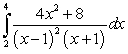 .
.
Unlock Deck
Unlock for access to all 101 flashcards in this deck.
Unlock Deck
k this deck
42
Evaluate the integral 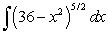 .
.
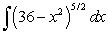 .
.
Unlock Deck
Unlock for access to all 101 flashcards in this deck.
Unlock Deck
k this deck
43
Evaluate the integral 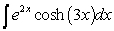 .
.
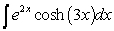 .
.
Unlock Deck
Unlock for access to all 101 flashcards in this deck.
Unlock Deck
k this deck
44
The partial fraction decomposition of 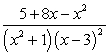 is:
is:
A) .
.
B)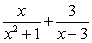 .
.
C)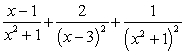 .
.
D)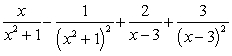 .
.
E)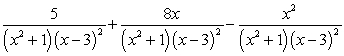 .
.
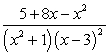 is:
is:A)
 .
.B)
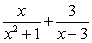 .
.C)
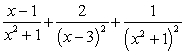 .
.D)
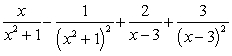 .
.E)
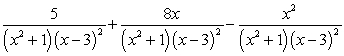 .
.
Unlock Deck
Unlock for access to all 101 flashcards in this deck.
Unlock Deck
k this deck
45
Evaluate the integral 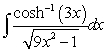 .
.
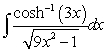 .
.
Unlock Deck
Unlock for access to all 101 flashcards in this deck.
Unlock Deck
k this deck
46
The partial fraction decomposition of 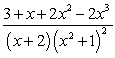 is:
is:
A)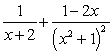 .
.
B)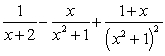 .
.
C)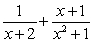 .
.
D)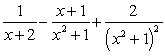 .
.
E)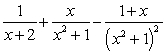 .
.
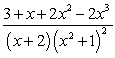 is:
is:A)
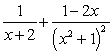 .
.B)
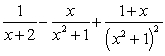 .
.C)
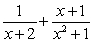 .
.D)
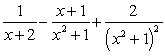 .
.E)
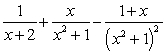 .
.
Unlock Deck
Unlock for access to all 101 flashcards in this deck.
Unlock Deck
k this deck
47
Evaluate the integral 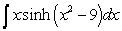 .
.
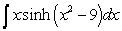 .
.
Unlock Deck
Unlock for access to all 101 flashcards in this deck.
Unlock Deck
k this deck
48
Calculate the following integral in terms of inverse hyperbolic functions. 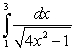
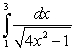

Unlock Deck
Unlock for access to all 101 flashcards in this deck.
Unlock Deck
k this deck
49
Evaluate the integral 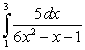 .
.
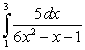 .
.
Unlock Deck
Unlock for access to all 101 flashcards in this deck.
Unlock Deck
k this deck
50
Use the substitution 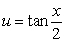 and the identities
and the identities 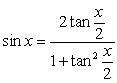 and
and 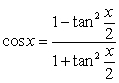 to rewrite the following integrand as a rational function and evaluate it.
to rewrite the following integrand as a rational function and evaluate it. 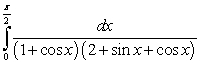
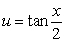 and the identities
and the identities 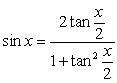 and
and 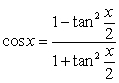 to rewrite the following integrand as a rational function and evaluate it.
to rewrite the following integrand as a rational function and evaluate it. 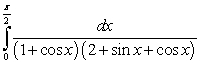

Unlock Deck
Unlock for access to all 101 flashcards in this deck.
Unlock Deck
k this deck
51
Evaluate the integral 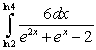 .
.
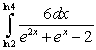 .
.
Unlock Deck
Unlock for access to all 101 flashcards in this deck.
Unlock Deck
k this deck
52
The partial fraction decomposition of 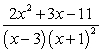 is:
is:
A)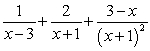 .
.
B)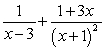 .
.
C)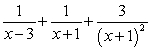 .
.
D)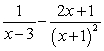 .
.
E)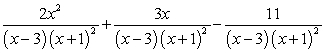 .
.
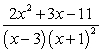 is:
is:A)
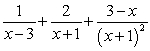 .
.B)
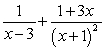 .
.C)
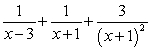 .
.D)
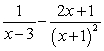 .
.E)
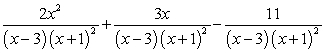 .
.
Unlock Deck
Unlock for access to all 101 flashcards in this deck.
Unlock Deck
k this deck
53
Evaluate the following integrals.
A)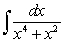
B)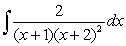
A)
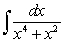
B)
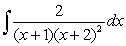

Unlock Deck
Unlock for access to all 101 flashcards in this deck.
Unlock Deck
k this deck
54
Evaluate the integral 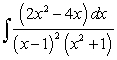 .
.
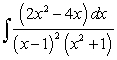 .
.
Unlock Deck
Unlock for access to all 101 flashcards in this deck.
Unlock Deck
k this deck
55
Evaluate the integral 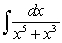 .
.
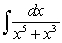 .
.
Unlock Deck
Unlock for access to all 101 flashcards in this deck.
Unlock Deck
k this deck
56
Calculate the following integral in terms of inverse hyperbolic functions. 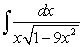
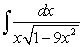

Unlock Deck
Unlock for access to all 101 flashcards in this deck.
Unlock Deck
k this deck
57
The partial fraction decomposition of 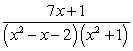 is:
is:
A)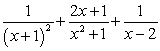 .
.
B)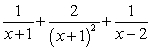 .
.
C)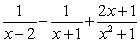 .
.
D)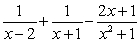 .
.
E)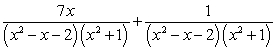 .
.
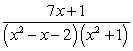 is:
is:A)
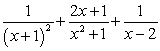 .
.B)
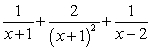 .
.C)
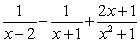 .
.D)
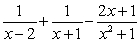 .
.E)
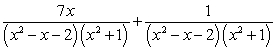 .
.
Unlock Deck
Unlock for access to all 101 flashcards in this deck.
Unlock Deck
k this deck
58
Evaluate the following integrals.
A)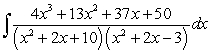
B)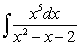
A)
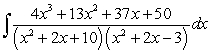
B)
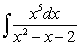

Unlock Deck
Unlock for access to all 101 flashcards in this deck.
Unlock Deck
k this deck
59
Evaluate 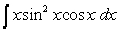 .
.
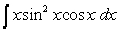 .
.
Unlock Deck
Unlock for access to all 101 flashcards in this deck.
Unlock Deck
k this deck
60
Use the substitution 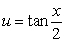 and the identities
and the identities 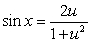 and
and 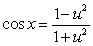 to evaluate the integral
to evaluate the integral 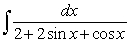 .
.
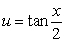 and the identities
and the identities 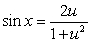 and
and 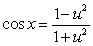 to evaluate the integral
to evaluate the integral 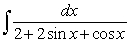 .
.
Unlock Deck
Unlock for access to all 101 flashcards in this deck.
Unlock Deck
k this deck
61
The time between customers at a checkout line is a random variable with exponential density. There is a 60% probability of waiting 1 min or more between customers. What is the average time between customers?

Unlock Deck
Unlock for access to all 101 flashcards in this deck.
Unlock Deck
k this deck
62
Which two of the following integrals converge?
A)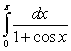
B)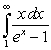
C)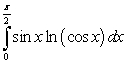
D)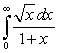
A)
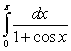
B)
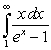
C)
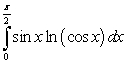
D)
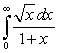

Unlock Deck
Unlock for access to all 101 flashcards in this deck.
Unlock Deck
k this deck
63
Compute the integral 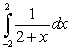 ..
..
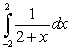 ..
..
Unlock Deck
Unlock for access to all 101 flashcards in this deck.
Unlock Deck
k this deck
64
Evaluate 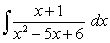 .
.
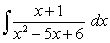 .
.
Unlock Deck
Unlock for access to all 101 flashcards in this deck.
Unlock Deck
k this deck
65
The integral 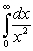 :
:
A) diverges since the power of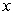 is not less than 1.
is not less than 1.
B) converges since the power of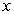 is greater than 1.
is greater than 1.
C) diverges since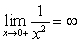 .
.
D) converges since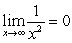 .
.
E) none of the above
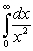 :
:A) diverges since the power of
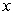 is not less than 1.
is not less than 1.B) converges since the power of
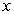 is greater than 1.
is greater than 1.C) diverges since
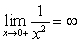 .
.D) converges since
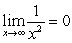 .
.E) none of the above

Unlock Deck
Unlock for access to all 101 flashcards in this deck.
Unlock Deck
k this deck
66
Which of the following integrals converges?
A)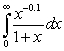
B)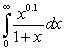
C)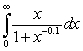
D)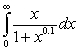
E)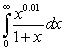
A)
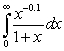
B)
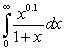
C)
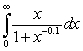
D)
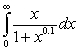
E)
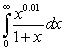

Unlock Deck
Unlock for access to all 101 flashcards in this deck.
Unlock Deck
k this deck
67
Evaluate the following improper integrals, if they exist.
A)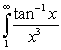
B)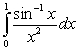
A)
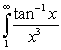
B)
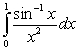

Unlock Deck
Unlock for access to all 101 flashcards in this deck.
Unlock Deck
k this deck
68
Verify that 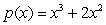 is a probability density function on
is a probability density function on 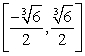 and calculate its mean value.
and calculate its mean value.
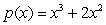 is a probability density function on
is a probability density function on 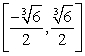 and calculate its mean value.
and calculate its mean value.
Unlock Deck
Unlock for access to all 101 flashcards in this deck.
Unlock Deck
k this deck
69
Which of the following integrals converges?
A)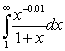
B)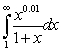
C)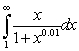
D)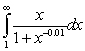
E) none of the above.
A)
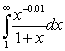
B)
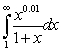
C)
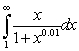
D)
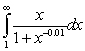
E) none of the above.

Unlock Deck
Unlock for access to all 101 flashcards in this deck.
Unlock Deck
k this deck
70
Evaluate 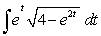 .
.
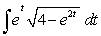 .
.
Unlock Deck
Unlock for access to all 101 flashcards in this deck.
Unlock Deck
k this deck
71
To show that 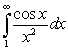 converges, we should use:
converges, we should use:
A) the Comparison Test and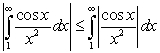 .
.
B) the Comparison Test and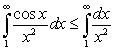 .
.
C) evaluation of the integral.
D) No method can be used since the function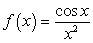 is not non-negative.
is not non-negative.
E) none of the above.
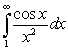 converges, we should use:
converges, we should use:A) the Comparison Test and
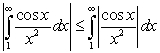 .
.B) the Comparison Test and
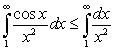 .
.C) evaluation of the integral.
D) No method can be used since the function
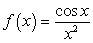 is not non-negative.
is not non-negative.E) none of the above.

Unlock Deck
Unlock for access to all 101 flashcards in this deck.
Unlock Deck
k this deck
72
Evaluate the following improper integrals.
A)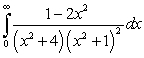
B)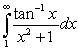
A)
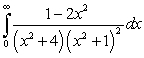
B)
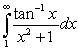

Unlock Deck
Unlock for access to all 101 flashcards in this deck.
Unlock Deck
k this deck
73
Find a constant 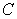 such that
such that 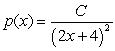 is a probability density function on the interval
is a probability density function on the interval 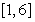 and compute the probability
and compute the probability 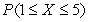 .
.
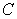 such that
such that 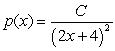 is a probability density function on the interval
is a probability density function on the interval 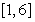 and compute the probability
and compute the probability 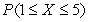 .
.
Unlock Deck
Unlock for access to all 101 flashcards in this deck.
Unlock Deck
k this deck
74
Compute the integral 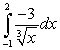 ..
..
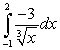 ..
..
Unlock Deck
Unlock for access to all 101 flashcards in this deck.
Unlock Deck
k this deck
75
To show that 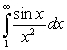 converges, we should use:
converges, we should use:
A) the inequality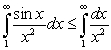 and the Comparison Test.
and the Comparison Test.
B) the inequality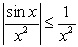 and the Comparison Test.
and the Comparison Test.
C) evaluation of the integral.
D) No method can be used, since the function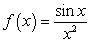 is not non-negative.
is not non-negative.
E) none of the above.
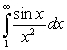 converges, we should use:
converges, we should use:A) the inequality
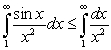 and the Comparison Test.
and the Comparison Test.B) the inequality
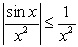 and the Comparison Test.
and the Comparison Test.C) evaluation of the integral.
D) No method can be used, since the function
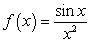 is not non-negative.
is not non-negative.E) none of the above.

Unlock Deck
Unlock for access to all 101 flashcards in this deck.
Unlock Deck
k this deck
76
Evaluate the following improper integrals.
A)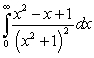
B)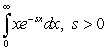
A)
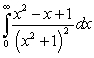
B)
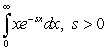

Unlock Deck
Unlock for access to all 101 flashcards in this deck.
Unlock Deck
k this deck
77
Evaluate the following improper integrals.
A)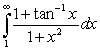
B)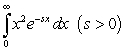
A)
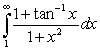
B)
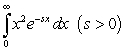

Unlock Deck
Unlock for access to all 101 flashcards in this deck.
Unlock Deck
k this deck
78
Evaluate 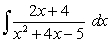 .
.
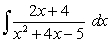 .
.
Unlock Deck
Unlock for access to all 101 flashcards in this deck.
Unlock Deck
k this deck
79
To show that 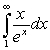 converges, we should use:
converges, we should use:
A) the inequality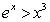 and the Comparison Test.
and the Comparison Test.
B) the inequality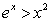 and the Comparison Test.
and the Comparison Test.
C) evaluation of the integral.
D) the inequality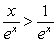 and the Comparison Test.
and the Comparison Test.
E) none of the above.
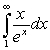 converges, we should use:
converges, we should use:A) the inequality
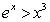 and the Comparison Test.
and the Comparison Test.B) the inequality
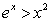 and the Comparison Test.
and the Comparison Test.C) evaluation of the integral.
D) the inequality
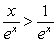 and the Comparison Test.
and the Comparison Test.E) none of the above.

Unlock Deck
Unlock for access to all 101 flashcards in this deck.
Unlock Deck
k this deck
80
Evaluate 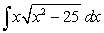 .
.
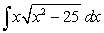 .
.
Unlock Deck
Unlock for access to all 101 flashcards in this deck.
Unlock Deck
k this deck


