Deck 9: Further Applications of the Integral and Taylor Polynomials
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/100
Play
Full screen (f)
Deck 9: Further Applications of the Integral and Taylor Polynomials
1
Approximate the arc length of the curve 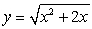 over the interval
over the interval 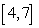 using Simpson's Rule
using Simpson's Rule  .
.
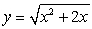 over the interval
over the interval 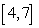 using Simpson's Rule
using Simpson's Rule 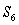 .
.4.27
2
Let  be the solid obtained by revolving the infinite graph of
be the solid obtained by revolving the infinite graph of 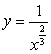 about the x-axis for
about the x-axis for 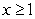 .
. 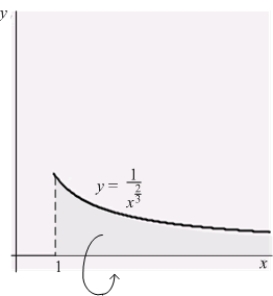 Which of the following statements is correct?
Which of the following statements is correct?
A) has infinite volume and finite surface area.
has infinite volume and finite surface area.
B) has finite volume and infinite surface area.
has finite volume and infinite surface area.
C)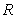 has finite volume and finite surface area.
has finite volume and finite surface area.
D)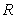 has infinite volume and infinite surface area.
has infinite volume and infinite surface area.
E) None of the above is correct.
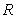 be the solid obtained by revolving the infinite graph of
be the solid obtained by revolving the infinite graph of 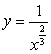 about the x-axis for
about the x-axis for 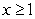 .
.  Which of the following statements is correct?
Which of the following statements is correct?A)
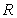 has infinite volume and finite surface area.
has infinite volume and finite surface area.B)
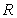 has finite volume and infinite surface area.
has finite volume and infinite surface area.C)
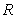 has finite volume and finite surface area.
has finite volume and finite surface area.D)
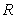 has infinite volume and infinite surface area.
has infinite volume and infinite surface area.E) None of the above is correct.
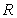 has finite volume and infinite surface area.
has finite volume and infinite surface area. 3
Approximate the arc length of the curve 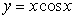 over the interval
over the interval 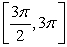 using the Trapezoidal Rule
using the Trapezoidal Rule 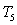 .
.
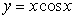 over the interval
over the interval 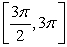 using the Trapezoidal Rule
using the Trapezoidal Rule 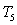 .
.21.956
4
Compute the surface area of revolution of 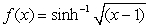 about the x-axis over the interval
about the x-axis over the interval 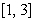 .
.
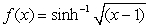 about the x-axis over the interval
about the x-axis over the interval 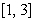 .
.
Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
5
Calculate the arc length of 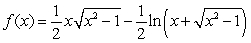 over the interval
over the interval 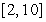 .
.
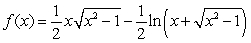 over the interval
over the interval 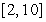 .
.
Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
6
Calculate the arc length of the curve 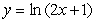 over the interval
over the interval 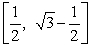 .
.
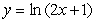 over the interval
over the interval 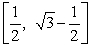 .
.
Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
7
Compute the area of the surface obtained by rotating the graph of 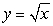 ,
,  about the x-axis.
about the x-axis. 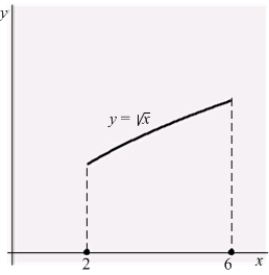
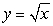 ,
, 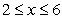 about the x-axis.
about the x-axis. 

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
8
Compute the surface area of revolution of 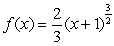 about the x-axis over the interval
about the x-axis over the interval 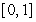 .
.
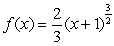 about the x-axis over the interval
about the x-axis over the interval 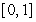 .
.
Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
9
Compute the surface area of revolution of 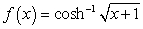 about the x-axis over the interval
about the x-axis over the interval 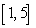 .
.
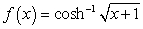 about the x-axis over the interval
about the x-axis over the interval 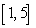 .
.
Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
10
Calculate the arc length of the curve 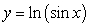 over the interval
over the interval 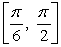 .
.
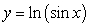 over the interval
over the interval 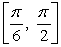 .
.
Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
11
Compute the arc length of 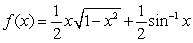 for
for 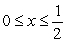 .
.
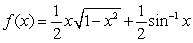 for
for 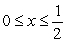 .
.
Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
12
Compute the surface area of revolution of 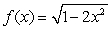 about the x-axis over the interval
about the x-axis over the interval 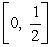 .
.
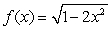 about the x-axis over the interval
about the x-axis over the interval 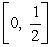 .
.
Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
13
Use implicit differentiation to compute the surface area of revolution about the x-axis of the part of the astroid 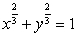 in the first quadrant.
in the first quadrant. 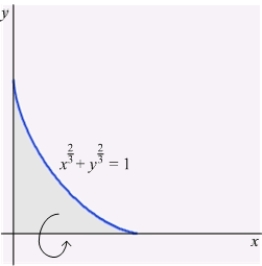
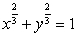 in the first quadrant.
in the first quadrant. 

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
14
Find the area of the surface obtained by rotating the graph of 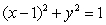 ,
,  about the x-axis.
about the x-axis. 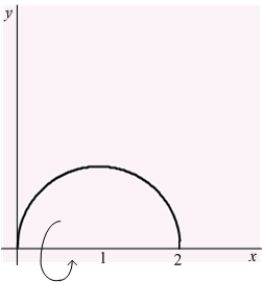
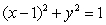 ,
, 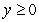 about the x-axis.
about the x-axis. 

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
15
Calculate the arc length of ![Calculate the arc length of over the interval [1, 5].](https://storage.examlex.com/TB5596/11eaa655_3af6_1d21_a696_970bec6b9115_TB5596_11.jpg) over the interval [1, 5].
over the interval [1, 5].
![Calculate the arc length of over the interval [1, 5].](https://storage.examlex.com/TB5596/11eaa655_3af6_1d21_a696_970bec6b9115_TB5596_11.jpg) over the interval [1, 5].
over the interval [1, 5].
Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
16
Let 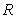 be the solid obtained by revolving the infinite graph of
be the solid obtained by revolving the infinite graph of 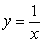 about the x-axis for
about the x-axis for 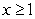 .
. 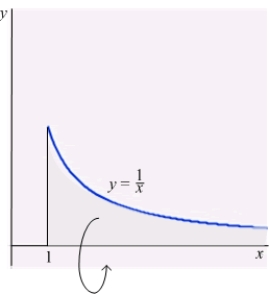 Which of the following statements is correct?
Which of the following statements is correct?
A) has finite volume and finite surface area.
has finite volume and finite surface area.
B) has finite surface area and infinite volume.
has finite surface area and infinite volume.
C) has finite volume and infinite surface area.
has finite volume and infinite surface area.
D)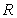 has infinite volume and infinite surface area.
has infinite volume and infinite surface area.
E) None of the above is correct.
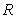 be the solid obtained by revolving the infinite graph of
be the solid obtained by revolving the infinite graph of 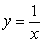 about the x-axis for
about the x-axis for 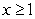 .
.  Which of the following statements is correct?
Which of the following statements is correct?A)
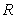 has finite volume and finite surface area.
has finite volume and finite surface area.B)
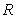 has finite surface area and infinite volume.
has finite surface area and infinite volume.C)
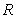 has finite volume and infinite surface area.
has finite volume and infinite surface area.D)
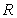 has infinite volume and infinite surface area.
has infinite volume and infinite surface area.E) None of the above is correct.

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
17
Compute the surface area of revolution of 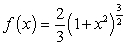 about the x-axis over the interval
about the x-axis over the interval 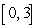 .
.
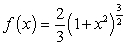 about the x-axis over the interval
about the x-axis over the interval 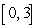 .
.
Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
18
Compute the arc length of ![Compute the arc length of over the interval [0, 2].](https://storage.examlex.com/TB5596/11eaa655_3af6_6a4a_a696_81853635175a_TB5596_11.jpg) over the interval [0, 2].
over the interval [0, 2].
![Compute the arc length of over the interval [0, 2].](https://storage.examlex.com/TB5596/11eaa655_3af6_6a4a_a696_81853635175a_TB5596_11.jpg) over the interval [0, 2].
over the interval [0, 2].
Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
19
Find the area of the surface obtained by rotating the loop 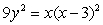 ,
, 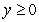 ,
, 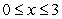 about the x-axis.
about the x-axis.
Use implicit differentiation to facilitate your computations.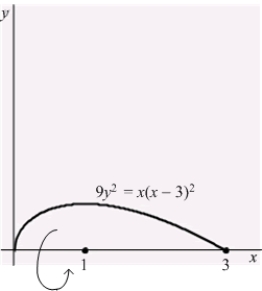
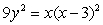 ,
, 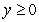 ,
, 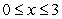 about the x-axis.
about the x-axis.Use implicit differentiation to facilitate your computations.


Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
20
Calculate the arc length of 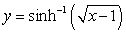 over the interval
over the interval 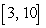 .
.
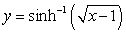 over the interval
over the interval 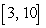 .
.
Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
21
The plate shown in the figure, determined by the region enclosed by the graphs of 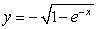 ,
, 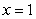 , and
, and 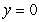 , is submerged vertically in a fluid with density
, is submerged vertically in a fluid with density 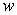 so that its top edge is level with the surface of the fluid. Find the force on a side of the plate if
so that its top edge is level with the surface of the fluid. Find the force on a side of the plate if 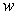 is given in terms of weight per unit volume.
is given in terms of weight per unit volume. 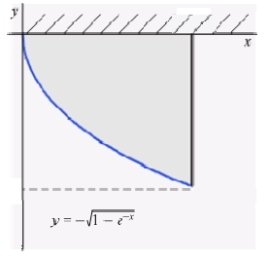
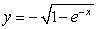 ,
, 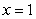 , and
, and 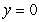 , is submerged vertically in a fluid with density
, is submerged vertically in a fluid with density 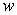 so that its top edge is level with the surface of the fluid. Find the force on a side of the plate if
so that its top edge is level with the surface of the fluid. Find the force on a side of the plate if 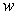 is given in terms of weight per unit volume.
is given in terms of weight per unit volume. 

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
22
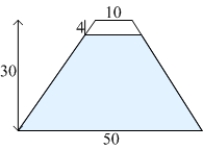
The face of a dam is an isosceles trapezoid of height 30 ft and bases 10 ft and 50 ft. The dam is oriented vertically with the larger base at the bottom. Find the force on the dam if the water level is 4 ft below the top of the dam. (The density of the water is 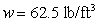 .)
.) 
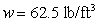 .)
.) 

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
23
The plate shown in the figure is submerged in water so that its top is level with the surface of the water. Find the fluid pressure on a side of the plate. (The density of water is 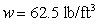 .)
.) 
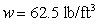 .)
.) 

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
24
An infinite plate shown in the figure below, bounded by the graphs of 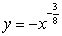 and
and 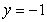 and the y-axis, is submerged vertically in water, with its top
and the y-axis, is submerged vertically in water, with its top 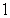 ft below the water surface.
ft below the water surface.
Calculate the fluid force on a side of the plate. (The density of water is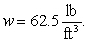 )
) 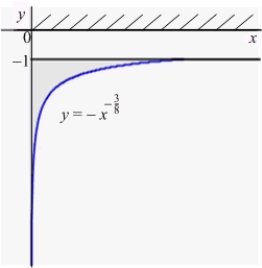
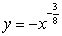 and
and 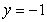 and the y-axis, is submerged vertically in water, with its top
and the y-axis, is submerged vertically in water, with its top 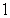 ft below the water surface.
ft below the water surface.Calculate the fluid force on a side of the plate. (The density of water is
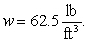 )
) 

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
25
The plate shown in the figure, enclosed by the curves 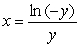 ,
, 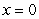 , and
, and 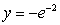 , is submerged vertically in a fluid with density
, is submerged vertically in a fluid with density 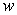 so that its top is at a depth of
so that its top is at a depth of 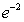 . Find the fluid pressure on a side of the plate if
. Find the fluid pressure on a side of the plate if 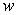 is given in terms of weight per unit volume.
is given in terms of weight per unit volume. 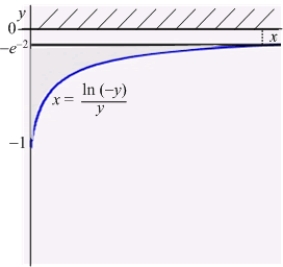
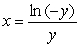 ,
, 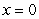 , and
, and 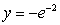 , is submerged vertically in a fluid with density
, is submerged vertically in a fluid with density 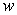 so that its top is at a depth of
so that its top is at a depth of 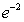 . Find the fluid pressure on a side of the plate if
. Find the fluid pressure on a side of the plate if 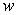 is given in terms of weight per unit volume.
is given in terms of weight per unit volume. 

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
26
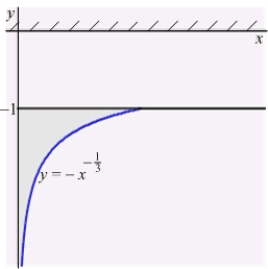
An infinite plate shown in the figure below, bounded by the graphs of 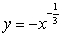 and
and 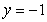 and the y-axis, is submerged vertically in water, with its top
and the y-axis, is submerged vertically in water, with its top 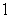 ft below the water surface.
ft below the water surface.
Calculate the fluid force on a side of the plate. (The density of water is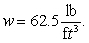 )
) 
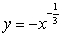 and
and 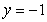 and the y-axis, is submerged vertically in water, with its top
and the y-axis, is submerged vertically in water, with its top 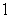 ft below the water surface.
ft below the water surface.Calculate the fluid force on a side of the plate. (The density of water is
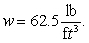 )
) 

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
27
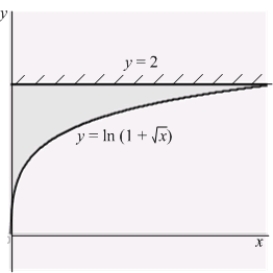
A thin plate shown in the figure below, bounded by the curves 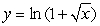 ,
, 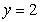 , and
, and 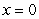 is submerged vertically in water, with its top level with the water's surface. Calculate the fluid force on a side of the plate.
is submerged vertically in water, with its top level with the water's surface. Calculate the fluid force on a side of the plate.
(The density of water is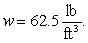 )
) 
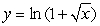 ,
, 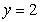 , and
, and 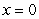 is submerged vertically in water, with its top level with the water's surface. Calculate the fluid force on a side of the plate.
is submerged vertically in water, with its top level with the water's surface. Calculate the fluid force on a side of the plate.(The density of water is
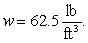 )
) 

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
28
Calculate the arc length of 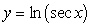 over the interval
over the interval 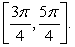
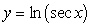 over the interval
over the interval 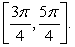

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
29
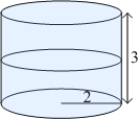
A water tank is a cylinder 4 ft in diameter, standing on its base. If water fills the tank to a depth of 3 ft, what is the magnitude of the force exerted on the side of the tank? (The density of the water is 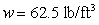 .)
.) 
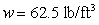 .)
.) 

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
30
An infinite plate shown in the figure below, bounded by the graphs of 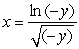 and
and 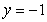 and the two axes, is submerged vertically in a fluid with density
and the two axes, is submerged vertically in a fluid with density 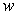 in kilograms per cubic meter; its top is level with the fluid surface.
in kilograms per cubic meter; its top is level with the fluid surface.
Calculate the fluid force on a side of the plate and write the answer in terms of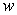 and
and 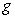 .
. 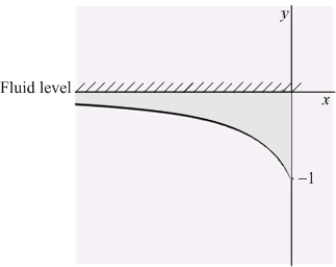
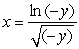 and
and 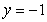 and the two axes, is submerged vertically in a fluid with density
and the two axes, is submerged vertically in a fluid with density 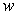 in kilograms per cubic meter; its top is level with the fluid surface.
in kilograms per cubic meter; its top is level with the fluid surface.Calculate the fluid force on a side of the plate and write the answer in terms of
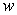 and
and 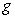 .
. 

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
31
The plate shown in the figure below, bounded by the graph of 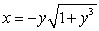 and the
and the
y-axis, is submerged vertically in a fluid with density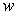 so that its top is level with the fluid surface.
so that its top is level with the fluid surface.
Find the fluid pressure on a side of the plate if is given in terms of weight per unit volume.
is given in terms of weight per unit volume. 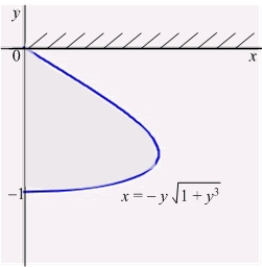
 and the
and they-axis, is submerged vertically in a fluid with density
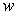 so that its top is level with the fluid surface.
so that its top is level with the fluid surface.Find the fluid pressure on a side of the plate if
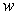 is given in terms of weight per unit volume.
is given in terms of weight per unit volume. 

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
32
The plate determined by the region between the graphs of 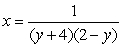 and
and 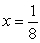 is submerged in a fluid with density
is submerged in a fluid with density 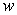 , with its top touching the surface of the fluid.
, with its top touching the surface of the fluid.
Find the fluid pressure on a side of the plate if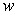 is given in terms of weight per unit volume.
is given in terms of weight per unit volume. 
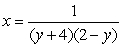 and
and 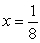 is submerged in a fluid with density
is submerged in a fluid with density 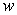 , with its top touching the surface of the fluid.
, with its top touching the surface of the fluid.Find the fluid pressure on a side of the plate if
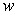 is given in terms of weight per unit volume.
is given in terms of weight per unit volume. 

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
33
Compute the arc length of 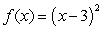 for
for 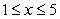 .
.
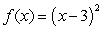 for
for 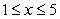 .
.
Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
34
A thin plate shown in the figure, bounded by the graphs 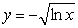 and
and 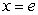 and the x-axis, is submerged vertically in a fluid of density
and the x-axis, is submerged vertically in a fluid of density  so that its top is level with the fluid surface.
so that its top is level with the fluid surface.
Calculate the fluid pressure on a side of the plate if is given in terms of weight per unit volume.
is given in terms of weight per unit volume. 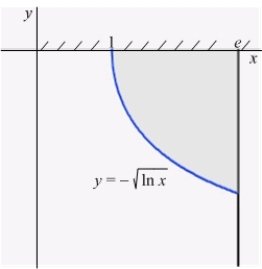
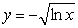 and
and 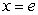 and the x-axis, is submerged vertically in a fluid of density
and the x-axis, is submerged vertically in a fluid of density 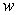 so that its top is level with the fluid surface.
so that its top is level with the fluid surface.Calculate the fluid pressure on a side of the plate if
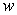 is given in terms of weight per unit volume.
is given in terms of weight per unit volume. 

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
35
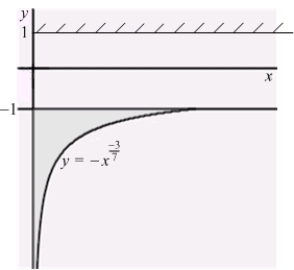
An infinite plate shown in the figure below, bounded by the graphs of 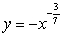 ,
, 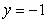 , and the y-axis, is submerged vertically in water, with its top
, and the y-axis, is submerged vertically in water, with its top 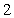 ft below the water surface. Calculate the fluid force on a side of the plate.
ft below the water surface. Calculate the fluid force on a side of the plate.
(The density of water is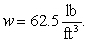 )
) 
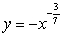 ,
, 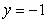 , and the y-axis, is submerged vertically in water, with its top
, and the y-axis, is submerged vertically in water, with its top 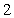 ft below the water surface. Calculate the fluid force on a side of the plate.
ft below the water surface. Calculate the fluid force on a side of the plate.(The density of water is
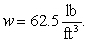 )
) 

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
36
Approximate the arc length of the curve 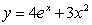 over the interval
over the interval 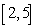 using Simpson's Rule
using Simpson's Rule  .
.
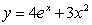 over the interval
over the interval 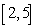 using Simpson's Rule
using Simpson's Rule 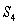 .
.
Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
37
Find the surface area of the ellipsoid obtained by rotating the ellipse 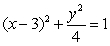 about the x-axis.
about the x-axis.
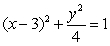 about the x-axis.
about the x-axis.
Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
38
A thin plate shown in the following figure is bounded by the graphs of 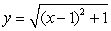 and
and 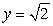 . The plate is submerged in a fluid with density
. The plate is submerged in a fluid with density 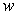 so that its top is level with the surface of the fluid.
so that its top is level with the surface of the fluid.
Calculate the fluid pressure on a side of the plate if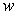 is given in terms of weight per unit volume.
is given in terms of weight per unit volume. 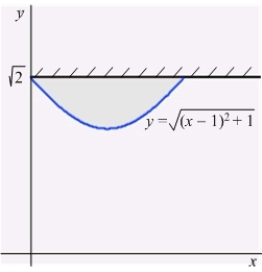
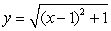 and
and 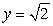 . The plate is submerged in a fluid with density
. The plate is submerged in a fluid with density 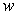 so that its top is level with the surface of the fluid.
so that its top is level with the surface of the fluid.Calculate the fluid pressure on a side of the plate if
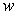 is given in terms of weight per unit volume.
is given in terms of weight per unit volume. 

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
39
Let 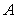 be the region shown in the figure below enclosed by the graph of
be the region shown in the figure below enclosed by the graph of 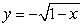 ,
,
the positive x-axis, and the negative y-axis.
Calculate the fluid force on a side of the plate in the shape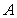 if the water surface is at
if the water surface is at 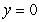 .
.
(The density of water is w =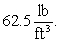 )
) 
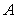 be the region shown in the figure below enclosed by the graph of
be the region shown in the figure below enclosed by the graph of 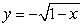 ,
,the positive x-axis, and the negative y-axis.
Calculate the fluid force on a side of the plate in the shape
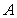 if the water surface is at
if the water surface is at 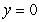 .
.(The density of water is w =
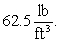 )
) 

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
40
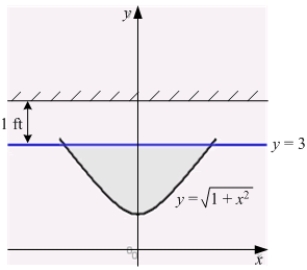
A thin plate shown in the figure below, bounded by the curves 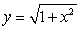 and
and 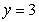 , is submerged vertically in water with its top
, is submerged vertically in water with its top 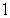 ft below the water surface. Calculate the fluid force on a side of the plate.
ft below the water surface. Calculate the fluid force on a side of the plate.
(The density of water is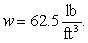 )
) 
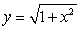 and
and 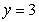 , is submerged vertically in water with its top
, is submerged vertically in water with its top 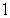 ft below the water surface. Calculate the fluid force on a side of the plate.
ft below the water surface. Calculate the fluid force on a side of the plate.(The density of water is
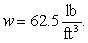 )
) 

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
41
A right triangle is submerged vertically in water so that the base is the part of the triangle which is closest to the surface. Suppose that the base of the triangle is 2 ft long, and the height is 6 ft. What is the fluid force on a side of the triangle if the base is 3 ft from the surface? (The density of water is 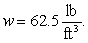 )
)
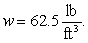 )
)
Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
42
Find the center of mass of the region enclosed by the graphs of 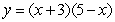 and
and 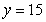 .
. 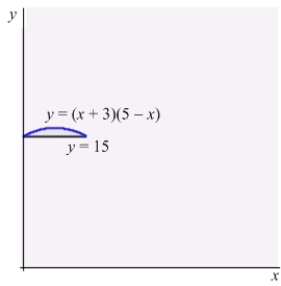
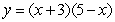 and
and 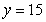 .
. 

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
43
Find the centroid of the shaded region in the following figure. 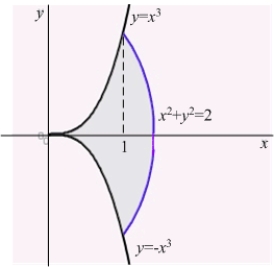


Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
44
An infinite plate occupying the region bounded by the functions 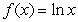 and
and 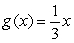 on the interval
on the interval 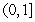 is submerged vertically so that the top of the plate is under 1.5 m of water. What is the fluid force on the side of the plate?
is submerged vertically so that the top of the plate is under 1.5 m of water. What is the fluid force on the side of the plate?
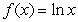 and
and 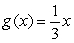 on the interval
on the interval  is submerged vertically so that the top of the plate is under 1.5 m of water. What is the fluid force on the side of the plate?
is submerged vertically so that the top of the plate is under 1.5 m of water. What is the fluid force on the side of the plate?
Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
45
A rectangular box with height 2 m, width 3 m, and length 4 m is submerged in a pool of water. The top of the box is 5 m below the surface of the water.
Compute the fluid force on one of the box sides with dimensions 4 m by 2 m.
Compute the fluid force on one of the box sides with dimensions 4 m by 2 m.

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
46
Find the centroid of the quarter ring shown in the figure below. 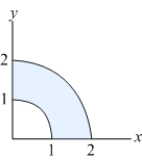


Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
47
Find the centroid of the shaded region in the figure below. 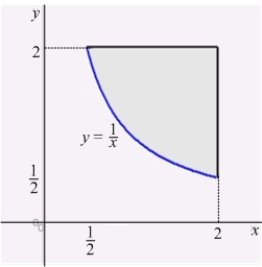


Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
48
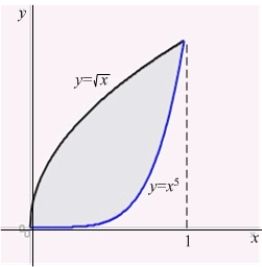
Find the centroid of the region enclosed by the curves 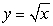 and
and 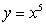 .
. 
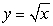 and
and 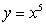 .
. 

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
49
A plate bounded by the functions 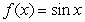 and
and 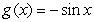 on the interval
on the interval 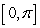 is submerged vertically so that the top of the plate is under 1 m of water. What is the fluid force on the side of the plate?
is submerged vertically so that the top of the plate is under 1 m of water. What is the fluid force on the side of the plate?
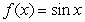 and
and 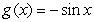 on the interval
on the interval 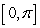 is submerged vertically so that the top of the plate is under 1 m of water. What is the fluid force on the side of the plate?
is submerged vertically so that the top of the plate is under 1 m of water. What is the fluid force on the side of the plate?
Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
50
A plate occupying the region bounded by the functions 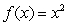 and
and 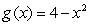 is submerged vertically so that the top of the plate is under 2 m of water. What is the fluid force on the side of the plate?
is submerged vertically so that the top of the plate is under 2 m of water. What is the fluid force on the side of the plate?
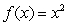 and
and 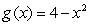 is submerged vertically so that the top of the plate is under 2 m of water. What is the fluid force on the side of the plate?
is submerged vertically so that the top of the plate is under 2 m of water. What is the fluid force on the side of the plate?
Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
51
A plate bounded by the functions 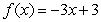 ,
, 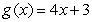 ,
, 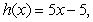 and
and 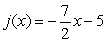 is submerged vertically so that the top of the plate is under 4 m of water. What is the fluid force on the side of the plate?
is submerged vertically so that the top of the plate is under 4 m of water. What is the fluid force on the side of the plate?
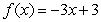 ,
, 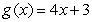 ,
, 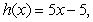 and
and 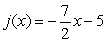 is submerged vertically so that the top of the plate is under 4 m of water. What is the fluid force on the side of the plate?
is submerged vertically so that the top of the plate is under 4 m of water. What is the fluid force on the side of the plate?
Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
52
Use additivity of moments to find the center of mass of the region consisting of a semicircle on top of an isosceles trapezoid of height 1 and bases 2 and 4, as shown below. 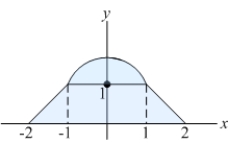


Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
53
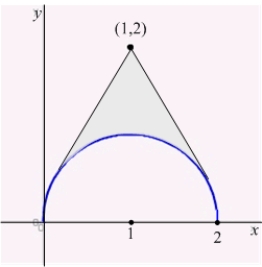
Find the centroid of the region in the figure below enclosed by the circle 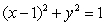 and the two tangents to the circle intersecting at the point
and the two tangents to the circle intersecting at the point 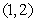 .
. 
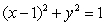 and the two tangents to the circle intersecting at the point
and the two tangents to the circle intersecting at the point 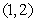 .
. 

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
54
Find the centroid of the region lying between the graphs of 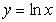 and
and 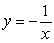 over the interval
over the interval 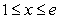 .
. 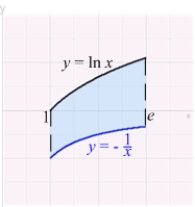

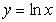 and
and 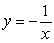 over the interval
over the interval 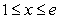 .
. 


Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
55
The centroid of the region enclosed by the graphs of 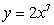 and
and 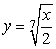 lies on the line
lies on the line
A)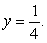
B)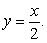
C)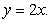
D)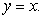
E)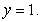
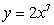 and
and 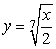 lies on the line
lies on the lineA)
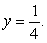
B)
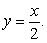
C)
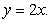
D)
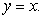
E)
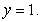

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
56
Let 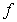 be an invertible function such that
be an invertible function such that 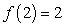 and
and 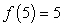 . Let
. Let 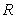 be the region enclosed by the graphs of
be the region enclosed by the graphs of 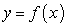 and
and 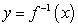 over the interval
over the interval 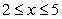 . The centroid of
. The centroid of 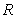 lies on
lies on
A) the line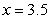 .
.
B) the line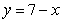 .
.
C) the line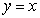 .
.
D) It depends on the function .
.
E) none of the above.
 be an invertible function such that
be an invertible function such that 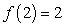 and
and 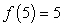 . Let
. Let 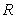 be the region enclosed by the graphs of
be the region enclosed by the graphs of 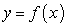 and
and 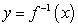 over the interval
over the interval 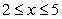 . The centroid of
. The centroid of 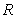 lies on
lies onA) the line
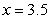 .
.B) the line
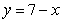 .
.C) the line
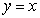 .
.D) It depends on the function
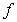 .
.E) none of the above.

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
57
A water tank is a rectangular tank with a square base of side length 4 ft and a height of 3 ft, standing on its base. If oil fills the tank to a depth of 2 ft, what is the magnitude of the force exerted on each of the vertical sides of the tank? (The density of the oil is 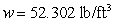 .)
.)
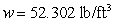 .)
.)
Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
58
A plate occupying the region bounded by the functions 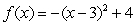 and
and 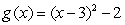 is submerged vertically so that the top of the plate is under 2 m of water. What is the fluid force on the side of the plate?
is submerged vertically so that the top of the plate is under 2 m of water. What is the fluid force on the side of the plate?
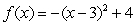 and
and 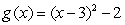 is submerged vertically so that the top of the plate is under 2 m of water. What is the fluid force on the side of the plate?
is submerged vertically so that the top of the plate is under 2 m of water. What is the fluid force on the side of the plate?
Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
59
A plate occupying the region bounded by the functions 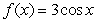 and
and 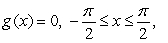 is submerged vertically so that the top of the plate is under 5 m of water. What is the fluid force on the side of the plate?
is submerged vertically so that the top of the plate is under 5 m of water. What is the fluid force on the side of the plate?
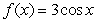 and
and 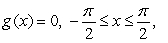 is submerged vertically so that the top of the plate is under 5 m of water. What is the fluid force on the side of the plate?
is submerged vertically so that the top of the plate is under 5 m of water. What is the fluid force on the side of the plate?
Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
60
Find the centroid of the shaded region in the figure below. 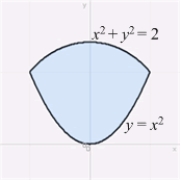


Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
61
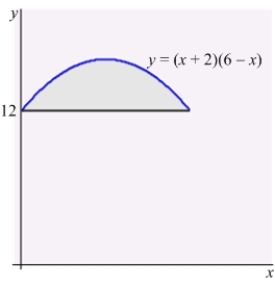
Find the center of mass of the region enclosed by the graphs of 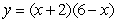 and
and 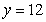 .
. 
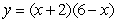 and
and 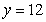 .
. 

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
62
Calculate the Taylor polynomial 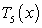 centered at
centered at 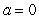 for
for 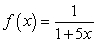 .
.
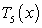 centered at
centered at 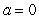 for
for 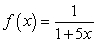 .
.
Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
63
Find the centroid of the region enclosed by the graphs 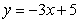 ,
, 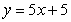 ,
, 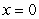 , and
, and 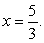
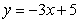 ,
, 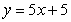 ,
, 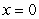 , and
, and 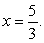

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
64
The quotient 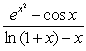 is equal to:
is equal to:
A)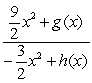 where
where 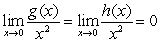
B)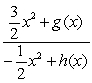 where
where 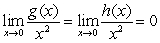
C)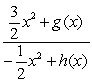 where
where 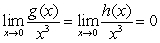
D)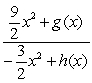 where
where 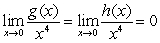
E) none of the above.
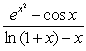 is equal to:
is equal to:A)
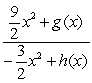 where
where 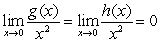
B)
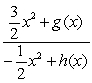 where
where 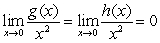
C)
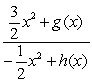 where
where 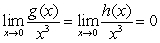
D)
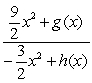 where
where 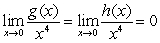
E) none of the above.

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
65
Let 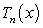 be the Taylor polynomial of
be the Taylor polynomial of 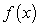 centered at
centered at 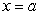 . Which of the following statements is correct?
. Which of the following statements is correct?
A)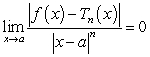
B)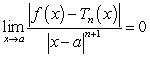
C)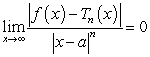
D)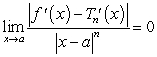
E) None of the above is correct.
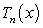 be the Taylor polynomial of
be the Taylor polynomial of 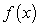 centered at
centered at 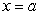 . Which of the following statements is correct?
. Which of the following statements is correct?A)
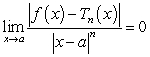
B)
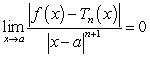
C)
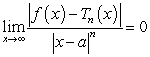
D)
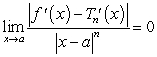
E) None of the above is correct.

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
66
Compute 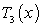 for
for 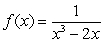 centered at
centered at 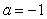 . Use the error bound to find the maximum possible size of error of
. Use the error bound to find the maximum possible size of error of 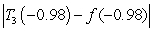 .
.
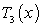 for
for 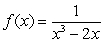 centered at
centered at 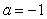 . Use the error bound to find the maximum possible size of error of
. Use the error bound to find the maximum possible size of error of 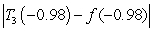 .
.
Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
67
Compute 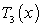 for
for 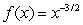 centered at
centered at 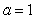 . Use the error bound to find the maximum possible size of error of
. Use the error bound to find the maximum possible size of error of 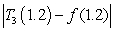 .
.
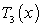 for
for 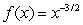 centered at
centered at 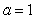 . Use the error bound to find the maximum possible size of error of
. Use the error bound to find the maximum possible size of error of 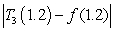 .
.
Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
68
Which of the following is a Maclaurin polynomial of 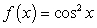 ?
?
A)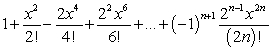
B)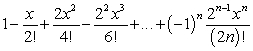
C)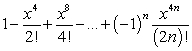
D)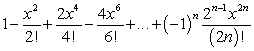
E)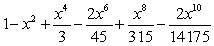
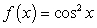 ?
?A)
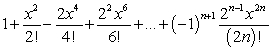
B)
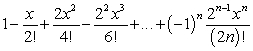
C)
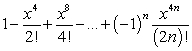
D)
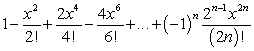
E)
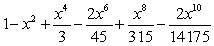

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
69
Find the centroid of the portion of the unit circle lying within the first three quadrants.

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
70
Find the centroid of the region enclosed by the graph of 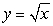 , the tangent to the graph at
, the tangent to the graph at 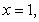 and the y-axis.
and the y-axis. 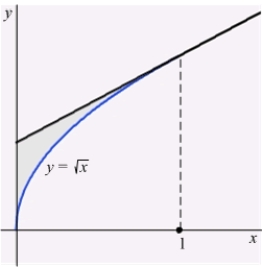
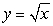 , the tangent to the graph at
, the tangent to the graph at 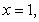 and the y-axis.
and the y-axis. 

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
71
Five particles of equal mass are located at 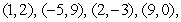 and
and 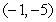 . Find the center of mass of the system.
. Find the center of mass of the system.
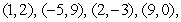 and
and 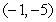 . Find the center of mass of the system.
. Find the center of mass of the system.
Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
72
Find the centroid of the shaded region in the figure below. 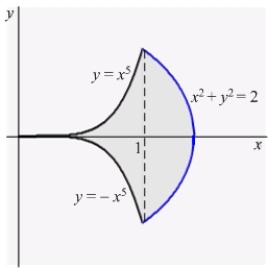


Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
73
In the following figure, the centroid of the region enclosed by the graphs of 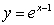 ,
, 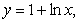 and
and 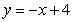 lies on:
lies on: 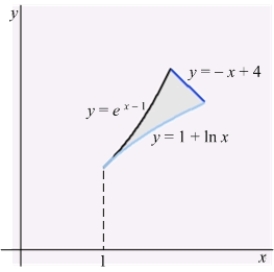
A) the line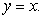
B) the line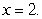
C) the line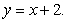
D) the graph of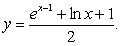
E) the graph of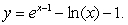
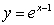 ,
, 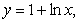 and
and 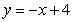 lies on:
lies on: 
A) the line
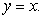
B) the line
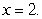
C) the line
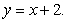
D) the graph of
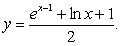
E) the graph of
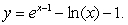

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
74
Find 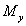 for the lamina of uniform density
for the lamina of uniform density 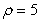 occupying the region under
occupying the region under 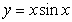 from
from 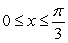 .
.
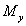 for the lamina of uniform density
for the lamina of uniform density 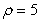 occupying the region under
occupying the region under 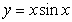 from
from 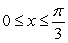 .
.
Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
75
Find the centroid of the shaded region shown in the figure below. 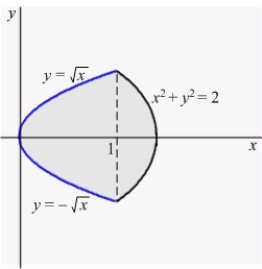


Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
76
Calculate the Maclaurin polynomial 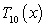 for
for 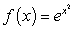 .
.
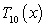 for
for 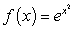 .
.
Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
77
Which of the following are Maclaurin polynomials of 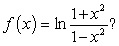
A)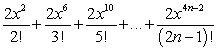
B)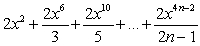
C)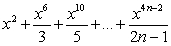
D)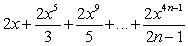
E)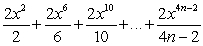
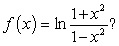
A)
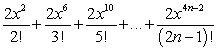
B)
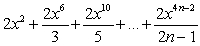
C)
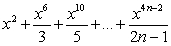
D)
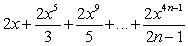
E)
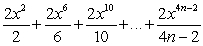

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
78
The centroid of the region shown in the figure below enclosed by the graphs of 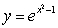 ,
, 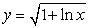 , and
, and 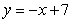 lies on:
lies on: 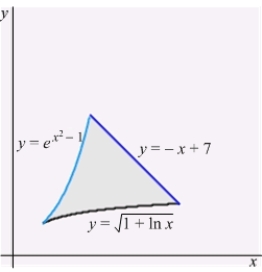
A) the line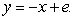
B) the line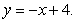
C) the line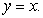
D) the graph of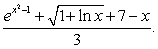
E) the graph of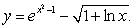
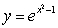 ,
, 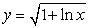 , and
, and 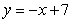 lies on:
lies on: 
A) the line
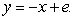
B) the line
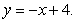
C) the line
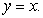
D) the graph of
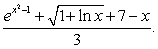
E) the graph of
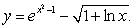

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
79
Four particles with masses of 4, 5, 7, and 3 are located respectively at 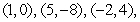 and
and 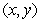 . Find
. Find 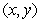 such that the center of mass of the system is located at the point
such that the center of mass of the system is located at the point 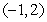 .
.
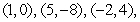 and
and 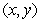 . Find
. Find 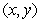 such that the center of mass of the system is located at the point
such that the center of mass of the system is located at the point 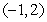 .
.
Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
80
Calculate the Maclaurin polynomial 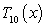 for
for 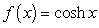 .
.
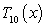 for
for 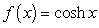 .
.
Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck


