Deck 6: Applications of the Integral
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/80
Play
Full screen (f)
Deck 6: Applications of the Integral
1
Find the area of the shaded region bounded by the graphs of 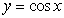 and
and 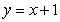 and the
and the 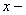 axis.
axis. 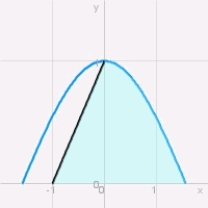
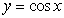 and
and 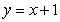 and the
and the 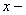 axis.
axis. 
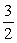
2
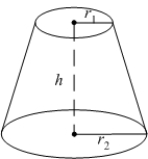
Find the volume of the solid shown in the figure if the radius of the upper circle is 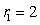 , the radius of the bottom circle is
, the radius of the bottom circle is 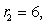 and the height of the solid is
and the height of the solid is 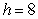 .
. 
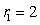 , the radius of the bottom circle is
, the radius of the bottom circle is 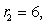 and the height of the solid is
and the height of the solid is 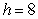 .
. 
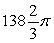
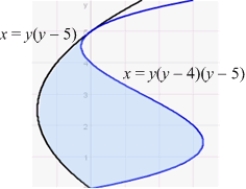
3
Find the area of the region enclosed by the curves 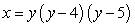 and
and 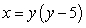 .
. 
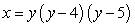 and
and 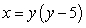 .
. 
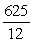
4
The base of a solid is the region bounded by the 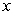 -axis and the semi-ellipse
-axis and the semi-ellipse 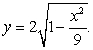 Each cross section perpendicular to the base and parallel to the
Each cross section perpendicular to the base and parallel to the 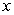 -axis is an isosceles triangle whose height is twice its base. Find the volume of this solid.
-axis is an isosceles triangle whose height is twice its base. Find the volume of this solid. 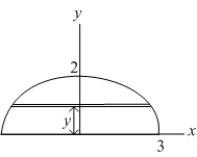

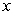 -axis and the semi-ellipse
-axis and the semi-ellipse 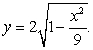 Each cross section perpendicular to the base and parallel to the
Each cross section perpendicular to the base and parallel to the 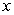 -axis is an isosceles triangle whose height is twice its base. Find the volume of this solid.
-axis is an isosceles triangle whose height is twice its base. Find the volume of this solid. 


Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
5
Find the area of the shaded region below which is bounded by the graphs of 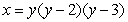 and
and 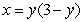 .
. 
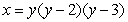 and
and 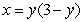 .
. 

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
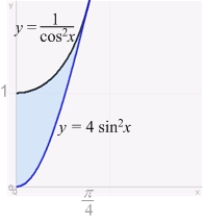
6
Calculate the area of the region enclosed by 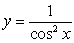 and
and 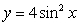 for
for 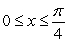 .
. 
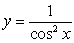 and
and 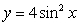 for
for 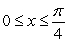 .
. 

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
7
Find the area of the region shown in the figure. Use symmetry to facilitate your computation. 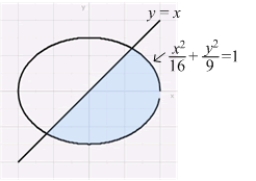


Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
8
Find the area of the region bounded by the graphs of 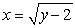 and
and 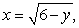 and the y-axis.
and the y-axis. 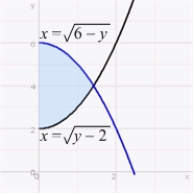
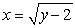 and
and 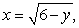 and the y-axis.
and the y-axis. 

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
9
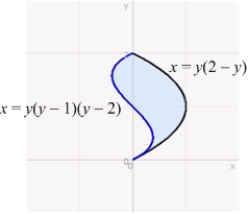
Find the area of the region bounded by 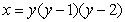 and
and 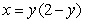 for
for 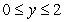 .
. 
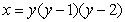 and
and 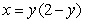 for
for 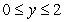 .
. 

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
10
Find the mass of a rod of length 2 with density function 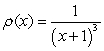 , where
, where 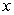 is the distance from one of the rod's ends.
is the distance from one of the rod's ends. 
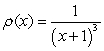 , where
, where 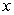 is the distance from one of the rod's ends.
is the distance from one of the rod's ends. 

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
11
Find the mass of a semicircular disc of radius 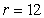 for which the density function is
for which the density function is 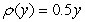 , where
, where 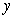 is the distance from the diameter.
is the distance from the diameter. 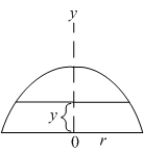
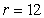 for which the density function is
for which the density function is 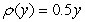 , where
, where 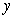 is the distance from the diameter.
is the distance from the diameter. 

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
12
Find the area enclosed by the graphs 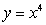 and
and 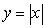 .
.
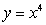 and
and 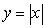 .
.
Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
13
Let 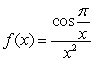 . Find an equation for
. Find an equation for 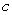 in the interval
in the interval 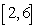 such that
such that 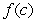 is equal to the average of
is equal to the average of  on
on 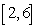 . Use Newton's Method with
. Use Newton's Method with 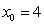 . Give your answer to three decimal places.
. Give your answer to three decimal places.
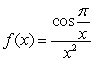 . Find an equation for
. Find an equation for 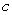 in the interval
in the interval 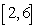 such that
such that 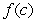 is equal to the average of
is equal to the average of 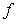 on
on 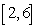 . Use Newton's Method with
. Use Newton's Method with 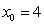 . Give your answer to three decimal places.
. Give your answer to three decimal places.
Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
14
Calculate the total area between the graphs of the functions 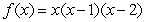 and
and 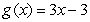 .
.
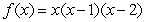 and
and 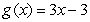 .
.
Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
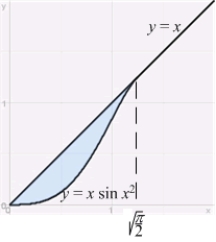
15
Find the area of the region bounded by the graphs of 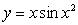 and
and 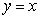 .
. 
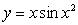 and
and 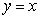 .
. 

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
16
Find the area of the shaded region below which is bounded by the graphs of 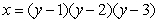 and
and 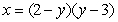 .
. 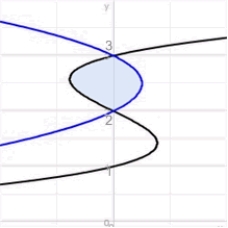
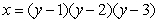 and
and 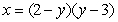 .
. 

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
17
Find the area of the region bounded by the graphs of the functions 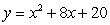 and
and 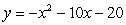 .
.
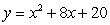 and
and 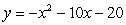 .
.
Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
18
Find the area of the shaded region shown in the figure. 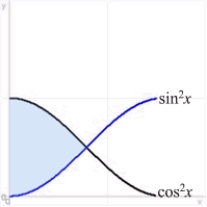


Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
19
Find the volume of the solid whose base is the semi-circular region 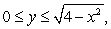 and the cross sections perpendicular to the y-axis are isosceles right triangles whose hypotenuse lie on the base of the solid.
and the cross sections perpendicular to the y-axis are isosceles right triangles whose hypotenuse lie on the base of the solid. 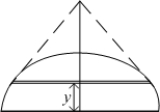
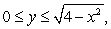 and the cross sections perpendicular to the y-axis are isosceles right triangles whose hypotenuse lie on the base of the solid.
and the cross sections perpendicular to the y-axis are isosceles right triangles whose hypotenuse lie on the base of the solid. 

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
20
Find the area of the region bounded by the graphs of 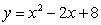 and
and 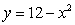 .
.
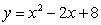 and
and 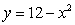 .
.
Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
21
Compute the volume of the solid whose base is the region between the x-axis and the curve 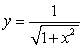 over
over 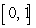 , and the cross sections parallel to the y-axis and perpendicular to the base are semicircles.
, and the cross sections parallel to the y-axis and perpendicular to the base are semicircles. 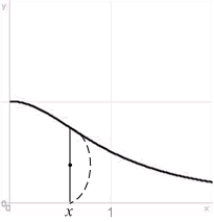
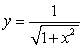 over
over 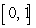 , and the cross sections parallel to the y-axis and perpendicular to the base are semicircles.
, and the cross sections parallel to the y-axis and perpendicular to the base are semicircles. 

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
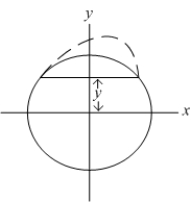
22
Find the mass of the solid whose base is the region inside the unit circle 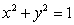 , and the cross sections parallel to the x-axis and perpendicular to the base are semicircles whose diameters are on the base.
, and the cross sections parallel to the x-axis and perpendicular to the base are semicircles whose diameters are on the base.
The density function is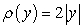 .
. 
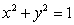 , and the cross sections parallel to the x-axis and perpendicular to the base are semicircles whose diameters are on the base.
, and the cross sections parallel to the x-axis and perpendicular to the base are semicircles whose diameters are on the base.The density function is
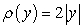 .
. 

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
23
Calculate the population within a 2-mile radius of a city center if the radial population density is 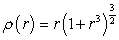 thousands per square mile.
thousands per square mile.
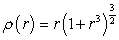 thousands per square mile.
thousands per square mile.
Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
24
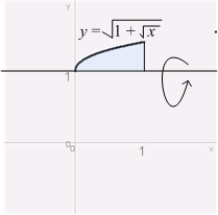
Find the volume of the solid obtained by revolving the region 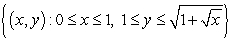 about the line
about the line  .
. 
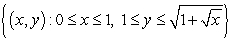 about the line
about the line 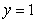 .
. 

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
25
Calculate the population within a 2-mile radius of a city center if the radial population density is 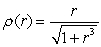 thousands per square mile.
thousands per square mile.
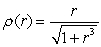 thousands per square mile.
thousands per square mile.
Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
26
A solid circular cylinder of radius 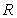 and length
and length 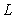 whose density is the square of the distance from the axis of symmetry has the following mass:
whose density is the square of the distance from the axis of symmetry has the following mass:
A)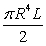 .
.
B)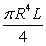 .
.
C)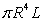 .
.
D)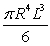 .
.
E)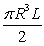 .
.
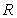 and length
and length 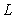 whose density is the square of the distance from the axis of symmetry has the following mass:
whose density is the square of the distance from the axis of symmetry has the following mass:A)
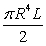 .
.B)
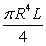 .
.C)
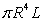 .
.D)
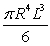 .
.E)
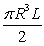 .
.
Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
27
Compute the volume of the solid whose base is the region between the x-axis and the curve 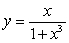 over
over 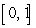 , and the cross sections parallel to the y-axis and perpendicular to the base are squares.
, and the cross sections parallel to the y-axis and perpendicular to the base are squares. 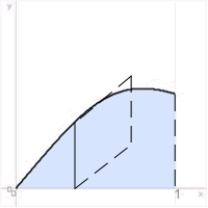
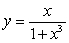 over
over 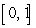 , and the cross sections parallel to the y-axis and perpendicular to the base are squares.
, and the cross sections parallel to the y-axis and perpendicular to the base are squares. 

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
28
The volume of the solid obtained by rotating the ellipse 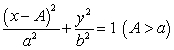 about the y-axis is
about the y-axis is 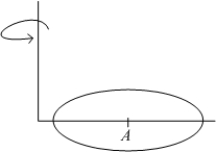
A)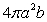
B)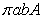
C)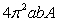
D)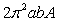
E) none of the above.
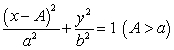 about the y-axis is
about the y-axis is 
A)
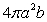
B)
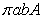
C)
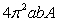
D)
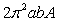
E) none of the above.

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
29
Find the value of 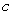 in
in 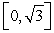 such that
such that 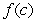 is equal to the average of
is equal to the average of  on
on 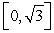 where
where 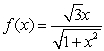 .
.
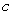 in
in 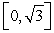 such that
such that 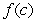 is equal to the average of
is equal to the average of 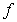 on
on 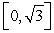 where
where 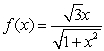 .
.
Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
30
Find the mass of a rod of length 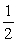 aligned on the positive
aligned on the positive 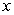 -axis if its mass density
-axis if its mass density 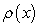 equals the area of the right triangle shown in the figure.
equals the area of the right triangle shown in the figure. 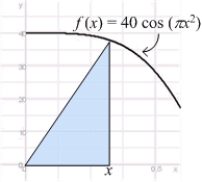
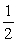 aligned on the positive
aligned on the positive 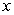 -axis if its mass density
-axis if its mass density 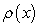 equals the area of the right triangle shown in the figure.
equals the area of the right triangle shown in the figure. 

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
31
Find a value 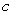 in
in 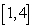 such that
such that 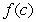 is equal to the average of
is equal to the average of 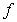 on
on 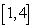 if
if 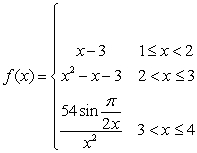
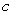 in
in 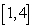 such that
such that 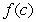 is equal to the average of
is equal to the average of 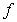 on
on 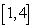 if
if 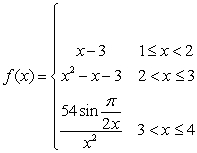

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
32
Find the volume of the solid obtained by revolving the region 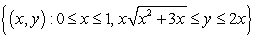 about the x-axis.
about the x-axis. 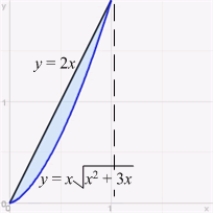
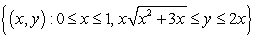 about the x-axis.
about the x-axis. 

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
33
Find the volume of the solid obtained by rotating the region 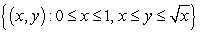 about the line
about the line 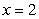 .
. 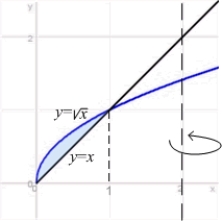
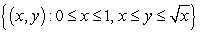 about the line
about the line 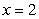 .
. 

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
34
Find the volume generated by revolving the triangle shown in the figure about side 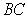 .
. 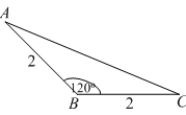
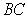 .
. 

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
35
Find the volume generated by revolving a right triangle with angle 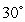 and hypotenuse 2 about a line perpendicular to the hypotenuse passing through the vertex of the
and hypotenuse 2 about a line perpendicular to the hypotenuse passing through the vertex of the 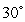 angle, as shown in the figure.
angle, as shown in the figure. 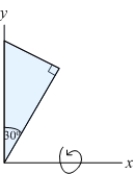

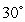 and hypotenuse 2 about a line perpendicular to the hypotenuse passing through the vertex of the
and hypotenuse 2 about a line perpendicular to the hypotenuse passing through the vertex of the 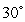 angle, as shown in the figure.
angle, as shown in the figure. 


Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
36
The volume of the ice goblet obtained by rotating the region shown in the figure about the y-axis is 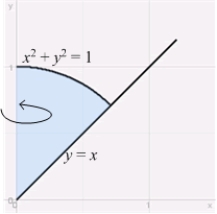
A)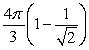 .
.
B)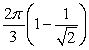 .
.
C)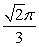 .
.
D)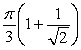 .
.
E)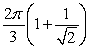 .
.

A)
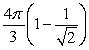 .
.B)
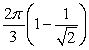 .
.C)
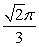 .
.D)
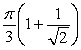 .
.E)
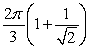 .
.
Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
37
Calculate the population within a 4-mile radius of a city center if the radial population density is 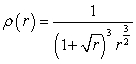 thousands per square mile.
thousands per square mile.
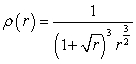 thousands per square mile.
thousands per square mile.
Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
38
What is the average volume of a regular tetrahedron with side 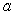 if
if 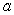 varies from 1 to 4?
varies from 1 to 4? 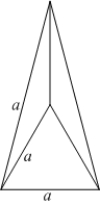
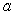 if
if 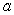 varies from 1 to 4?
varies from 1 to 4? 

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
39
Find the volume of the solid obtained by revolving the region in the first quadrant between the curves 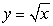 and
and 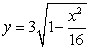 about the line
about the line 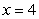 .
. 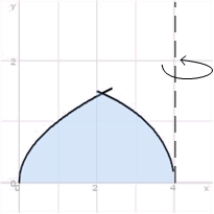
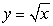 and
and 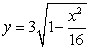 about the line
about the line 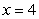 .
. 

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
40
Find the value of 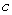 in
in 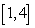 such that
such that 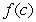 is equal to the average of
is equal to the average of 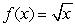 on
on 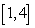 .
.
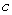 in
in 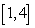 such that
such that 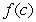 is equal to the average of
is equal to the average of 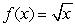 on
on 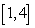 .
.
Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
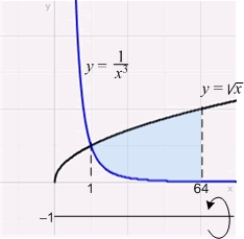
41
Find the volume of the solid obtained by rotating the region shown in the figure about the line 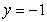 .
. 
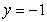 .
. 

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
42
The volume of the solid obtained by rotating the region shown in the figure about the y-axis is 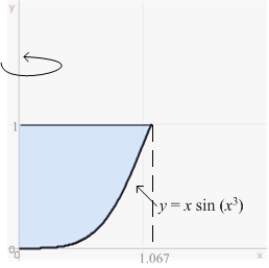
A)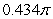 .
.
B)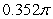 .
.
C)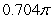 .
.
D)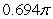 .
.
E) none of the above.

A)
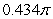 .
.B)
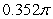 .
.C)
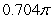 .
.D)
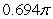 .
.E) none of the above.

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
43
Find the volume of the solid obtained by rotating the region 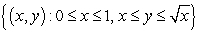 about the line
about the line 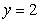 .
. 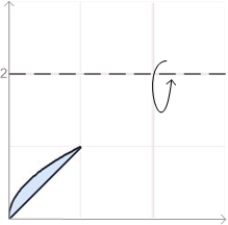
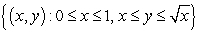 about the line
about the line 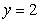 .
. 

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
44
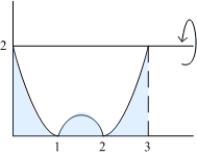
Find the volume of the solid obtained by rotating the region between the curve 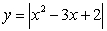 and the x-axis above the interval
and the x-axis above the interval 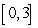 about the line
about the line 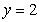 .
. 
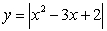 and the x-axis above the interval
and the x-axis above the interval 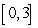 about the line
about the line 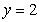 .
. 

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
45
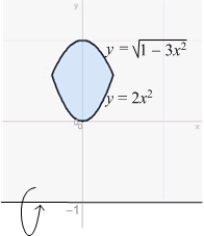
Find the volume of the solid obtained by rotating the region between the curves 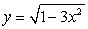 and
and 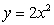 about the line
about the line 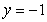 . Use the formula
. Use the formula 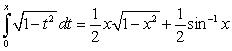 .
. 
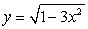 and
and 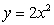 about the line
about the line 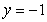 . Use the formula
. Use the formula 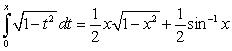 .
. 

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
46
Find the volume of the solid obtained by rotating the region in the first quadrant enclosed by the curves 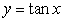 and
and 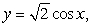 for
for 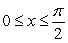 , about the line
, about the line 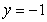 .
. 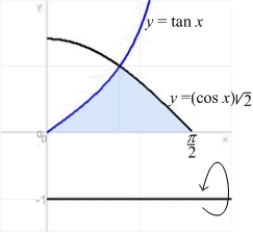
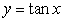 and
and 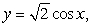 for
for 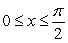 , about the line
, about the line 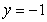 .
. 

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
47
Use the Shell Method to find the volume of the solid obtained by rotating the region shown in the figure about the y-axis. 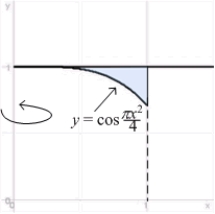


Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
48
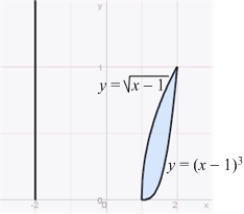
Use the Shell Method to calculate the volume of the solid obtained by rotating the region shown in the figure about the line 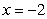 .
. 
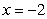 .
. 

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
49
Find the volume generated by revolving an isosceles right triangle with hypotenuse 2 about a line perpendicular to the hypotenuse passing through the vertex of one of the acute angles. 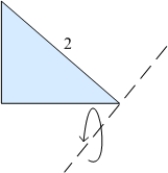


Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
50
The volume of the solid obtained by revolving the region between the lines 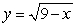 and
and 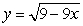 about the y-axis is
about the y-axis is 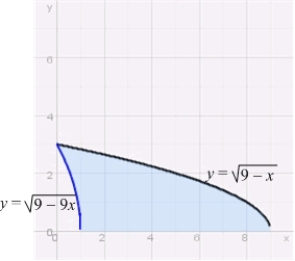
A)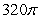 .
.
B)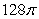 .
.
C)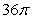 .
.
D)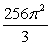 .
.
E)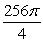 .
.
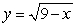 and
and 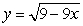 about the y-axis is
about the y-axis is 
A)
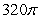 .
.B)
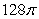 .
.C)
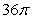 .
.D)
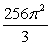 .
.E)
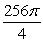 .
.
Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
51
Find the volume of the solid generated by revolving the region below 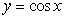 over
over 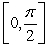 about the line
about the line 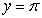 .
. 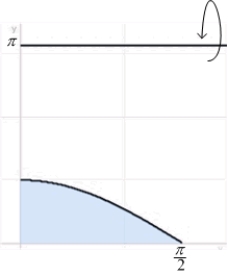
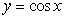 over
over 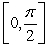 about the line
about the line 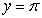 .
. 

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
52
Use the Shell Method to calculate the volume of the solid obtained by rotating the region shown in the figure about the line 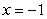 .
. 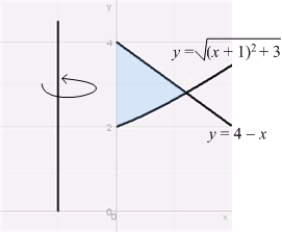
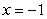 .
. 

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
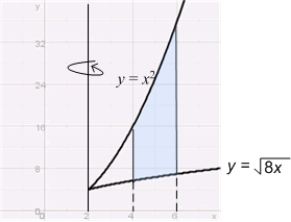
53
Use the Shell Method to calculate the volume of the solid obtained by rotating the region 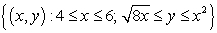 about the line
about the line 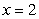 .
. 
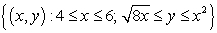 about the line
about the line 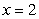 .
. 

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
54
To compute the volume of the solid obtained by rotating the region shown in the figure about the y-axis, the most convenient method is 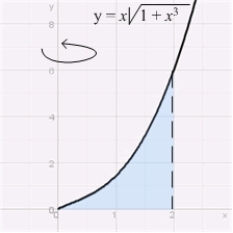
A) the Disk Method.
B) the Disk Method in addition to the Shell Method.
C) the Shell Method.
D) Integration by Parts.
E) none of these methods.

A) the Disk Method.
B) the Disk Method in addition to the Shell Method.
C) the Shell Method.
D) Integration by Parts.
E) none of these methods.

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
55
Find the volume generated by revolving the triangle shown in the figure about a line parallel to the hypotenuse, passing through the vertex of the right angle. 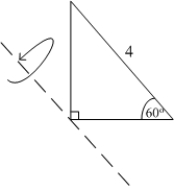


Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
56
To compute the volume of the solid obtained by rotating the region between the line 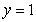 and the curve
and the curve 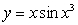 in the first quadrant about the y-axis, the most convenient method is
in the first quadrant about the y-axis, the most convenient method is 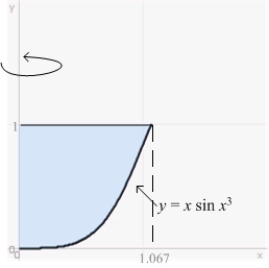
A) the Shell Method.
B) the Disk Method.
C) the Shell Method in addition to the Disk Method.
D) Integration by Parts.
E) none of these methods.
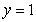 and the curve
and the curve 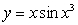 in the first quadrant about the y-axis, the most convenient method is
in the first quadrant about the y-axis, the most convenient method is 
A) the Shell Method.
B) the Disk Method.
C) the Shell Method in addition to the Disk Method.
D) Integration by Parts.
E) none of these methods.

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
57
Calculate the volume of the solid obtained by rotating the region between the curves 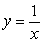 and
and 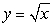 over
over 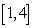 about the line
about the line 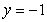 .
. 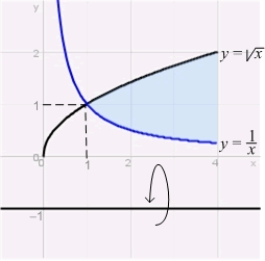
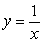 and
and 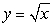 over
over 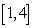 about the line
about the line 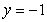 .
. 

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
58
Use the Shell Method to calculate the volume of the solid obtained by rotating the region shown in the figure about the y-axis. 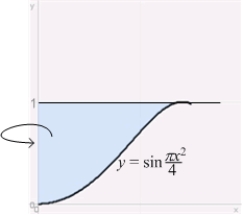




Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
59
Use the Shell Method to calculate the volume of the solid obtained by rotating the region shown in the figure about the y-axis. 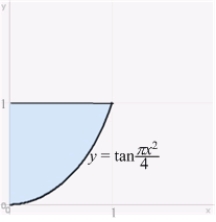


Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
60
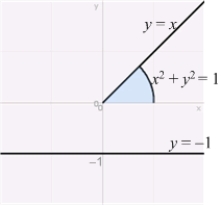
Use the Shell Method to calculate the volume of the solid obtained by rotating the sector shown in the figure about the line 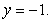 Use the formula
Use the formula 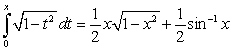 .
. 
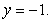 Use the formula
Use the formula 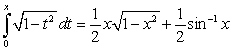 .
. 

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
61
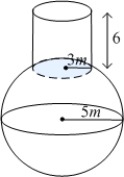
Find the approximate work required to pump water out of the container shown in the figure if the container is filled with water to the top of the cylinder. The density of water is 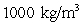 .
. 
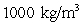 .
. 

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
62
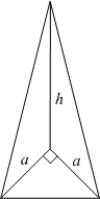
Find the work required to build a pyramid of height 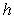 , whose base is an isosceles right triangle with a leg length of
, whose base is an isosceles right triangle with a leg length of 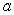 . The pyramid will be built with stones of density
. The pyramid will be built with stones of density 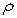 .
. 
A)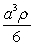
B)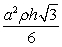
C)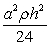
D)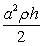
E)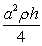
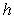 , whose base is an isosceles right triangle with a leg length of
, whose base is an isosceles right triangle with a leg length of 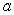 . The pyramid will be built with stones of density
. The pyramid will be built with stones of density 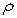 .
. 
A)
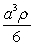
B)
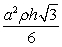
C)
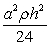
D)
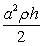
E)
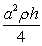

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
63
To compute the volume of the solid obtained by rotating the region in the figure about the y-axis, the most convenient method is 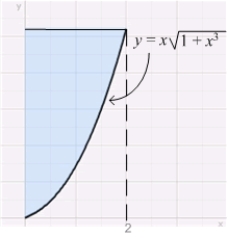
A) the Disk Method.
B) the Shell Method.
C) both the Disk and Shell Methods.
D) Integration by Parts.
E) none of these methods.

A) the Disk Method.
B) the Shell Method.
C) both the Disk and Shell Methods.
D) Integration by Parts.
E) none of these methods.

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
64
Find the work required to move an object along the x-axis from 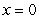 to
to 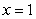 by the force
by the force 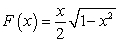 .
.
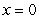 to
to 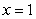 by the force
by the force 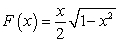 .
.
Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
65
A conical container (vertex down) is filled to half of its height with liquid of density 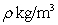 . The radius of the conical container is
. The radius of the conical container is 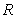 and its height is
and its height is 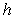 , measured in meters.
, measured in meters.
The approximate work required to pump the liquid out of the top of the tank is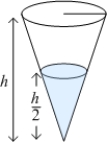
A)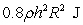
B)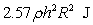
C)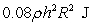
D)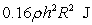
E) none of the above.
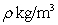 . The radius of the conical container is
. The radius of the conical container is 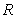 and its height is
and its height is 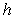 , measured in meters.
, measured in meters.The approximate work required to pump the liquid out of the top of the tank is

A)
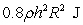
B)
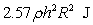
C)
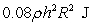
D)
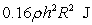
E) none of the above.

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
66
The vertical tank shown in the figure is half full of water. Given that the density of water is 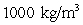 , the approximate work required to empty the tank by pumping the water out through an outlet at the top of the tank is
, the approximate work required to empty the tank by pumping the water out through an outlet at the top of the tank is 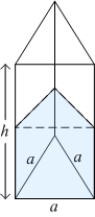
A)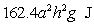
B)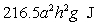
C)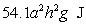
D)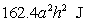
E) none of the above.
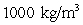 , the approximate work required to empty the tank by pumping the water out through an outlet at the top of the tank is
, the approximate work required to empty the tank by pumping the water out through an outlet at the top of the tank is 
A)
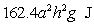
B)
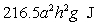
C)
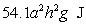
D)
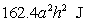
E) none of the above.

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
67
A vertical tank, with elliptic horizontal cross section 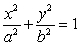 and height
and height 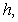 is full of water. The work done in pumping the water out through an outlet at the top of the tank is which of the following? (Assume that the water weighs 62.5 pounds per cubic foot.)
is full of water. The work done in pumping the water out through an outlet at the top of the tank is which of the following? (Assume that the water weighs 62.5 pounds per cubic foot.) 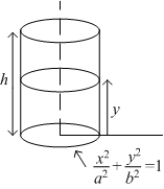
A)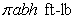
B)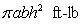
C)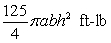
D)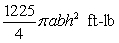
E) None of the above.
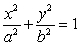 and height
and height 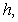 is full of water. The work done in pumping the water out through an outlet at the top of the tank is which of the following? (Assume that the water weighs 62.5 pounds per cubic foot.)
is full of water. The work done in pumping the water out through an outlet at the top of the tank is which of the following? (Assume that the water weighs 62.5 pounds per cubic foot.) 
A)
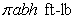
B)
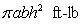
C)
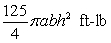
D)
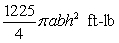
E) None of the above.

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
68
Calculate the volume of the solid obtained by rotating the region shown in the figure about the line 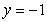 .
. 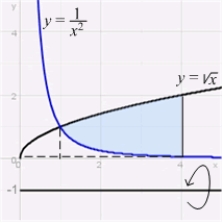
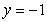 .
. 

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
69
Find the work done in moving an object from 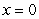 to
to 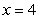 by the force
by the force 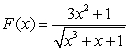 .
.
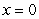 to
to 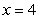 by the force
by the force 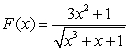 .
.
Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
70
The volume of the solid obtained by rotating the region shown in the figure about the
Y-axis is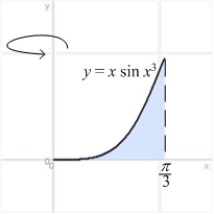
A)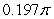 .
.
B)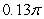 .
.
C)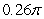 .
.
D)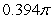 .
.
E)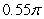 .
.
Y-axis is

A)
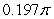 .
.B)
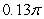 .
.C)
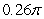 .
.D)
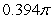 .
.E)
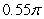 .
.
Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
71
Use the Shell Method to calculate the volume of the solid obtained by rotating the region shown in the figure about the line 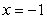 .
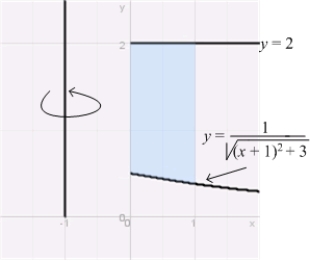
. 
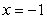 .
. 

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
72
The work (against gravity) required to build a right pyramid of height 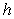 , with equilateral triangle base of side length
, with equilateral triangle base of side length 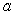 , using stones of density
, using stones of density 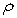 is
is 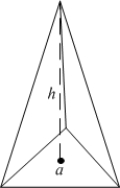
A)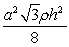 .
.
B)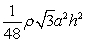 .
.
C)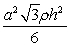 .
.
D)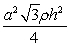 .
.
E) none of the above.
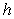 , with equilateral triangle base of side length
, with equilateral triangle base of side length 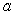 , using stones of density
, using stones of density 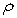 is
is 
A)
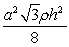 .
.B)
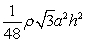 .
.C)
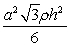 .
.D)
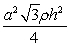 .
.E) none of the above.

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
73
If 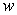 Joules of work are needed to stretch a spring
Joules of work are needed to stretch a spring 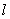 cm beyond equilibrium, the spring constant
cm beyond equilibrium, the spring constant 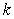 is
is
A)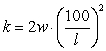 .
.
B)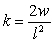 .
.
C)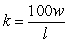 .
.
D)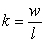 .
.
E)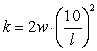 .
.
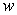 Joules of work are needed to stretch a spring
Joules of work are needed to stretch a spring 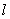 cm beyond equilibrium, the spring constant
cm beyond equilibrium, the spring constant 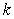 is
isA)
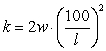 .
.B)
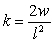 .
.C)
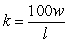 .
.D)
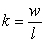 .
.E)
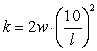 .
.
Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
74
A vertical cylindrical tank of radius 5 feet and height 12 feet is full of water. The water weighs 62.5 pounds per cubic foot. Find the work done in pumping out the water:
A) through an outlet at the top of the tank.
B) through an outlet 6 feet above the top of the tank.
A) through an outlet at the top of the tank.
B) through an outlet 6 feet above the top of the tank.

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
75
A chain weighing 25 pounds per foot is hanging from the top of a 100-foot building, as shown in the figure. Find the work needed to pull the chain to the top of the building. 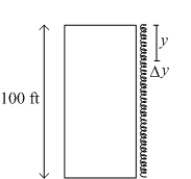


Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
76
Calculate the volume of the solid obtained by rotating the region in the figure about the y-axis. (Note: the x and y scales are different.) 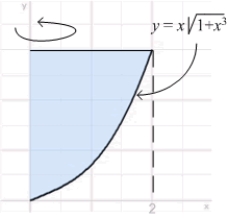


Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
77
Find the work done in moving an object from 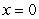 to
to 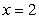 by the force
by the force 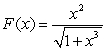 .
.
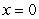 to
to 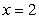 by the force
by the force 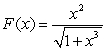 .
.
Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
78
Find the work done in moving an object from 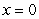 to
to 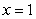 by the force
by the force 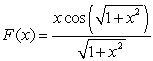 .
.
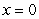 to
to 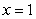 by the force
by the force 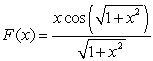 .
.
Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
79
To compute the volume of the solid obtained by rotating the region shown in the figure about the y-axis, the most convenient method is 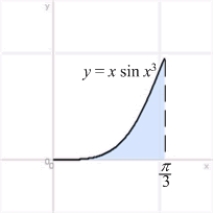
A) the Disk Method.
B) the Shell Method.
C) the Disk and Shell Methods.
D) Integration by Parts.
E) none of these methods.

A) the Disk Method.
B) the Shell Method.
C) the Disk and Shell Methods.
D) Integration by Parts.
E) none of these methods.

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
80
Use the Shell Method to find the volume of the solid obtained by rotating the region shown in the figure about the line 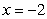 .
. 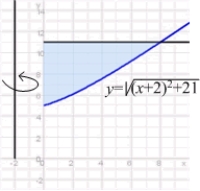
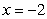 .
. 

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck


