Deck 5: The Integral
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/82
Play
Full screen (f)
Deck 5: The Integral
1
Calculate the following sums:
A)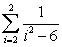
B)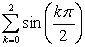
C)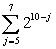
A)
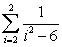
B)
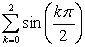
C)
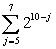
A) 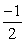 B)
B) 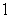 C) 56
C) 56
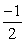 B)
B) 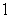 C) 56
C) 56 2
Use a definite integral to evaluate 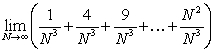
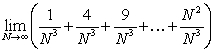
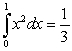
3
Let 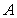 be the area under the graph of
be the area under the graph of 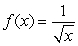 over
over 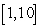 . Use
. Use 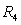 and
and 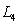 to find constants
to find constants 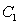 and
and 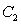 so that
so that 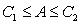
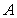 be the area under the graph of
be the area under the graph of 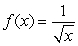 over
over 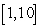 . Use
. Use 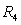 and
and 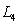 to find constants
to find constants 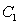 and
and 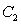 so that
so that 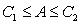
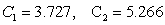

4
Use the global extrema of 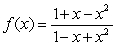 on
on 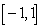 to find constants
to find constants 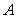 and
and 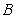 such that
such that 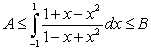 .
.
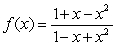 on
on 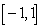 to find constants
to find constants 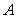 and
and 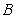 such that
such that 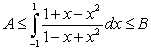 .
.
Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
5
Calculate 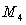 for the function
for the function 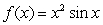 over
over 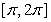 .
.
 for the function
for the function 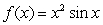 over
over 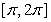 .
.
Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
6
Assume that 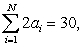
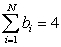 , and
, and 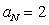 . Calculate the following:
. Calculate the following:
A)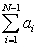
B)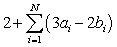
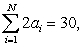
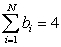 , and
, and 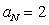 . Calculate the following:
. Calculate the following: A)
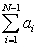
B)
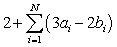

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
7
Calculate 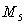 to five decimal places for
to five decimal places for 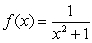 over
over 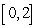 .
.
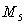 to five decimal places for
to five decimal places for 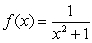 over
over 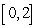 .
.
Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
8
Let 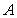 be the area under
be the area under 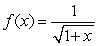 over
over 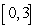 .
.
Which of the following is correct?
A)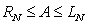 , hence
, hence 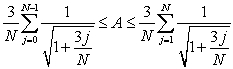 .
.
B)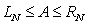 , hence
, hence 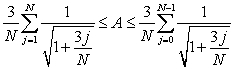 .
.
C)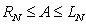 , hence
, hence 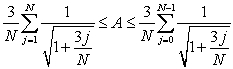 .
.
D)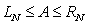 , hence
, hence 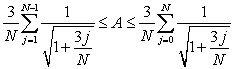 .
.
E) None of the above.
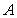 be the area under
be the area under 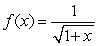 over
over 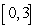 .
.Which of the following is correct?
A)
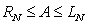 , hence
, hence 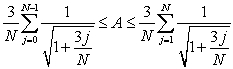 .
.B)
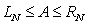 , hence
, hence 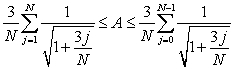 .
.C)
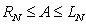 , hence
, hence 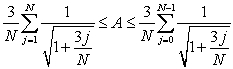 .
.D)
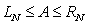 , hence
, hence 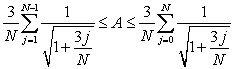 .
.E) None of the above.

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
9
Compute 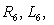 and
and 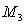 over
over 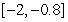 using the following values.
using the following values. 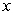
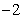
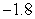
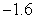
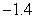
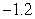
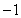
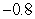
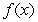 1.2
1.2
.75
.4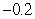
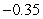
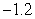 2.5
2.5
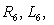 and
and 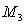 over
over 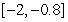 using the following values.
using the following values. 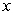
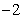
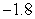
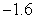
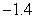
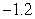
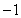
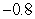
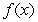 1.2
1.2.75
.4
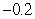
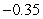
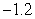 2.5
2.5
Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
10
Let 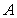 be the area of the trapezoid shown in the figure.
be the area of the trapezoid shown in the figure.
A) Evaluate the right-endpoint approximation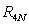 .
.
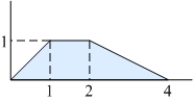
B) Compute the area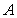 using geometry and verify
using geometry and verify 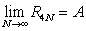 .
. 
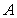 be the area of the trapezoid shown in the figure.
be the area of the trapezoid shown in the figure. A) Evaluate the right-endpoint approximation
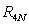 .
. B) Compute the area
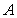 using geometry and verify
using geometry and verify 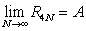 .
. 

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
11
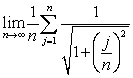 is equal to which of the following definite integrals?
is equal to which of the following definite integrals?A)
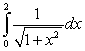
B)
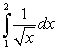
C)
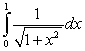
D)
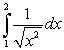
E)
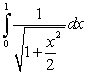

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
12
Calculate 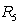 for the function
for the function 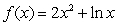 over
over 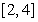 .
.
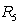 for the function
for the function 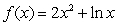 over
over 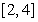 .
.
Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
13
Find the area under the graph of 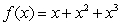 over the interval
over the interval 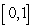 by computing
by computing 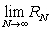 . The area is
. The area is
A)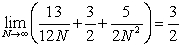
B)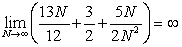
C)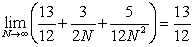
D)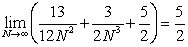
E)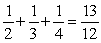
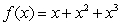 over the interval
over the interval 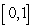 by computing
by computing 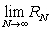 . The area is
. The area isA)
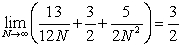
B)
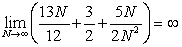
C)
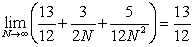
D)
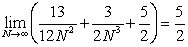
E)
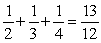

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
14
Compute the area under the graph of 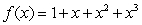 over
over 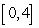 as the limit of
as the limit of 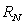 as
as 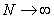 .
.
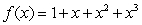 over
over 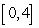 as the limit of
as the limit of 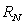 as
as 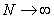 .
.
Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
15
Evaluate the integral 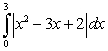 .
.
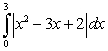 .
.
Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
16
Let 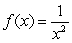 . Calculate
. Calculate 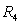 ,
, 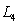 , and
, and 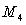 for the interval
for the interval 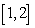 . Give your answer to four decimal places.
. Give your answer to four decimal places.
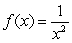 . Calculate
. Calculate 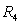 ,
, 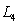 , and
, and 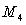 for the interval
for the interval 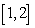 . Give your answer to four decimal places.
. Give your answer to four decimal places.
Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
17
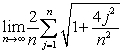 is equal to which of the following integrals?
is equal to which of the following integrals?A)
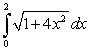
B)
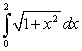
C)
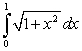
D)
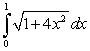
E)
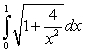

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
18
Using the global extrema of 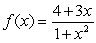 on
on 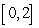 , find
, find 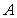 and
and 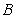 such that
such that 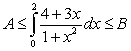
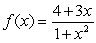 on
on 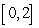 , find
, find 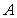 and
and 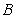 such that
such that 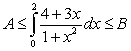

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
19
Bernoulli's Formula 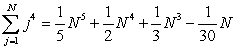 and the limit of the right-endpoint approximation lead to which the following integrals?
and the limit of the right-endpoint approximation lead to which the following integrals?
A)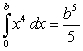
B)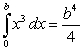
C)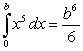
D)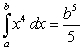
E) Bernoulli's Formula is not related to any of these integrals.
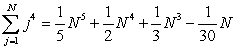 and the limit of the right-endpoint approximation lead to which the following integrals?
and the limit of the right-endpoint approximation lead to which the following integrals?A)
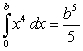
B)
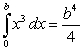
C)
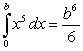
D)
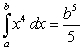
E) Bernoulli's Formula is not related to any of these integrals.

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
20
Match the approximation with the corresponding function 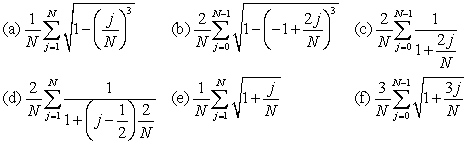
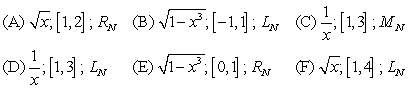
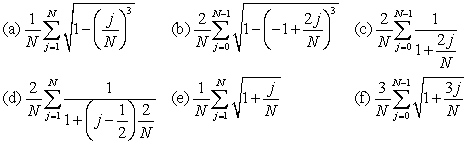
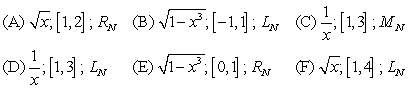

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
21
The graph of 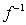 is obtained by reflecting the graph of
is obtained by reflecting the graph of 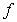 through
through 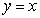 .
. 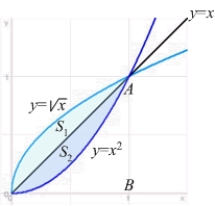 Let
Let 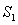 and
and 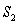 denote the area in the figure. The following equality holds:
denote the area in the figure. The following equality holds:
A)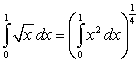
B)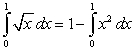
C)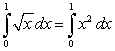
D)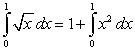
 is obtained by reflecting the graph of
is obtained by reflecting the graph of  through
through 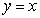 .
.  Let
Let 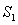 and
and 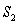 denote the area in the figure. The following equality holds:
denote the area in the figure. The following equality holds:A)
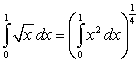
B)
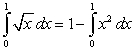
C)
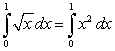
D)
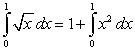

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
22
Use a trigonometric identity to evaluate the integral 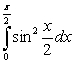 .
.
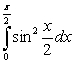 .
.
Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
23
Evaluate the following integrals using the Fundamental Theorem of Calculus, Part I:
A)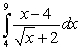
B)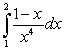
C)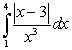
A)
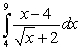
B)
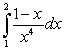
C)
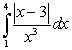

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
24
Let 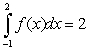 ,
, 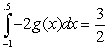 ,
, 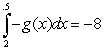 and
and 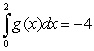 Calculate the following
Calculate the following
(A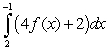 (B
(B 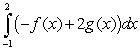 (C
(C 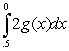
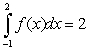 ,
, 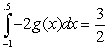 ,
, 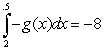 and
and 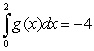 Calculate the following
Calculate the following(A
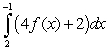 (B
(B 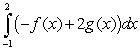 (C
(C 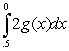

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
25
Let 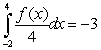 ,
, 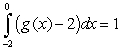 ,
, 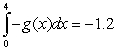 and
and 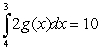 Calculate
Calculate
(A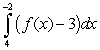 (B
(B 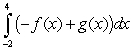 (C
(C 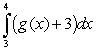
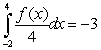 ,
, 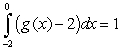 ,
, 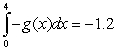 and
and 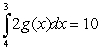 Calculate
Calculate(A
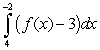 (B
(B 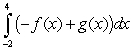 (C
(C 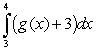

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
26
Use the global extrema of 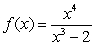 on
on 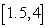 to find constants
to find constants 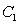 and
and 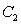 such that
such that 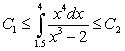 .
.
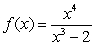 on
on 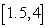 to find constants
to find constants 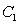 and
and 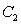 such that
such that 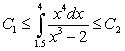 .
.
Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
27
Use trigonometric identities to evaluate the integral 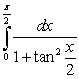 .
.
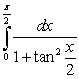 .
.
Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
28
Solve the initial value problem 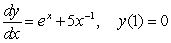 .
.
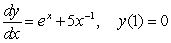 .
.
Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
29
The area between the 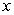 -axis and the graph of
-axis and the graph of 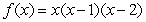 on
on 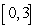 is.
is.
A)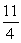
B)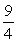
C)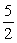
D)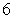
E)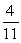
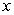 -axis and the graph of
-axis and the graph of 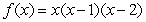 on
on 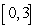 is.
is.A)
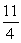
B)
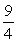
C)
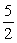
D)
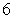
E)
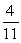

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
30
Evaluate the following integrals using the Fundamental Theorem of Calculus, Part I:
A)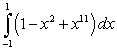
B)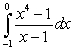
C)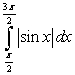
A)
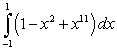
B)
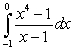
C)
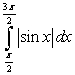

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
31
Find the general antiderivative of 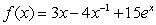 .
.
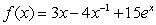 .
.
Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
32
Evaluate the following integrals using the Fundamental Theorem of Calculus, Part I:
A)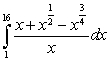
B)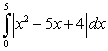
C)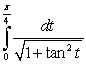
A)
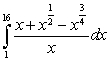
B)
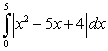
C)
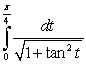

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
33
Evaluate 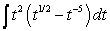 .
.
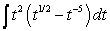 .
.
Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
34
The area between the 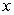 -axis and the graph of
-axis and the graph of 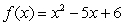 on
on 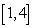 is
is
A)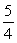
B)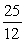
C)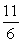
D)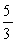
E)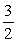
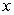 -axis and the graph of
-axis and the graph of 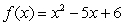 on
on 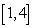 is
isA)
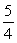
B)
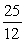
C)
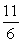
D)
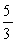
E)
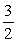

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
35
Evaluate the integral 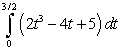 .
.
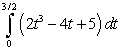 .
.
Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
36
Solve the initial value problem 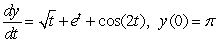 .
.
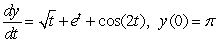 .
.
Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
37
Evaluate the integral 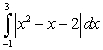 .
.
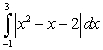 .
.
Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
38
Evaluate 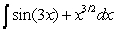 .
.
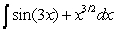 .
.
Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
39
Let 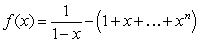 for some nonnegative integer
for some nonnegative integer 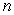 . Which of the following statements is correct? (Hint:
. Which of the following statements is correct? (Hint: 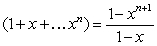 )
)
A) is increasing on
is increasing on  , hence
, hence 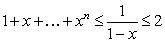 .
.
B)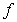 is increasing on
is increasing on 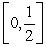 and
and 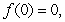 hence
hence 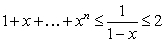 .
.
C)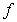 is decreasing on
is decreasing on 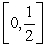 and
and 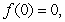 hence
hence 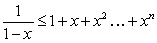 .
.
D)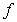 is decreasing on
is decreasing on 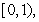 hence
hence 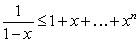 .
.
E) None of the above.
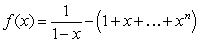 for some nonnegative integer
for some nonnegative integer 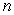 . Which of the following statements is correct? (Hint:
. Which of the following statements is correct? (Hint: 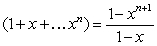 )
)A)
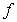 is increasing on
is increasing on 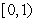 , hence
, hence 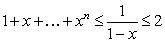 .
.B)
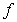 is increasing on
is increasing on 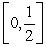 and
and 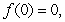 hence
hence 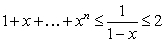 .
.C)
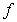 is decreasing on
is decreasing on  and
and  hence
hence 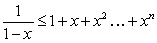 .
.D)
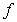 is decreasing on
is decreasing on  hence
hence 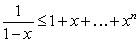 .
.E) None of the above.

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
40
The Mean Value Theorem and the Comparison Theorem imply that
A)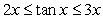 for
for 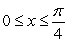 and
and 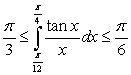 .
.
B)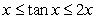 for
for 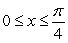 and
and 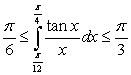 .
.
C)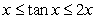 for
for 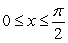 and
and 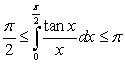 .
.
D)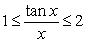 for
for 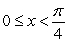 and
and 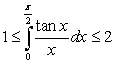 .
.
E) None of the above.
A)
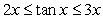 for
for 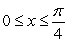 and
and 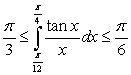 .
.B)
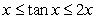 for
for 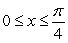 and
and 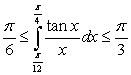 .
.C)
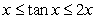 for
for 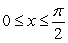 and
and 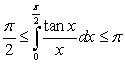 .
.D)
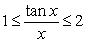 for
for 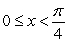 and
and 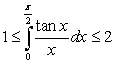 .
.E) None of the above.

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
41
A population is increasing at a rate of 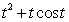 individuals per year.
individuals per year.
Use the Fundamental Theorem of Calculus Part II to verify that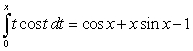 , then find the population after 9 years given that at
, then find the population after 9 years given that at 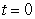 the population was 16 individuals. Give your answer to one decimal place.
the population was 16 individuals. Give your answer to one decimal place.
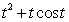 individuals per year.
individuals per year.Use the Fundamental Theorem of Calculus Part II to verify that
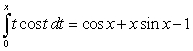 , then find the population after 9 years given that at
, then find the population after 9 years given that at 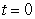 the population was 16 individuals. Give your answer to one decimal place.
the population was 16 individuals. Give your answer to one decimal place.
Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
42
Calculate 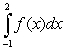 , where
, where 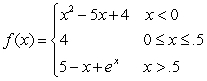 .
.
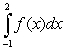 , where
, where 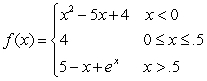 .
.
Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
43
Calculate 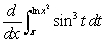 .
.
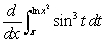 .
.
Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
44
The graph of 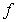 on
on 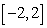 is shown in the following figure:
is shown in the following figure: 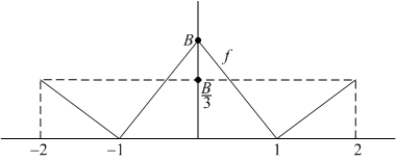
A) Explain why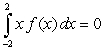 without evaluating the integral.
without evaluating the integral.
B) Find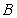 if
if 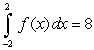 .
.
C) Consider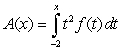 . What is the value of
. What is the value of 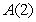 ?
?
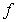 on
on 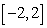 is shown in the following figure:
is shown in the following figure: 
A) Explain why
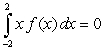 without evaluating the integral.
without evaluating the integral. B) Find
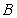 if
if 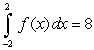 .
. C) Consider
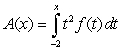 . What is the value of
. What is the value of 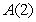 ?
?
Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
45
Evaluate the following limits using L'Hopital's Rule and the Fundamental Theorem of Calculus, Part II:
A)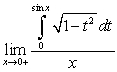
B)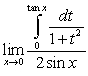
C)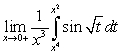
A)
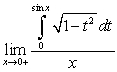
B)
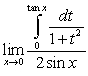
C)
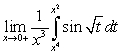

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
46
Consider the following functions. 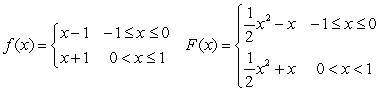 The following statement is correct:
The following statement is correct:
A)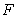 is an antiderivative of
is an antiderivative of 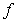 on
on 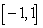 by the Fundamental Theorem of Calculus, Part II.
by the Fundamental Theorem of Calculus, Part II.
B) is not an antiderivative of
is not an antiderivative of  on
on 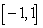 since
since 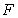 is not differentiable at
is not differentiable at 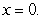
C)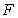 is not an antiderivative of
is not an antiderivative of 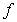 on
on 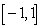 since
since  is not the area function of
is not the area function of 
D) If we change the definition of at
at 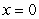 such that
such that 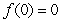 , then
, then 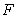 is an antiderivative of
is an antiderivative of 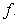
E)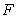 is not an antiderivative of
is not an antiderivative of 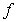 on
on 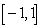 since
since 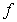 is not differentiable at
is not differentiable at 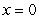 .
.
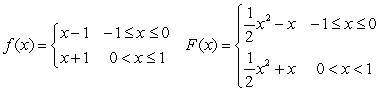 The following statement is correct:
The following statement is correct:A)
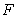 is an antiderivative of
is an antiderivative of 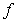 on
on 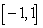 by the Fundamental Theorem of Calculus, Part II.
by the Fundamental Theorem of Calculus, Part II.B)
 is not an antiderivative of
is not an antiderivative of  on
on 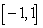 since
since 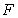 is not differentiable at
is not differentiable at 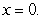
C)
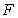 is not an antiderivative of
is not an antiderivative of 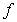 on
on 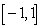 since
since 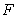 is not the area function of
is not the area function of 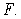
D) If we change the definition of
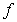 at
at 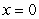 such that
such that 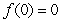 , then
, then 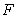 is an antiderivative of
is an antiderivative of 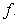
E)
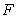 is not an antiderivative of
is not an antiderivative of 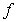 on
on 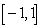 since
since 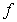 is not differentiable at
is not differentiable at 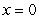 .
.
Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
47
Let 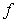 be the function shown in the figure:
be the function shown in the figure: 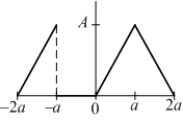
 Given that:
Given that: 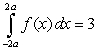 and
and 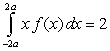
A) Find the constants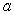 and
and 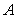 .
.
B) Determine the cumulative area function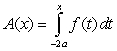 , and give the value
, and give the value 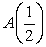 .
.
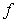 be the function shown in the figure:
be the function shown in the figure: 
 Given that:
Given that: 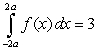 and
and 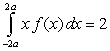
A) Find the constants
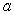 and
and 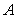 .
. B) Determine the cumulative area function
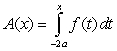 , and give the value
, and give the value 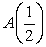 .
.
Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
48
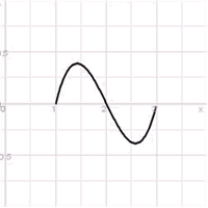
The velocity of a particle is 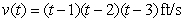 .
.
A) Find the displacement over the intervals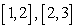 , and
, and 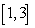 .
.
B) Find the total distance traveled over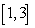 .
. 
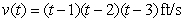 .
. A) Find the displacement over the intervals
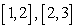 , and
, and 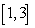 .
. B) Find the total distance traveled over
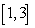 .
. 

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
49
Evaluate the following limits using L'Hopital's Rule and the Fundamental Theorem of Calculus, Part II:
A)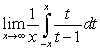
B)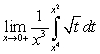
A)
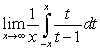
B)
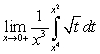

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
50
A population is increasing at a rate of 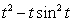 individuals per year.
individuals per year.
Use the Fundamental Theorem of Calculus Part II to verify that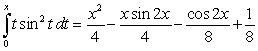 , then find the population after 50 years given that at
, then find the population after 50 years given that at 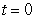 the population was
the population was 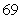 individuals.
individuals.
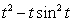 individuals per year.
individuals per year.Use the Fundamental Theorem of Calculus Part II to verify that
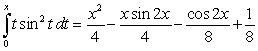 , then find the population after 50 years given that at
, then find the population after 50 years given that at 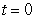 the population was
the population was 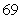 individuals.
individuals.
Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
51
Which of the following is true about 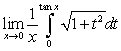
A) It does not exist since the one-sided limits are different.
B) It exists and equals 1.
C) It exists and equals 0.
D) It cannot be computed by L'Hopital's Rule since the conditions for using the rule are not satisfied.
E) It exists and equals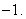
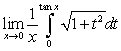
A) It does not exist since the one-sided limits are different.
B) It exists and equals 1.
C) It exists and equals 0.
D) It cannot be computed by L'Hopital's Rule since the conditions for using the rule are not satisfied.
E) It exists and equals
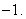

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
52
Two particles start moving from the origin at 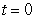 , with velocities
, with velocities 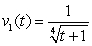 and
and 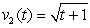 , respectively.
, respectively.
A) What is the distance between the particles at time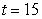 ?
?
B) Will the particles meet again?
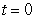 , with velocities
, with velocities 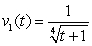 and
and 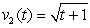 , respectively.
, respectively. A) What is the distance between the particles at time
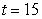 ?
? B) Will the particles meet again?

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
53
The velocity of a turtle is recorded at 1 second intervals (in m/sec). Use the right-endpoint approximation to estimate the total distance the turtle traveled during the 5 seconds recorded. 
0
1
2
3
4
5 .078
.078
0.83
0.75
0.98
0.853
0.425
0
1
2
3
4
5
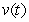 .078
.0780.83
0.75
0.98
0.853
0.425

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
54
Match the function with the derivative: 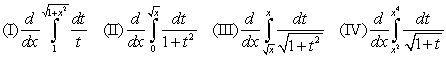
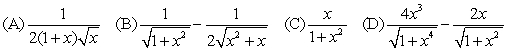 The correct matches are
The correct matches are
A) I-B, II-C, III-D, IV-A
B) I-C, II-A, III-D, IV-B
C) I-A, II-C, III-B, IV-D
D) I-C, II-A, III-B, IV-D
E) None of the above.
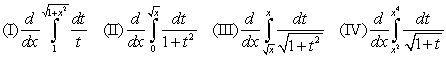
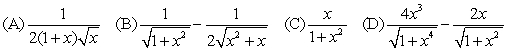 The correct matches are
The correct matches areA) I-B, II-C, III-D, IV-A
B) I-C, II-A, III-D, IV-B
C) I-A, II-C, III-B, IV-D
D) I-C, II-A, III-B, IV-D
E) None of the above.

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
55
Let 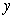 be a twice differentiable function. The integral equation
be a twice differentiable function. The integral equation 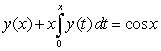 can be written as the following initial value problem:
can be written as the following initial value problem:
A)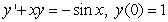
B)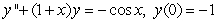
C)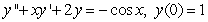
D)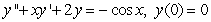
E)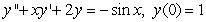
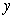 be a twice differentiable function. The integral equation
be a twice differentiable function. The integral equation 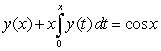 can be written as the following initial value problem:
can be written as the following initial value problem:A)
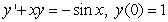
B)
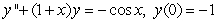
C)
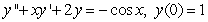
D)
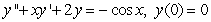
E)
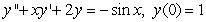

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
56
Let 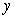 be a twice differentiable function. The integral equation
be a twice differentiable function. The integral equation 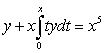 can be rewritten as the following initial value problem:
can be rewritten as the following initial value problem:
A)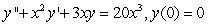
B)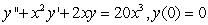
C)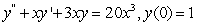
D)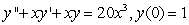
E) None of the above.
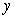 be a twice differentiable function. The integral equation
be a twice differentiable function. The integral equation 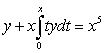 can be rewritten as the following initial value problem:
can be rewritten as the following initial value problem:A)
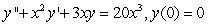
B)
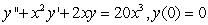
C)
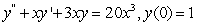
D)
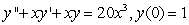
E) None of the above.

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
57
The function 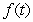 that satisfies the equality
that satisfies the equality 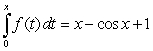 is:
is:
A)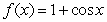
B)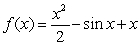
C)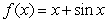
D)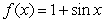
E)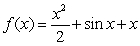
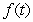 that satisfies the equality
that satisfies the equality 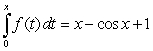 is:
is:A)
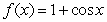
B)
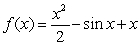
C)
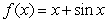
D)
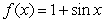
E)
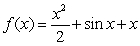

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
58
Let 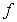 be the function:
be the function: 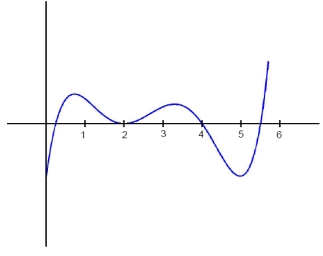 Sketch the graph of the area function
Sketch the graph of the area function 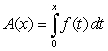 on
on 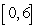 .
.
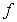 be the function:
be the function:  Sketch the graph of the area function
Sketch the graph of the area function 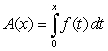 on
on 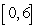 .
.
Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
59
Let 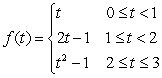 Which of the following functions is the cumulative area function of
Which of the following functions is the cumulative area function of 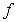 on
on 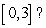
A)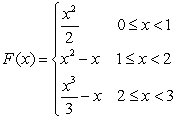
B)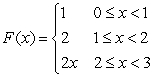
C)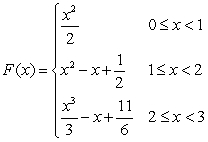
D)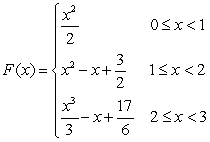
E) None of the above.
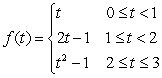 Which of the following functions is the cumulative area function of
Which of the following functions is the cumulative area function of 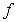 on
on 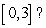
A)
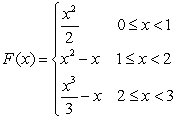
B)
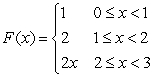
C)
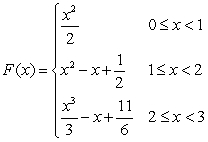
D)
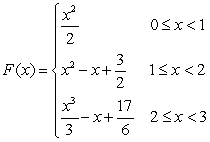
E) None of the above.

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
60
Water flows into a reservoir at a rate of 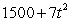 gallons/hour. Since there is a tiny hole in the reservoir, the water leaks out at a rate of
gallons/hour. Since there is a tiny hole in the reservoir, the water leaks out at a rate of 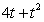 gallons/hour.
gallons/hour.
What is the net change in the amount of water in the reservoir over the time
interval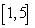 ?
?
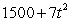 gallons/hour. Since there is a tiny hole in the reservoir, the water leaks out at a rate of
gallons/hour. Since there is a tiny hole in the reservoir, the water leaks out at a rate of 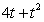 gallons/hour.
gallons/hour.What is the net change in the amount of water in the reservoir over the time
interval
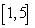 ?
?
Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
61
Find the net change in velocity over 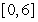 with acceleration
with acceleration 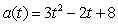 ft/sec2.
ft/sec2.
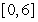 with acceleration
with acceleration 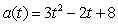 ft/sec2.
ft/sec2.
Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
62
Evaluate the following definite integrals using substitution:
A)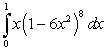
B)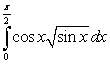
C)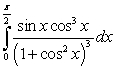
A)
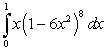
B)
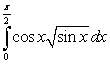
C)
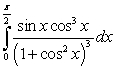

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
63
Evaluate the integral 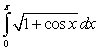 using substitution.
using substitution.
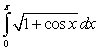 using substitution.
using substitution.
Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
64
Which of the following equalities holds for any two constants 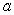 and b?
and b?
A)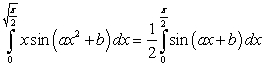
B)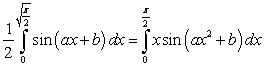
C)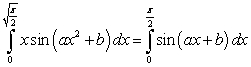
D)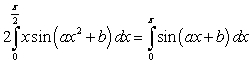
E)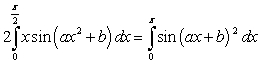
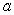 and b?
and b?A)
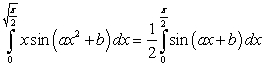
B)
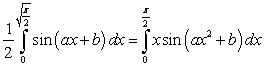
C)
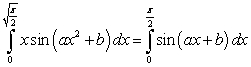
D)
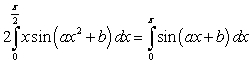
E)
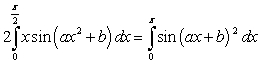

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
65
Find 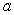 and
and 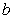 if
if 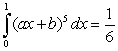 and
and 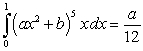 .
.
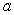 and
and 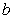 if
if 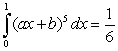 and
and 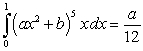 .
.
Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
66
Use the substitution 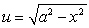 to evaluate the integral
to evaluate the integral 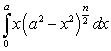 for
for 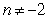 and find
and find 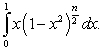
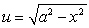 to evaluate the integral
to evaluate the integral 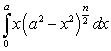 for
for 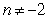 and find
and find 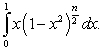

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
67
Evaluate the following definite integrals using the indicated substitution:
A)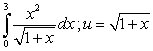
B)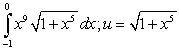
C)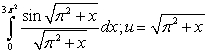
A)
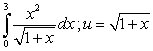
B)
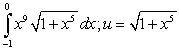
C)
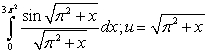

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
68
Use the substitution 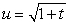 to evaluate the integral
to evaluate the integral 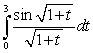 .
.
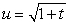 to evaluate the integral
to evaluate the integral 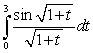 .
.
Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
69
The substitution 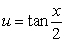 and the identity
and the identity 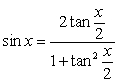 lead to which integration formula?
lead to which integration formula?
A)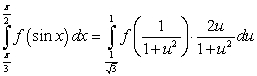
B)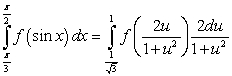
C)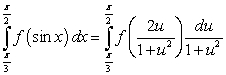
D)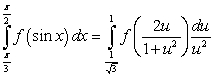
E)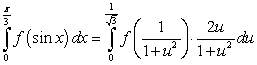
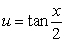 and the identity
and the identity 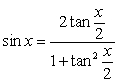 lead to which integration formula?
lead to which integration formula?A)
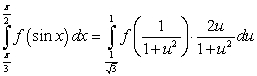
B)
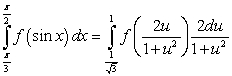
C)
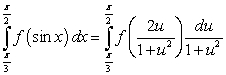
D)
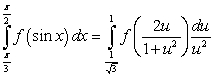
E)
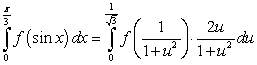

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
70
The substitution 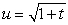 leads to which integration formula?
leads to which integration formula?
A)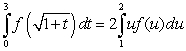
B)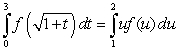
C)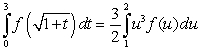
D)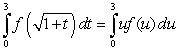
E) None of the above.
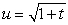 leads to which integration formula?
leads to which integration formula?A)
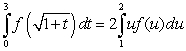
B)
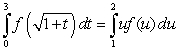
C)
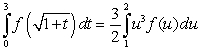
D)
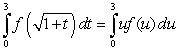
E) None of the above.

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
71
The substitution 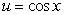 leads to which integration formula?
leads to which integration formula?
A)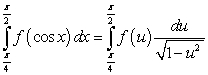
B)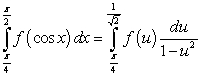
C)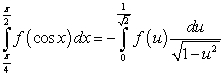
D)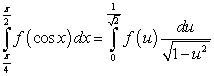
E) None of the above.
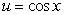 leads to which integration formula?
leads to which integration formula?A)
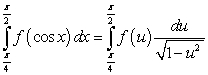
B)
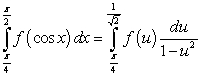
C)
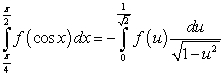
D)
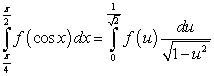
E) None of the above.

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
72
Evaluate the following integrals using the indicated substitution:
A)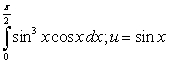
B)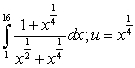
C)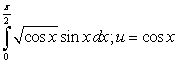
A)
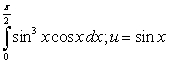
B)
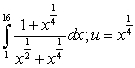
C)
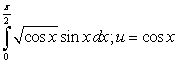

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
73
Use the change of variables formula to evaluate the following definite integrals:
A)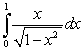
B)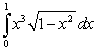
C)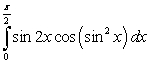
A)
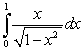
B)
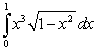
C)
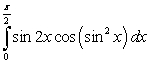

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
74
The substitution 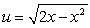 leads to which integration formula below?
leads to which integration formula below?
A)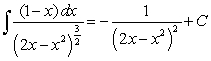
B)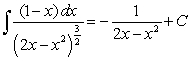
C)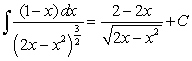
D)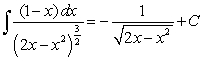
E)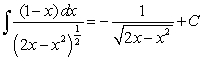
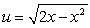 leads to which integration formula below?
leads to which integration formula below?A)
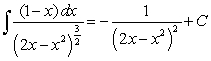
B)
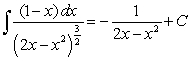
C)
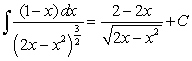
D)
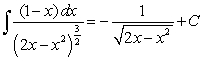
E)
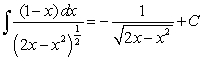

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
75
The current in an electric circuit carries electrons past a certain point at the rate of 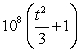 electrons per second (
electrons per second ( 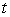 in seconds). How many electrons pass the point from
in seconds). How many electrons pass the point from 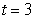 to
to 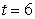 ?
?
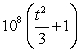 electrons per second (
electrons per second ( 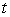 in seconds). How many electrons pass the point from
in seconds). How many electrons pass the point from 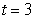 to
to 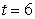 ?
?
Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
76
A particle moves in a straight line with velocity 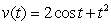 ft/sec. Find the displacement over the interval
ft/sec. Find the displacement over the interval 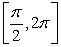 .
.
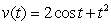 ft/sec. Find the displacement over the interval
ft/sec. Find the displacement over the interval 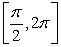 .
.
Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
77
The substitution 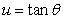 and the identity
and the identity 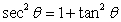 lead to which of the following integration formulas?
lead to which of the following integration formulas?
A)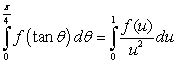
B)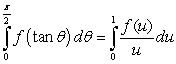
C)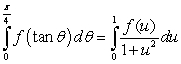
D)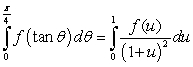
E)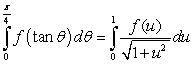
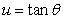 and the identity
and the identity 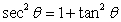 lead to which of the following integration formulas?
lead to which of the following integration formulas?A)
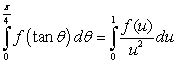
B)
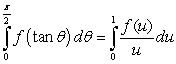
C)
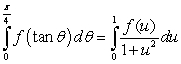
D)
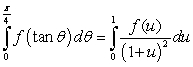
E)
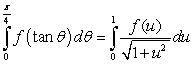

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
78
Evaluate the following integrals:
A)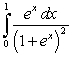
B)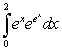
C)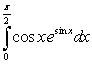
A)
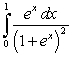
B)
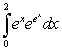
C)
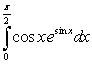

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
79
Compute the integral 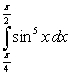 .
.
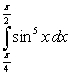 .
.
Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
80
Find the displacement over the time interval 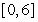 of a car whose velocity is given by
of a car whose velocity is given by 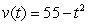 ft/sec.
ft/sec.
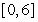 of a car whose velocity is given by
of a car whose velocity is given by 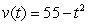 ft/sec.
ft/sec.
Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck


