Deck 9: Random Variables and Probability Distributions
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/28
Play
Full screen (f)
Deck 9: Random Variables and Probability Distributions
1
A shareholder believes that in one year, there is a 20% chance that his stock will be worth $75, a 50% chance that it will be worth $100, and a 30% chance that it will be worth $140.
a. Find the stock's expected value in one year.
b. Find the standard deviation of the stock's worth in one year.
a. Find the stock's expected value in one year.
b. Find the standard deviation of the stock's worth in one year.
a. E(X) = Σ xP(x) = $75(0.20) + $100(0.50) + $140(0.30) = $107
b. σ = SD(X) =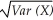 , Var(X) = Σ (x - μ)2 P(x)
, Var(X) = Σ (x - μ)2 P(x)
Var(X) = Σ(x - μ)2 P(x) = (75 - 107)2(0.20) + (100 - 107)2(0.50) + (140 - 107)2(0.30) = 556
σ = SD(X) =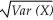 =
= 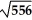 = $23.58
= $23.58
b. σ = SD(X) =
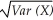 , Var(X) = Σ (x - μ)2 P(x)
, Var(X) = Σ (x - μ)2 P(x)Var(X) = Σ(x - μ)2 P(x) = (75 - 107)2(0.20) + (100 - 107)2(0.50) + (140 - 107)2(0.30) = 556
σ = SD(X) =
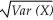 =
= 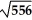 = $23.58
= $23.58 2
The number of plants that are found in a field averages 2 per square metre and follows a Poisson distribution. Based on this,
a. What is the expected value?
b. What is the probability that a 1-square metre section will contain less than 3 plants?
a. What is the expected value?
b. What is the probability that a 1-square metre section will contain less than 3 plants?
a. The expected value of the Poisson distribution is E(X) = λ = 2.
b. P(X < 3) = P(X = 0) + P(X = 1) + P(X = 2) = e-2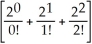 = 0.6767
= 0.6767
b. P(X < 3) = P(X = 0) + P(X = 1) + P(X = 2) = e-2
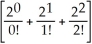 = 0.6767
= 0.6767 3
At a local manufacturing plant, employees must complete new machine set-ups within 30 minutes. New machine set-up times can be described by a Normal model with a mean of 22 minutes and a standard deviation of four minutes.
a. What percent of new machine set-ups take more than 30 minutes?
b. The typical worker needs five minutes to adjust to their surroundings before beginning their duties. What percent of new machine set-ups are completed within 25 minutes to allow for this?
a. What percent of new machine set-ups take more than 30 minutes?
b. The typical worker needs five minutes to adjust to their surroundings before beginning their duties. What percent of new machine set-ups are completed within 25 minutes to allow for this?
a. P(x > 30) = P 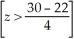 = P(z > 2.00) = 0.0228 = 2.28%
= P(z > 2.00) = 0.0228 = 2.28%
b. P(x ≤ 25) = P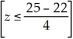 = P(z ≤ 0.75) = 0.7734
= P(z ≤ 0.75) = 0.7734
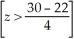 = P(z > 2.00) = 0.0228 = 2.28%
= P(z > 2.00) = 0.0228 = 2.28%b. P(x ≤ 25) = P
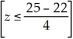 = P(z ≤ 0.75) = 0.7734
= P(z ≤ 0.75) = 0.7734 4
Consider the following to answer the question(s) below:
A company's manufacturing process uses 500 litres of water at a time. A "scrubbing" machine then removes most of a chemical pollutant before pumping the water into a nearby lake. To meet federal regulations the treated water must not contain more than 80 parts per million (ppm) of the chemical. Because there is a fine charged if regulations are not met, the company sets the machine to attain an average of 75 ppm in the treated water. The machine's output can be described by a Normal model with a standard deviation 4.2 ppm.
The company's lawyers insist that not more than 2% of the treated water should be over the limit. In order to achieve this, to what mean should the company set the scrubbing machine? Assume the standard deviation does not change.
A) 75 ppm
B) 78.63 ppm
C) 71.39 ppm
D) 80 ppm
E) 60 ppm
A company's manufacturing process uses 500 litres of water at a time. A "scrubbing" machine then removes most of a chemical pollutant before pumping the water into a nearby lake. To meet federal regulations the treated water must not contain more than 80 parts per million (ppm) of the chemical. Because there is a fine charged if regulations are not met, the company sets the machine to attain an average of 75 ppm in the treated water. The machine's output can be described by a Normal model with a standard deviation 4.2 ppm.
The company's lawyers insist that not more than 2% of the treated water should be over the limit. In order to achieve this, to what mean should the company set the scrubbing machine? Assume the standard deviation does not change.
A) 75 ppm
B) 78.63 ppm
C) 71.39 ppm
D) 80 ppm
E) 60 ppm

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
5
The number of calls received by a call centre follows the Poisson distribution with an average of 5 calls per minute. For a 1 minute period,
a. Find the expected value.
b. Find the probability of receiving no more than 2 calls.
a. Find the expected value.
b. Find the probability of receiving no more than 2 calls.

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
6
Consider the following to answer the question(s) below:
An airline has found that its flights between Toronto and Vancouver can take anywhere from 4.5 to 7.5 hours, with any time between this range being equally likely.
What is the standard deviation?
A) 0.75 hours
B) 0.87 hours
C) 6 hours
D) 0.33 hours
E) 0.5 hours
An airline has found that its flights between Toronto and Vancouver can take anywhere from 4.5 to 7.5 hours, with any time between this range being equally likely.
What is the standard deviation?
A) 0.75 hours
B) 0.87 hours
C) 6 hours
D) 0.33 hours
E) 0.5 hours

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
7
The owner of a small convenience store is trying to decide whether to discontinue selling magazines. He suspects that only 5% of the customers buy magazines and thinks that he might be able to sell something more profitable. Before making a final decision, he keeps track of the number of customers who buy magazines on a given day.
a. On one day, he had 280 customers. Assuming this day was typical, what would be the mean and standard deviation of the number of customers who buy magazines each day?
b. Surprised by the high number of customers who purchased magazines that day, the owner decided that his 5% estimate must have been too low. How many magazine sales would it have taken to convince you? Justify your answer.
a. On one day, he had 280 customers. Assuming this day was typical, what would be the mean and standard deviation of the number of customers who buy magazines each day?
b. Surprised by the high number of customers who purchased magazines that day, the owner decided that his 5% estimate must have been too low. How many magazine sales would it have taken to convince you? Justify your answer.

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
8
Consider the following to answer the question(s) below:
An airline has found that its flights between Toronto and Vancouver can take anywhere from 4.5 to 7.5 hours, with any time between this range being equally likely.
What is the probability that the flight will take more than 7 hours?
A) 0.83
B) 0.33
C) 0.67
D) 0.17
E) 0.99
An airline has found that its flights between Toronto and Vancouver can take anywhere from 4.5 to 7.5 hours, with any time between this range being equally likely.
What is the probability that the flight will take more than 7 hours?
A) 0.83
B) 0.33
C) 0.67
D) 0.17
E) 0.99

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
9
Consider the following to answer the question(s) below:
A courier service claims that only 5 % of all of its deliveries arrive late. Assuming deliveries are independent, a sample of 10 deliveries is randomly selected.
What is the probability that exactly 2 of the sample deliveries arrive late?
A) 0.0746
B) 0.9884
C) 0.2347
D) 0.0439
E) 0.1125
A courier service claims that only 5 % of all of its deliveries arrive late. Assuming deliveries are independent, a sample of 10 deliveries is randomly selected.
What is the probability that exactly 2 of the sample deliveries arrive late?
A) 0.0746
B) 0.9884
C) 0.2347
D) 0.0439
E) 0.1125

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
10
Consider the following to answer the question(s) below:
A company believes that there will be a 50% chance of making a profit of $1,000, a 30% chance of making a profit of $1500 and a 20% chance of making a profit of $2,000.
Find the standard deviation for the company's profit?
A) $390.51
B) $152,498
C) $350
D) $18.71
E) $1,350
A company believes that there will be a 50% chance of making a profit of $1,000, a 30% chance of making a profit of $1500 and a 20% chance of making a profit of $2,000.
Find the standard deviation for the company's profit?
A) $390.51
B) $152,498
C) $350
D) $18.71
E) $1,350

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
11
Consider the following to answer the question(s) below:
At a local manufacturing plant, employees must complete new machine set-ups within 30 minutes. New machine set-up times can be described by a Normal model with a mean of 22 minutes and a standard deviation of four minutes.
The typical worker needs five minutes to adjust to their surroundings before beginning their duties. What percent of new machine set-ups are completed within 25 minutes to allow for this?
A) 77.3%
B) 27.3%
C) 22.7%
D) 72.7%
E) 0.75%
At a local manufacturing plant, employees must complete new machine set-ups within 30 minutes. New machine set-up times can be described by a Normal model with a mean of 22 minutes and a standard deviation of four minutes.
The typical worker needs five minutes to adjust to their surroundings before beginning their duties. What percent of new machine set-ups are completed within 25 minutes to allow for this?
A) 77.3%
B) 27.3%
C) 22.7%
D) 72.7%
E) 0.75%

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
12
Consider the following to answer the question(s) below:
A courier service claims that only 5 % of all of its deliveries arrive late. Assuming deliveries are independent, a sample of 10 deliveries is randomly selected.
What is the probability that more than 2 of the sample deliveries arrive late?
A) 0.0115
B) 0.0105
C) 0.0862
D) 0.0746
E) 0.0439
A courier service claims that only 5 % of all of its deliveries arrive late. Assuming deliveries are independent, a sample of 10 deliveries is randomly selected.
What is the probability that more than 2 of the sample deliveries arrive late?
A) 0.0115
B) 0.0105
C) 0.0862
D) 0.0746
E) 0.0439

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
13
Consider the following to answer the question(s) below:
The number of clients arriving at a bank machine is Poisson distributed with an average of 2 per minute. For a 5 minute period,
What is the probability that no more than 2 customers will arrive in a 5 minute period?
A) 0.0005
B) 0.1246
C) 0.0028
D) 0.6767
E) 0.1353
The number of clients arriving at a bank machine is Poisson distributed with an average of 2 per minute. For a 5 minute period,
What is the probability that no more than 2 customers will arrive in a 5 minute period?
A) 0.0005
B) 0.1246
C) 0.0028
D) 0.6767
E) 0.1353

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
14
Consider the following to answer the question(s) below:
The number of clients arriving at a bank machine is Poisson distributed with an average of 2 per minute. For a 5 minute period,
Find the expected value.
A) 2
B) 1.41
C) 3.16
D) 10
E) 2.24
The number of clients arriving at a bank machine is Poisson distributed with an average of 2 per minute. For a 5 minute period,
Find the expected value.
A) 2
B) 1.41
C) 3.16
D) 10
E) 2.24

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
15
The owner of a pet store is trying to decide whether to discontinue selling specialty clothes for pets. She suspects that only 4% of the customers buy specialty clothes for their pets and thinks that she might be able to replace the clothes with more profitable items. Before making a final decision, she decides to keep track of the total number of customers for a day and whether they purchase specialty clothes.
a. The owner had 275 customers that day. Assuming this was a typical day for her store, what would be the mean and standard deviation of the number of customers who buy specialty clothes for their pet each day?
b. Surprised by the high number of customers who purchased specialty pet clothing that day, the owner decided that her 4% estimate must have been too low. How many clothing sales would it have taken to convince you? Justify your answer.
a. The owner had 275 customers that day. Assuming this was a typical day for her store, what would be the mean and standard deviation of the number of customers who buy specialty clothes for their pet each day?
b. Surprised by the high number of customers who purchased specialty pet clothing that day, the owner decided that her 4% estimate must have been too low. How many clothing sales would it have taken to convince you? Justify your answer.

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
16
A company's manufacturing process uses 500 litres of water at a time. A "scrubbing" machine then removes most of a chemical pollutant before pumping the water into a nearby lake. To meet federal regulations the treated water must not contain more than 80 parts per million (ppm) of the chemical. Because there is a fine charged if regulations are not met, the company sets the machine to attain an average of 75 ppm in the treated water. The machine's output can be described by a Normal model with a standard deviation 4.2 ppm.
a. What percent of the batches of water discharged exceed the 80 ppm standard?
b. The company's lawyers insist that not more than 2% of the treated water should be over the limit. In order to achieve this, to what mean should the company set the scrubbing machine? Assume the standard deviation does not change.
a. What percent of the batches of water discharged exceed the 80 ppm standard?
b. The company's lawyers insist that not more than 2% of the treated water should be over the limit. In order to achieve this, to what mean should the company set the scrubbing machine? Assume the standard deviation does not change.

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
17
Consider the following to answer the question(s) below:
A company believes that there will be a 50% chance of making a profit of $1,000, a 30% chance of making a profit of $1500 and a 20% chance of making a profit of $2,000.
What is the expected profit?
A) $1,000
B) $300
C) $2,000
D) $1,350
E) $4,500
A company believes that there will be a 50% chance of making a profit of $1,000, a 30% chance of making a profit of $1500 and a 20% chance of making a profit of $2,000.
What is the expected profit?
A) $1,000
B) $300
C) $2,000
D) $1,350
E) $4,500

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
18
A company believes that there is a 25% chance of making a daily profit of $500, a 35% chance that it will be $1000 and 40% chance that it will be $1500.
a. Find the expected value.
b. Find the standard deviation.
a. Find the expected value.
b. Find the standard deviation.

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
19
Consider the following to answer the question(s) below:
At a local manufacturing plant, employees must complete new machine set-ups within 30 minutes. New machine set-up times can be described by a Normal model with a mean of 22 minutes and a standard deviation of four minutes.
What percent of new machine set-ups take more than 30 minutes?
A) 97.72%
B) 47.72%
C) 2.28%
D) 52.28%
E) 50%
At a local manufacturing plant, employees must complete new machine set-ups within 30 minutes. New machine set-up times can be described by a Normal model with a mean of 22 minutes and a standard deviation of four minutes.
What percent of new machine set-ups take more than 30 minutes?
A) 97.72%
B) 47.72%
C) 2.28%
D) 52.28%
E) 50%

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
20
Consider the following to answer the question(s) below:
A company's manufacturing process uses 500 litres of water at a time. A "scrubbing" machine then removes most of a chemical pollutant before pumping the water into a nearby lake. To meet federal regulations the treated water must not contain more than 80 parts per million (ppm) of the chemical. Because there is a fine charged if regulations are not met, the company sets the machine to attain an average of 75 ppm in the treated water. The machine's output can be described by a Normal model with a standard deviation 4.2 ppm.
What percent of the batches of water discharged exceed the 80 ppm standard?
A) 88.3%
B) 11.7%
C) 61.7%
D) 38.3%
E) -11.7%
A company's manufacturing process uses 500 litres of water at a time. A "scrubbing" machine then removes most of a chemical pollutant before pumping the water into a nearby lake. To meet federal regulations the treated water must not contain more than 80 parts per million (ppm) of the chemical. Because there is a fine charged if regulations are not met, the company sets the machine to attain an average of 75 ppm in the treated water. The machine's output can be described by a Normal model with a standard deviation 4.2 ppm.
What percent of the batches of water discharged exceed the 80 ppm standard?
A) 88.3%
B) 11.7%
C) 61.7%
D) 38.3%
E) -11.7%

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
21
The city of Halifax has determined that the time between arrivals at a toll booth at the Angus L. Macdonald Bridge is exponentially distributed with λ = 4 cars per minute. Based on this information, what is the probability that the time between any two cars arriving will exceed 11 seconds?
A) about 0.48
B) about 0.52
C) about 0.96
D) about 0.06
E) about 1.0
A) about 0.48
B) about 0.52
C) about 0.96
D) about 0.06
E) about 1.0

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
22
The manager of a computer help desk operation in Moncton has collected enough data to conclude that the time per call is normally distributed with a mean equal to 8.21 minutes and a standard deviation of 2.14 minutes. Based on this, what is the probability that a call will last longer than 13 minutes?
A) 0.0125
B) 0.4875
C) 0.5125
D) 0.9875
E) .0224
A) 0.0125
B) 0.4875
C) 0.5125
D) 0.9875
E) .0224

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
23
Cars arrive randomly and independently at a drive through service centre at a rate of 10 per hour. What is the probability that no cars will arrive in a 15 minute period?
A) 0.0821
B) 0.0067
C) 0.0250
D) 0.00
E) 0.1353
A) 0.0821
B) 0.0067
C) 0.0250
D) 0.00
E) 0.1353

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
24
The manager of a computer help desk operation in Moncton has collected enough data to conclude that the time per call is normally distributed with a mean equal to 8.21 minutes and a standard deviation of 2.14 minutes. What is the probability that three randomly monitored calls will each be completed in 4 minutes or less?
A) about 0.00001
B) about 0.4756
C) about 0.0244
D) about 0.0732
E) about 0.1076
A) about 0.00001
B) about 0.4756
C) about 0.0244
D) about 0.0732
E) about 0.1076

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
25
The probability model for random variable X is specified as: P (X = x) = 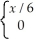
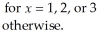 The expected value of X is
The expected value of X is
A) 2.00.
B) 0.50.
C) 0.333.
D) 2.333.
E) 0.167.
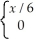
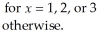 The expected value of X is
The expected value of X isA) 2.00.
B) 0.50.
C) 0.333.
D) 2.333.
E) 0.167.

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
26
It is assumed that the time between failures for an electronic component are exponentially distributed with a mean of 50 hours between consecutive failures. Based on this information, what is the probability that a randomly selected part will fail in less than 10 hours?
A) about 0.18
B) about 0.82
C) about 0.20
D) about 0.002
E) about 0.33
A) about 0.18
B) about 0.82
C) about 0.20
D) about 0.002
E) about 0.33

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
27
Cars arrive randomly and independently at a drive through service centre at a rate of 10 per hour. What is the probability that 2 or 3 cars will arrive in a 15 minute period?
A) 0.4703
B) 0.0131
C) 0.0099
D) 0.2873
E) 0.0053
A) 0.4703
B) 0.0131
C) 0.0099
D) 0.2873
E) 0.0053

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
28
The manager of a computer help desk operation in Moncton has collected enough data to conclude that the time per call is normally distributed with a mean equal to 8.21 minutes and a standard deviation of 2.14 minutes. The manager wants to set the time limit that only 8% of all calls will exceed this limit. The time limit should be
A) about 11.23 minutes.
B) about 5.25 minutes.
C) about 14.58 minutes.
D) about 10.35 minutes.
E) about 20.29 minutes.
A) about 11.23 minutes.
B) about 5.25 minutes.
C) about 14.58 minutes.
D) about 10.35 minutes.
E) about 20.29 minutes.

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck


