Deck 12: Vectors and the Geometry of Space
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/107
Play
Full screen (f)
Deck 12: Vectors and the Geometry of Space
1
Compute ||-4a - 3b||. 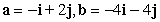
A)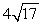
B)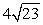
C)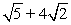
D)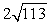
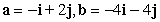
A)
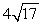
B)
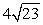
C)
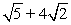
D)
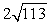
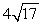
2
Compute -4a - 5b. 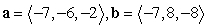
A)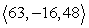
B)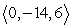
C)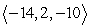
D)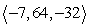
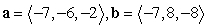
A)
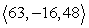
B)
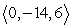
C)
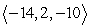
D)
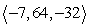
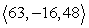
3
Find a vector with the given magnitude in the same direction as the given vector. magnitude 6, v = i - 5j
A) 6i - 30j
B)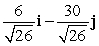
C)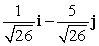
D) 6i
A) 6i - 30j
B)
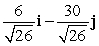
C)
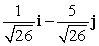
D) 6i
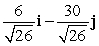
4
Determine whether the vectors a and b are parallel. 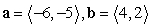
A) parallel
B) not parallel
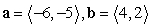
A) parallel
B) not parallel

Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
5
Find a unit vector in the same direction as the given vector. 10i - 2j
A)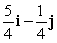
B)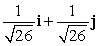
C)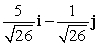
D)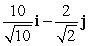
A)
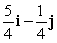
B)
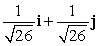
C)
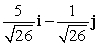
D)
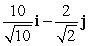

Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
6
Write the given vector as the product of its magnitude and a unit vector. (Write the unit vector so that it is in the same direction as the given vector. This means that the signs of the components of the unit vector should be the same as the signs of the corresponding components of the given vector.) From 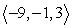 to
to 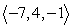
A)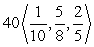
B)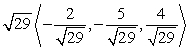
C)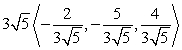
D)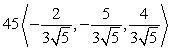
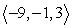 to
to 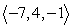
A)
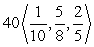
B)
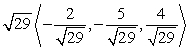
C)
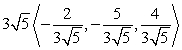
D)
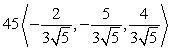

Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
7
Compute 2a - 3b. 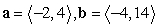
A)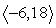
B)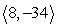
C)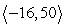
D)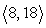
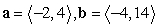
A)
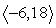
B)
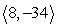
C)
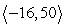
D)
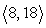

Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
8
The motor of a small boat produces a speed of 2 mph in still water. The boat is travelling in flowing water with a current velocity given by 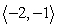 . In what direction should the boat head to travel due east? (Represent the direction with a unit vector.)
. In what direction should the boat head to travel due east? (Represent the direction with a unit vector.)
A) i
B)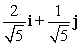
C)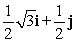
D) The boat cannot travel due east against this current.
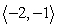 . In what direction should the boat head to travel due east? (Represent the direction with a unit vector.)
. In what direction should the boat head to travel due east? (Represent the direction with a unit vector.)A) i
B)
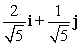
C)
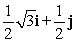
D) The boat cannot travel due east against this current.

Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
9
Compute a + b. 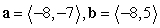
A)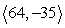
B)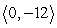
C)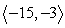
D)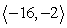
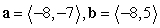
A)
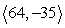
B)
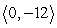
C)
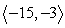
D)
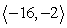

Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
10
Illustrate the difference a - b graphically. a = -i + 4j; b = -3i + 3j 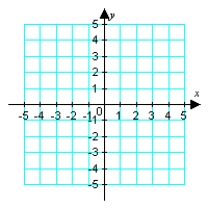
A)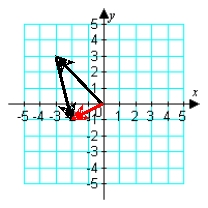
B)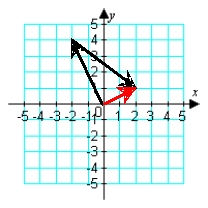
C)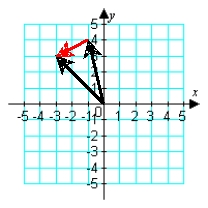
D)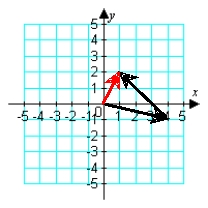

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
11
Find the vector with the given polar form. 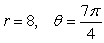
A)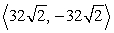
B)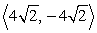
C)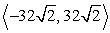
D)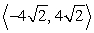
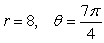
A)
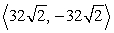
B)
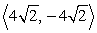
C)
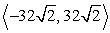
D)
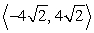

Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
12
Find two unit vectors parallel to the given vector. From 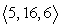 to
to 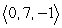
A)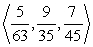
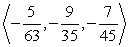
B)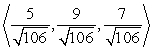
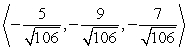
C)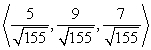
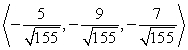
D)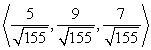
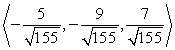
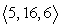 to
to 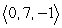
A)
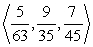
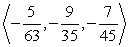
B)
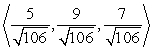
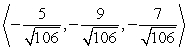
C)
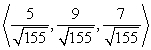
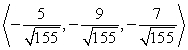
D)
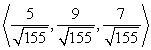
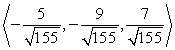

Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
13
Write the given vector as the product of its magnitude and a unit vector. (Write the unit vector so that it is in the same direction as the given vector. This means that the signs of the components of the unit vector should be the same as the signs of the corresponding components of the given vector.) 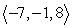
A)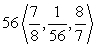
B)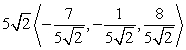
C)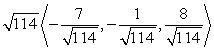
D)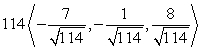
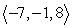
A)
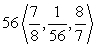
B)
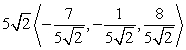
C)
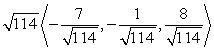
D)
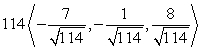

Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
14
Illustrate the sum a + b graphically. a = -2i - j; b = -3i + 2j 
A)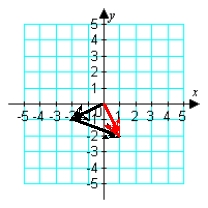
B)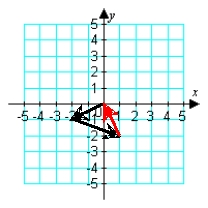
C)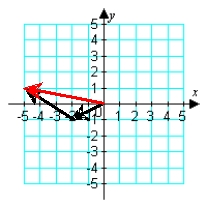
D)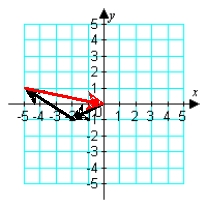

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
15
Compute ||-3a - 2b||. 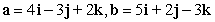
A)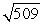
B)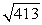
C)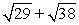
D)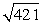
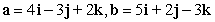
A)
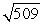
B)
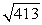
C)
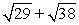
D)
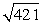

Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
16
Suppose that there are two forces acting on a barge being towed along a river. One force is exerted due south by the river current and has a magnitude of 7 units (the exact nature of the force unit is unimportant). The other force is exerted by a tugboat and has a magnitude of 9 units towards the north and 3 units towards the east. What is the net force acting on the barge?
A) 9 units towards the north, 4 units towards the east
B) 16 units towards the north, 3 units towards the east
C) 2 units towards the north, 3 units towards the east
D) 3 units towards the north, 2 units towards the east
A) 9 units towards the north, 4 units towards the east
B) 16 units towards the north, 3 units towards the east
C) 2 units towards the north, 3 units towards the east
D) 3 units towards the north, 2 units towards the east

Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
17
Find the distance between the given points. (5, -7, 7), (7, 7, 7)
A)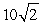
B) 200
C)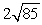
D) 340
A)
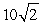
B) 200
C)
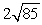
D) 340

Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
18
Determine whether the vectors a and b are parallel. 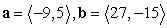
A) parallel
B) not parallel
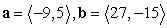
A) parallel
B) not parallel

Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
19
Find two unit vectors parallel to the given vector. 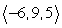
A)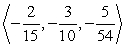
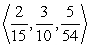
B)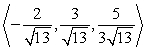
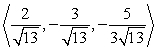
C)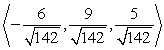
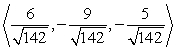
D)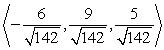
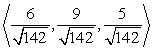
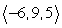
A)
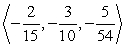
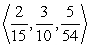
B)
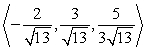
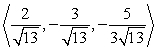
C)
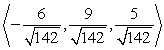
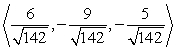
D)
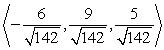
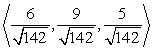

Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
20
Find the vector with initial point A and terminal point B. A = (5, -4), B = (9, 5)
A)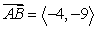
B)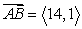
C)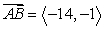
D)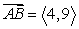
A)
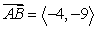
B)
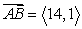
C)
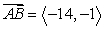
D)
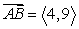

Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
21
Find a vector with the given magnitude and in the same direction as the given vector. Magnitude 2, 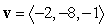
A)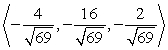
B)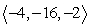
C)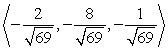
D)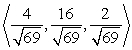
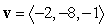
A)
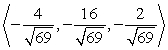
B)
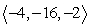
C)
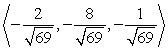
D)
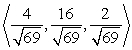

Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
22
Identify the plane as parallel to the xy-plane, xz-plane, or yz-plane. y = -6
A) xz-plane
B) xy-plane
C) yz-plane
D) xy-plane and yz-plane
A) xz-plane
B) xy-plane
C) yz-plane
D) xy-plane and yz-plane

Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
23
Find a vector with the given magnitude and in the same direction as the given vector. Magnitude 6, 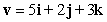
A)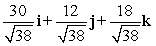
B)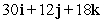
C)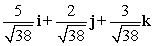
D)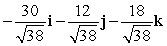
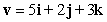
A)
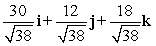
B)
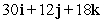
C)
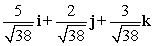
D)
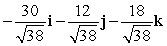

Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
24
Use vectors to determine if the points (5, 30, 7), (3, 3, -2), (-6, 0, 9), and (-4, 27, 18) form a square.
A) yes
B) no
A) yes
B) no

Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
25
Find compb a for the given vectors. 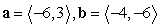
A)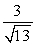
B)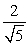
C)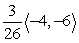
D)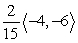
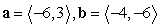
A)
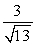
B)
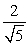
C)
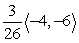
D)
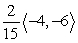

Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
26
Find projb a for the given vectors. 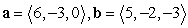
A)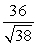
B)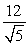
C)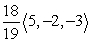
D)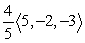
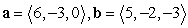
A)
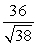
B)
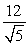
C)
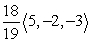
D)
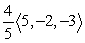

Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
27
Find a vector perpendicular to the given vector. Show all your work. 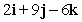
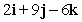

Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
28
Compute 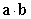 .
. 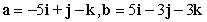
A)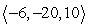
B) -25
C)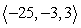
D) 643
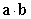 .
. 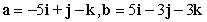
A)
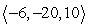
B) -25
C)
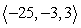
D) 643

Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
29
A small communications satellite is being maneuvered by two on-board thrusters. One thruster generates a force with magnitude 12 newtons in a direction 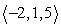 . In response to the applied thrusts, the satellite moves under a total force of
. In response to the applied thrusts, the satellite moves under a total force of 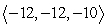 (the components are in units of newtons). Find the thrust vector for the second thruster.
(the components are in units of newtons). Find the thrust vector for the second thruster.
A)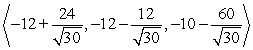
B)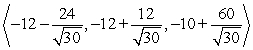
C)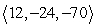
D)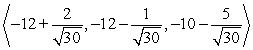
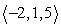 . In response to the applied thrusts, the satellite moves under a total force of
. In response to the applied thrusts, the satellite moves under a total force of 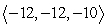 (the components are in units of newtons). Find the thrust vector for the second thruster.
(the components are in units of newtons). Find the thrust vector for the second thruster.A)
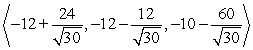
B)
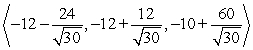
C)
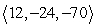
D)
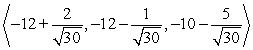

Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
30
Find the displacement vectors 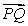 and
and 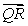 and determine whether the points P = (8, 0, 4), Q = (0, -8, -4), and R = (5, -3, 1) are collinear (on the same line).
and determine whether the points P = (8, 0, 4), Q = (0, -8, -4), and R = (5, -3, 1) are collinear (on the same line).
A) collinear
B) not collinear
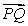 and
and 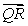 and determine whether the points P = (8, 0, 4), Q = (0, -8, -4), and R = (5, -3, 1) are collinear (on the same line).
and determine whether the points P = (8, 0, 4), Q = (0, -8, -4), and R = (5, -3, 1) are collinear (on the same line).A) collinear
B) not collinear

Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
31
Determine if the vectors are orthogonal. 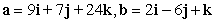
A) orthogonal
B) not orthogonal
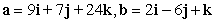
A) orthogonal
B) not orthogonal

Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
32
Find projb a for the given vectors. 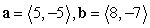
A)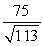
B)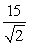
C)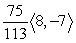
D)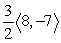
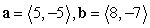
A)
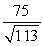
B)
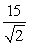
C)
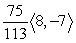
D)
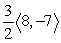

Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
33
Compute 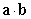 .
. 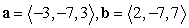
A)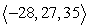
B) 64
C)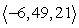
D) 2878
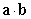 .
. 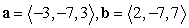
A)
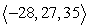
B) 64
C)
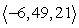
D) 2878

Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
34
Find an equation of the sphere with radius 11 and center (2, -4, 4).
A)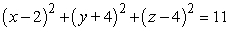
B)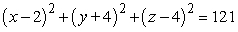
C)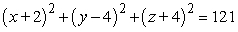
D)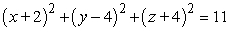
A)
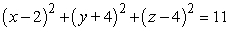
B)
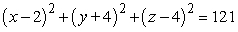
C)
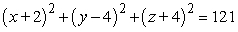
D)
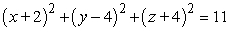

Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
35
A constant force of 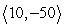 pounds moves an object in a straight line from the point (0, 0) to the point (20, -19). Compute the work done.
pounds moves an object in a straight line from the point (0, 0) to the point (20, -19). Compute the work done.
A) -880
B) 0
C) -750
D) 1150
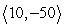 pounds moves an object in a straight line from the point (0, 0) to the point (20, -19). Compute the work done.
pounds moves an object in a straight line from the point (0, 0) to the point (20, -19). Compute the work done.A) -880
B) 0
C) -750
D) 1150

Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
36
Compute the angle between the vectors. Round your answer to two decimal places. 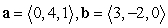
A)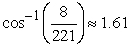
B)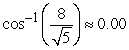
C)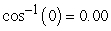
D)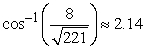
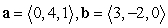
A)
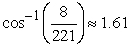
B)
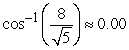
C)
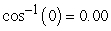
D)
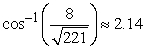

Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
37
Determine if the vectors are orthogonal. 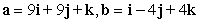
A) orthogonal
B) not orthogonal
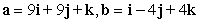
A) orthogonal
B) not orthogonal

Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
38
Compute ||-2a - 3b||. 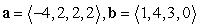
A)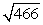
B)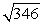
C)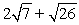
D)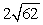
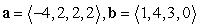
A)
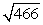
B)
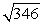
C)
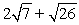
D)
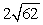

Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
39
Find compb a for the given vectors. 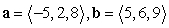
A)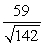
B)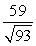
C)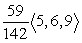
D)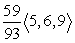
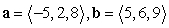
A)
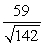
B)
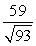
C)
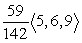
D)
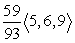

Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
40
Find a vector perpendicular to the given vector. Show all your work. 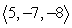
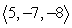

Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
41
If 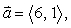 find a vector
find a vector 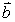 such that
such that 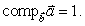
A)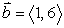
B)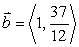
C)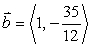
D)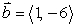
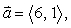 find a vector
find a vector 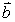 such that
such that 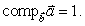
A)
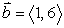
B)
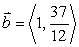
C)
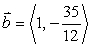
D)
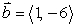

Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
42
Find the indicated area. Area of the parallelogram with two adjacent sides formed by 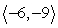 and
and 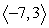
A)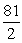
B) 45
C) 81
D)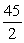
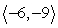 and
and 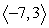
A)
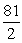
B) 45
C) 81
D)
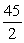

Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
43
Compute the given determinant. 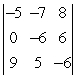
A) -24
B) 4
C) 24
D) -4

A) -24
B) 4
C) 24
D) -4

Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
44
Find two unit vectors orthogonal to the two given vectors. 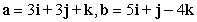
A)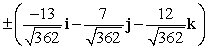
B)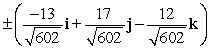
C)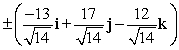
D)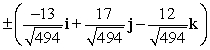
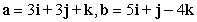
A)
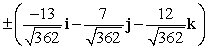
B)
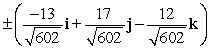
C)
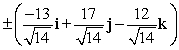
D)
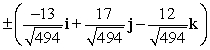

Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
45
Use the cross product to determine the angle betweeen the vectors, assuming that 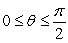 . Round to the nearest thousandth.
. Round to the nearest thousandth. 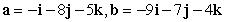
A) 1.571
B) 0.467
C) 0.735
D) 0.835
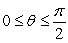 . Round to the nearest thousandth.
. Round to the nearest thousandth. 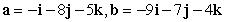
A) 1.571
B) 0.467
C) 0.735
D) 0.835

Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
46
Find two unit vectors orthogonal to the two given vectors. 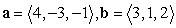
A)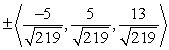
B)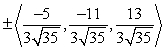
C)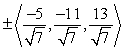
D)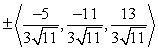
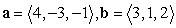
A)
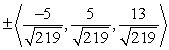
B)
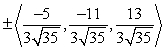
C)
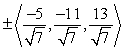
D)
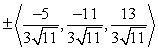

Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
47
Prove that projc(a + b) = projc a + projc b for any non-zero vectors a, b, and c.

Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
48
Use the cross product to determine the angle between the vectors, assuming that 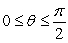 . Round to the nearest thousandth.
. Round to the nearest thousandth. 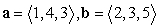
A) 1.571
B) 0.149
C) 0.396
D) 1.175
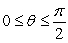 . Round to the nearest thousandth.
. Round to the nearest thousandth. 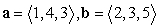
A) 1.571
B) 0.149
C) 0.396
D) 1.175

Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
49
Compute the cross product a × b. 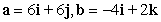
A)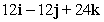
B)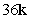
C)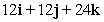
D)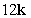
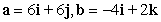
A)
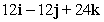
B)
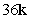
C)
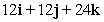
D)
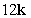

Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
50
Which of the following statements are true? i. 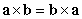 ii.
ii. 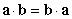 iii.
iii. 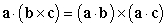
A) i only
B) ii only
C) i and ii only
D) i and iii only
E) iii only
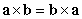 ii.
ii. 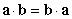 iii.
iii. 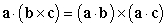
A) i only
B) ii only
C) i and ii only
D) i and iii only
E) iii only

Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
51
Assume that the ball is moving into the page (and away from you) with the indicated spin. Determine the direction of the Magnus force. 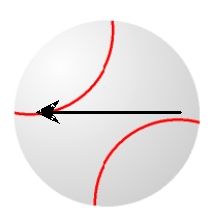
A) to the right
B) to the left
C) up
D) down
E) The Magnus force is zero.

A) to the right
B) to the left
C) up
D) down
E) The Magnus force is zero.

Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
52
Find the indicated area. Area of the triangle with vertices 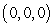 ,
, 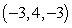 , and
, and 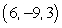
A)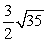
B)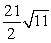
C)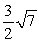
D)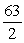
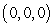 ,
, 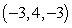 , and
, and 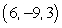
A)
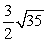
B)
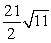
C)
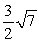
D)
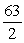

Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
53
Assume that the ball is moving into the page (and away from you) with the indicated spin. Determine the direction of the Magnus force. 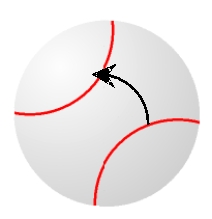
A) to the right
B) to the left
C) up
D) down
E) The Magnus force is zero.

A) to the right
B) to the left
C) up
D) down
E) The Magnus force is zero.

Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
54
A constant force of ![<strong>A constant force of pounds moves an object in a straight line a distance of 15 feet, and the work done is 110 ft-lb. If the motion of the object started at the point (0, 0), find the coordinates of the final position of the object. [Assume that the final position is somewhere in the first quadrant of the coordinate system.]</strong> A) B) C) D) The final position cannot be determined.](https://storage.examlex.com/TB5869/11eaa88b_93aa_dc13_a696_ab8261395acf_TB5869_11.jpg) pounds moves an object in a straight line a distance of 15 feet, and the work done is 110 ft-lb. If the motion of the object started at the point (0, 0), find the coordinates of the final position of the object. [Assume that the final position is somewhere in the first quadrant of the coordinate system.]
pounds moves an object in a straight line a distance of 15 feet, and the work done is 110 ft-lb. If the motion of the object started at the point (0, 0), find the coordinates of the final position of the object. [Assume that the final position is somewhere in the first quadrant of the coordinate system.]
A)![<strong>A constant force of pounds moves an object in a straight line a distance of 15 feet, and the work done is 110 ft-lb. If the motion of the object started at the point (0, 0), find the coordinates of the final position of the object. [Assume that the final position is somewhere in the first quadrant of the coordinate system.]</strong> A) B) C) D) The final position cannot be determined.](https://storage.examlex.com/TB5869/11eaa88b_93ab_0324_a696_b18fb8e07445_TB5869_11.jpg)
B)![<strong>A constant force of pounds moves an object in a straight line a distance of 15 feet, and the work done is 110 ft-lb. If the motion of the object started at the point (0, 0), find the coordinates of the final position of the object. [Assume that the final position is somewhere in the first quadrant of the coordinate system.]</strong> A) B) C) D) The final position cannot be determined.](https://storage.examlex.com/TB5869/11eaa88b_93ab_2a35_a696_c39a68cc0f79_TB5869_11.jpg)
C)![<strong>A constant force of pounds moves an object in a straight line a distance of 15 feet, and the work done is 110 ft-lb. If the motion of the object started at the point (0, 0), find the coordinates of the final position of the object. [Assume that the final position is somewhere in the first quadrant of the coordinate system.]</strong> A) B) C) D) The final position cannot be determined.](https://storage.examlex.com/TB5869/11eaa88b_93ab_2a36_a696_e505fbc19acd_TB5869_11.jpg)
D) The final position cannot be determined.
![<strong>A constant force of pounds moves an object in a straight line a distance of 15 feet, and the work done is 110 ft-lb. If the motion of the object started at the point (0, 0), find the coordinates of the final position of the object. [Assume that the final position is somewhere in the first quadrant of the coordinate system.]</strong> A) B) C) D) The final position cannot be determined.](https://storage.examlex.com/TB5869/11eaa88b_93aa_dc13_a696_ab8261395acf_TB5869_11.jpg) pounds moves an object in a straight line a distance of 15 feet, and the work done is 110 ft-lb. If the motion of the object started at the point (0, 0), find the coordinates of the final position of the object. [Assume that the final position is somewhere in the first quadrant of the coordinate system.]
pounds moves an object in a straight line a distance of 15 feet, and the work done is 110 ft-lb. If the motion of the object started at the point (0, 0), find the coordinates of the final position of the object. [Assume that the final position is somewhere in the first quadrant of the coordinate system.]A)
![<strong>A constant force of pounds moves an object in a straight line a distance of 15 feet, and the work done is 110 ft-lb. If the motion of the object started at the point (0, 0), find the coordinates of the final position of the object. [Assume that the final position is somewhere in the first quadrant of the coordinate system.]</strong> A) B) C) D) The final position cannot be determined.](https://storage.examlex.com/TB5869/11eaa88b_93ab_0324_a696_b18fb8e07445_TB5869_11.jpg)
B)
![<strong>A constant force of pounds moves an object in a straight line a distance of 15 feet, and the work done is 110 ft-lb. If the motion of the object started at the point (0, 0), find the coordinates of the final position of the object. [Assume that the final position is somewhere in the first quadrant of the coordinate system.]</strong> A) B) C) D) The final position cannot be determined.](https://storage.examlex.com/TB5869/11eaa88b_93ab_2a35_a696_c39a68cc0f79_TB5869_11.jpg)
C)
![<strong>A constant force of pounds moves an object in a straight line a distance of 15 feet, and the work done is 110 ft-lb. If the motion of the object started at the point (0, 0), find the coordinates of the final position of the object. [Assume that the final position is somewhere in the first quadrant of the coordinate system.]</strong> A) B) C) D) The final position cannot be determined.](https://storage.examlex.com/TB5869/11eaa88b_93ab_2a36_a696_e505fbc19acd_TB5869_11.jpg)
D) The final position cannot be determined.

Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
55
Compute the cross product a × b. 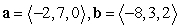
A)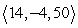
B)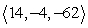
C)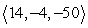
D)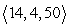
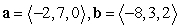
A)
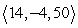
B)
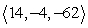
C)
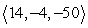
D)
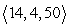

Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
56
Use the Cauchy-Schwartz Inequality in n dimensions to show that 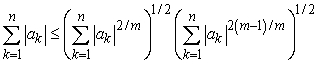 ,
,
where m is an odd natural number.
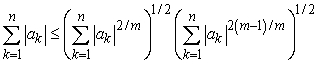 ,
,where m is an odd natural number.

Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
57
Who is doing more work: a weight lifter who is holding a 450-pound barbell motionless over his head, or senior citizen sitting on a park bench? Explain.

Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
58
If you apply a force of magnitude 39 pounds at the end of an 9-inch wrench at an angle of 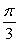 to the wrench, find the magnitude of the torque applied to the bolt. Round to the nearest tenth of an inch-pound.
to the wrench, find the magnitude of the torque applied to the bolt. Round to the nearest tenth of an inch-pound.
A) 25.3 in-lb
B) 175.5 in-lb
C) 14.6 in-lb
D) 304.0 in-lb
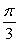 to the wrench, find the magnitude of the torque applied to the bolt. Round to the nearest tenth of an inch-pound.
to the wrench, find the magnitude of the torque applied to the bolt. Round to the nearest tenth of an inch-pound.A) 25.3 in-lb
B) 175.5 in-lb
C) 14.6 in-lb
D) 304.0 in-lb

Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
59
Find the indicated volume. Volume of the parallelpiped with three adjacent edges formed by 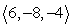 ,
, 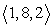 , and
, and 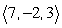
A) 232
B)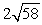
C)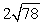
D) 312
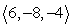 ,
, 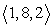 , and
, and 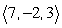
A) 232
B)
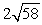
C)
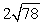
D) 312

Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
60
Find the distance from the point Q to the given line. Round to the nearest thousandth. 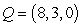 , line through
, line through 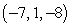 and
and 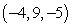
A) 17.117
B) 1.018
C) 17.647
D) 14.314
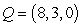 , line through
, line through 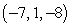 and
and 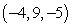
A) 17.117
B) 1.018
C) 17.647
D) 14.314

Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
61
Find parametric equations of the line through 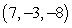 parallel to
parallel to 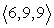 .
.
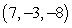 parallel to
parallel to 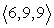 .
.
Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
62
Find symmetric equations of the line through 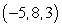 and normal to the plane
and normal to the plane 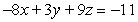 .
.
A)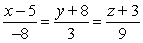
B)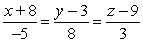
C)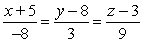
D)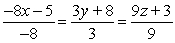
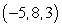 and normal to the plane
and normal to the plane 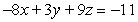 .
.A)
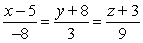
B)
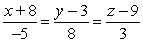
C)
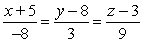
D)
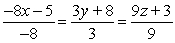

Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
63
Find symmetric equations of the line through 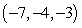 and
and 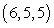 .
.
A)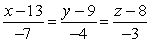
B)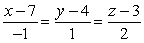
C)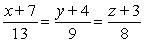
D)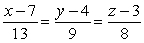
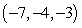 and
and 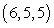 .
.A)
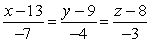
B)
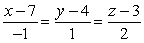
C)
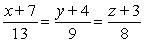
D)
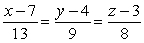

Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
64
Use the parallelpiped volume formula to determine if the vectors are coplanar. 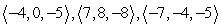
A) coplanar
B) not coplanar
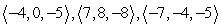
A) coplanar
B) not coplanar

Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
65
Determine if the lines are parallel, skew or intersect. 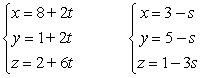
A) parallel
B) skew
C) intersect
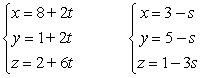
A) parallel
B) skew
C) intersect

Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
66
Use geometry to identify the cross product. 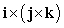
A) 0
B) j
C) k
D) -i
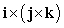
A) 0
B) j
C) k
D) -i

Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
67
Find symmetric equations of the line through 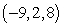 and parallel to
and parallel to 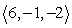 .
.
A)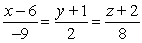
B)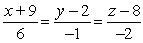
C)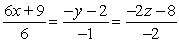
D)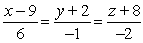
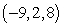 and parallel to
and parallel to 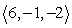 .
.A)
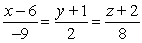
B)
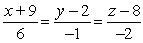
C)
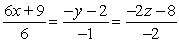
D)
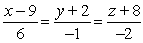

Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
68
Determine if the lines are parallel, skew or intersect. 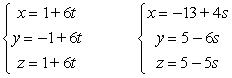
A) parallel
B) skew
C) intersect
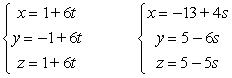
A) parallel
B) skew
C) intersect

Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
69
Find an equation of the given plane. The plane containing the point 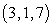 with normal vector
with normal vector 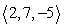
A) 3x + y + 7z = -22
B) 2x + 7y - 5z = 0
C) 2x + 7y - 5z = -22
D) 2x + 7y - 5z = 11
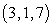 with normal vector
with normal vector 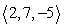
A) 3x + y + 7z = -22
B) 2x + 7y - 5z = 0
C) 2x + 7y - 5z = -22
D) 2x + 7y - 5z = 11

Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
70
Use the parallelpiped volume formula to determine if the vectors are coplanar. 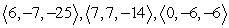
A) coplanar
B) not coplanar
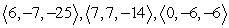
A) coplanar
B) not coplanar

Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
71
Determine if the lines are parallel, skew or intersect. 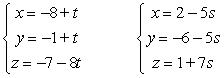
A) parallel
B) skew
C) intersect
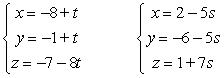
A) parallel
B) skew
C) intersect

Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
72
Sketch the given plane. y + 2z = 6 
A)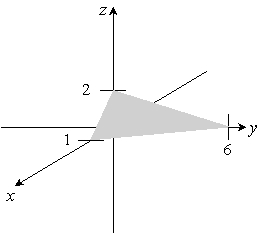
B)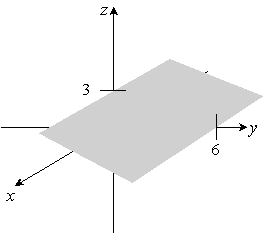
C)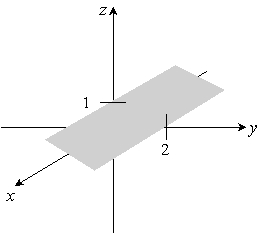
D)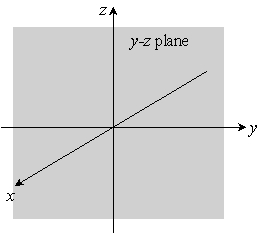

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
73
Sketch the given plane. 3x - y + 2z = 6 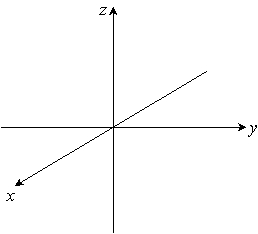
A)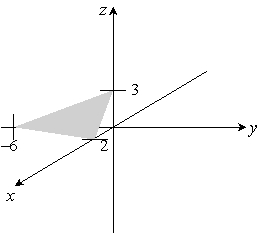
B)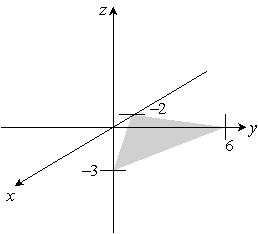
C)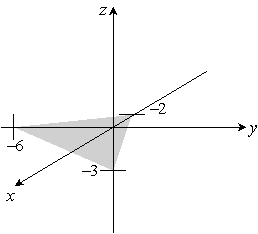
D)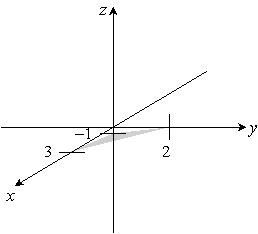

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
74
In many farmers' barns and in many mechanics' shops, you can find a stout steel pipe about 2 to 3 feet in length with one end pinched so that the pinched end fits snugly over a wrench handle. What might explain the common presence of this object in these settings? Explain your answer in terms of the vector concepts you have learned.

Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
75
Find an equation of the given plane. The plane containing the points 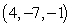 ,
, 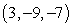 and
and 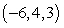
A) 3x - 9y - 7z = 82
B) 9x - 13y - 10z = 137
C) 9x - 13y - 10z = 0
D) 58x + 64y - 31z = -185
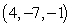 ,
, 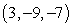 and
and 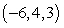
A) 3x - 9y - 7z = 82
B) 9x - 13y - 10z = 137
C) 9x - 13y - 10z = 0
D) 58x + 64y - 31z = -185

Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
76
Find an equation of the given plane. The plane containing the point 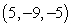 and perpendicular to the planes 7x + y - z = -5 and x - 6y - 4z = -3
and perpendicular to the planes 7x + y - z = -5 and x - 6y - 4z = -3
A) -10x + 27y - 43z = -9
B) -10x + 27y - 43z = -78
C) 7x + y - z = 31
D) -10x + 27y - 43z = 416
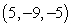 and perpendicular to the planes 7x + y - z = -5 and x - 6y - 4z = -3
and perpendicular to the planes 7x + y - z = -5 and x - 6y - 4z = -3A) -10x + 27y - 43z = -9
B) -10x + 27y - 43z = -78
C) 7x + y - z = 31
D) -10x + 27y - 43z = 416

Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
77
Show that 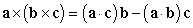 . Show all of your work.
. Show all of your work.
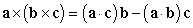 . Show all of your work.
. Show all of your work.
Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
78
Find parametric equations of the line through 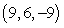 and perpendicular to both
and perpendicular to both 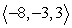 and
and 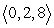 .
.
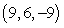 and perpendicular to both
and perpendicular to both 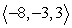 and
and 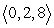 .
.
Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
79
Find parametric equations of the line through 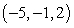 and
and 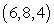 .
.
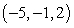 and
and 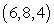 .
.
Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
80
Use geometry to identify the cross product. 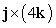
A) -4j
B) 0
C) 4i
D) 4k
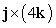
A) -4j
B) 0
C) 4i
D) 4k

Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck


