Deck 6: Applications of the Definite Integral
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/85
Play
Full screen (f)
Deck 6: Applications of the Definite Integral
1
Identify the graph and area of the region bounded by the curves 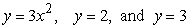 . Use only one integral. The figures below are not necessarily to scale.
. Use only one integral. The figures below are not necessarily to scale.
A)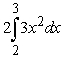
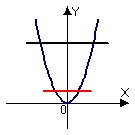
B)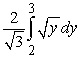
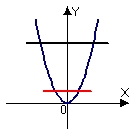
C)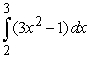

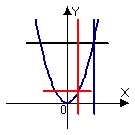
D)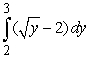
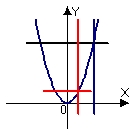
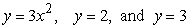 . Use only one integral. The figures below are not necessarily to scale.
. Use only one integral. The figures below are not necessarily to scale.A)
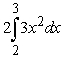

B)
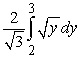

C)
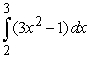


D)
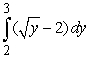

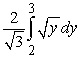

2
A 2-person tent has a rectangular base 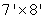 and rises to a single point 5' up. Compute the volume of the tent.
and rises to a single point 5' up. Compute the volume of the tent. 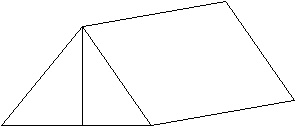 7 ft 8 ft
7 ft 8 ft
A) 75 ft3
B) 70 ft3
C) 140 ft3
D) 280 ft3
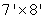 and rises to a single point 5' up. Compute the volume of the tent.
and rises to a single point 5' up. Compute the volume of the tent.  7 ft 8 ft
7 ft 8 ftA) 75 ft3
B) 70 ft3
C) 140 ft3
D) 280 ft3
140 ft3
3
Identify the graph and the area bounded by the curves 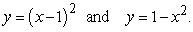
A) area = 5/3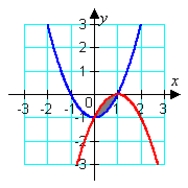
B) area = 1/6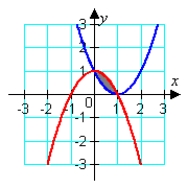
C) area = 1/3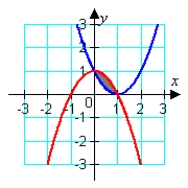
D) area = 1/3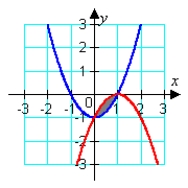
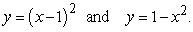
A) area = 5/3

B) area = 1/6

C) area = 1/3

D) area = 1/3

area = 1/3 

4
Find the area between the curves on the given interval. y = x4, y = x - 1, -1 x 1
A)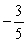
B)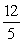
C)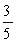
D)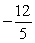
A)
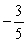
B)
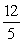
C)
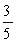
D)
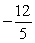

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
5
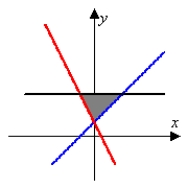
Identify the graph and area of the region bounded by the curves 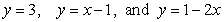 . The figures below are not necessarily to scale.
. The figures below are not necessarily to scale.
A) area =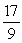
B) area =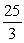
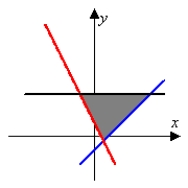
C) area =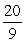
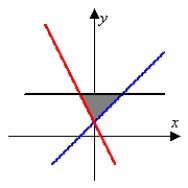
D) area =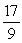
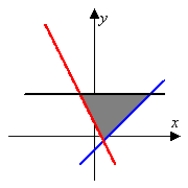
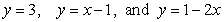 . The figures below are not necessarily to scale.
. The figures below are not necessarily to scale.A) area =
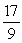

B) area =
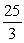

C) area =
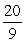

D) area =
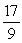


Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
6
Estimate the intersection points to the nearest tenth then use these points to estimate the area. 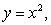
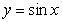
A) area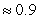
B) area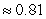
C) area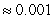
D) area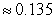
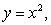
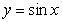
A) area
B) area
C) area
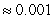
D) area
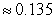

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
7
Find the volume of the solid with cross-sectional area 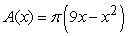 extending over the range
extending over the range 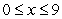 .
.
A)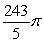
B)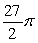
C)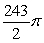
D)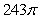
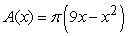 extending over the range
extending over the range 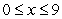 .
.A)
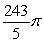
B)
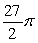
C)
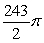
D)
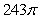

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
8
Compute the volume of the solid formed by revolving the region bounded by 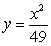 and
and 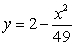 about the x-axis.
about the x-axis.
A)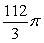
B)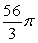
C)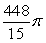
D)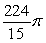
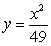 and
and 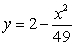 about the x-axis.
about the x-axis.A)
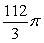
B)
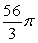
C)
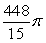
D)
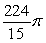

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
9
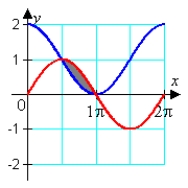
Identify the graph and the area bounded by the curves 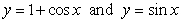 on the interval
on the interval 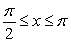 .
.
A)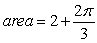
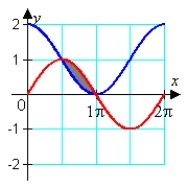
B)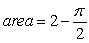
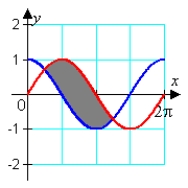
C)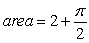
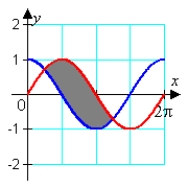
D)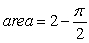
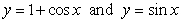 on the interval
on the interval 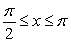 .
.A)
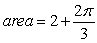

B)
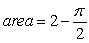

C)
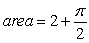

D)
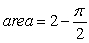


Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
10
Find the volume of the solid with cross-sectional area 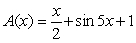 extending over the range
extending over the range 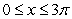 .
.
A)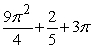
B)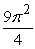
C)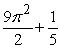
D)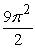
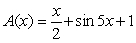 extending over the range
extending over the range 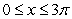 .
.A)
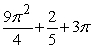
B)
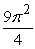
C)
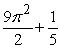
D)
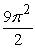

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
11
Find the area between the following curves on the given interval. 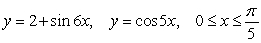
A)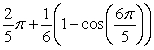
B)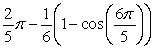

C)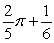
D)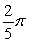
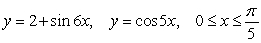
A)
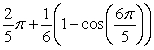
B)
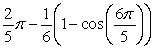

C)
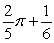
D)
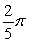

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
12
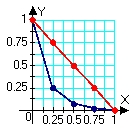
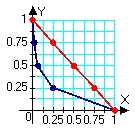
Identify the graph and the area of the region determined by the intersections of the tabulated curves using Simpson's Rule. x
0)00
0)25
0)50
0)75
1)00
F1(x)
1)0
0)25
0)07
0)02
0)00
F2(x)
1)0
0)75
0)50
0)25
0)00
A)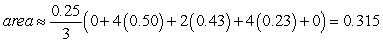
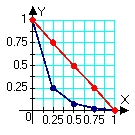
B)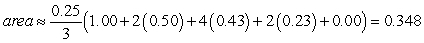
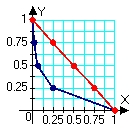
C)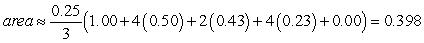
D)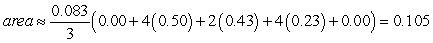
0)00
0)25
0)50
0)75
1)00
F1(x)
1)0
0)25
0)07
0)02
0)00
F2(x)
1)0
0)75
0)50
0)25
0)00
A)
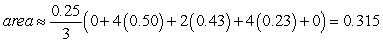

B)
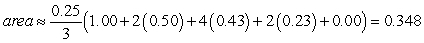

C)
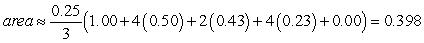

D)
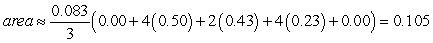


Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
13
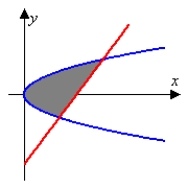
Identify the graph and area of the region bounded by the curves 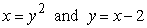 . Use only one integral. The figures below are not necessarily to scale.
. Use only one integral. The figures below are not necessarily to scale.
A)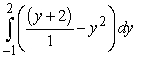
B)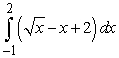
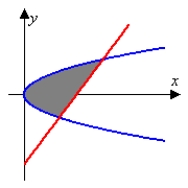
C)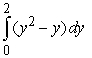
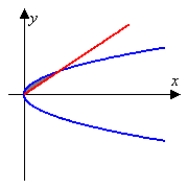
D)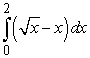
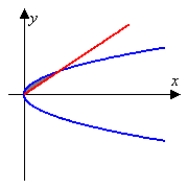
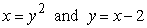 . Use only one integral. The figures below are not necessarily to scale.
. Use only one integral. The figures below are not necessarily to scale.A)
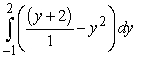

B)
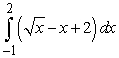

C)
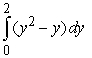

D)
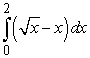


Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
14
Find the area of the region determined by the intersections of the curves. 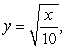
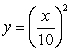
A) 10
B) 20
C)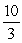
D)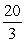
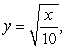
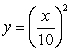
A) 10
B) 20
C)
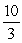
D)
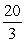

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
15
Find the area between the following curves on the given interval. 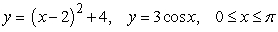
A)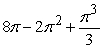
B)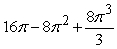
C)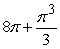
D)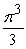
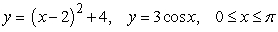
A)
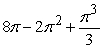
B)
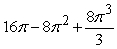
C)
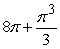
D)
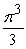

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
16
Find the area of the region bounded by the given curves. Write a single integral that represents the area. 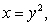
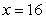
A) area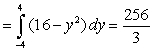
B) area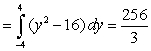
C) area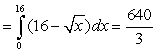
D) area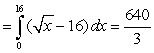
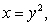
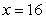
A) area
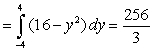
B) area
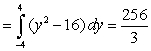
C) area
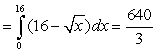
D) area
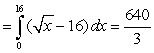

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
17
Use Simpson's rule to estimate the volume from the given cross sectional areas. x(cm)
-1)0
-0)5
0)0
0)5
1)0
A(x) (cm2)
1)4
1)5
2)0
2)5
2)6
A) 3.3
B) 4.0
C) 12.0
D) 6.0
-1)0
-0)5
0)0
0)5
1)0
A(x) (cm2)
1)4
1)5
2)0
2)5
2)6
A) 3.3
B) 4.0
C) 12.0
D) 6.0

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
18
A football (American) has a circular cross section with radius approximately 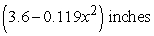 for
for 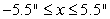 . Compute the volume of the football.
. Compute the volume of the football.
A) 238.9 inches3
B) 165.9 inches3
C) 119.4 inches3
D) 82.9 inches3
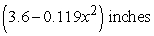 for
for 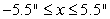 . Compute the volume of the football.
. Compute the volume of the football.A) 238.9 inches3
B) 165.9 inches3
C) 119.4 inches3
D) 82.9 inches3

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
19
Compute the volume of a solid formed by revolving the region bounded by 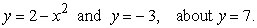
A)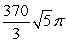
B)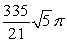
C)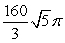
D)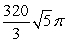
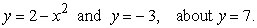
A)
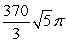
B)
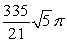
C)
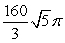
D)
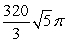

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
20
Given a certain amount of land potentially devoted to farming, one will first use the more fertile regions where production costs are lowest before using the less fertile regions. The consequence of this logical strategy is that the production costs increase as production increases. A certain landowner has enough land to produce 106 bushels of a particular crop, and the production costs, c, of the nth bushel is described with the equation 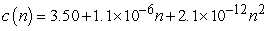 . If the market price is p for this particular crop, the profit for producing the nth bushel is
. If the market price is p for this particular crop, the profit for producing the nth bushel is 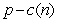 . If p = $5.25, how much total profit could the farmer expect to obtain by producing
. If p = $5.25, how much total profit could the farmer expect to obtain by producing 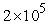 bushels.
bushels.
A) $377,600
B) $289,200
C) $350,000
D) $322,400
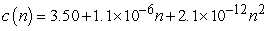 . If the market price is p for this particular crop, the profit for producing the nth bushel is
. If the market price is p for this particular crop, the profit for producing the nth bushel is 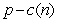 . If p = $5.25, how much total profit could the farmer expect to obtain by producing
. If p = $5.25, how much total profit could the farmer expect to obtain by producing 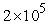 bushels.
bushels.A) $377,600
B) $289,200
C) $350,000
D) $322,400

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
21
Use the best method available to find the volume of the solid formed by revolving the region bounded by 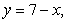
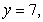 and
and 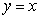 about the x-axis. Write the integral that is used to find the volume.
about the x-axis. Write the integral that is used to find the volume.
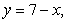
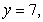 and
and 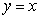 about the x-axis. Write the integral that is used to find the volume.
about the x-axis. Write the integral that is used to find the volume.
Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
22
Use cylindrical shells to compute the volume of the solid formed by revolving the region bounded by 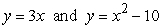 about x = 5.
about x = 5.
A)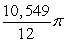
B)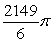
C)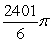
D)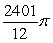
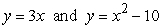 about x = 5.
about x = 5.A)
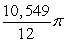
B)
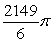
C)
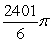
D)
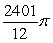

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
23
Use the best method available to find the volume of the solid formed by revolving the region bounded by the y-axis, 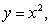
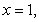 and
and 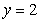 about the y-axis. Write the integral that is used to find the volume.
about the y-axis. Write the integral that is used to find the volume.
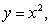
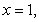 and
and 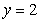 about the y-axis. Write the integral that is used to find the volume.
about the y-axis. Write the integral that is used to find the volume.
Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
24
Show that the volume of a solid formed by revolving the region bounded by x = y2 and x = r about x = r is 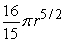 .
.
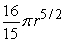 .
.
Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
25
Use cylindrical shells to compute the volume of the solid formed by revolving the region bounded by 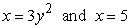 about y = 10.
about y = 10.
A)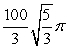
B)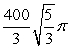
C)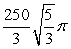
D)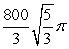
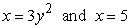 about y = 10.
about y = 10.A)
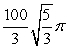
B)
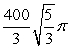
C)
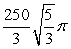
D)
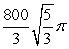

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
26
Use Simpson's Rule to estimate the volume of the shape obtained by revolving the cross-section given in the table about the y-axis. y
0
0)4375
0)75
0)9375
1
0)9375
0)75
0)4375
0
X
1
1)25
1)5
1)75
2
2)25
2)5
2)75
3
A) 3
B) 17
C) 24
D) 26
0
0)4375
0)75
0)9375
1
0)9375
0)75
0)4375
0
X
1
1)25
1)5
1)75
2
2)25
2)5
2)75
3
A) 3
B) 17
C) 24
D) 26

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
27
Find the volume of the solid formed by revolving the region bounded by 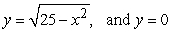 about y = 0.
about y = 0.
A)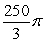
B)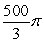
C)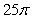
D)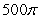
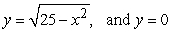 about y = 0.
about y = 0.A)
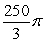
B)
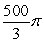
C)
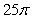
D)
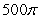

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
28
Let R be the region bounded by 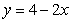 , the x-axis, and the y-axis. Compute the volume of the solid formed by revolving R about the y-axis.
, the x-axis, and the y-axis. Compute the volume of the solid formed by revolving R about the y-axis.
A)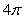
B)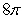
C)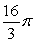
D)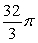
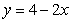 , the x-axis, and the y-axis. Compute the volume of the solid formed by revolving R about the y-axis.
, the x-axis, and the y-axis. Compute the volume of the solid formed by revolving R about the y-axis.A)
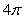
B)
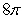
C)
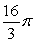
D)
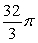

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
29
Let R be the region bounded by 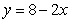 , the x-axis, and the y-axis. Compute the volume of the solid formed by revolving R about the x-axis.
, the x-axis, and the y-axis. Compute the volume of the solid formed by revolving R about the x-axis.
A)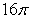
B)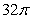
C)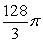
D)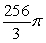
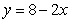 , the x-axis, and the y-axis. Compute the volume of the solid formed by revolving R about the x-axis.
, the x-axis, and the y-axis. Compute the volume of the solid formed by revolving R about the x-axis.A)
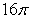
B)
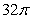
C)
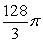
D)
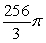

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
30
The base of a solid V is the region bounded by 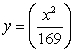 and
and 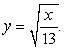 Find the volume if V has square cross sections.
Find the volume if V has square cross sections.
A)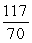
B)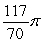
C)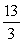
D)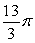
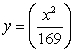 and
and 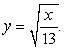 Find the volume if V has square cross sections.
Find the volume if V has square cross sections.A)
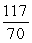
B)
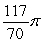
C)
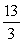
D)
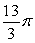

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
31
Find the volume of the solid formed by revolving the region bounded by 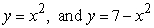 about x = 8.
about x = 8.
A)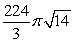
B)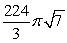
C)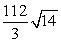
D)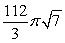
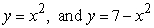 about x = 8.
about x = 8.A)
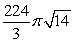
B)
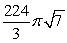
C)
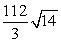
D)
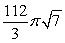

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
32
Use the best method available to find the volume of the solid formed by revolving the region bounded by 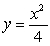 and
and 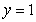 about the x-axis. Write the integral that is used to find the volume.
about the x-axis. Write the integral that is used to find the volume.
A)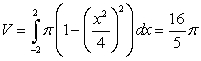
B)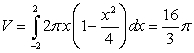
C)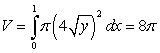
D)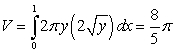
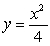 and
and 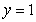 about the x-axis. Write the integral that is used to find the volume.
about the x-axis. Write the integral that is used to find the volume.A)
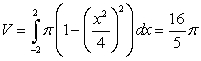
B)
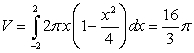
C)
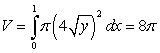
D)
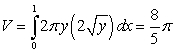

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
33
The base of a solid V is the region bounded by 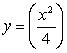 and
and 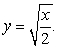 Find the volume if V has semicircular cross sections perpendicular to the x-axis.
Find the volume if V has semicircular cross sections perpendicular to the x-axis.
A)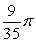
B)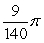
C)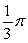
D)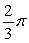
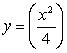 and
and 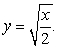 Find the volume if V has semicircular cross sections perpendicular to the x-axis.
Find the volume if V has semicircular cross sections perpendicular to the x-axis.A)
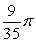
B)
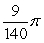
C)
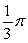
D)
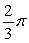

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
34
Let R be the region bounded by 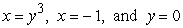 . Compute the volume of the solid formed by revolving R about x = 2.
. Compute the volume of the solid formed by revolving R about x = 2.
A)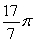
B)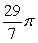
C)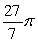

D)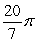
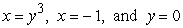 . Compute the volume of the solid formed by revolving R about x = 2.
. Compute the volume of the solid formed by revolving R about x = 2.A)
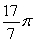
B)
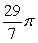
C)
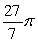

D)
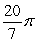

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
35
Sketch the solid bounded by 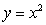 and the x-axis on the interval
and the x-axis on the interval 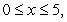 revolved about the line
revolved about the line 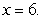 Draw a typical shell and write an integral that can be used to compute the volume of the solid.
Draw a typical shell and write an integral that can be used to compute the volume of the solid.
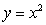 and the x-axis on the interval
and the x-axis on the interval 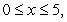 revolved about the line
revolved about the line 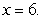 Draw a typical shell and write an integral that can be used to compute the volume of the solid.
Draw a typical shell and write an integral that can be used to compute the volume of the solid.
Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
36
Use cylindrical shells to compute the volume of the solid formed by revolving the region bounded by 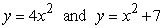 about x = 7.
about x = 7.
A)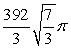
B)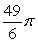
C)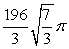
D)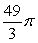
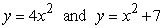 about x = 7.
about x = 7.A)
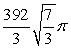
B)
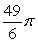
C)
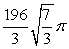
D)
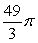

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
37
A solid is formed by revolving the given region about the given line. Round to three decimal places. Region bounded by y = sec x, y = 0, x = 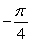 , and x =
, and x = 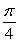 about y = -6
about y = -6
A) 72.737
B) 23.153
C) 250.39
D) 19.348
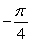 , and x =
, and x = 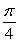 about y = -6
about y = -6A) 72.737
B) 23.153
C) 250.39
D) 19.348

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
38
Let R be the region bounded by 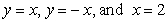 . Compute the volume of the solid formed by revolving R about y = 20.
. Compute the volume of the solid formed by revolving R about y = 20.
A)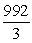
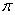
B)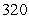
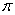
C)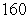
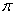
D)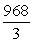
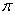
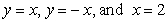 . Compute the volume of the solid formed by revolving R about y = 20.
. Compute the volume of the solid formed by revolving R about y = 20.A)
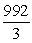
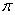
B)
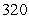
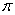
C)
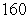
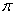
D)
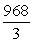

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
39
Use the best method available to find the volume of the solid formed by revolving the region bounded by 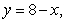
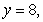 and
and 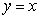 about the y-axis. Write the integral that is used to find the volume.
about the y-axis. Write the integral that is used to find the volume.
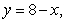
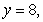 and
and 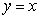 about the y-axis. Write the integral that is used to find the volume.
about the y-axis. Write the integral that is used to find the volume.
Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
40
Find the volume of the solid formed by revolving the region bounded by 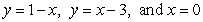 about x = 5.
about x = 5.
A)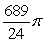
B)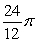
C)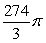
D)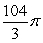
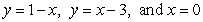 about x = 5.
about x = 5.A)
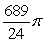
B)
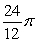
C)
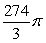
D)
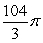

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
41
Set up the integral for the surface area of the surface of revolution and approximate the integral with a numerical method. Round answers to two decimal places. 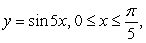 revolved about the x-axis
revolved about the x-axis
A)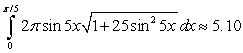
B)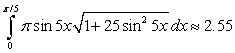
C)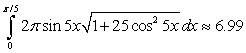
D)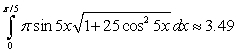
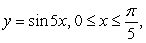 revolved about the x-axis
revolved about the x-axisA)
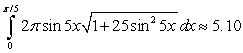
B)
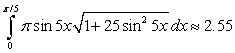
C)
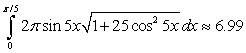
D)
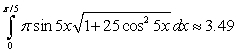

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
42
Identify the integral used to determine the surface area of the surface of revolution for the shape described by 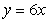 ,
, 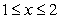 , revolved about the x-axis.
, revolved about the x-axis.
A)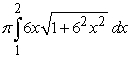
B)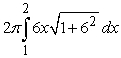
C)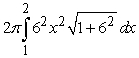
D)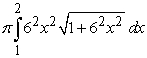
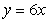 ,
, 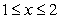 , revolved about the x-axis.
, revolved about the x-axis.A)
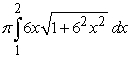
B)
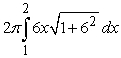
C)
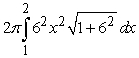
D)
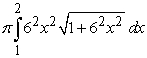

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
43
A person 6' tall wants to buy a jump rope. If , when the rope is at its lowest point, his hands will be 2' apart and 3' above the ground, and if the rope will take on the shape of a parabola just barely hitting the ground, how long must the rope be? [Consider the form of the rope to be described by the equation ![<strong>A person 6' tall wants to buy a jump rope. If , when the rope is at its lowest point, his hands will be 2' apart and 3' above the ground, and if the rope will take on the shape of a parabola just barely hitting the ground, how long must the rope be? [Consider the form of the rope to be described by the equation , with the origin being a spot on the ground underneath the jumper.]</strong> A) 6.75 feet B) 6.50 feet C) 6.25 feet D) 6.00 feet](https://storage.examlex.com/TB5869/11eaa88b_9194_5787_a696_75f89ab564b4_TB5869_11.jpg) , with the origin being a spot on the ground underneath the jumper.]
, with the origin being a spot on the ground underneath the jumper.]
A) 6.75 feet
B) 6.50 feet
C) 6.25 feet
D) 6.00 feet
![<strong>A person 6' tall wants to buy a jump rope. If , when the rope is at its lowest point, his hands will be 2' apart and 3' above the ground, and if the rope will take on the shape of a parabola just barely hitting the ground, how long must the rope be? [Consider the form of the rope to be described by the equation , with the origin being a spot on the ground underneath the jumper.]</strong> A) 6.75 feet B) 6.50 feet C) 6.25 feet D) 6.00 feet](https://storage.examlex.com/TB5869/11eaa88b_9194_5787_a696_75f89ab564b4_TB5869_11.jpg) , with the origin being a spot on the ground underneath the jumper.]
, with the origin being a spot on the ground underneath the jumper.]A) 6.75 feet
B) 6.50 feet
C) 6.25 feet
D) 6.00 feet

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
44
In a movie stunt, a car is driven off a cliff and falls into the ocean 200 feet below. If the car is going 50 feet/second (horizontally) when it goes over the cliff, its horizontal position is described as x = 50 t, where t is the time in seconds. Its vertical position is described as y = 16 t2, where y is the distance below the cliff (i.e. y = 200 when the car hits the ocean). Compute the length of the path traversed by the falling car. Round to the nearest foot. [Hint: The two equations will need to be combined, eliminating t so that y is expressed as a function of x.]
A) 274 feet
B) 279 feet
C) 284 feet
D) 289 feet
A) 274 feet
B) 279 feet
C) 284 feet
D) 289 feet

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
45
Identify the region (solid lines) and axis of revolution (dashed line) for the solid whose volume is described by the integral 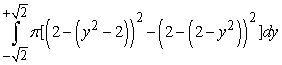 .
.
A)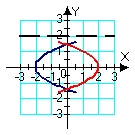
B)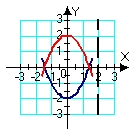
C)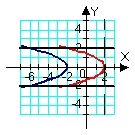
D)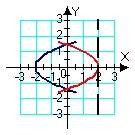
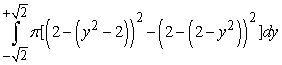 .
.A)

B)

C)

D)


Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
46
Two divers, one on the 15 ft platform and one on the 30 ft platform, hope to perform a joint dive in which they enter the water at the same time. If each begins with an upward jump with an initial velocity of at 14 ft/s, how much time difference should there be between the start of the two dives?
A) 0.43 s
B) 30.00 s
C) 0.38 s
D) 0.75 s
A) 0.43 s
B) 30.00 s
C) 0.38 s
D) 0.75 s

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
47
A solid shape described as the region bounded by 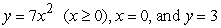 revolved around the y-axis, needs to have 1/4 of its volume trimmed off to meet a weight restriction. This will be done by reducing the radius of the piece - in other words, the resulting shape will be described as above, but with the region also bounded by x = q. Find the resulting radius, q.
revolved around the y-axis, needs to have 1/4 of its volume trimmed off to meet a weight restriction. This will be done by reducing the radius of the piece - in other words, the resulting shape will be described as above, but with the region also bounded by x = q. Find the resulting radius, q.
A)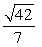
B)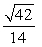
C)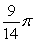
D)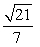
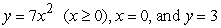 revolved around the y-axis, needs to have 1/4 of its volume trimmed off to meet a weight restriction. This will be done by reducing the radius of the piece - in other words, the resulting shape will be described as above, but with the region also bounded by x = q. Find the resulting radius, q.
revolved around the y-axis, needs to have 1/4 of its volume trimmed off to meet a weight restriction. This will be done by reducing the radius of the piece - in other words, the resulting shape will be described as above, but with the region also bounded by x = q. Find the resulting radius, q.A)
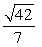
B)
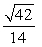
C)
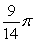
D)
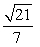

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
48
Compute the arc length exactly. 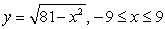
A)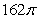
B)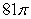
C)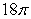
D)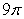
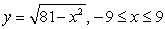
A)
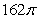
B)
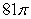
C)
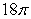
D)
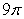

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
49
Identify the initial conditions y(0) and y'(0) for the vertical motion of an object , if the object thrown downward at a velocity of 6 feet per second from a height of 30 feet. [Take the origin to be on the ground.]
A) y(0) = 30, y'(0) = -6
B) y(0) = 0, y'(0) = -6
C) y(0) = 30, y'(0) = 6
D) y(0) = 0, y'(0) = 6
A) y(0) = 30, y'(0) = -6
B) y(0) = 0, y'(0) = -6
C) y(0) = 30, y'(0) = 6
D) y(0) = 0, y'(0) = 6

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
50
Set up the integral for arc length and then approximate the integral with a numerical method. Round answers to four decimal places. 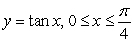
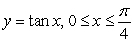

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
51
A 0.5 kg rock is dropped from the edge of a 52-foot cliff. How fast will it be going when it hits the ground at the base of the cliff?
A)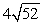 ft/s
ft/s
B)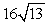 ft/s
ft/s
C) 52 ft/s
D)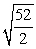 ft/s
ft/s
A)
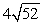 ft/s
ft/sB)
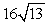 ft/s
ft/sC) 52 ft/s
D)
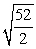 ft/s
ft/s
Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
52
Approximate the length of the curve using 4 secant lines. Round to three decimal places. y = x4 0 x 2
A) 32.301
B) 7.060
C) 16.608
D) 14.119
A) 32.301
B) 7.060
C) 16.608
D) 14.119

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
53
Pick the integral that represents a volume calculation by cylindrical shells that is equivalent to the following integral that represents a calculation of the same volume but by the method of washers. 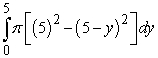
A)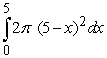
B)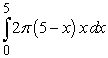
C)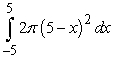
D)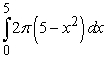
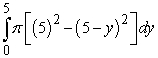
A)
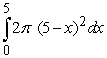
B)
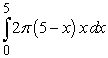
C)
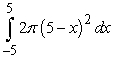
D)
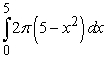

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
54
Compute the arc length exactly. 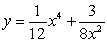 , -2 x -1
, -2 x -1
A)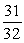
B)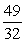
C)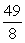
D)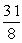
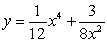 , -2 x -1
, -2 x -1A)
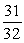
B)
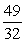
C)
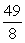
D)
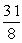

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
55
Identify the integral used to determine the surface area of the surface of revolution for the shape described by 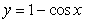 ,
, 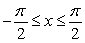 , revolved about the x-axis.
, revolved about the x-axis.
A)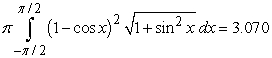
B)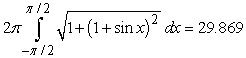
C)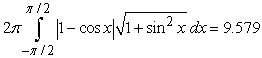
D)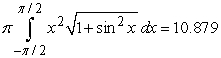
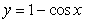 ,
, 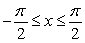 , revolved about the x-axis.
, revolved about the x-axis.A)
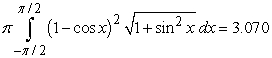
B)
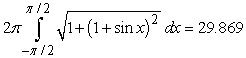
C)
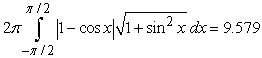
D)
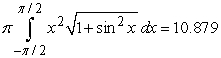

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
56
Molding is typically long, thin, decorative pieces of wood used, for instance, around windows or doors. The cross-section of a particular type of molding can be described as the region bounded by 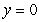 , x = 4, x = 0, and
, x = 4, x = 0, and 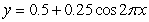 (all measured in inches), projected perpendicular to the xy-plane (see figure). If the manufacturer paints all four sides (but not the ends) and each gallon of paint covers 250 ft2, how many linear feet of molding can be coated with one gallon?
(all measured in inches), projected perpendicular to the xy-plane (see figure). If the manufacturer paints all four sides (but not the ends) and each gallon of paint covers 250 ft2, how many linear feet of molding can be coated with one gallon? 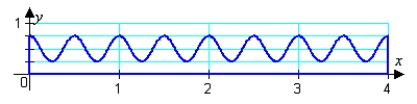
A) 315.8 feet
B) 264.2 feet
C) 512.4 feet
D) 128.1 feet
 , x = 4, x = 0, and
, x = 4, x = 0, and 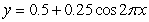 (all measured in inches), projected perpendicular to the xy-plane (see figure). If the manufacturer paints all four sides (but not the ends) and each gallon of paint covers 250 ft2, how many linear feet of molding can be coated with one gallon?
(all measured in inches), projected perpendicular to the xy-plane (see figure). If the manufacturer paints all four sides (but not the ends) and each gallon of paint covers 250 ft2, how many linear feet of molding can be coated with one gallon? 
A) 315.8 feet
B) 264.2 feet
C) 512.4 feet
D) 128.1 feet

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
57
Identify the initial conditions y(0) and y'(0) for the vertical motion of an object, if the object is dropped from a height of 45 feet. [Take the origin to be on the ground.]
A) y(0) = 0, y'(0) = 0
B) y(0) = 45, y'(0) = 45t
C) y(0) = 0, y'(0) = -45
D) y(0) = 45, y'(0) = 0
A) y(0) = 0, y'(0) = 0
B) y(0) = 45, y'(0) = 45t
C) y(0) = 0, y'(0) = -45
D) y(0) = 45, y'(0) = 0

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
58
Find the length of the curve defined by function 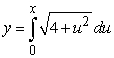 and extending from x = 0 to x = 4. Round your answer to three decimal places.
and extending from x = 0 to x = 4. Round your answer to three decimal places.
A) 12.228
B) 12.328
C) 12.428
D) 12.528
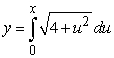 and extending from x = 0 to x = 4. Round your answer to three decimal places.
and extending from x = 0 to x = 4. Round your answer to three decimal places.A) 12.228
B) 12.328
C) 12.428
D) 12.528

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
59
An anthill is in the shape formed by revolving the region bounded by 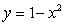 and the x-axis about the y-axis. A researcher removes a cylindrical core from the center of the hill. What should the radius be to give the researcher 5% of the dirt?
and the x-axis about the y-axis. A researcher removes a cylindrical core from the center of the hill. What should the radius be to give the researcher 5% of the dirt?
A) 0.8409
B) 0.6818
C) 0.1591
D) 0.3182
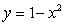 and the x-axis about the y-axis. A researcher removes a cylindrical core from the center of the hill. What should the radius be to give the researcher 5% of the dirt?
and the x-axis about the y-axis. A researcher removes a cylindrical core from the center of the hill. What should the radius be to give the researcher 5% of the dirt?A) 0.8409
B) 0.6818
C) 0.1591
D) 0.3182

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
60
Identify the region (solid lines) and axis of revolution (dashed line) for the solid whose volume is described by the integral 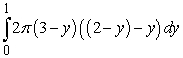 .
.
A)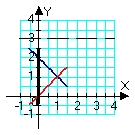
B)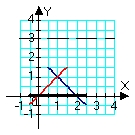
C)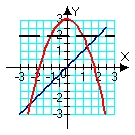
D)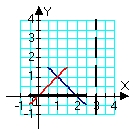
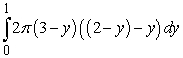 .
.A)

B)

C)

D)


Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
61
An object propelled from the ground with an initial velocity of 95 ft/s will reach a maximum height of 141.0 ft. If the initial velocity is increased 13%, by what percentage will the maximum height increase? Round percentages to the nearest integer.
A) 13%
B) 28%
C) 2%
D) 22%
A) 13%
B) 28%
C) 2%
D) 22%

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
62
A crash test is performed on a vehicle. The force of the wall on the front bumper is shown in the table. Estimate the impulse and the speed of the vehicle to the nearest whole number (use m = 200 slugs). 
A) impulse: 246,000 velocity: 1230 ft/s
B) impulse: 8200 velocity: 41 ft/s
C) impulse: 10,800 velocity: 54 ft/s
D) impulse: 324,000 velocity: 1620 ft/s

A) impulse: 246,000 velocity: 1230 ft/s
B) impulse: 8200 velocity: 41 ft/s
C) impulse: 10,800 velocity: 54 ft/s
D) impulse: 324,000 velocity: 1620 ft/s

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
63
A baseball pitcher releases the ball horizontally from a height of 5 ft with an initial speed of 120 ft/s. Find the height of the ball when it reaches home plate 60 feet away. Round to two decimal places. (Hint: Determine the time of flight from the x-equation, then use the y-equation to determine the height.)
A) 2.00 ft
B) 1.00 ft
C) 4.00 ft
D) 3.00 ft
A) 2.00 ft
B) 1.00 ft
C) 4.00 ft
D) 3.00 ft

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
64
A force of 7 pounds stretches a spring 7 inches. Find the work done in stretching this spring 10 inches beyond its natural length.
A)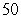 foot-pounds
foot-pounds
B)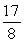 foot-pounds
foot-pounds
C)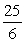 foot-pounds
foot-pounds
D)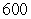 foot-pounds
foot-pounds
A)
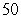 foot-pounds
foot-poundsB)
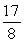 foot-pounds
foot-poundsC)
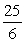 foot-pounds
foot-poundsD)
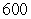 foot-pounds
foot-pounds
Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
65
A projectile passes overhead, and you attempt to shoot it down with a cannon. When it passes overhead it is traveling horizontally at 100 m/s at an elevation of 1000 m. Your cannon launches shells at 200 m/s, and in this instance you fire just as the projectile passes overhead and at an angle of 60o. In this scenario the horizontal velocities of the two projectiles are the same. At what elevation will the cannon shell and the other projectile collide?
A) They won't collide before the cannon shell hits the ground.
B) 971.7 m
C) 877.5 m
D) 836.7 m
A) They won't collide before the cannon shell hits the ground.
B) 971.7 m
C) 877.5 m
D) 836.7 m

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
66
A certain not-so-wiley coyote discovers that he just stepped off the edge of a cliff. Fourteen seconds later he hits the ground in a puff of dust. How high in meters is the cliff?
A) 1920.8 m
B) 960.4 m
C) 68.6 m
D) 137.2 m
A) 1920.8 m
B) 960.4 m
C) 68.6 m
D) 137.2 m

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
67
Where is the center of mass of a region of uniform density bounded by 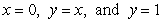 ?
?
A)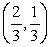
B)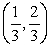
C)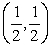
D)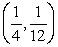
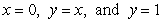 ?
?A)
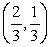
B)
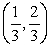
C)
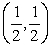
D)
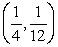

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
68
When pumping water out of a full hemispherical basin with radius r feet, how far down will the water level be when 1/4 of the work has been done? [The density of water is 62.4 lbs/ft3.]
A)![<strong>When pumping water out of a full hemispherical basin with radius r feet, how far down will the water level be when 1/4 of the work has been done? [The density of water is 62.4 lbs/ft<sup>3</sup>.]</strong> A) B) C) D)](https://storage.examlex.com/TB5869/11eaa88b_9199_d5ef_a696_5922a0b98813_TB5869_11.jpg)
B)![<strong>When pumping water out of a full hemispherical basin with radius r feet, how far down will the water level be when 1/4 of the work has been done? [The density of water is 62.4 lbs/ft<sup>3</sup>.]</strong> A) B) C) D)](https://storage.examlex.com/TB5869/11eaa88b_9199_fd00_a696_bf33ae795efb_TB5869_11.jpg)
C)![<strong>When pumping water out of a full hemispherical basin with radius r feet, how far down will the water level be when 1/4 of the work has been done? [The density of water is 62.4 lbs/ft<sup>3</sup>.]</strong> A) B) C) D)](https://storage.examlex.com/TB5869/11eaa88b_9199_fd01_a696_9fec50b5fdbd_TB5869_11.jpg)
D)![<strong>When pumping water out of a full hemispherical basin with radius r feet, how far down will the water level be when 1/4 of the work has been done? [The density of water is 62.4 lbs/ft<sup>3</sup>.]</strong> A) B) C) D)](https://storage.examlex.com/TB5869/11eaa88b_919a_2412_a696_73520bc80faf_TB5869_11.jpg)
A)
![<strong>When pumping water out of a full hemispherical basin with radius r feet, how far down will the water level be when 1/4 of the work has been done? [The density of water is 62.4 lbs/ft<sup>3</sup>.]</strong> A) B) C) D)](https://storage.examlex.com/TB5869/11eaa88b_9199_d5ef_a696_5922a0b98813_TB5869_11.jpg)
B)
![<strong>When pumping water out of a full hemispherical basin with radius r feet, how far down will the water level be when 1/4 of the work has been done? [The density of water is 62.4 lbs/ft<sup>3</sup>.]</strong> A) B) C) D)](https://storage.examlex.com/TB5869/11eaa88b_9199_fd00_a696_bf33ae795efb_TB5869_11.jpg)
C)
![<strong>When pumping water out of a full hemispherical basin with radius r feet, how far down will the water level be when 1/4 of the work has been done? [The density of water is 62.4 lbs/ft<sup>3</sup>.]</strong> A) B) C) D)](https://storage.examlex.com/TB5869/11eaa88b_9199_fd01_a696_9fec50b5fdbd_TB5869_11.jpg)
D)
![<strong>When pumping water out of a full hemispherical basin with radius r feet, how far down will the water level be when 1/4 of the work has been done? [The density of water is 62.4 lbs/ft<sup>3</sup>.]</strong> A) B) C) D)](https://storage.examlex.com/TB5869/11eaa88b_919a_2412_a696_73520bc80faf_TB5869_11.jpg)

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
69
A ball is thrown at an angle of ![<strong>A ball is thrown at an angle of with an initial speed of 25 meters/second. What is its time of flight ? [Assume the ball is thrown from ground level and lands at ground level.]</strong> A) 0.14 seconds B) 3.13 seconds C) 1.10 seconds D) 3.61 seconds](https://storage.examlex.com/TB5869/11eaa88b_9197_da11_a696_f3de59bbb9cc_TB5869_11.jpg) with an initial speed of 25 meters/second. What is its time of flight ? [Assume the ball is thrown from ground level and lands at ground level.]
with an initial speed of 25 meters/second. What is its time of flight ? [Assume the ball is thrown from ground level and lands at ground level.]
A) 0.14 seconds
B) 3.13 seconds
C) 1.10 seconds
D) 3.61 seconds
![<strong>A ball is thrown at an angle of with an initial speed of 25 meters/second. What is its time of flight ? [Assume the ball is thrown from ground level and lands at ground level.]</strong> A) 0.14 seconds B) 3.13 seconds C) 1.10 seconds D) 3.61 seconds](https://storage.examlex.com/TB5869/11eaa88b_9197_da11_a696_f3de59bbb9cc_TB5869_11.jpg) with an initial speed of 25 meters/second. What is its time of flight ? [Assume the ball is thrown from ground level and lands at ground level.]
with an initial speed of 25 meters/second. What is its time of flight ? [Assume the ball is thrown from ground level and lands at ground level.]A) 0.14 seconds
B) 3.13 seconds
C) 1.10 seconds
D) 3.61 seconds

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
70
An object is dropped from a height of 140 feet. Another object directly below the first is launched vertically from the ground with an initial velocity of 70 ft/s. Determine when and how high up the objects collide.

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
71
Compute the weight in ounces of an object extending from x = -5 to x = 25 with density 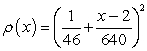 slugs/in. Round answer to nearest whole number.
slugs/in. Round answer to nearest whole number.
A) 21 oz
B) 4 oz
C) 86 oz
D) 443 oz
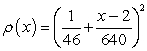 slugs/in. Round answer to nearest whole number.
slugs/in. Round answer to nearest whole number.A) 21 oz
B) 4 oz
C) 86 oz
D) 443 oz

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
72
A water tower is spherical in shape with radius 50 feet, extending from 100 to 200 feet above ground. Compute the work done in filling the tank from the ground.

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
73
A 30-foot chain weighs 750 pounds and is hauled up to the deck of a boat. The chain is oriented vertically and the top of the chain starts 30 feet below the deck. Compute the work done.
A) 11,250 foot-pounds
B) 22,875 foot-pounds
C) 375 foot-pounds
D) 33,750 foot-pounds
A) 11,250 foot-pounds
B) 22,875 foot-pounds
C) 375 foot-pounds
D) 33,750 foot-pounds

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
74
In a baseball game a base-runner can attempt to advance when a fielder catches a hit ball before it reaches the ground, so long as the runner doesn't leave base before the fielder catches the ball. The fielder then attempts to throw the ball to the base ahead of the runner. If a base-runner can run from 3rd base to home plate in 4.6 sec, how fast must the centerfielder's throw leave his hand if he makes the catch then immediately throws the ball 370 ft from home plate? Assume the base-runner leaves his base at the same instant the centerfielder throws the ball, and that the ball reaches the catcher standing over home plate at the same height from which it was thrown and at the same time the runner would reach the plate. [Hint: This is basically a problem of determining how much initial vertical velocity the ball needs to stay in the air long enough to reach the plate.]
A) 80 ft/sec
B) 74 ft/sec
C) 109 ft/sec
D) 154 ft/sec
A) 80 ft/sec
B) 74 ft/sec
C) 109 ft/sec
D) 154 ft/sec

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
75
When a certain spring is stretched 0.20 m, 7  of work is done. What is the spring's "spring constant"?
of work is done. What is the spring's "spring constant"?
A) 350.0 N/m
B) 175.0 N/m
C) 35.0 N/m
D) 17.5 N/m
 of work is done. What is the spring's "spring constant"?
of work is done. What is the spring's "spring constant"?A) 350.0 N/m
B) 175.0 N/m
C) 35.0 N/m
D) 17.5 N/m

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
76
A cylindrical water tank has a radius of 4 feet and a height of 3.0 feet. Compute the work done to pump the water out of a filled tank through the top. [The density of water is 62.4 lbs/ft3.]
A) 14,115 ft-lbs
B) 4705 ft-lbs
C) 281 ft-lbs
D) 7390 ft-lbs
A) 14,115 ft-lbs
B) 4705 ft-lbs
C) 281 ft-lbs
D) 7390 ft-lbs

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
77
What is the minimum speed a ball must be thrown upward if it is to reach a height of 13 feet?
A) 13 ft/s
B)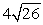 ft/s
ft/s
C)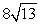 ft/s
ft/s
D) 0 ft/s
A) 13 ft/s
B)
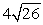 ft/s
ft/sC)
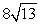 ft/s
ft/sD) 0 ft/s

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
78
A projectile traveling with momentum 4 kg m/s in one direction undergoes an impulse in the opposite direction. The force of the impulse is described as 6000(sin500t) kg m/s2 and it is exerted over a time range 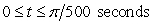 . What is the object's momentum (in the direction of the impulse) after the impulse?
. What is the object's momentum (in the direction of the impulse) after the impulse?
A) 8 kg m/s
B) -20 kg m/s
C) -19 kg m/s
D) 16 kg m/s
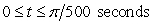 . What is the object's momentum (in the direction of the impulse) after the impulse?
. What is the object's momentum (in the direction of the impulse) after the impulse?A) 8 kg m/s
B) -20 kg m/s
C) -19 kg m/s
D) 16 kg m/s

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
79
Starting with the expression for work 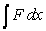 , one can change the look of the expression without changing what it represents by dividing the force F by the area it is applied over and multiplying the differential distance dx by that same area. Force divided by area is a pressure (P), and area times the differential distance is a differential volume. Hence one can also describe work as
, one can change the look of the expression without changing what it represents by dividing the force F by the area it is applied over and multiplying the differential distance dx by that same area. Force divided by area is a pressure (P), and area times the differential distance is a differential volume. Hence one can also describe work as 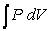 . A gas at constant temperature will change its pressure inversely to changes in volume,
. A gas at constant temperature will change its pressure inversely to changes in volume, 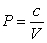 . If a sample of gas has a pressure of 1 atmosphere when its volume is 1 L, how much work does it do when it expands from 1 L to 3 L?
. If a sample of gas has a pressure of 1 atmosphere when its volume is 1 L, how much work does it do when it expands from 1 L to 3 L?
A)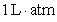
B)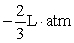
C)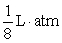
D)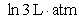
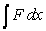 , one can change the look of the expression without changing what it represents by dividing the force F by the area it is applied over and multiplying the differential distance dx by that same area. Force divided by area is a pressure (P), and area times the differential distance is a differential volume. Hence one can also describe work as
, one can change the look of the expression without changing what it represents by dividing the force F by the area it is applied over and multiplying the differential distance dx by that same area. Force divided by area is a pressure (P), and area times the differential distance is a differential volume. Hence one can also describe work as 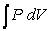 . A gas at constant temperature will change its pressure inversely to changes in volume,
. A gas at constant temperature will change its pressure inversely to changes in volume, 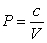 . If a sample of gas has a pressure of 1 atmosphere when its volume is 1 L, how much work does it do when it expands from 1 L to 3 L?
. If a sample of gas has a pressure of 1 atmosphere when its volume is 1 L, how much work does it do when it expands from 1 L to 3 L?A)
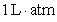
B)
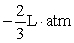
C)
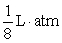
D)
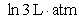

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
80
Identify the mass of a thin wire with density 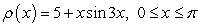 .
.
A)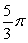
B)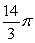
C)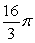
D)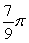
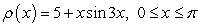 .
.A)
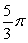
B)
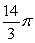
C)
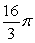
D)
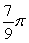

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck


