Deck 3: Differentiation
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/330
Play
Full screen (f)
Deck 3: Differentiation
1
Let f be the function defined by 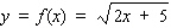 . Use the differential of f to find the approximate change in y if x changes from 4 to 4.1.
. Use the differential of f to find the approximate change in y if x changes from 4 to 4.1.
A) 0.02774
B) 0.36056
C) 1.10940
D) 0.05547
E) 0.01387
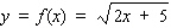 . Use the differential of f to find the approximate change in y if x changes from 4 to 4.1.
. Use the differential of f to find the approximate change in y if x changes from 4 to 4.1.A) 0.02774
B) 0.36056
C) 1.10940
D) 0.05547
E) 0.01387
0.02774
2
Find the differential of the function. 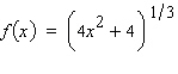
A)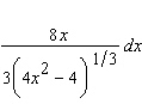
B)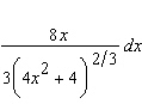
C)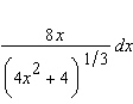
D)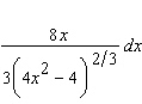
E)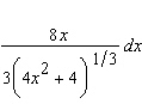
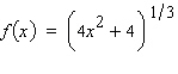
A)
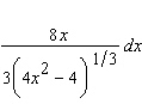
B)
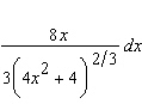
C)
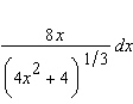
D)
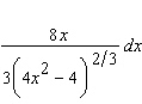
E)
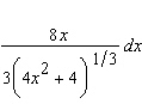
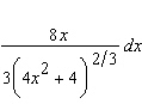
3
Use a differential to approximate 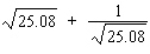 . Hint: Let
. Hint: Let 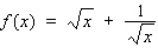 and compute dy with x = 25 and dx = 0.08 .
and compute dy with x = 25 and dx = 0.08 .
A) 5.14381
B) 6.18124
C) 5.38115
D) 5.20768
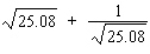 . Hint: Let
. Hint: Let 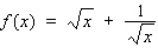 and compute dy with x = 25 and dx = 0.08 .
and compute dy with x = 25 and dx = 0.08 .A) 5.14381
B) 6.18124
C) 5.38115
D) 5.20768
5.20768
4
Find the differential of the function. 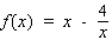
A)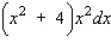
B)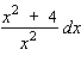
C)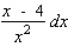
D)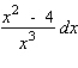
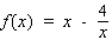
A)
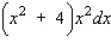
B)
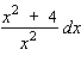
C)
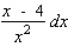
D)
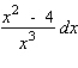

Unlock Deck
Unlock for access to all 330 flashcards in this deck.
Unlock Deck
k this deck
5
Use a differential to approximate the quantity to the nearest thousandth. 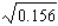
A)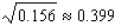
B)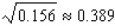
C)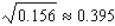
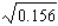
A)
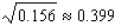
B)
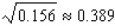
C)
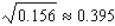

Unlock Deck
Unlock for access to all 330 flashcards in this deck.
Unlock Deck
k this deck
6
Lupe deposits a sum of $5,000 into an account that pays interest at the rate of r/year compounded monthly. Her investment at the end of 10 yr is given by 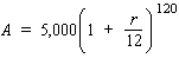 . Approximately how much more would Lupe's account be worth at the end of the term if her account paid 9.1%/year instead of 9%/year? 9.2%/year instead of 9%/year? 9.3%/year instead of 9%/year?
. Approximately how much more would Lupe's account be worth at the end of the term if her account paid 9.1%/year instead of 9%/year? 9.2%/year instead of 9%/year? 9.3%/year instead of 9%/year?
(Hint: Use the differential of A to answer this questions.)
A) $122.66, $243.31, $367.97
B) $121.66, $263.31, $364.97
C) $111.66, $263.31, $394.97
D) $122.66, $241.31, $367.97
E) $121.66, $243.31, $364.97
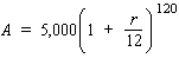 . Approximately how much more would Lupe's account be worth at the end of the term if her account paid 9.1%/year instead of 9%/year? 9.2%/year instead of 9%/year? 9.3%/year instead of 9%/year?
. Approximately how much more would Lupe's account be worth at the end of the term if her account paid 9.1%/year instead of 9%/year? 9.2%/year instead of 9%/year? 9.3%/year instead of 9%/year?(Hint: Use the differential of A to answer this questions.)
A) $122.66, $243.31, $367.97
B) $121.66, $263.31, $364.97
C) $111.66, $263.31, $394.97
D) $122.66, $241.31, $367.97
E) $121.66, $243.31, $364.97

Unlock Deck
Unlock for access to all 330 flashcards in this deck.
Unlock Deck
k this deck
7
Let f be the function defined by 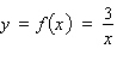 . Find the approximate change in y if x changes from
. Find the approximate change in y if x changes from 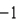 to
to 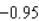 . Find the actual change in y if x changes from
. Find the actual change in y if x changes from 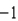 to
to 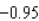 .
.
A)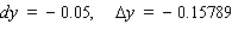
B)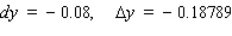
C)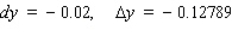
D)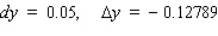
E)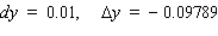
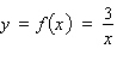 . Find the approximate change in y if x changes from
. Find the approximate change in y if x changes from 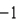 to
to 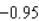 . Find the actual change in y if x changes from
. Find the actual change in y if x changes from 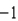 to
to 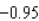 .
.A)
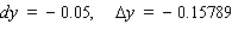
B)
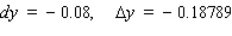
C)
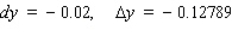
D)
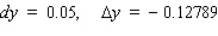
E)
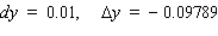

Unlock Deck
Unlock for access to all 330 flashcards in this deck.
Unlock Deck
k this deck
8
Find the differential of the function. 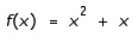
A)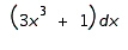
B)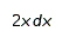
C)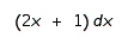
D)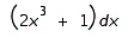
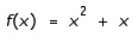
A)
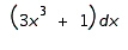
B)
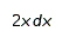
C)
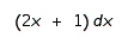
D)
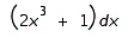

Unlock Deck
Unlock for access to all 330 flashcards in this deck.
Unlock Deck
k this deck
9
Find the differential of the function. 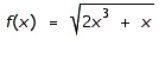
A)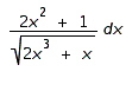
B)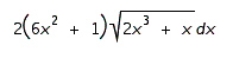
C)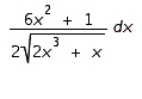
D)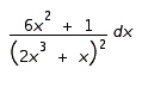
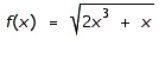
A)
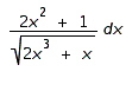
B)
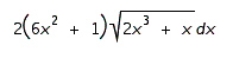
C)
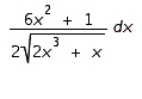
D)
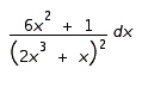

Unlock Deck
Unlock for access to all 330 flashcards in this deck.
Unlock Deck
k this deck
10
Use a differential to approximate the quantity to the nearest thousandth. 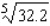
A)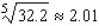
B)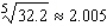
C)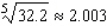
D)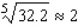
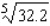
A)
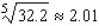
B)
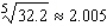
C)
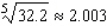
D)
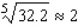

Unlock Deck
Unlock for access to all 330 flashcards in this deck.
Unlock Deck
k this deck
11
Find the differential of the function. 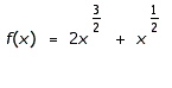
A)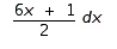
B)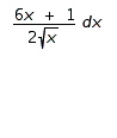
C)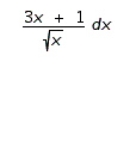
D)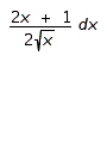
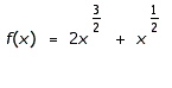
A)
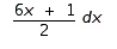
B)
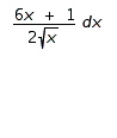
C)
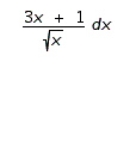
D)
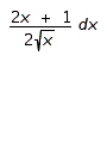

Unlock Deck
Unlock for access to all 330 flashcards in this deck.
Unlock Deck
k this deck
12
Let f be the function defined by 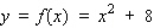 . Find the approximate change in y if x changes from 1 to 1.08. Find the actual change in y if x changes from 1 to 1.08.
. Find the approximate change in y if x changes from 1 to 1.08. Find the actual change in y if x changes from 1 to 1.08.
A)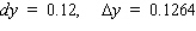
B)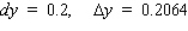
C)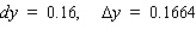
D)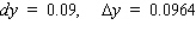
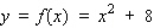 . Find the approximate change in y if x changes from 1 to 1.08. Find the actual change in y if x changes from 1 to 1.08.
. Find the approximate change in y if x changes from 1 to 1.08. Find the actual change in y if x changes from 1 to 1.08.A)
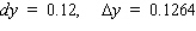
B)
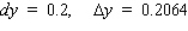
C)
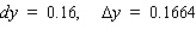
D)
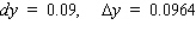

Unlock Deck
Unlock for access to all 330 flashcards in this deck.
Unlock Deck
k this deck
13
The supply equation for a certain brand of radio is given by 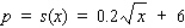 , where x is the quantity supplied and p is the unit price in dollars. Use differentials to approximate the change in price when the quantity supplied is increased from 10,000 units to 10,500 units.
, where x is the quantity supplied and p is the unit price in dollars. Use differentials to approximate the change in price when the quantity supplied is increased from 10,000 units to 10,500 units.
A) $0.75
B) $7.00
C) $1.00
D) $0.50
E) $6.50
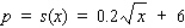 , where x is the quantity supplied and p is the unit price in dollars. Use differentials to approximate the change in price when the quantity supplied is increased from 10,000 units to 10,500 units.
, where x is the quantity supplied and p is the unit price in dollars. Use differentials to approximate the change in price when the quantity supplied is increased from 10,000 units to 10,500 units.A) $0.75
B) $7.00
C) $1.00
D) $0.50
E) $6.50

Unlock Deck
Unlock for access to all 330 flashcards in this deck.
Unlock Deck
k this deck
14
Find the differential of the function. 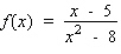
A)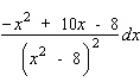
B)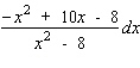
C)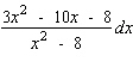
D)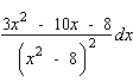
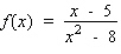
A)
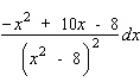
B)
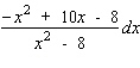
C)
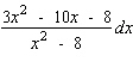
D)
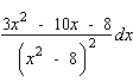

Unlock Deck
Unlock for access to all 330 flashcards in this deck.
Unlock Deck
k this deck
15
Find the differential of the function. 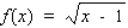
A)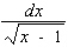
B)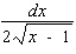
C)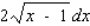
D)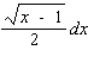
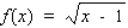
A)
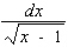
B)
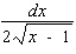
C)
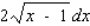
D)
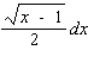

Unlock Deck
Unlock for access to all 330 flashcards in this deck.
Unlock Deck
k this deck
16
Find the differential of the function. 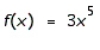
A)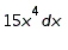
B)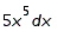
C)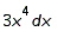
D)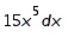
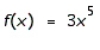
A)
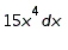
B)
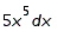
C)
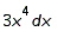
D)
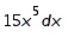

Unlock Deck
Unlock for access to all 330 flashcards in this deck.
Unlock Deck
k this deck
17
Use a differential to approximate the quantity to the nearest thousandth. 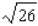
A)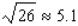
B)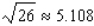
C)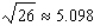
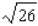
A)
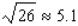
B)
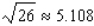
C)
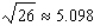

Unlock Deck
Unlock for access to all 330 flashcards in this deck.
Unlock Deck
k this deck
18
The volume of a spherical cancerous tumor is given by 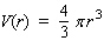 . If the radius of a tumor is estimated at 1.2 cm, with a maximum error in measurement of 0.004 cm, determine the error that might occur when the volume of the tumor is calculated.
. If the radius of a tumor is estimated at 1.2 cm, with a maximum error in measurement of 0.004 cm, determine the error that might occur when the volume of the tumor is calculated.
A)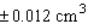
B)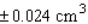
C)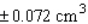
D)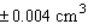
E)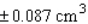
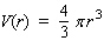 . If the radius of a tumor is estimated at 1.2 cm, with a maximum error in measurement of 0.004 cm, determine the error that might occur when the volume of the tumor is calculated.
. If the radius of a tumor is estimated at 1.2 cm, with a maximum error in measurement of 0.004 cm, determine the error that might occur when the volume of the tumor is calculated.A)
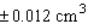
B)
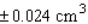
C)
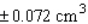
D)
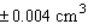
E)
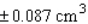

Unlock Deck
Unlock for access to all 330 flashcards in this deck.
Unlock Deck
k this deck
19
The supply equation for a certain brand of radio is given by 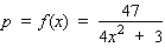 , where p is expressed in dollars/bushel and x, the quantity demanded each year, is measured in billions of bushels. The economists are forecasting a harvest of 1.8 billion bushels for the year, with a maximum error of 15% in their forecast. Determine the corresponding maximum error in the predicted price per bushel of soybeans. Round the answer to the nearest percent.
, where p is expressed in dollars/bushel and x, the quantity demanded each year, is measured in billions of bushels. The economists are forecasting a harvest of 1.8 billion bushels for the year, with a maximum error of 15% in their forecast. Determine the corresponding maximum error in the predicted price per bushel of soybeans. Round the answer to the nearest percent.
A)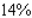
B)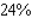
C)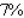
D)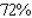
E)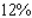
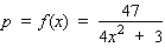 , where p is expressed in dollars/bushel and x, the quantity demanded each year, is measured in billions of bushels. The economists are forecasting a harvest of 1.8 billion bushels for the year, with a maximum error of 15% in their forecast. Determine the corresponding maximum error in the predicted price per bushel of soybeans. Round the answer to the nearest percent.
, where p is expressed in dollars/bushel and x, the quantity demanded each year, is measured in billions of bushels. The economists are forecasting a harvest of 1.8 billion bushels for the year, with a maximum error of 15% in their forecast. Determine the corresponding maximum error in the predicted price per bushel of soybeans. Round the answer to the nearest percent.A)
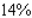
B)
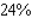
C)
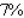
D)
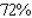
E)
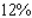

Unlock Deck
Unlock for access to all 330 flashcards in this deck.
Unlock Deck
k this deck
20
Find the differential of the function. 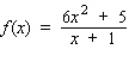
A)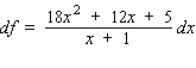
B)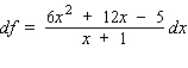
C)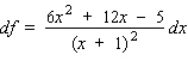
D)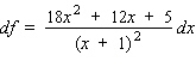
E)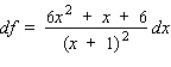
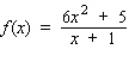
A)
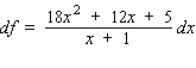
B)
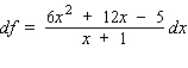
C)
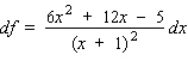
D)
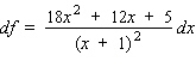
E)
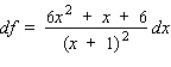

Unlock Deck
Unlock for access to all 330 flashcards in this deck.
Unlock Deck
k this deck
21
A study prepared for the National Association of Realtors estimates that the number of housing starts per year over the next 5 yr will be 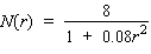 million units, where r (percent) is the mortgage rate. Use differentials to estimate the decrease in the number of housing starts when the mortgage rate is increased from 10% to 10.6%. Round to the nearest unit.
million units, where r (percent) is the mortgage rate. Use differentials to estimate the decrease in the number of housing starts when the mortgage rate is increased from 10% to 10.6%. Round to the nearest unit.
Give your answer as a number without the units.
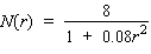 million units, where r (percent) is the mortgage rate. Use differentials to estimate the decrease in the number of housing starts when the mortgage rate is increased from 10% to 10.6%. Round to the nearest unit.
million units, where r (percent) is the mortgage rate. Use differentials to estimate the decrease in the number of housing starts when the mortgage rate is increased from 10% to 10.6%. Round to the nearest unit.Give your answer as a number without the units.

Unlock Deck
Unlock for access to all 330 flashcards in this deck.
Unlock Deck
k this deck
22
A study prepared for the National Association of Realtors estimates that the number of housing starts per year over the next 5 yr will be 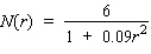 million units, where r (percent) is the mortgage rate. Use differentials to estimate the decrease in the number of housing starts when the mortgage rate is increased from 17% to 17.8%. Round to the nearest unit.
million units, where r (percent) is the mortgage rate. Use differentials to estimate the decrease in the number of housing starts when the mortgage rate is increased from 17% to 17.8%. Round to the nearest unit.
A) 20,119 housing starts
B) 20,133 housing starts
C) 20,856 housing starts
D) 19,172 housing starts
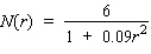 million units, where r (percent) is the mortgage rate. Use differentials to estimate the decrease in the number of housing starts when the mortgage rate is increased from 17% to 17.8%. Round to the nearest unit.
million units, where r (percent) is the mortgage rate. Use differentials to estimate the decrease in the number of housing starts when the mortgage rate is increased from 17% to 17.8%. Round to the nearest unit.A) 20,119 housing starts
B) 20,133 housing starts
C) 20,856 housing starts
D) 19,172 housing starts

Unlock Deck
Unlock for access to all 330 flashcards in this deck.
Unlock Deck
k this deck
23
A sociologist has found that the number of serious crimes in a certain city each year is described by the function 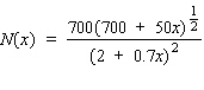 , where x (in cents/dollar deposited) is the level of reinvestment in the area in conventional mortgages by the city's ten largest banks. Use differentials to estimate the change in the number of crimes if the level of reinvestment changes from 16
, where x (in cents/dollar deposited) is the level of reinvestment in the area in conventional mortgages by the city's ten largest banks. Use differentials to estimate the change in the number of crimes if the level of reinvestment changes from 16 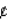 /dollar deposited to 25
/dollar deposited to 25 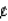 /dollar deposited. Round to the nearest integer.
/dollar deposited. Round to the nearest integer.
A) Decrease of 125 crimes/yr.
B) Decrease of 155 crimes/yr.
C) Decrease of 122 crimes/yr.
D) Decrease of 88 crimes/yr.
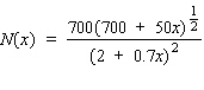 , where x (in cents/dollar deposited) is the level of reinvestment in the area in conventional mortgages by the city's ten largest banks. Use differentials to estimate the change in the number of crimes if the level of reinvestment changes from 16
, where x (in cents/dollar deposited) is the level of reinvestment in the area in conventional mortgages by the city's ten largest banks. Use differentials to estimate the change in the number of crimes if the level of reinvestment changes from 16 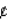 /dollar deposited to 25
/dollar deposited to 25 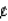 /dollar deposited. Round to the nearest integer.
/dollar deposited. Round to the nearest integer.A) Decrease of 125 crimes/yr.
B) Decrease of 155 crimes/yr.
C) Decrease of 122 crimes/yr.
D) Decrease of 88 crimes/yr.

Unlock Deck
Unlock for access to all 330 flashcards in this deck.
Unlock Deck
k this deck
24
Use a differential to approximate 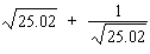 .
.
Round the result to five decimal places, if necessary.
Hint: Let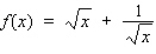 and compute dy with x = 25 and dx = 0.02 .
and compute dy with x = 25 and dx = 0.02 . 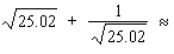 __________
__________
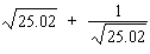 .
.Round the result to five decimal places, if necessary.
Hint: Let
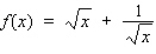 and compute dy with x = 25 and dx = 0.02 .
and compute dy with x = 25 and dx = 0.02 . 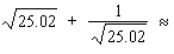 __________
__________
Unlock Deck
Unlock for access to all 330 flashcards in this deck.
Unlock Deck
k this deck
25
The supply equation for a certain brand of radio is given by 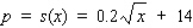 , where x is the quantity supplied and p is the unit price in dollars. Use differentials to approximate the change in price when the quantity supplied is increased from 10,000 units to 10,500 units.
, where x is the quantity supplied and p is the unit price in dollars. Use differentials to approximate the change in price when the quantity supplied is increased from 10,000 units to 10,500 units.
$__________
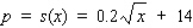 , where x is the quantity supplied and p is the unit price in dollars. Use differentials to approximate the change in price when the quantity supplied is increased from 10,000 units to 10,500 units.
, where x is the quantity supplied and p is the unit price in dollars. Use differentials to approximate the change in price when the quantity supplied is increased from 10,000 units to 10,500 units.$__________

Unlock Deck
Unlock for access to all 330 flashcards in this deck.
Unlock Deck
k this deck
26
Use a differential to approximate the quantity. 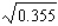 Round the result to the nearest thousandth, if necessary.
Round the result to the nearest thousandth, if necessary. 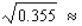 __________
__________
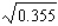 Round the result to the nearest thousandth, if necessary.
Round the result to the nearest thousandth, if necessary. 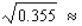 __________
__________
Unlock Deck
Unlock for access to all 330 flashcards in this deck.
Unlock Deck
k this deck
27
Use a differential to approximate the quantity. 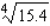 Round the result to the nearest thousandth, if necessary.
Round the result to the nearest thousandth, if necessary. 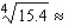 __________
__________
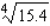 Round the result to the nearest thousandth, if necessary.
Round the result to the nearest thousandth, if necessary. 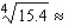 __________
__________
Unlock Deck
Unlock for access to all 330 flashcards in this deck.
Unlock Deck
k this deck
28
The length of time (in seconds) a certain individual takes to learn a list of n items is approximated by 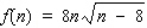 .
.
Use differentials to approximate the additional time it takes the individual to learn the items on a list when n is increased from 72 to 78 items. Round to the nearest second.
__________ sec
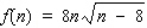 .
.Use differentials to approximate the additional time it takes the individual to learn the items on a list when n is increased from 72 to 78 items. Round to the nearest second.
__________ sec

Unlock Deck
Unlock for access to all 330 flashcards in this deck.
Unlock Deck
k this deck
29
Research done in the 1930s by the French physiologist Jean Poiseuille showed that the resistance R of a blood vessel of length l and radius r is 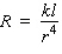 where k is a constant. Suppose a dose of the drug TPA increases r by 22%. How will this affect the resistance R? Assume that l is constant.
where k is a constant. Suppose a dose of the drug TPA increases r by 22%. How will this affect the resistance R? Assume that l is constant.
A) It will increase by 110%.
B) It will drop by 110%.
C) It will increase by 88%.
D) It will drop by 88%.
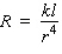 where k is a constant. Suppose a dose of the drug TPA increases r by 22%. How will this affect the resistance R? Assume that l is constant.
where k is a constant. Suppose a dose of the drug TPA increases r by 22%. How will this affect the resistance R? Assume that l is constant.A) It will increase by 110%.
B) It will drop by 110%.
C) It will increase by 88%.
D) It will drop by 88%.

Unlock Deck
Unlock for access to all 330 flashcards in this deck.
Unlock Deck
k this deck
30
The length of each edge of a cube is 18 cm, with a possible error in measurement of 0.01 cm. Use differentials to estimate the error that might occur when the volume of the cube is calculated.
Round the result to the nearest hundredth, if necessary.
An error is approximately __________
__________ 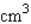 .
.
Round the result to the nearest hundredth, if necessary.
An error is approximately
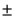 __________
__________ 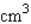 .
.
Unlock Deck
Unlock for access to all 330 flashcards in this deck.
Unlock Deck
k this deck
31
The length of each edge of a cube is 19 cm, with a possible error in measurement of 0.01 cm. Use differentials to estimate the error that might occur when the volume of the cube is calculated.
A) An error is approximately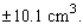
B) An error is approximately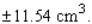
C) An error is approximately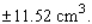
D) An error is approximately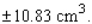
A) An error is approximately
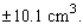
B) An error is approximately
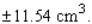
C) An error is approximately
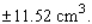
D) An error is approximately
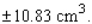

Unlock Deck
Unlock for access to all 330 flashcards in this deck.
Unlock Deck
k this deck
32
Research done in the 1930s by the French physiologist Jean Poiseuille showed that the resistance R of a blood vessel of length l and radius r is 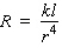 , where k is a constant. Suppose a dose of the drug TPA increases r by 14%. How will this affect the resistance R? Assume that l is constant.
, where k is a constant. Suppose a dose of the drug TPA increases r by 14%. How will this affect the resistance R? Assume that l is constant.
It will drop by __________%.
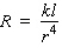 , where k is a constant. Suppose a dose of the drug TPA increases r by 14%. How will this affect the resistance R? Assume that l is constant.
, where k is a constant. Suppose a dose of the drug TPA increases r by 14%. How will this affect the resistance R? Assume that l is constant.It will drop by __________%.

Unlock Deck
Unlock for access to all 330 flashcards in this deck.
Unlock Deck
k this deck
33
A hemisphere-shaped dome of radius 40 ft is to be coated with a layer of rust-proofer before painting. Use differentials to estimate the amount of rust-proofer needed if the coat is to be 0.01 in. thick.
Round the result to the nearest hundredth, if necessary.
Hint: The volume of a hemisphere of radius r is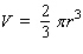 .
.
__________
Round the result to the nearest hundredth, if necessary.
Hint: The volume of a hemisphere of radius r is
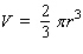 .
.__________
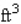

Unlock Deck
Unlock for access to all 330 flashcards in this deck.
Unlock Deck
k this deck
34
A hemisphere-shaped dome of radius 30 ft is to be coated with a layer of rust-proofer before painting. Use differentials to estimate the amount of rust-proofer needed if the coat is to be 0.05 in. thick. Hint: The volume of a hemisphere of radius r is 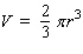 .
.
A)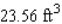
B)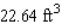
C)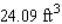
D)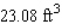
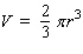 .
.A)
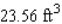
B)
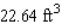
C)
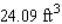
D)
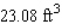

Unlock Deck
Unlock for access to all 330 flashcards in this deck.
Unlock Deck
k this deck
35
A sociologist has found that the number of serious crimes in a certain city each year is described by the function 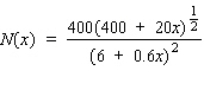 where x (in cents/dollar deposited) is the level of reinvestment in the area in conventional mortgages by the city's ten largest banks. Use differentials to estimate the change in the number of crimes if the level of reinvestment changes from 27
where x (in cents/dollar deposited) is the level of reinvestment in the area in conventional mortgages by the city's ten largest banks. Use differentials to estimate the change in the number of crimes if the level of reinvestment changes from 27 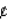 /dollar deposited to 34
/dollar deposited to 34 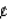 /dollar deposited. Round to the nearest integer.
/dollar deposited. Round to the nearest integer.
Decrease of __________ crimes/yr.
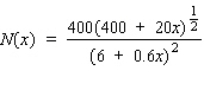 where x (in cents/dollar deposited) is the level of reinvestment in the area in conventional mortgages by the city's ten largest banks. Use differentials to estimate the change in the number of crimes if the level of reinvestment changes from 27
where x (in cents/dollar deposited) is the level of reinvestment in the area in conventional mortgages by the city's ten largest banks. Use differentials to estimate the change in the number of crimes if the level of reinvestment changes from 27 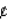 /dollar deposited to 34
/dollar deposited to 34  /dollar deposited. Round to the nearest integer.
/dollar deposited. Round to the nearest integer.Decrease of __________ crimes/yr.

Unlock Deck
Unlock for access to all 330 flashcards in this deck.
Unlock Deck
k this deck
36
The length of time (in seconds) a certain individual takes to learn a list of n items is approximated by 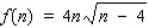 . Use differentials to approximate the additional time it takes the individual to learn the items on a list when n is increased from 68 to 76 items. Round to the nearest second.
. Use differentials to approximate the additional time it takes the individual to learn the items on a list when n is increased from 68 to 76 items. Round to the nearest second.
A) 348 sec
B) 385 sec
C) 436 sec
D) 392 sec
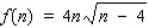 . Use differentials to approximate the additional time it takes the individual to learn the items on a list when n is increased from 68 to 76 items. Round to the nearest second.
. Use differentials to approximate the additional time it takes the individual to learn the items on a list when n is increased from 68 to 76 items. Round to the nearest second.A) 348 sec
B) 385 sec
C) 436 sec
D) 392 sec

Unlock Deck
Unlock for access to all 330 flashcards in this deck.
Unlock Deck
k this deck
37
The volume of a spherical cancerous tumor is given by 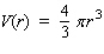 .
.
If the radius of a tumor is estimated at 0.7 cm, with a maximum error in measurement of 0.007 cm, determine the error that might occur when the volume of the tumor is calculated. Round the answer to the nearest thousandth, if necessary.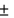 __________
__________ 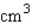
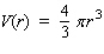 .
.If the radius of a tumor is estimated at 0.7 cm, with a maximum error in measurement of 0.007 cm, determine the error that might occur when the volume of the tumor is calculated. Round the answer to the nearest thousandth, if necessary.
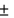 __________
__________ 

Unlock Deck
Unlock for access to all 330 flashcards in this deck.
Unlock Deck
k this deck
38
Use a differential to approximate the quantity. 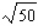 Round the result to the nearest thousandth, if necessary.
Round the result to the nearest thousandth, if necessary. 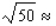 __________
__________
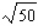 Round the result to the nearest thousandth, if necessary.
Round the result to the nearest thousandth, if necessary. 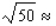 __________
__________
Unlock Deck
Unlock for access to all 330 flashcards in this deck.
Unlock Deck
k this deck
39
Use a differential to approximate the quantity to the nearest thousandth. 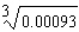
A)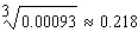
B)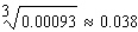
C)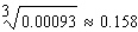
D)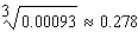
E)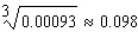
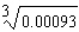
A)
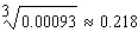
B)
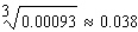
C)
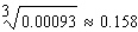
D)
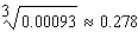
E)
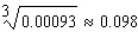

Unlock Deck
Unlock for access to all 330 flashcards in this deck.
Unlock Deck
k this deck
40
A certain country's government economists have determined that the demand equation for soybeans in that country is given by 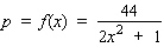 , where p is expressed in dollars/bushel and x, the quantity demanded each year, is measured in billions of bushels. The economists are forecasting a harvest of 1.8 billion bushels for the year, with a maximum error of 15% in their forecast.
, where p is expressed in dollars/bushel and x, the quantity demanded each year, is measured in billions of bushels. The economists are forecasting a harvest of 1.8 billion bushels for the year, with a maximum error of 15% in their forecast.
Determine the corresponding maximum error in the predicted price per bushel of soybeans. Round the answer to the nearest percent.
__________%
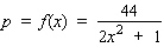 , where p is expressed in dollars/bushel and x, the quantity demanded each year, is measured in billions of bushels. The economists are forecasting a harvest of 1.8 billion bushels for the year, with a maximum error of 15% in their forecast.
, where p is expressed in dollars/bushel and x, the quantity demanded each year, is measured in billions of bushels. The economists are forecasting a harvest of 1.8 billion bushels for the year, with a maximum error of 15% in their forecast.Determine the corresponding maximum error in the predicted price per bushel of soybeans. Round the answer to the nearest percent.
__________%

Unlock Deck
Unlock for access to all 330 flashcards in this deck.
Unlock Deck
k this deck
41
Find 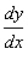 by implicit differentiation.
by implicit differentiation. 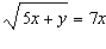
A)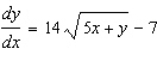
B)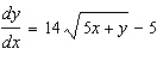
C)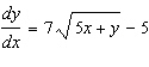
D)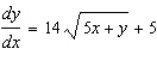
E)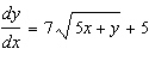
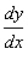 by implicit differentiation.
by implicit differentiation. 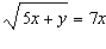
A)
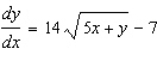
B)
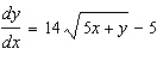
C)
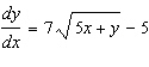
D)
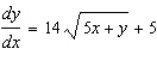
E)
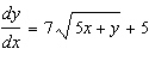

Unlock Deck
Unlock for access to all 330 flashcards in this deck.
Unlock Deck
k this deck
42
Find an equation of the tangent line to the graph of the function f defined by the equation at the indicated point. 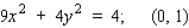
A)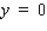
B)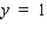
C)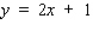
D)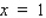
E)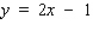
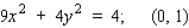
A)
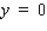
B)
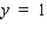
C)
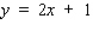
D)
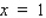
E)
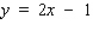

Unlock Deck
Unlock for access to all 330 flashcards in this deck.
Unlock Deck
k this deck
43
Find the differential of the function. 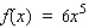
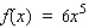

Unlock Deck
Unlock for access to all 330 flashcards in this deck.
Unlock Deck
k this deck
44
Let f be the function defined by 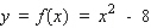 .
.
Find the differential of f.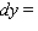 __________
__________
Find the approximate change in y if x changes from 3 to 3.07.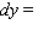 __________
__________
Find the actual change in y if x changes from 3 to 3.07.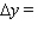 __________
__________
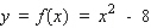 .
.Find the differential of f.
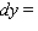 __________
__________Find the approximate change in y if x changes from 3 to 3.07.
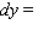 __________
__________Find the actual change in y if x changes from 3 to 3.07.
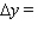 __________
__________
Unlock Deck
Unlock for access to all 330 flashcards in this deck.
Unlock Deck
k this deck
45
Find the differential of the function. 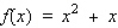
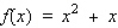

Unlock Deck
Unlock for access to all 330 flashcards in this deck.
Unlock Deck
k this deck
46
Find 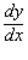 by implicit differentiation.
by implicit differentiation. 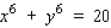
A)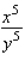
B)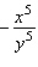
C)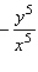
D)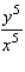
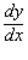 by implicit differentiation.
by implicit differentiation. 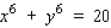
A)
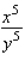
B)
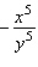
C)
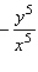
D)
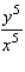

Unlock Deck
Unlock for access to all 330 flashcards in this deck.
Unlock Deck
k this deck
47
Find 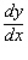 by implicit differentiation.
by implicit differentiation. 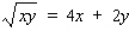
A)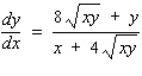
B)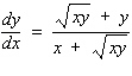
C)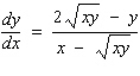
D)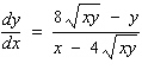
E)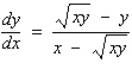
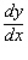 by implicit differentiation.
by implicit differentiation. 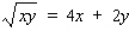
A)
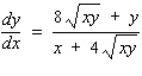
B)
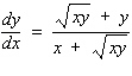
C)
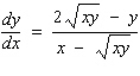
D)
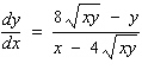
E)
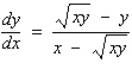

Unlock Deck
Unlock for access to all 330 flashcards in this deck.
Unlock Deck
k this deck
48
Find the derivative 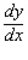 by solving the given implicit equation for y explicitly in terms of x.
by solving the given implicit equation for y explicitly in terms of x. 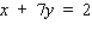
A)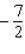
B)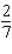
C)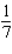
D)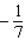
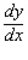 by solving the given implicit equation for y explicitly in terms of x.
by solving the given implicit equation for y explicitly in terms of x. 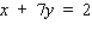
A)
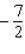
B)
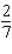
C)
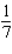
D)
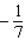

Unlock Deck
Unlock for access to all 330 flashcards in this deck.
Unlock Deck
k this deck
49
Two ships leave the same port at noon. Ship A sails north at 21 mph, and ship B sails east at 15 mph. How fast is the distance between them changing at 1 p.m.?
A)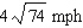
B)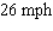
C)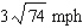
D)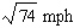
E)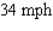
A)
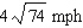
B)
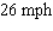
C)
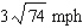
D)
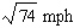
E)
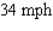

Unlock Deck
Unlock for access to all 330 flashcards in this deck.
Unlock Deck
k this deck
50
Find the second derivative 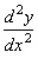 of the function defined implicitly by the equation.
of the function defined implicitly by the equation. 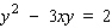
A)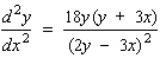
B)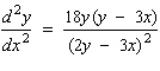
C)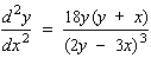
D)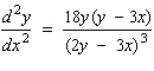
E)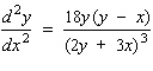
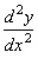 of the function defined implicitly by the equation.
of the function defined implicitly by the equation. 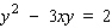
A)
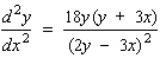
B)
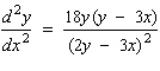
C)
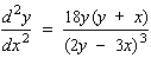
D)
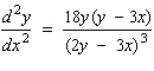
E)
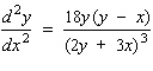

Unlock Deck
Unlock for access to all 330 flashcards in this deck.
Unlock Deck
k this deck
51
Find the differential of the function. 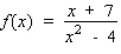
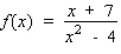

Unlock Deck
Unlock for access to all 330 flashcards in this deck.
Unlock Deck
k this deck
52
Find the differential of the function. 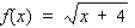
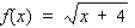

Unlock Deck
Unlock for access to all 330 flashcards in this deck.
Unlock Deck
k this deck
53
Find the derivative 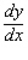 by solving the given implicit equation for y explicitly in terms of x.
by solving the given implicit equation for y explicitly in terms of x. 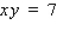
A)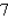
B)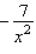
C)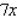
D)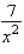
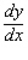 by solving the given implicit equation for y explicitly in terms of x.
by solving the given implicit equation for y explicitly in terms of x. 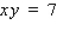
A)
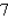
B)
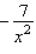
C)
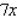
D)
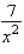

Unlock Deck
Unlock for access to all 330 flashcards in this deck.
Unlock Deck
k this deck
54
Find the differential of the function. 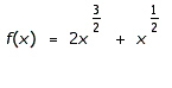
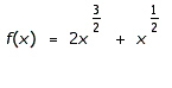

Unlock Deck
Unlock for access to all 330 flashcards in this deck.
Unlock Deck
k this deck
55
Find the differential of the function. 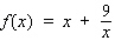
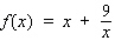

Unlock Deck
Unlock for access to all 330 flashcards in this deck.
Unlock Deck
k this deck
56
Find the differential of the function. 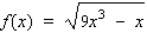
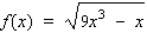

Unlock Deck
Unlock for access to all 330 flashcards in this deck.
Unlock Deck
k this deck
57
Find the differential of the function. 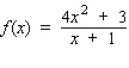
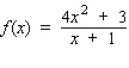

Unlock Deck
Unlock for access to all 330 flashcards in this deck.
Unlock Deck
k this deck
58
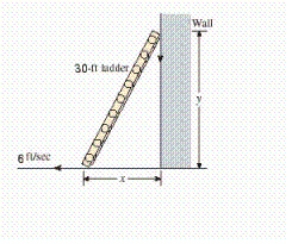
A 30-ft ladder leaning against a wall begins to slide. How fast is the top of the ladder sliding down the wall at the instant of time when the bottom of the ladder is 18 ft from the wall and sliding away from the wall at the rate of 6 ft/sec? Hint: Refer to the accompanying figure. By the Pythagorean theorem, 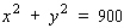 . Find
. Find 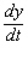 when
when 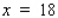 and
and 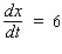 .
. 
A)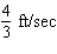
B)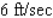
C)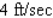
D)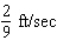
E)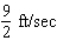
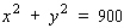 . Find
. Find 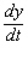 when
when 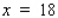 and
and 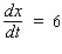 .
. 
A)
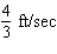
B)
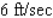
C)
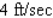
D)
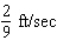
E)
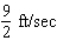

Unlock Deck
Unlock for access to all 330 flashcards in this deck.
Unlock Deck
k this deck
59
Find the derivative 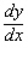 by solving the given implicit equation for y explicitly in terms of x.
by solving the given implicit equation for y explicitly in terms of x. 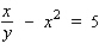
A)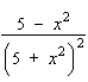
B)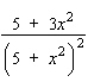
C)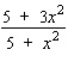
D)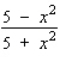
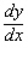 by solving the given implicit equation for y explicitly in terms of x.
by solving the given implicit equation for y explicitly in terms of x. 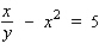
A)
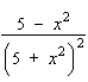
B)
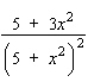
C)
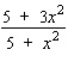
D)
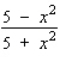

Unlock Deck
Unlock for access to all 330 flashcards in this deck.
Unlock Deck
k this deck
60
Suppose the wholesale price of a certain brand of medium-sized eggs p (in dollars/carton) is related to the weekly supply x (in thousands of cartons) by the equation 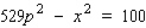 . If 23,000 cartons of eggs are available at the beginning of a certain week and the supply is falling at the rate of 800 cartons/week, at what rate is the wholesale price changing? (Hint: To find the value of p when
. If 23,000 cartons of eggs are available at the beginning of a certain week and the supply is falling at the rate of 800 cartons/week, at what rate is the wholesale price changing? (Hint: To find the value of p when 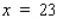 , solve the supply equation for p when
, solve the supply equation for p when 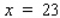 ).
).
A) Increasing at the rate of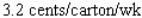
B) Increasing at the rate of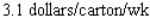
C) Dropping at the rate of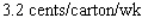
D) Dropping at the rate of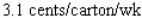
E) Dropping at the rate of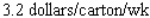
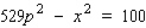 . If 23,000 cartons of eggs are available at the beginning of a certain week and the supply is falling at the rate of 800 cartons/week, at what rate is the wholesale price changing? (Hint: To find the value of p when
. If 23,000 cartons of eggs are available at the beginning of a certain week and the supply is falling at the rate of 800 cartons/week, at what rate is the wholesale price changing? (Hint: To find the value of p when 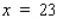 , solve the supply equation for p when
, solve the supply equation for p when 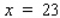 ).
).A) Increasing at the rate of
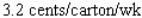
B) Increasing at the rate of
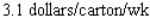
C) Dropping at the rate of
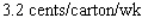
D) Dropping at the rate of
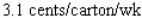
E) Dropping at the rate of
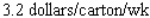

Unlock Deck
Unlock for access to all 330 flashcards in this deck.
Unlock Deck
k this deck
61
Find 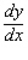 by implicit differentiation.
by implicit differentiation. 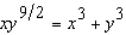
A)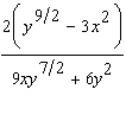
B)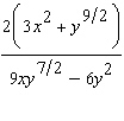
C)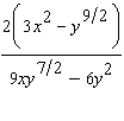
D)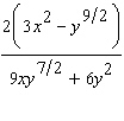
E)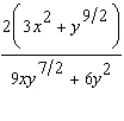
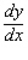 by implicit differentiation.
by implicit differentiation. 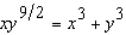
A)
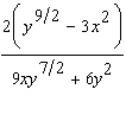
B)
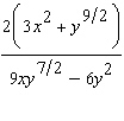
C)
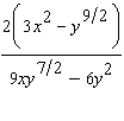
D)
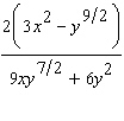
E)
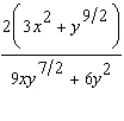

Unlock Deck
Unlock for access to all 330 flashcards in this deck.
Unlock Deck
k this deck
62
The demand function for a certain brand of compact disc is 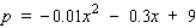 where p is the wholesale unit price in dollars and x is the quantity demanded each week, measured in units of a thousand. Compute the elasticity of demand and determine whether the demand is inelastic, unitary, or elastic when x = 13.
where p is the wholesale unit price in dollars and x is the quantity demanded each week, measured in units of a thousand. Compute the elasticity of demand and determine whether the demand is inelastic, unitary, or elastic when x = 13.
A) unitary
B) elastic
C) inelastic
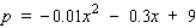 where p is the wholesale unit price in dollars and x is the quantity demanded each week, measured in units of a thousand. Compute the elasticity of demand and determine whether the demand is inelastic, unitary, or elastic when x = 13.
where p is the wholesale unit price in dollars and x is the quantity demanded each week, measured in units of a thousand. Compute the elasticity of demand and determine whether the demand is inelastic, unitary, or elastic when x = 13.A) unitary
B) elastic
C) inelastic

Unlock Deck
Unlock for access to all 330 flashcards in this deck.
Unlock Deck
k this deck
63
A spectator watches a rowing race from the edge of a river bank. The lead boat is moving in a straight line that is 90 ft from the river bank. If the boat is moving at a constant speed of 20 ft/sec, how fast is the boat moving away from the spectator when it is 400 ft past her?
A) 26.94 ft/sec
B) 17.28 ft/sec
C) 61.85 ft/sec
D) 19.51 ft/sec
A) 26.94 ft/sec
B) 17.28 ft/sec
C) 61.85 ft/sec
D) 19.51 ft/sec

Unlock Deck
Unlock for access to all 330 flashcards in this deck.
Unlock Deck
k this deck
64
Find 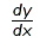 by implicit differentiation.
by implicit differentiation. 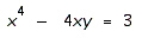
A)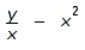
B)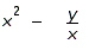
C)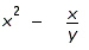
D)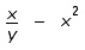
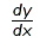 by implicit differentiation.
by implicit differentiation. 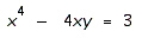
A)
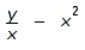
B)
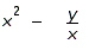
C)
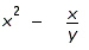
D)
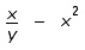

Unlock Deck
Unlock for access to all 330 flashcards in this deck.
Unlock Deck
k this deck
65
The demand equation for a certain brand of metal alloy audiocassette tape is 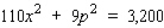 , where x represents the number (in thousands) of ten-packs demanded each week when the unit price is $p. How fast is the quantity demanded increasing when the unit price/ten-pack is $16 and the selling price is dropping at the rate of $.15/ten-pack/week? Round your answer to the nearest integer.
, where x represents the number (in thousands) of ten-packs demanded each week when the unit price is $p. How fast is the quantity demanded increasing when the unit price/ten-pack is $16 and the selling price is dropping at the rate of $.15/ten-pack/week? Round your answer to the nearest integer.
Hint: To find the value of x when p = 16, solve the equation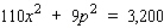 for x when p = 16.
for x when p = 16.
A) Increasing at the rate of 44 ten packs/wk.
B) Increasing at the rate of 71 ten packs/wk.
C) Increasing at the rate of 60 ten packs/wk.
D) Increasing at the rate of 69 ten packs/wk.
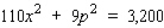 , where x represents the number (in thousands) of ten-packs demanded each week when the unit price is $p. How fast is the quantity demanded increasing when the unit price/ten-pack is $16 and the selling price is dropping at the rate of $.15/ten-pack/week? Round your answer to the nearest integer.
, where x represents the number (in thousands) of ten-packs demanded each week when the unit price is $p. How fast is the quantity demanded increasing when the unit price/ten-pack is $16 and the selling price is dropping at the rate of $.15/ten-pack/week? Round your answer to the nearest integer.Hint: To find the value of x when p = 16, solve the equation
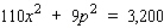 for x when p = 16.
for x when p = 16.A) Increasing at the rate of 44 ten packs/wk.
B) Increasing at the rate of 71 ten packs/wk.
C) Increasing at the rate of 60 ten packs/wk.
D) Increasing at the rate of 69 ten packs/wk.

Unlock Deck
Unlock for access to all 330 flashcards in this deck.
Unlock Deck
k this deck
66
Suppose the wholesale price of a certain brand of medium-sized eggs p (in dollars/carton) is related to the weekly supply x (in thousands of cartons) by the equation 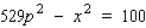 .
.
If 23,000 cartons of eggs are available at the beginning of a certain week and the supply is falling at the rate of 800 cartons/week, at what rate is the wholesale price changing? Round the answer to the nearest tenth. (Hint: To find the value of p when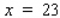 , solve the supply equation for p when
, solve the supply equation for p when 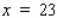 ).
).
Round the answer to the nearest tenth, if necessary.
__________
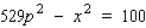 .
.If 23,000 cartons of eggs are available at the beginning of a certain week and the supply is falling at the rate of 800 cartons/week, at what rate is the wholesale price changing? Round the answer to the nearest tenth. (Hint: To find the value of p when
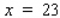 , solve the supply equation for p when
, solve the supply equation for p when 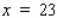 ).
).Round the answer to the nearest tenth, if necessary.
__________

Unlock Deck
Unlock for access to all 330 flashcards in this deck.
Unlock Deck
k this deck
67
A spectator watches a rowing race from the edge of a river bank. The lead boat is moving in a straight line that is 330 ft from the river bank. If the boat is moving at a constant speed of 20 ft/sec, how fast is the boat moving away from the spectator when it is 560 ft past her?
Round the answer to the nearest hundredth, if necessary.
__________ ft/sec
Round the answer to the nearest hundredth, if necessary.
__________ ft/sec

Unlock Deck
Unlock for access to all 330 flashcards in this deck.
Unlock Deck
k this deck
68
Find 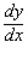 by implicit differentiation.
by implicit differentiation. 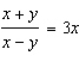
A)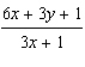
B)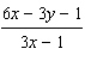
C)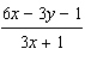
D)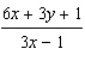
E)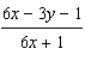
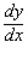 by implicit differentiation.
by implicit differentiation. 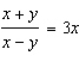
A)
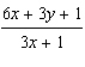
B)
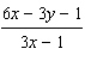
C)
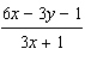
D)
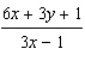
E)
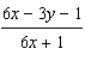

Unlock Deck
Unlock for access to all 330 flashcards in this deck.
Unlock Deck
k this deck
69
Find 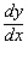 by implicit differentiation.
by implicit differentiation. 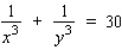
A)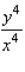
B)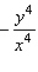
C)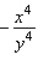
D)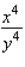
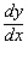 by implicit differentiation.
by implicit differentiation. 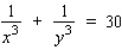
A)
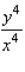
B)
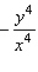
C)
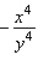
D)
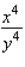

Unlock Deck
Unlock for access to all 330 flashcards in this deck.
Unlock Deck
k this deck
70
Find 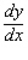 by implicit differentiation.
by implicit differentiation. 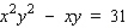
A)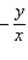
B)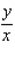
C)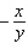
D)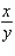
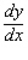 by implicit differentiation.
by implicit differentiation. 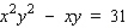
A)
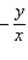
B)
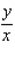
C)
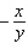
D)
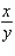

Unlock Deck
Unlock for access to all 330 flashcards in this deck.
Unlock Deck
k this deck
71
A 5-ft tall man is walking away from a street light 10 ft high at a speed of 5 ft/sec. How fast is the tip of his shadow moving along the ground?
A) 4 ft/sec
B) 8 ft/sec
C) 3 ft/sec
D) 10 ft/sec
A) 4 ft/sec
B) 8 ft/sec
C) 3 ft/sec
D) 10 ft/sec

Unlock Deck
Unlock for access to all 330 flashcards in this deck.
Unlock Deck
k this deck
72
Find 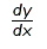 by implicit differentiation.
by implicit differentiation. 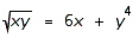
A)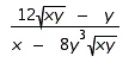
B)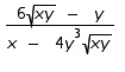
C)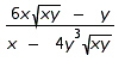
D)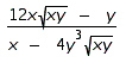
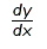 by implicit differentiation.
by implicit differentiation. 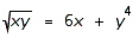
A)
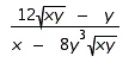
B)
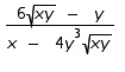
C)
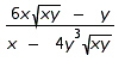
D)
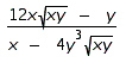

Unlock Deck
Unlock for access to all 330 flashcards in this deck.
Unlock Deck
k this deck
73
The base of a 25-ft ladder leaning against a wall begins to slide away from the wall. At the instant of time when the base is 24 ft from the wall, the base is moving at the rate of 7 ft/sec. How fast is the top of the ladder sliding down the wall at that instant of time?
Round the answer to the nearest tenth, if necessary.
__________ ft/sec
Round the answer to the nearest tenth, if necessary.
__________ ft/sec

Unlock Deck
Unlock for access to all 330 flashcards in this deck.
Unlock Deck
k this deck
74
A 5-ft tall man is walking away from a street light 10 ft high at a speed of 4 ft/sec . How fast is the tip of his shadow moving along the ground?
__________ ft/sec
__________ ft/sec

Unlock Deck
Unlock for access to all 330 flashcards in this deck.
Unlock Deck
k this deck
75
Find an equation of the tangent line to the graph of the function f defined by the given equation at the point 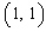 .
. 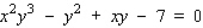
A)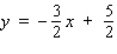
B)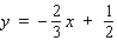
C)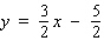
D)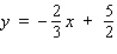
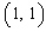 .
. 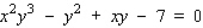
A)
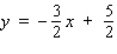
B)
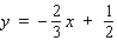
C)
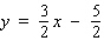
D)
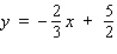

Unlock Deck
Unlock for access to all 330 flashcards in this deck.
Unlock Deck
k this deck
76
Suppose the quantity demanded weekly of the Super Titan radial tires is related to its unit price by the equation 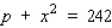 where p is measured in dollars and x is measured in units of a thousand. How fast is the quantity demanded changing when x = 13, p = 73, and the price/tire is increasing at the rate of $6/week?
where p is measured in dollars and x is measured in units of a thousand. How fast is the quantity demanded changing when x = 13, p = 73, and the price/tire is increasing at the rate of $6/week?
A) Dropping at the rate of 278 tires/wk.
B) Dropping at the rate of 231 tires/wk.
C) Dropping at the rate of 226 tires/wk.
D) Dropping at the rate of 268 tires/wk.
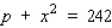 where p is measured in dollars and x is measured in units of a thousand. How fast is the quantity demanded changing when x = 13, p = 73, and the price/tire is increasing at the rate of $6/week?
where p is measured in dollars and x is measured in units of a thousand. How fast is the quantity demanded changing when x = 13, p = 73, and the price/tire is increasing at the rate of $6/week?A) Dropping at the rate of 278 tires/wk.
B) Dropping at the rate of 231 tires/wk.
C) Dropping at the rate of 226 tires/wk.
D) Dropping at the rate of 268 tires/wk.

Unlock Deck
Unlock for access to all 330 flashcards in this deck.
Unlock Deck
k this deck
77
The volume of a right-circular cylinder of radius r and height h is 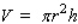 . Suppose the radius and height of the cylinder are changing with respect to time t. At a certain instant of time, the radius and height of the cylinder are 8 and 2 in. and are increasing at the rate of 0.5 and 0.2 in./sec, respectively. How fast is the volume of the cylinder increasing?
. Suppose the radius and height of the cylinder are changing with respect to time t. At a certain instant of time, the radius and height of the cylinder are 8 and 2 in. and are increasing at the rate of 0.5 and 0.2 in./sec, respectively. How fast is the volume of the cylinder increasing?
A)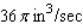
B)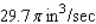
C)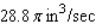
D)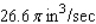
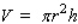 . Suppose the radius and height of the cylinder are changing with respect to time t. At a certain instant of time, the radius and height of the cylinder are 8 and 2 in. and are increasing at the rate of 0.5 and 0.2 in./sec, respectively. How fast is the volume of the cylinder increasing?
. Suppose the radius and height of the cylinder are changing with respect to time t. At a certain instant of time, the radius and height of the cylinder are 8 and 2 in. and are increasing at the rate of 0.5 and 0.2 in./sec, respectively. How fast is the volume of the cylinder increasing?A)
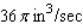
B)
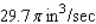
C)
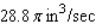
D)
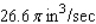

Unlock Deck
Unlock for access to all 330 flashcards in this deck.
Unlock Deck
k this deck
78
The base of a 5-ft ladder leaning against a wall begins to slide away from the wall. At the instant of time when the base is 4 ft from the wall, the base is moving at the rate of 6 ft/sec. How fast is the top of the ladder sliding down the wall at that instant of time?
A) 5.6 ft/sec
B) 6.5 ft/sec
C) 8 ft/sec
D) 9.3 ft/sec
A) 5.6 ft/sec
B) 6.5 ft/sec
C) 8 ft/sec
D) 9.3 ft/sec

Unlock Deck
Unlock for access to all 330 flashcards in this deck.
Unlock Deck
k this deck
79
Find 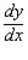 by implicit differentiation.
by implicit differentiation. 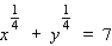
A)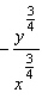
B)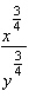
C)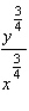
D)
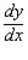 by implicit differentiation.
by implicit differentiation. 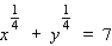
A)
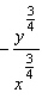
B)
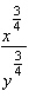
C)
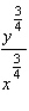
D)


Unlock Deck
Unlock for access to all 330 flashcards in this deck.
Unlock Deck
k this deck
80
In calm waters oil spilling from the ruptured hull of a grounded tanker spreads in all directions. If the area polluted is a circle and its radius is increasing at a rate of 3 ft/sec, determine how fast the area is increasing when the radius of the circle is 70 ft.
A)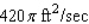
B)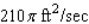
C)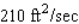
D)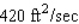
A)
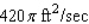
B)
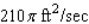
C)
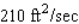
D)
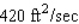

Unlock Deck
Unlock for access to all 330 flashcards in this deck.
Unlock Deck
k this deck


