Deck 8: Calculus of Several Variables
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/206
Play
Full screen (f)
Deck 8: Calculus of Several Variables
1
Evaluate the double integral 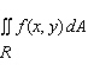 for the given function f(x, y) and the region R.
for the given function f(x, y) and the region R. 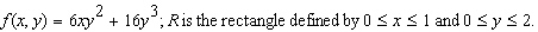
A) 9
B) 4
C) 72
D) 63
E) 8
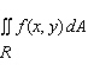 for the given function f(x, y) and the region R.
for the given function f(x, y) and the region R. 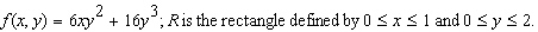
A) 9
B) 4
C) 72
D) 63
E) 8
72
2
Use a double integral to find the volume of the solid shown in the figure. 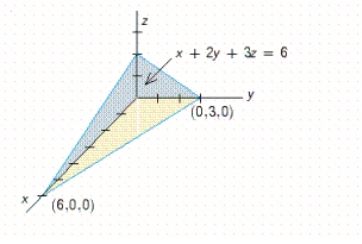
A) 14
B) 6
C) 4
D) 9

A) 14
B) 6
C) 4
D) 9
6
3
Evaluate the double integral 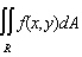 for the given function f(x, y) and the region R. f(x, y) = 6x + 6y; R is bounded by x = 0,
for the given function f(x, y) and the region R. f(x, y) = 6x + 6y; R is bounded by x = 0, 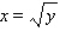 , y = 0 and y = 4.
, y = 0 and y = 4.
A)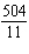
B)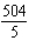
C)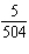
D)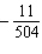
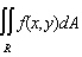 for the given function f(x, y) and the region R. f(x, y) = 6x + 6y; R is bounded by x = 0,
for the given function f(x, y) and the region R. f(x, y) = 6x + 6y; R is bounded by x = 0, 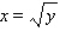 , y = 0 and y = 4.
, y = 0 and y = 4.A)
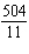
B)
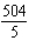
C)
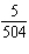
D)
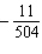
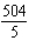
4
Use a double integral to find the volume of the solid shown in the figure. 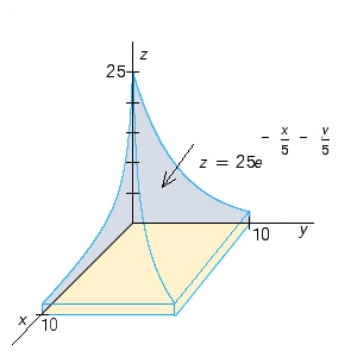
A)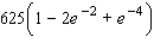
B)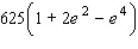
C)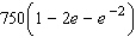
D)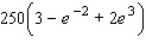

A)
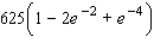
B)
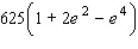
C)
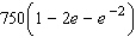
D)
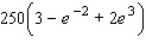

Unlock Deck
Unlock for access to all 206 flashcards in this deck.
Unlock Deck
k this deck
5
Evaluate the double integral 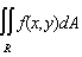 for the given function f(x, y) and the region R. f(x, y) = 4x + 2y; R is bounded by x = 0, x = 4, y = 0 and y = x.
for the given function f(x, y) and the region R. f(x, y) = 4x + 2y; R is bounded by x = 0, x = 4, y = 0 and y = x.
A)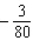
B)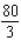
C)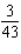
D)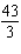
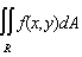 for the given function f(x, y) and the region R. f(x, y) = 4x + 2y; R is bounded by x = 0, x = 4, y = 0 and y = x.
for the given function f(x, y) and the region R. f(x, y) = 4x + 2y; R is bounded by x = 0, x = 4, y = 0 and y = x.A)
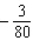
B)
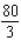
C)
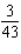
D)
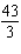

Unlock Deck
Unlock for access to all 206 flashcards in this deck.
Unlock Deck
k this deck
6
Evaluate the double integral 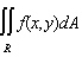 for the given function f(x, y) and the region R. f(x, y) = 5
for the given function f(x, y) and the region R. f(x, y) = 5 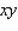 ; R is bounded by the lines x = 1, y = 0 and y = x.
; R is bounded by the lines x = 1, y = 0 and y = x.
A)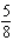
B)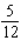
C)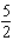
D)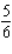
E)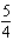
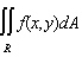 for the given function f(x, y) and the region R. f(x, y) = 5
for the given function f(x, y) and the region R. f(x, y) = 5 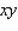 ; R is bounded by the lines x = 1, y = 0 and y = x.
; R is bounded by the lines x = 1, y = 0 and y = x.A)
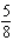
B)
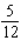
C)
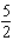
D)
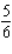
E)
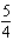

Unlock Deck
Unlock for access to all 206 flashcards in this deck.
Unlock Deck
k this deck
7
Evaluate the double integral 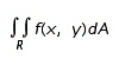 for the given function f(x, y) and the region R.
for the given function f(x, y) and the region R. 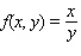 ; R is the rectangle defined by
; R is the rectangle defined by 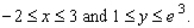
A)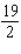
B)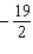
C)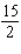
D)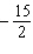
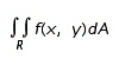 for the given function f(x, y) and the region R.
for the given function f(x, y) and the region R. 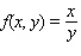 ; R is the rectangle defined by
; R is the rectangle defined by 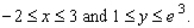
A)
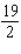
B)
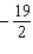
C)
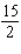
D)
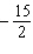

Unlock Deck
Unlock for access to all 206 flashcards in this deck.
Unlock Deck
k this deck
8
Evaluate the double integral 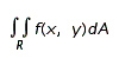 for the given function f(x, y) and the region R.
for the given function f(x, y) and the region R. 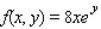 ; R is bounded by x = 0, x = 1, y = 0 and y = x.
; R is bounded by x = 0, x = 1, y = 0 and y = x.
A) 4
B) 2e
C) - 2
D) - 4
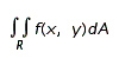 for the given function f(x, y) and the region R.
for the given function f(x, y) and the region R. 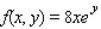 ; R is bounded by x = 0, x = 1, y = 0 and y = x.
; R is bounded by x = 0, x = 1, y = 0 and y = x.A) 4
B) 2e
C) - 2
D) - 4

Unlock Deck
Unlock for access to all 206 flashcards in this deck.
Unlock Deck
k this deck
9
Evaluate the double integral 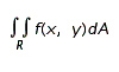 for the given function f(x, y) and the region R.
for the given function f(x, y) and the region R. 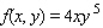 ; R is the rectangle defined by
; R is the rectangle defined by 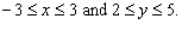
A) 5
B) 0
C) 3
D) - 5
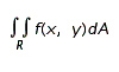 for the given function f(x, y) and the region R.
for the given function f(x, y) and the region R. 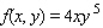 ; R is the rectangle defined by
; R is the rectangle defined by 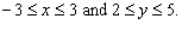
A) 5
B) 0
C) 3
D) - 5

Unlock Deck
Unlock for access to all 206 flashcards in this deck.
Unlock Deck
k this deck
10
Use a double integral to find the volume of the solid shown in the figure. 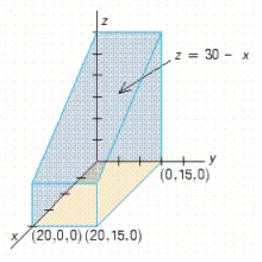
A) 5,996
B) 5,994
C) 6,000
D) 6,008

A) 5,996
B) 5,994
C) 6,000
D) 6,008

Unlock Deck
Unlock for access to all 206 flashcards in this deck.
Unlock Deck
k this deck
11
Evaluate the double integral 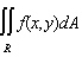 for the given function f(x, y) and the region R. f(x, y) = 2y + x; R is the rectangle defined by
for the given function f(x, y) and the region R. f(x, y) = 2y + x; R is the rectangle defined by 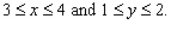
A)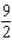
B)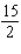
C)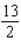
D) 26
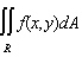 for the given function f(x, y) and the region R. f(x, y) = 2y + x; R is the rectangle defined by
for the given function f(x, y) and the region R. f(x, y) = 2y + x; R is the rectangle defined by 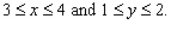
A)
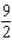
B)
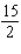
C)
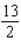
D) 26

Unlock Deck
Unlock for access to all 206 flashcards in this deck.
Unlock Deck
k this deck
12
Evaluate the double integral 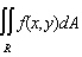 for the given function f(x, y) and the region R.
for the given function f(x, y) and the region R. 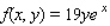 ; R is bounded by
; R is bounded by 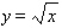 and y = x.
and y = x.
A)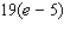
B)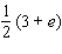
C)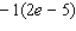
D)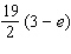
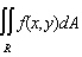 for the given function f(x, y) and the region R.
for the given function f(x, y) and the region R. 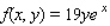 ; R is bounded by
; R is bounded by 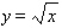 and y = x.
and y = x.A)
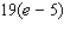
B)
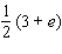
C)
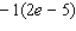
D)
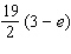

Unlock Deck
Unlock for access to all 206 flashcards in this deck.
Unlock Deck
k this deck
13
Evaluate the double integral 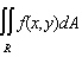 for the given function f(x, y) and the region R. f(x, y) = 6x + 12y; R is bounded by x = 1, x = 3, y = 0 and y = x + 1.
for the given function f(x, y) and the region R. f(x, y) = 6x + 12y; R is bounded by x = 1, x = 3, y = 0 and y = x + 1.
A)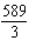
B)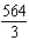
C)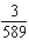
D)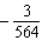
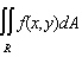 for the given function f(x, y) and the region R. f(x, y) = 6x + 12y; R is bounded by x = 1, x = 3, y = 0 and y = x + 1.
for the given function f(x, y) and the region R. f(x, y) = 6x + 12y; R is bounded by x = 1, x = 3, y = 0 and y = x + 1.A)
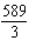
B)
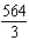
C)
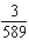
D)
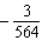

Unlock Deck
Unlock for access to all 206 flashcards in this deck.
Unlock Deck
k this deck
14
Find the volume of the solid bounded above by the surface z = f(x, y)
And below by the plane region R.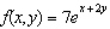 ; R is the triangle with vertices (0, 0), (5, 0) and (0, 5).
; R is the triangle with vertices (0, 0), (5, 0) and (0, 5).
A)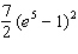
B)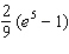
C)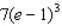
And below by the plane region R.
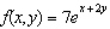 ; R is the triangle with vertices (0, 0), (5, 0) and (0, 5).
; R is the triangle with vertices (0, 0), (5, 0) and (0, 5).A)
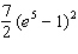
B)
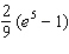
C)
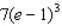

Unlock Deck
Unlock for access to all 206 flashcards in this deck.
Unlock Deck
k this deck
15
Use a double integral to find the volume of the solid shown in the figure. 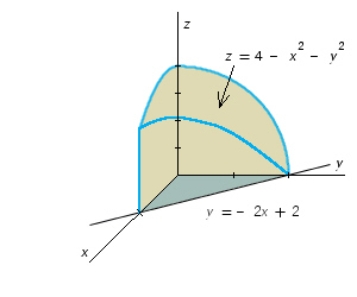
A)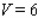
B)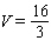
C)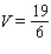
D)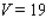
E)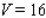

A)
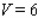
B)
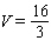
C)
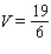
D)
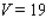
E)
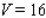

Unlock Deck
Unlock for access to all 206 flashcards in this deck.
Unlock Deck
k this deck
16
Evaluate the double integral 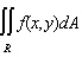 for the given function f(x, y) and the region R.
for the given function f(x, y) and the region R. 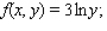 R is the rectangle defined by
R is the rectangle defined by 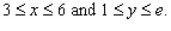
A) 10e
B) 9
C) - 9e
D) - 10
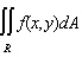 for the given function f(x, y) and the region R.
for the given function f(x, y) and the region R. 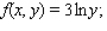 R is the rectangle defined by
R is the rectangle defined by 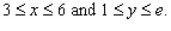
A) 10e
B) 9
C) - 9e
D) - 10

Unlock Deck
Unlock for access to all 206 flashcards in this deck.
Unlock Deck
k this deck
17
Evaluate the double integral 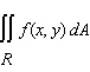 for the given function f(x, y) and the region R.
for the given function f(x, y) and the region R. 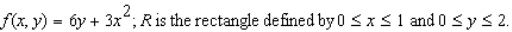
A) 14
B) 13
C) 11
D) 18
E) 2
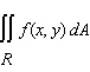 for the given function f(x, y) and the region R.
for the given function f(x, y) and the region R. 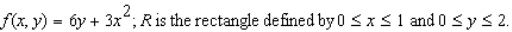
A) 14
B) 13
C) 11
D) 18
E) 2

Unlock Deck
Unlock for access to all 206 flashcards in this deck.
Unlock Deck
k this deck
18
Find the volume of the solid bounded above by the surface z = f(x, y)
And below by the plane region R.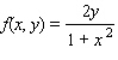 ; R is the region bounded by
; R is the region bounded by 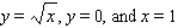 .
.
A)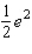
B)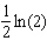
C)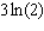
And below by the plane region R.
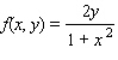 ; R is the region bounded by
; R is the region bounded by 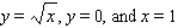 .
.A)
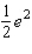
B)
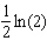
C)
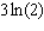

Unlock Deck
Unlock for access to all 206 flashcards in this deck.
Unlock Deck
k this deck
19
Evaluate the double integral 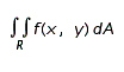 for the function
for the function 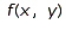 and the region
and the region 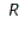 .
. 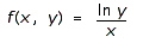 and
and  is the rectangle defined by
is the rectangle defined by 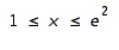 and
and 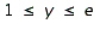 .
.
A)
B)
C)
D)
E)
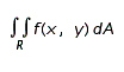 for the function
for the function 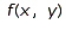 and the region
and the region 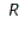 .
. 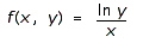 and
and  is the rectangle defined by
is the rectangle defined by 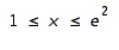 and
and 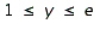 .
.A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 206 flashcards in this deck.
Unlock Deck
k this deck
20
Evaluate the double integral 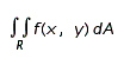 for the function
for the function 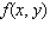 and the region
and the region 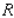 .
. 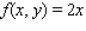 and
and 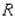 is bounded by
is bounded by 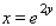 ,
, 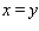 ,
, 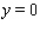 and
and 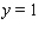 .
.
A)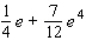
B)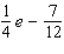
C)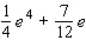
D)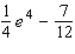
E)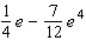
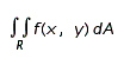 for the function
for the function 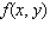 and the region
and the region  .
. 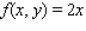 and
and 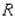 is bounded by
is bounded by 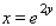 ,
, 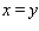 ,
, 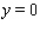 and
and 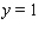 .
.A)
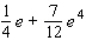
B)
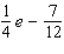
C)
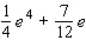
D)
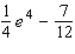
E)
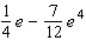

Unlock Deck
Unlock for access to all 206 flashcards in this deck.
Unlock Deck
k this deck
21
Find the average value of the given function f(x, y)
Over the plane region R.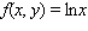 ; R is the region bounded by the graph of y = 2x and y = 0 from x = 1 to x = 3.
; R is the region bounded by the graph of y = 2x and y = 0 from x = 1 to x = 3.
A)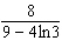
B)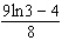
C)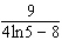
D)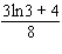
Over the plane region R.
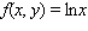 ; R is the region bounded by the graph of y = 2x and y = 0 from x = 1 to x = 3.
; R is the region bounded by the graph of y = 2x and y = 0 from x = 1 to x = 3.A)
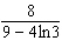
B)
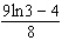
C)
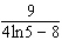
D)
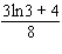

Unlock Deck
Unlock for access to all 206 flashcards in this deck.
Unlock Deck
k this deck
22
The Country Workshop's total weekly profit (in dollars) realized in manufacturing and selling its rolltop desks is given by the profit function 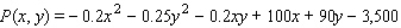 where
where 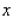 stands for the number of finished units and
stands for the number of finished units and 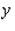 stands for the number of unfinished units manufactured and sold each week. Find the average weekly profit if the number of finished units manufactured and sold varies between
stands for the number of unfinished units manufactured and sold each week. Find the average weekly profit if the number of finished units manufactured and sold varies between 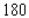 and
and 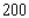 and the number of unfinished units varies between
and the number of unfinished units varies between 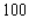 and
and 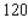 per week. Please round your answer to the nearest dollar, if necessary.
per week. Please round your answer to the nearest dollar, if necessary.  $__________ per week.
$__________ per week.
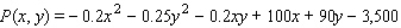 where
where 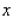 stands for the number of finished units and
stands for the number of finished units and 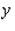 stands for the number of unfinished units manufactured and sold each week. Find the average weekly profit if the number of finished units manufactured and sold varies between
stands for the number of unfinished units manufactured and sold each week. Find the average weekly profit if the number of finished units manufactured and sold varies between 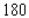 and
and 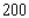 and the number of unfinished units varies between
and the number of unfinished units varies between 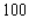 and
and 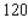 per week. Please round your answer to the nearest dollar, if necessary.
per week. Please round your answer to the nearest dollar, if necessary. 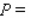 $__________ per week.
$__________ per week.
Unlock Deck
Unlock for access to all 206 flashcards in this deck.
Unlock Deck
k this deck
23
Use a double integral to find the volume of the solid shown in the figure. 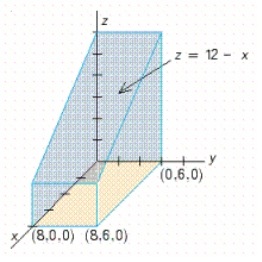


Unlock Deck
Unlock for access to all 206 flashcards in this deck.
Unlock Deck
k this deck
24
Evaluate the double integral 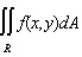 for the given function f(x, y) and the region R.
for the given function f(x, y) and the region R.
f(x, y) = 4x + 8y; R is bounded by x = 1, x = 3, y = 0 and y = x + 1.
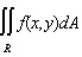 for the given function f(x, y) and the region R.
for the given function f(x, y) and the region R.f(x, y) = 4x + 8y; R is bounded by x = 1, x = 3, y = 0 and y = x + 1.

Unlock Deck
Unlock for access to all 206 flashcards in this deck.
Unlock Deck
k this deck
25
Evaluate the double integral 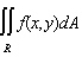 for the given function f(x, y) and the region R.
for the given function f(x, y) and the region R. 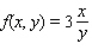 ; R is the rectangle defined by
; R is the rectangle defined by 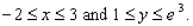
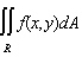 for the given function f(x, y) and the region R.
for the given function f(x, y) and the region R. 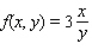 ; R is the rectangle defined by
; R is the rectangle defined by 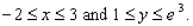

Unlock Deck
Unlock for access to all 206 flashcards in this deck.
Unlock Deck
k this deck
26
Evaluate the double integral 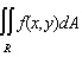 for the given function f(x, y) and the region R.
for the given function f(x, y) and the region R.
f(x, y) = 3x + 4y; R is bounded by x = 0, x = 1, y = 0 and y = x.
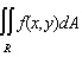 for the given function f(x, y) and the region R.
for the given function f(x, y) and the region R.f(x, y) = 3x + 4y; R is bounded by x = 0, x = 1, y = 0 and y = x.

Unlock Deck
Unlock for access to all 206 flashcards in this deck.
Unlock Deck
k this deck
27
Evaluate the double integral 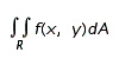 for the given function f(x, y) and the region R.
for the given function f(x, y) and the region R.
f(x, y) = 2x + 2y; R is bounded by x = 0,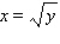 , y = 0 and y = 4.
, y = 0 and y = 4.
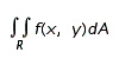 for the given function f(x, y) and the region R.
for the given function f(x, y) and the region R.f(x, y) = 2x + 2y; R is bounded by x = 0,
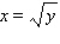 , y = 0 and y = 4.
, y = 0 and y = 4.
Unlock Deck
Unlock for access to all 206 flashcards in this deck.
Unlock Deck
k this deck
28
Find the average value of the function 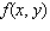 over the plane region
over the plane region 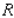 .
. 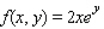 and
and 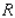 is the triangle with vertices (0, 0), (0, 1) and (1, 1).
is the triangle with vertices (0, 0), (0, 1) and (1, 1).
A)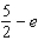
B)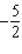
C)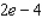
D) e
E)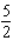
 over the plane region
over the plane region  .
. 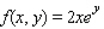 and
and 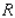 is the triangle with vertices (0, 0), (0, 1) and (1, 1).
is the triangle with vertices (0, 0), (0, 1) and (1, 1).A)
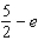
B)
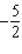
C)
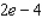
D) e
E)
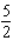

Unlock Deck
Unlock for access to all 206 flashcards in this deck.
Unlock Deck
k this deck
29
Evaluate the double integral 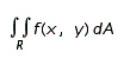 for the function
for the function 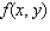 and the region
and the region 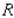 .
. 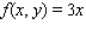 and
and 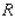 is bounded by
is bounded by 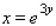 ,
, 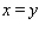 ,
, 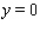 and
and 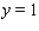 .
.
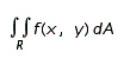 for the function
for the function 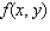 and the region
and the region  .
. 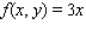 and
and 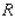 is bounded by
is bounded by 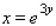 ,
, 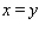 ,
, 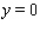 and
and 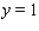 .
.
Unlock Deck
Unlock for access to all 206 flashcards in this deck.
Unlock Deck
k this deck
30
Evaluate the double integral 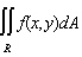 for the given function f(x, y) and the region R.
for the given function f(x, y) and the region R. 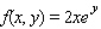 ; R is bounded by x = 0, x = 1, y = 0 and y = x.
; R is bounded by x = 0, x = 1, y = 0 and y = x.
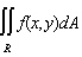 for the given function f(x, y) and the region R.
for the given function f(x, y) and the region R. 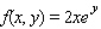 ; R is bounded by x = 0, x = 1, y = 0 and y = x.
; R is bounded by x = 0, x = 1, y = 0 and y = x.
Unlock Deck
Unlock for access to all 206 flashcards in this deck.
Unlock Deck
k this deck
31
Find the average value of the given function f(x, y)
Over the plane region R.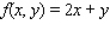 ; R is the triangle with vertices (0, 0), (5, 0) and (5, 5).
; R is the triangle with vertices (0, 0), (5, 0) and (5, 5).
A)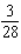
B)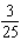
C)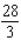
D)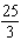
Over the plane region R.
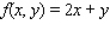 ; R is the triangle with vertices (0, 0), (5, 0) and (5, 5).
; R is the triangle with vertices (0, 0), (5, 0) and (5, 5).A)
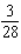
B)
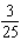
C)
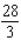
D)

Unlock Deck
Unlock for access to all 206 flashcards in this deck.
Unlock Deck
k this deck
32
Evaluate the double integral 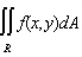 for the given function f(x, y) and the region R.
for the given function f(x, y) and the region R. 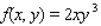 ; R is the rectangle defined by
; R is the rectangle defined by 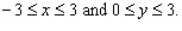
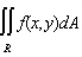 for the given function f(x, y) and the region R.
for the given function f(x, y) and the region R. 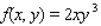 ; R is the rectangle defined by
; R is the rectangle defined by 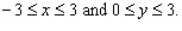

Unlock Deck
Unlock for access to all 206 flashcards in this deck.
Unlock Deck
k this deck
33
Evaluate the double integral 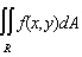 for the given function f(x, y) and the region R.
for the given function f(x, y) and the region R.
f(x, y) = 2y + 3x; R is the rectangle defined by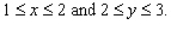
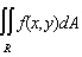 for the given function f(x, y) and the region R.
for the given function f(x, y) and the region R.f(x, y) = 2y + 3x; R is the rectangle defined by
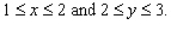

Unlock Deck
Unlock for access to all 206 flashcards in this deck.
Unlock Deck
k this deck
34
The population density of a certain city is given by the function 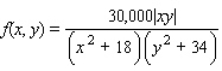 where the origin (0, 0) gives the location of the government center. Find the population inside the rectangular area described by
where the origin (0, 0) gives the location of the government center. Find the population inside the rectangular area described by 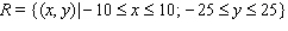
A)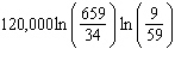
B)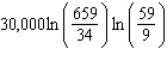
C)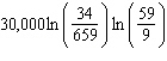
D)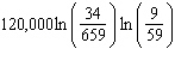
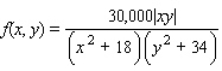 where the origin (0, 0) gives the location of the government center. Find the population inside the rectangular area described by
where the origin (0, 0) gives the location of the government center. Find the population inside the rectangular area described by 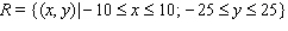
A)
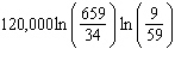
B)
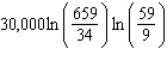
C)
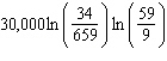
D)
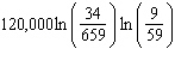

Unlock Deck
Unlock for access to all 206 flashcards in this deck.
Unlock Deck
k this deck
35
Use a double integral to find the volume of the solid shown in the figure. 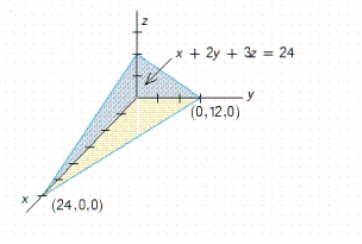


Unlock Deck
Unlock for access to all 206 flashcards in this deck.
Unlock Deck
k this deck
36
Determine whether the statement is true or false. If it is true, explain why it is true. If it is false, give an example to show why it is false. If h(x, y) = f(x)g(y), where f is continuous on [a, b] and g is continuous on [c, d], then ![<strong>Determine whether the statement is true or false. If it is true, explain why it is true. If it is false, give an example to show why it is false. If h(x, y) = f(x)g(y), where f is continuous on [a, b] and g is continuous on [c, d], then where </strong> A) From the definition follows , so the statement is true. B) From the definition follows , so the statement is false. C) From the definition follows , so the statement is false.](https://storage.examlex.com/TB6026/11eaa8b1_d973_bd69_b1b6_59b71036c616_TB6026_11.jpg) where
where ![<strong>Determine whether the statement is true or false. If it is true, explain why it is true. If it is false, give an example to show why it is false. If h(x, y) = f(x)g(y), where f is continuous on [a, b] and g is continuous on [c, d], then where </strong> A) From the definition follows , so the statement is true. B) From the definition follows , so the statement is false. C) From the definition follows , so the statement is false.](https://storage.examlex.com/TB6026/11eaa8b1_d973_bd6a_b1b6_a3016793e416_TB6026_11.jpg)
A) From the definition follows![<strong>Determine whether the statement is true or false. If it is true, explain why it is true. If it is false, give an example to show why it is false. If h(x, y) = f(x)g(y), where f is continuous on [a, b] and g is continuous on [c, d], then where </strong> A) From the definition follows , so the statement is true. B) From the definition follows , so the statement is false. C) From the definition follows , so the statement is false.](https://storage.examlex.com/TB6026/11eaa8b1_d973_e47b_b1b6_5f1d86d3579e_TB6026_11.jpg)
![<strong>Determine whether the statement is true or false. If it is true, explain why it is true. If it is false, give an example to show why it is false. If h(x, y) = f(x)g(y), where f is continuous on [a, b] and g is continuous on [c, d], then where </strong> A) From the definition follows , so the statement is true. B) From the definition follows , so the statement is false. C) From the definition follows , so the statement is false.](https://storage.examlex.com/TB6026/11eaa8b1_d974_0b8c_b1b6_7daad9a35ffe_TB6026_11.jpg)
![<strong>Determine whether the statement is true or false. If it is true, explain why it is true. If it is false, give an example to show why it is false. If h(x, y) = f(x)g(y), where f is continuous on [a, b] and g is continuous on [c, d], then where </strong> A) From the definition follows , so the statement is true. B) From the definition follows , so the statement is false. C) From the definition follows , so the statement is false.](https://storage.examlex.com/TB6026/11eaa8b1_d974_0b8d_b1b6_e943e9ba6017_TB6026_11.jpg)
![<strong>Determine whether the statement is true or false. If it is true, explain why it is true. If it is false, give an example to show why it is false. If h(x, y) = f(x)g(y), where f is continuous on [a, b] and g is continuous on [c, d], then where </strong> A) From the definition follows , so the statement is true. B) From the definition follows , so the statement is false. C) From the definition follows , so the statement is false.](https://storage.examlex.com/TB6026/11eaa8b1_d974_329e_b1b6_e14b4cf7232b_TB6026_11.jpg)
![<strong>Determine whether the statement is true or false. If it is true, explain why it is true. If it is false, give an example to show why it is false. If h(x, y) = f(x)g(y), where f is continuous on [a, b] and g is continuous on [c, d], then where </strong> A) From the definition follows , so the statement is true. B) From the definition follows , so the statement is false. C) From the definition follows , so the statement is false.](https://storage.examlex.com/TB6026/11eaa8b1_d974_59af_b1b6_399bcbacf9f5_TB6026_11.jpg) , so the statement is true.
, so the statement is true.
B) From the definition follows![<strong>Determine whether the statement is true or false. If it is true, explain why it is true. If it is false, give an example to show why it is false. If h(x, y) = f(x)g(y), where f is continuous on [a, b] and g is continuous on [c, d], then where </strong> A) From the definition follows , so the statement is true. B) From the definition follows , so the statement is false. C) From the definition follows , so the statement is false.](https://storage.examlex.com/TB6026/11eaa8b1_d974_80c0_b1b6_b1d55a522883_TB6026_11.jpg)
![<strong>Determine whether the statement is true or false. If it is true, explain why it is true. If it is false, give an example to show why it is false. If h(x, y) = f(x)g(y), where f is continuous on [a, b] and g is continuous on [c, d], then where </strong> A) From the definition follows , so the statement is true. B) From the definition follows , so the statement is false. C) From the definition follows , so the statement is false.](https://storage.examlex.com/TB6026/11eaa8b1_d974_80c1_b1b6_73bf039417a5_TB6026_11.jpg)
![<strong>Determine whether the statement is true or false. If it is true, explain why it is true. If it is false, give an example to show why it is false. If h(x, y) = f(x)g(y), where f is continuous on [a, b] and g is continuous on [c, d], then where </strong> A) From the definition follows , so the statement is true. B) From the definition follows , so the statement is false. C) From the definition follows , so the statement is false.](https://storage.examlex.com/TB6026/11eaa8b1_d974_a7d2_b1b6_15c2ba687213_TB6026_11.jpg)
![<strong>Determine whether the statement is true or false. If it is true, explain why it is true. If it is false, give an example to show why it is false. If h(x, y) = f(x)g(y), where f is continuous on [a, b] and g is continuous on [c, d], then where </strong> A) From the definition follows , so the statement is true. B) From the definition follows , so the statement is false. C) From the definition follows , so the statement is false.](https://storage.examlex.com/TB6026/11eaa8b1_d974_a7d3_b1b6_5d27e7597df5_TB6026_11.jpg)
![<strong>Determine whether the statement is true or false. If it is true, explain why it is true. If it is false, give an example to show why it is false. If h(x, y) = f(x)g(y), where f is continuous on [a, b] and g is continuous on [c, d], then where </strong> A) From the definition follows , so the statement is true. B) From the definition follows , so the statement is false. C) From the definition follows , so the statement is false.](https://storage.examlex.com/TB6026/11eaa8b1_d974_cee4_b1b6_47cf4c44e522_TB6026_11.jpg) , so the statement is false.
, so the statement is false.
C) From the definition follows![<strong>Determine whether the statement is true or false. If it is true, explain why it is true. If it is false, give an example to show why it is false. If h(x, y) = f(x)g(y), where f is continuous on [a, b] and g is continuous on [c, d], then where </strong> A) From the definition follows , so the statement is true. B) From the definition follows , so the statement is false. C) From the definition follows , so the statement is false.](https://storage.examlex.com/TB6026/11eaa8b1_d974_f5f5_b1b6_95e64b3a9da5_TB6026_11.jpg)
![<strong>Determine whether the statement is true or false. If it is true, explain why it is true. If it is false, give an example to show why it is false. If h(x, y) = f(x)g(y), where f is continuous on [a, b] and g is continuous on [c, d], then where </strong> A) From the definition follows , so the statement is true. B) From the definition follows , so the statement is false. C) From the definition follows , so the statement is false.](https://storage.examlex.com/TB6026/11eaa8b1_d975_1d06_b1b6_cb2ce721719e_TB6026_11.jpg)
![<strong>Determine whether the statement is true or false. If it is true, explain why it is true. If it is false, give an example to show why it is false. If h(x, y) = f(x)g(y), where f is continuous on [a, b] and g is continuous on [c, d], then where </strong> A) From the definition follows , so the statement is true. B) From the definition follows , so the statement is false. C) From the definition follows , so the statement is false.](https://storage.examlex.com/TB6026/11eaa8b1_d975_1d07_b1b6_f91325f40d4a_TB6026_11.jpg)
![<strong>Determine whether the statement is true or false. If it is true, explain why it is true. If it is false, give an example to show why it is false. If h(x, y) = f(x)g(y), where f is continuous on [a, b] and g is continuous on [c, d], then where </strong> A) From the definition follows , so the statement is true. B) From the definition follows , so the statement is false. C) From the definition follows , so the statement is false.](https://storage.examlex.com/TB6026/11eaa8b1_d975_4418_b1b6_75554aad7fa0_TB6026_11.jpg)
![<strong>Determine whether the statement is true or false. If it is true, explain why it is true. If it is false, give an example to show why it is false. If h(x, y) = f(x)g(y), where f is continuous on [a, b] and g is continuous on [c, d], then where </strong> A) From the definition follows , so the statement is true. B) From the definition follows , so the statement is false. C) From the definition follows , so the statement is false.](https://storage.examlex.com/TB6026/11eaa8b1_d975_4419_b1b6_01cc3848185a_TB6026_11.jpg) , so the statement is false.
, so the statement is false.
![<strong>Determine whether the statement is true or false. If it is true, explain why it is true. If it is false, give an example to show why it is false. If h(x, y) = f(x)g(y), where f is continuous on [a, b] and g is continuous on [c, d], then where </strong> A) From the definition follows , so the statement is true. B) From the definition follows , so the statement is false. C) From the definition follows , so the statement is false.](https://storage.examlex.com/TB6026/11eaa8b1_d973_bd69_b1b6_59b71036c616_TB6026_11.jpg) where
where ![<strong>Determine whether the statement is true or false. If it is true, explain why it is true. If it is false, give an example to show why it is false. If h(x, y) = f(x)g(y), where f is continuous on [a, b] and g is continuous on [c, d], then where </strong> A) From the definition follows , so the statement is true. B) From the definition follows , so the statement is false. C) From the definition follows , so the statement is false.](https://storage.examlex.com/TB6026/11eaa8b1_d973_bd6a_b1b6_a3016793e416_TB6026_11.jpg)
A) From the definition follows
![<strong>Determine whether the statement is true or false. If it is true, explain why it is true. If it is false, give an example to show why it is false. If h(x, y) = f(x)g(y), where f is continuous on [a, b] and g is continuous on [c, d], then where </strong> A) From the definition follows , so the statement is true. B) From the definition follows , so the statement is false. C) From the definition follows , so the statement is false.](https://storage.examlex.com/TB6026/11eaa8b1_d973_e47b_b1b6_5f1d86d3579e_TB6026_11.jpg)
![<strong>Determine whether the statement is true or false. If it is true, explain why it is true. If it is false, give an example to show why it is false. If h(x, y) = f(x)g(y), where f is continuous on [a, b] and g is continuous on [c, d], then where </strong> A) From the definition follows , so the statement is true. B) From the definition follows , so the statement is false. C) From the definition follows , so the statement is false.](https://storage.examlex.com/TB6026/11eaa8b1_d974_0b8c_b1b6_7daad9a35ffe_TB6026_11.jpg)
![<strong>Determine whether the statement is true or false. If it is true, explain why it is true. If it is false, give an example to show why it is false. If h(x, y) = f(x)g(y), where f is continuous on [a, b] and g is continuous on [c, d], then where </strong> A) From the definition follows , so the statement is true. B) From the definition follows , so the statement is false. C) From the definition follows , so the statement is false.](https://storage.examlex.com/TB6026/11eaa8b1_d974_0b8d_b1b6_e943e9ba6017_TB6026_11.jpg)
![<strong>Determine whether the statement is true or false. If it is true, explain why it is true. If it is false, give an example to show why it is false. If h(x, y) = f(x)g(y), where f is continuous on [a, b] and g is continuous on [c, d], then where </strong> A) From the definition follows , so the statement is true. B) From the definition follows , so the statement is false. C) From the definition follows , so the statement is false.](https://storage.examlex.com/TB6026/11eaa8b1_d974_329e_b1b6_e14b4cf7232b_TB6026_11.jpg)
![<strong>Determine whether the statement is true or false. If it is true, explain why it is true. If it is false, give an example to show why it is false. If h(x, y) = f(x)g(y), where f is continuous on [a, b] and g is continuous on [c, d], then where </strong> A) From the definition follows , so the statement is true. B) From the definition follows , so the statement is false. C) From the definition follows , so the statement is false.](https://storage.examlex.com/TB6026/11eaa8b1_d974_59af_b1b6_399bcbacf9f5_TB6026_11.jpg) , so the statement is true.
, so the statement is true.B) From the definition follows
![<strong>Determine whether the statement is true or false. If it is true, explain why it is true. If it is false, give an example to show why it is false. If h(x, y) = f(x)g(y), where f is continuous on [a, b] and g is continuous on [c, d], then where </strong> A) From the definition follows , so the statement is true. B) From the definition follows , so the statement is false. C) From the definition follows , so the statement is false.](https://storage.examlex.com/TB6026/11eaa8b1_d974_80c0_b1b6_b1d55a522883_TB6026_11.jpg)
![<strong>Determine whether the statement is true or false. If it is true, explain why it is true. If it is false, give an example to show why it is false. If h(x, y) = f(x)g(y), where f is continuous on [a, b] and g is continuous on [c, d], then where </strong> A) From the definition follows , so the statement is true. B) From the definition follows , so the statement is false. C) From the definition follows , so the statement is false.](https://storage.examlex.com/TB6026/11eaa8b1_d974_80c1_b1b6_73bf039417a5_TB6026_11.jpg)
![<strong>Determine whether the statement is true or false. If it is true, explain why it is true. If it is false, give an example to show why it is false. If h(x, y) = f(x)g(y), where f is continuous on [a, b] and g is continuous on [c, d], then where </strong> A) From the definition follows , so the statement is true. B) From the definition follows , so the statement is false. C) From the definition follows , so the statement is false.](https://storage.examlex.com/TB6026/11eaa8b1_d974_a7d2_b1b6_15c2ba687213_TB6026_11.jpg)
![<strong>Determine whether the statement is true or false. If it is true, explain why it is true. If it is false, give an example to show why it is false. If h(x, y) = f(x)g(y), where f is continuous on [a, b] and g is continuous on [c, d], then where </strong> A) From the definition follows , so the statement is true. B) From the definition follows , so the statement is false. C) From the definition follows , so the statement is false.](https://storage.examlex.com/TB6026/11eaa8b1_d974_a7d3_b1b6_5d27e7597df5_TB6026_11.jpg)
![<strong>Determine whether the statement is true or false. If it is true, explain why it is true. If it is false, give an example to show why it is false. If h(x, y) = f(x)g(y), where f is continuous on [a, b] and g is continuous on [c, d], then where </strong> A) From the definition follows , so the statement is true. B) From the definition follows , so the statement is false. C) From the definition follows , so the statement is false.](https://storage.examlex.com/TB6026/11eaa8b1_d974_cee4_b1b6_47cf4c44e522_TB6026_11.jpg) , so the statement is false.
, so the statement is false.C) From the definition follows
![<strong>Determine whether the statement is true or false. If it is true, explain why it is true. If it is false, give an example to show why it is false. If h(x, y) = f(x)g(y), where f is continuous on [a, b] and g is continuous on [c, d], then where </strong> A) From the definition follows , so the statement is true. B) From the definition follows , so the statement is false. C) From the definition follows , so the statement is false.](https://storage.examlex.com/TB6026/11eaa8b1_d974_f5f5_b1b6_95e64b3a9da5_TB6026_11.jpg)
![<strong>Determine whether the statement is true or false. If it is true, explain why it is true. If it is false, give an example to show why it is false. If h(x, y) = f(x)g(y), where f is continuous on [a, b] and g is continuous on [c, d], then where </strong> A) From the definition follows , so the statement is true. B) From the definition follows , so the statement is false. C) From the definition follows , so the statement is false.](https://storage.examlex.com/TB6026/11eaa8b1_d975_1d06_b1b6_cb2ce721719e_TB6026_11.jpg)
![<strong>Determine whether the statement is true or false. If it is true, explain why it is true. If it is false, give an example to show why it is false. If h(x, y) = f(x)g(y), where f is continuous on [a, b] and g is continuous on [c, d], then where </strong> A) From the definition follows , so the statement is true. B) From the definition follows , so the statement is false. C) From the definition follows , so the statement is false.](https://storage.examlex.com/TB6026/11eaa8b1_d975_1d07_b1b6_f91325f40d4a_TB6026_11.jpg)
![<strong>Determine whether the statement is true or false. If it is true, explain why it is true. If it is false, give an example to show why it is false. If h(x, y) = f(x)g(y), where f is continuous on [a, b] and g is continuous on [c, d], then where </strong> A) From the definition follows , so the statement is true. B) From the definition follows , so the statement is false. C) From the definition follows , so the statement is false.](https://storage.examlex.com/TB6026/11eaa8b1_d975_4418_b1b6_75554aad7fa0_TB6026_11.jpg)
![<strong>Determine whether the statement is true or false. If it is true, explain why it is true. If it is false, give an example to show why it is false. If h(x, y) = f(x)g(y), where f is continuous on [a, b] and g is continuous on [c, d], then where </strong> A) From the definition follows , so the statement is true. B) From the definition follows , so the statement is false. C) From the definition follows , so the statement is false.](https://storage.examlex.com/TB6026/11eaa8b1_d975_4419_b1b6_01cc3848185a_TB6026_11.jpg) , so the statement is false.
, so the statement is false.
Unlock Deck
Unlock for access to all 206 flashcards in this deck.
Unlock Deck
k this deck
37
Evaluate the double integral 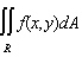 for the function
for the function 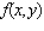 and the region R.
and the region R. 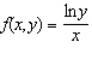 and R is the rectangle defined by
and R is the rectangle defined by 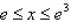 and
and 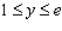 .
.
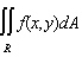 for the function
for the function 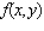 and the region R.
and the region R. 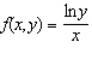 and R is the rectangle defined by
and R is the rectangle defined by 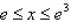 and
and 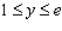 .
.
Unlock Deck
Unlock for access to all 206 flashcards in this deck.
Unlock Deck
k this deck
38
The Country Workshop's total weekly profit (in dollars) realized in manufacturing and selling its rolltop desks is given by the profit function 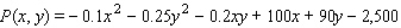 where
where 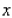 stands for the number of finished units and
stands for the number of finished units and 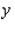 stands for the number of unfinished units manufactured and sold each week. Find the average weekly profit if the number of finished units manufactured and sold varies between
stands for the number of unfinished units manufactured and sold each week. Find the average weekly profit if the number of finished units manufactured and sold varies between 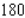 and
and 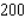 and the number of unfinished units varies between
and the number of unfinished units varies between 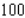 and
and 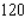 per week. Please round your answer to the nearest dollar, if necessary.
per week. Please round your answer to the nearest dollar, if necessary.
A)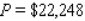 per week
per week
B)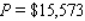 per week
per week
C)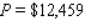 per week
per week
D)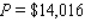 per week
per week
E)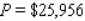 per week
per week
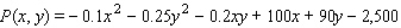 where
where 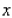 stands for the number of finished units and
stands for the number of finished units and 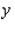 stands for the number of unfinished units manufactured and sold each week. Find the average weekly profit if the number of finished units manufactured and sold varies between
stands for the number of unfinished units manufactured and sold each week. Find the average weekly profit if the number of finished units manufactured and sold varies between 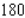 and
and 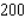 and the number of unfinished units varies between
and the number of unfinished units varies between 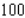 and
and 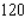 per week. Please round your answer to the nearest dollar, if necessary.
per week. Please round your answer to the nearest dollar, if necessary.A)
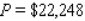 per week
per weekB)
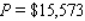 per week
per weekC)
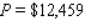 per week
per weekD)
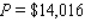 per week
per weekE)
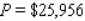 per week
per week
Unlock Deck
Unlock for access to all 206 flashcards in this deck.
Unlock Deck
k this deck
39
Find the volume of the solid bounded above by the surface 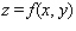 and below by the plane region
and below by the plane region 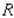 .
. 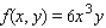 and
and 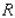 is the region bounded by the graphs of
is the region bounded by the graphs of 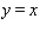 and
and 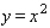 .
.
A)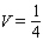
B)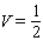
C)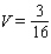
D)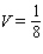
E)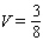
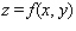 and below by the plane region
and below by the plane region 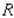 .
. 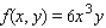 and
and 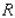 is the region bounded by the graphs of
is the region bounded by the graphs of 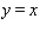 and
and 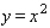 .
.A)
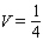
B)
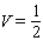
C)
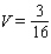
D)
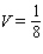
E)
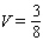

Unlock Deck
Unlock for access to all 206 flashcards in this deck.
Unlock Deck
k this deck
40
Evaluate the double integral 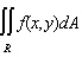 for the given function f(x, y) and the region R.
for the given function f(x, y) and the region R. 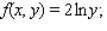 R is the rectangle defined by
R is the rectangle defined by 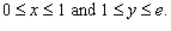
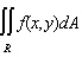 for the given function f(x, y) and the region R.
for the given function f(x, y) and the region R. 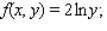 R is the rectangle defined by
R is the rectangle defined by 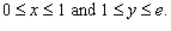

Unlock Deck
Unlock for access to all 206 flashcards in this deck.
Unlock Deck
k this deck
41
Minimize the function 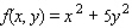 subject to the constraint
subject to the constraint 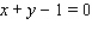 .
.
A)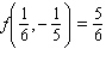
B)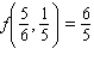
C)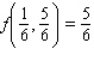
D)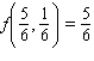
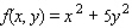 subject to the constraint
subject to the constraint 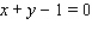 .
.A)
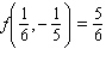
B)
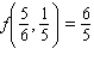
C)
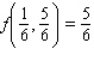
D)
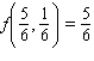

Unlock Deck
Unlock for access to all 206 flashcards in this deck.
Unlock Deck
k this deck
42
Evaluate the double integral 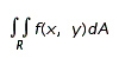 for the given function f(x, y) and the region R.
for the given function f(x, y) and the region R. 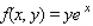 ; R is bounded by
; R is bounded by 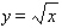 and y = x.
and y = x.
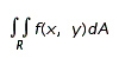 for the given function f(x, y) and the region R.
for the given function f(x, y) and the region R. 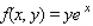 ; R is bounded by
; R is bounded by 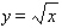 and y = x.
and y = x.
Unlock Deck
Unlock for access to all 206 flashcards in this deck.
Unlock Deck
k this deck
43
Minimize the function 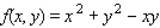 subject to the constraint
subject to the constraint 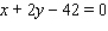 .
.
A)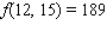
B)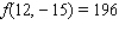
C)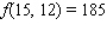
D)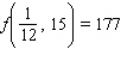
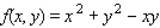 subject to the constraint
subject to the constraint 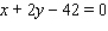 .
.A)
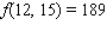
B)
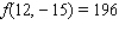
C)
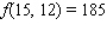
D)
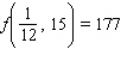

Unlock Deck
Unlock for access to all 206 flashcards in this deck.
Unlock Deck
k this deck
44
Maximize the function 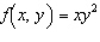 subject to the constraints
subject to the constraints 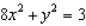 .
.
A) Max. of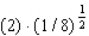 at
at
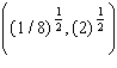
B) Max. of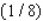 at
at
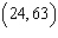
C) Max. of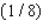 at
at
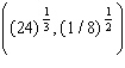
D) Max. of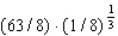 at
at
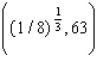
E) Max. of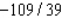 at
at
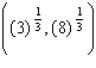
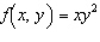 subject to the constraints
subject to the constraints 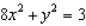 .
.A) Max. of
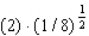 at
at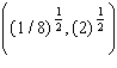
B) Max. of
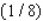 at
at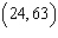
C) Max. of
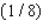 at
at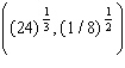
D) Max. of
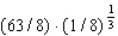 at
at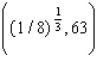
E) Max. of
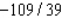 at
at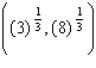

Unlock Deck
Unlock for access to all 206 flashcards in this deck.
Unlock Deck
k this deck
45
Maximize the function 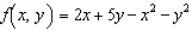 subject to the constraints
subject to the constraints 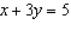 .
.
A) Max. of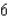 at
at
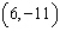
B) Max. of -2 at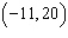
C) Max. of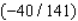 at
at
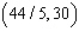
D) Max. of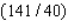 at
at
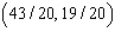
E) Max. of 6 at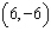
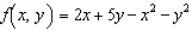 subject to the constraints
subject to the constraints 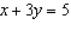 .
.A) Max. of
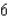 at
at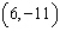
B) Max. of -2 at
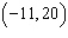
C) Max. of
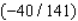 at
at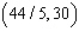
D) Max. of
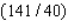 at
at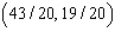
E) Max. of 6 at
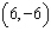

Unlock Deck
Unlock for access to all 206 flashcards in this deck.
Unlock Deck
k this deck
46
Minimize the function 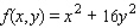 subject to the constraint
subject to the constraint 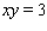 .
.
A)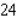
B)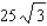
C)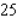
D)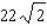
E)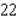
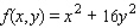 subject to the constraint
subject to the constraint 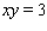 .
.A)
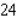
B)
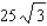
C)
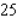
D)
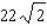
E)
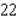

Unlock Deck
Unlock for access to all 206 flashcards in this deck.
Unlock Deck
k this deck
47
Find the volume of the solid bounded above by the surface
z = f(x, y)
and below by the plane region R.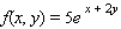 ; R is the triangle with vertices (0, 0), (5, 0) and (0, 5).
; R is the triangle with vertices (0, 0), (5, 0) and (0, 5).
z = f(x, y)
and below by the plane region R.
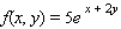 ; R is the triangle with vertices (0, 0), (5, 0) and (0, 5).
; R is the triangle with vertices (0, 0), (5, 0) and (0, 5).
Unlock Deck
Unlock for access to all 206 flashcards in this deck.
Unlock Deck
k this deck
48
Find the average value of the given function
f(x, y)
over the plane region R.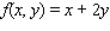 ; R is the triangle with vertices (0, 0), (2, 0) and (2, 2).
; R is the triangle with vertices (0, 0), (2, 0) and (2, 2).
f(x, y)
over the plane region R.
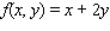 ; R is the triangle with vertices (0, 0), (2, 0) and (2, 2).
; R is the triangle with vertices (0, 0), (2, 0) and (2, 2).
Unlock Deck
Unlock for access to all 206 flashcards in this deck.
Unlock Deck
k this deck
49
Maximize the function 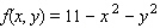 subject to the constraint
subject to the constraint 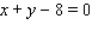 .
.
A)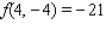
B)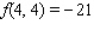
C)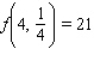
D)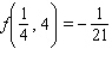
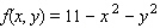 subject to the constraint
subject to the constraint 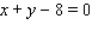 .
.A)
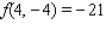
B)
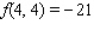
C)
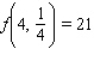
D)
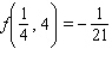

Unlock Deck
Unlock for access to all 206 flashcards in this deck.
Unlock Deck
k this deck
50
Maximize the function 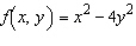 subject to the constraints
subject to the constraints 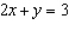 .
.
A) Max. of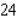 at
at
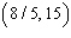
B) Max. of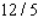 at
at
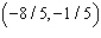
C) Max. of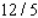 at
at
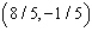
D) Max. of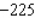 at
at
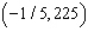
E) Max. of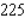 at
at
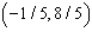
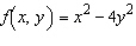 subject to the constraints
subject to the constraints 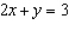 .
.A) Max. of
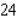 at
at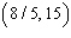
B) Max. of
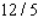 at
at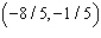
C) Max. of
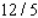 at
at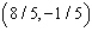
D) Max. of
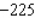 at
at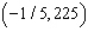
E) Max. of
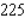 at
at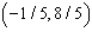

Unlock Deck
Unlock for access to all 206 flashcards in this deck.
Unlock Deck
k this deck
51
The population density of a certain city is given by the function 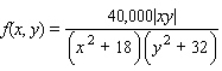 where the origin (0, 0) gives the location of the government center. Find the population inside the rectangular area described by
where the origin (0, 0) gives the location of the government center. Find the population inside the rectangular area described by 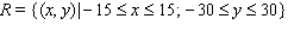
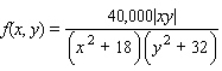 where the origin (0, 0) gives the location of the government center. Find the population inside the rectangular area described by
where the origin (0, 0) gives the location of the government center. Find the population inside the rectangular area described by 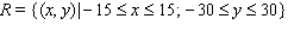

Unlock Deck
Unlock for access to all 206 flashcards in this deck.
Unlock Deck
k this deck
52
Find the average value of the function 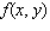 over the plane region
over the plane region  .
. 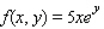 and
and  is the triangle with vertices
is the triangle with vertices 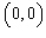 ,
, 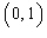 and
and 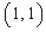 .
.
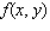 over the plane region
over the plane region 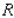 .
. 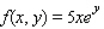 and
and  is the triangle with vertices
is the triangle with vertices 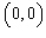 ,
, 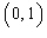 and
and 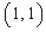 .
.
Unlock Deck
Unlock for access to all 206 flashcards in this deck.
Unlock Deck
k this deck
53
Find the volume of the solid bounded above by the surface
z = f(x, y)
and below by the plane region R.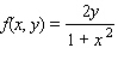 ; R is the region bounded by
; R is the region bounded by 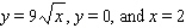 .
.
z = f(x, y)
and below by the plane region R.
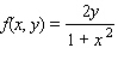 ; R is the region bounded by
; R is the region bounded by 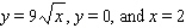 .
.
Unlock Deck
Unlock for access to all 206 flashcards in this deck.
Unlock Deck
k this deck
54
Find the average value of the given function
f(x, y)
over the plane region R.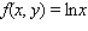 ; R is the region bounded by the graph of y = 6x and y = 0 from x = 1 to x = 5.
; R is the region bounded by the graph of y = 6x and y = 0 from x = 1 to x = 5.
f(x, y)
over the plane region R.
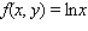 ; R is the region bounded by the graph of y = 6x and y = 0 from x = 1 to x = 5.
; R is the region bounded by the graph of y = 6x and y = 0 from x = 1 to x = 5.
Unlock Deck
Unlock for access to all 206 flashcards in this deck.
Unlock Deck
k this deck
55
Maximize the function 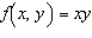 subject to the constraints
subject to the constraints 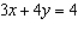 .
.
A) Max. of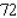 at
at
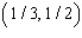
B) Max. of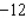 at
at
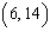
C) Max. of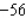 at
at
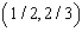
D) Max. of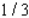 at
at
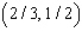
E) Max. of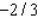 at
at
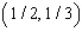
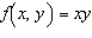 subject to the constraints
subject to the constraints 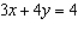 .
.A) Max. of
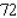 at
at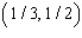
B) Max. of
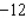 at
at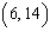
C) Max. of
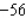 at
at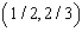
D) Max. of
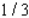 at
at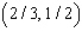
E) Max. of
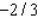 at
at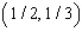

Unlock Deck
Unlock for access to all 206 flashcards in this deck.
Unlock Deck
k this deck
56
Minimize the function 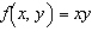 subject to the constraints
subject to the constraints 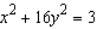
A) Min. of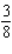 at
at
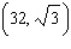
B) Min. of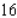 at
at
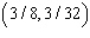
C) Min. of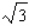 at
at
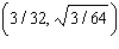
D) Min. of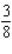 at
at
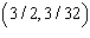
E) Min. of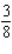 at
at
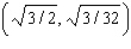
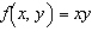 subject to the constraints
subject to the constraints 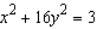
A) Min. of
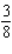 at
at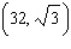
B) Min. of
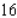 at
at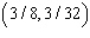
C) Min. of
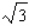 at
at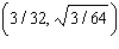
D) Min. of
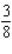 at
at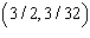
E) Min. of
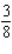 at
at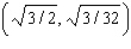

Unlock Deck
Unlock for access to all 206 flashcards in this deck.
Unlock Deck
k this deck
57
Use a double integral to find the volume of the solid shown in the figure. 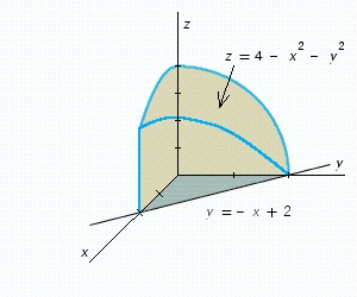


Unlock Deck
Unlock for access to all 206 flashcards in this deck.
Unlock Deck
k this deck
58
Determine whether the statement is true or false. If it is true, explain why it is true. If it is false, give an example to show why it is false.
If h(x, y) = f(x)g(y), where f is continuous on [a, b] and g is continuous on [c, d], then![Determine whether the statement is true or false. If it is true, explain why it is true. If it is false, give an example to show why it is false. If h(x, y) = f(x)g(y), where f is continuous on [a, b] and g is continuous on [c, d], then where](https://storage.examlex.com/TB6026/11eaa8b1_d981_786c_b1b6_f3f19210a87b_TB6026_11.jpg) where
where ![Determine whether the statement is true or false. If it is true, explain why it is true. If it is false, give an example to show why it is false. If h(x, y) = f(x)g(y), where f is continuous on [a, b] and g is continuous on [c, d], then where](https://storage.examlex.com/TB6026/11eaa8b1_d981_786d_b1b6_296c145eb06d_TB6026_11.jpg)
If h(x, y) = f(x)g(y), where f is continuous on [a, b] and g is continuous on [c, d], then
![Determine whether the statement is true or false. If it is true, explain why it is true. If it is false, give an example to show why it is false. If h(x, y) = f(x)g(y), where f is continuous on [a, b] and g is continuous on [c, d], then where](https://storage.examlex.com/TB6026/11eaa8b1_d981_786c_b1b6_f3f19210a87b_TB6026_11.jpg) where
where ![Determine whether the statement is true or false. If it is true, explain why it is true. If it is false, give an example to show why it is false. If h(x, y) = f(x)g(y), where f is continuous on [a, b] and g is continuous on [c, d], then where](https://storage.examlex.com/TB6026/11eaa8b1_d981_786d_b1b6_296c145eb06d_TB6026_11.jpg)

Unlock Deck
Unlock for access to all 206 flashcards in this deck.
Unlock Deck
k this deck
59
Find the volume of the solid bounded above by the surface 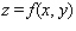 and below by the plane region
and below by the plane region 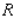 .
. 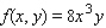 and
and 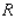 is the region bounded by the graphs of
is the region bounded by the graphs of 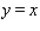 and
and 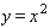 .
.
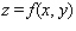 and below by the plane region
and below by the plane region 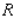 .
. 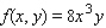 and
and 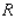 is the region bounded by the graphs of
is the region bounded by the graphs of 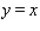 and
and 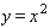 .
.
Unlock Deck
Unlock for access to all 206 flashcards in this deck.
Unlock Deck
k this deck
60
Use a double integral to find the volume of the solid shown in the figure. 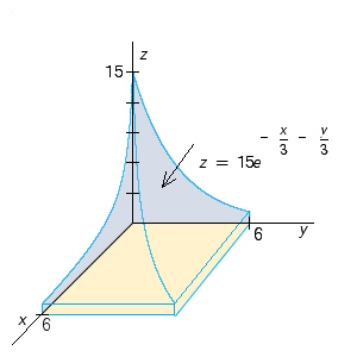


Unlock Deck
Unlock for access to all 206 flashcards in this deck.
Unlock Deck
k this deck
61
Minimize the function 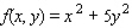 subject to the constraint
subject to the constraint 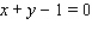 .
.
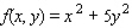 subject to the constraint
subject to the constraint 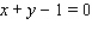 .
.
Unlock Deck
Unlock for access to all 206 flashcards in this deck.
Unlock Deck
k this deck
62
The total weekly profit (in dollars) realized by Country Workshop in manufacturing and selling its rolltop desks is given by the profit function 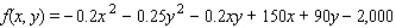 where x stands for the number of finished units and y denotes the number of unfinished units manufactured and sold each week. The company's management decides to restrict the manufacture of these desks to a total of exactly 100 units/week. How many finished and how many unfinished units should be manufactured each week to maximize the company's weekly profit?
where x stands for the number of finished units and y denotes the number of unfinished units manufactured and sold each week. The company's management decides to restrict the manufacture of these desks to a total of exactly 100 units/week. How many finished and how many unfinished units should be manufactured each week to maximize the company's weekly profit?
A) 80 finished and 20 unfinished units
B) 70 finished and 30 unfinished units
C) 60 finished and 40 unfinished units
D) 110 finished and -10 unfinished units
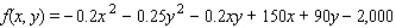 where x stands for the number of finished units and y denotes the number of unfinished units manufactured and sold each week. The company's management decides to restrict the manufacture of these desks to a total of exactly 100 units/week. How many finished and how many unfinished units should be manufactured each week to maximize the company's weekly profit?
where x stands for the number of finished units and y denotes the number of unfinished units manufactured and sold each week. The company's management decides to restrict the manufacture of these desks to a total of exactly 100 units/week. How many finished and how many unfinished units should be manufactured each week to maximize the company's weekly profit?A) 80 finished and 20 unfinished units
B) 70 finished and 30 unfinished units
C) 60 finished and 40 unfinished units
D) 110 finished and -10 unfinished units

Unlock Deck
Unlock for access to all 206 flashcards in this deck.
Unlock Deck
k this deck
63
The management of UNICO Department Store decides to enclose an 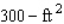 area outside their building to display potted plants. The enclosed area will be a rectangle, one side of which is provided by the external walls of the store. Two sides of the enclosure will be made of pine board, and the fourth side will be made of galvanized steel fencing material. If the pine board fencing costs $9/running foot and the steel fencing costs $3/running foot, determine the dimensions of the enclosure that will cost the least to erect. Round your answers to two decimal places.
area outside their building to display potted plants. The enclosed area will be a rectangle, one side of which is provided by the external walls of the store. Two sides of the enclosure will be made of pine board, and the fourth side will be made of galvanized steel fencing material. If the pine board fencing costs $9/running foot and the steel fencing costs $3/running foot, determine the dimensions of the enclosure that will cost the least to erect. Round your answers to two decimal places. 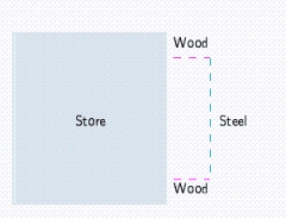
A) 7.07 ft by 42.43 ft
B) 8.61 ft by 40.89 ft
C) 5.06 ft by 44.44 ft
D) 7.24 ft by 42.26 ft
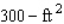 area outside their building to display potted plants. The enclosed area will be a rectangle, one side of which is provided by the external walls of the store. Two sides of the enclosure will be made of pine board, and the fourth side will be made of galvanized steel fencing material. If the pine board fencing costs $9/running foot and the steel fencing costs $3/running foot, determine the dimensions of the enclosure that will cost the least to erect. Round your answers to two decimal places.
area outside their building to display potted plants. The enclosed area will be a rectangle, one side of which is provided by the external walls of the store. Two sides of the enclosure will be made of pine board, and the fourth side will be made of galvanized steel fencing material. If the pine board fencing costs $9/running foot and the steel fencing costs $3/running foot, determine the dimensions of the enclosure that will cost the least to erect. Round your answers to two decimal places. 
A) 7.07 ft by 42.43 ft
B) 8.61 ft by 40.89 ft
C) 5.06 ft by 44.44 ft
D) 7.24 ft by 42.26 ft

Unlock Deck
Unlock for access to all 206 flashcards in this deck.
Unlock Deck
k this deck
64
Maximize the function 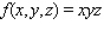 subject to the constraint
subject to the constraint 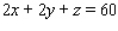 .
.
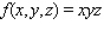 subject to the constraint
subject to the constraint 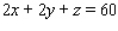 .
.
Unlock Deck
Unlock for access to all 206 flashcards in this deck.
Unlock Deck
k this deck
65
Minimize the function 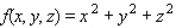 subject to the constraint
subject to the constraint 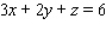 .
.
A)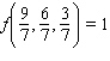
B)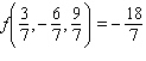
C)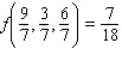
D)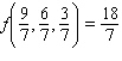
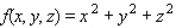 subject to the constraint
subject to the constraint 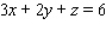 .
.A)
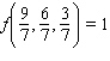
B)
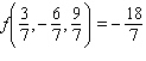
C)
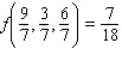
D)
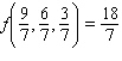

Unlock Deck
Unlock for access to all 206 flashcards in this deck.
Unlock Deck
k this deck
66
Find the maximum and minimum values of the function 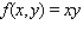 subject to the constraint
subject to the constraint 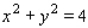 .
.
A)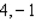
B)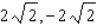
C)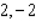
D)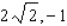
E)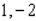
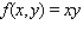 subject to the constraint
subject to the constraint 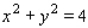 .
.A)
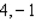
B)
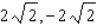
C)
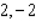
D)
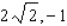
E)
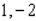

Unlock Deck
Unlock for access to all 206 flashcards in this deck.
Unlock Deck
k this deck
67
Maximize the function 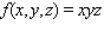 subject to the constraint
subject to the constraint 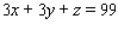 .
.
A)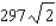
B)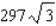
C)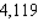
D)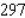
E)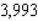
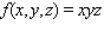 subject to the constraint
subject to the constraint 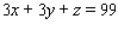 .
.A)
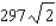
B)
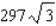
C)
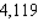
D)
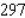
E)
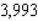

Unlock Deck
Unlock for access to all 206 flashcards in this deck.
Unlock Deck
k this deck
68
Maximize the function 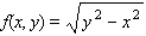 subject to the constraint
subject to the constraint 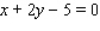 .
.
A)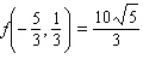
B)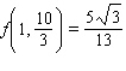
C)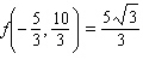
D)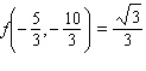
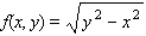 subject to the constraint
subject to the constraint 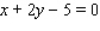 .
.A)
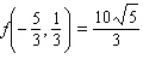
B)
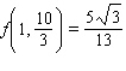
C)
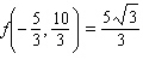
D)
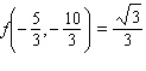

Unlock Deck
Unlock for access to all 206 flashcards in this deck.
Unlock Deck
k this deck
69
Find the maximum and minimum values of the function 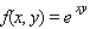 subject to the constraint
subject to the constraint 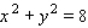 .
.
A) Maxima :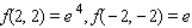 Minima :
Minima :
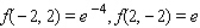
B) Maxima :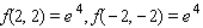 Minima :
Minima :
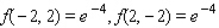
C) Maxima :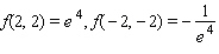 Minima :
Minima :
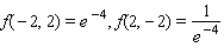
D) Maxima :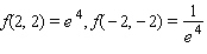 Minima :
Minima :
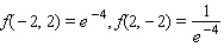
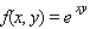 subject to the constraint
subject to the constraint 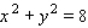 .
.A) Maxima :
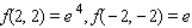 Minima :
Minima :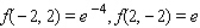
B) Maxima :
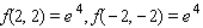 Minima :
Minima :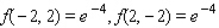
C) Maxima :
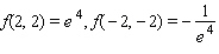 Minima :
Minima :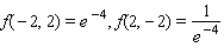
D) Maxima :
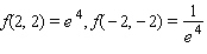 Minima :
Minima :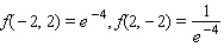

Unlock Deck
Unlock for access to all 206 flashcards in this deck.
Unlock Deck
k this deck
70
Determine whether the statement is true or false. If it is true, explain why it is true. If it is false, give an example to show why it is false. If 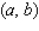 gives rise to a (constrained) relative extremum of
gives rise to a (constrained) relative extremum of 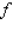 subject to the constraint
subject to the constraint 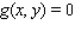 , then ,
, then , 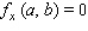 and
and 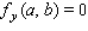 , simultaneously.
, simultaneously.
A) Let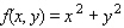 and
and
 , then the point
, then the point
 gives rise to a (constrained) relative extremum(minimum),
gives rise to a (constrained) relative extremum(minimum),
 and
and
 , so the statement is true.
, so the statement is true.
B) Let and
and
 , then the point
, then the point
 gives rise to a (constrained) relative extremum(minimum),
gives rise to a (constrained) relative extremum(minimum),
 and
and
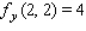 , so the statement is false.
, so the statement is false.
 gives rise to a (constrained) relative extremum of
gives rise to a (constrained) relative extremum of  subject to the constraint
subject to the constraint 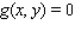 , then ,
, then , 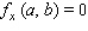 and
and 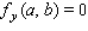 , simultaneously.
, simultaneously.A) Let
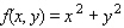 and
and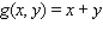 , then the point
, then the point gives rise to a (constrained) relative extremum(minimum),
gives rise to a (constrained) relative extremum(minimum), and
and , so the statement is true.
, so the statement is true.B) Let
 and
and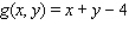 , then the point
, then the point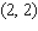 gives rise to a (constrained) relative extremum(minimum),
gives rise to a (constrained) relative extremum(minimum),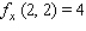 and
and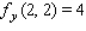 , so the statement is false.
, so the statement is false.
Unlock Deck
Unlock for access to all 206 flashcards in this deck.
Unlock Deck
k this deck
71
The total daily profit (in dollars) realized by Weston Publishing in publishing and selling its dictionaries is given by the profit function 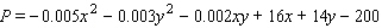 where x stands for the number of deluxe editions and y denotes the number of standard editions sold daily. Weston's management decides that publication of these dictionaries should be restricted to a total of exactly 700 copies/day. How many deluxe copies and how many standard copies should be published each day to maximize Weston's daily profit?
where x stands for the number of deluxe editions and y denotes the number of standard editions sold daily. Weston's management decides that publication of these dictionaries should be restricted to a total of exactly 700 copies/day. How many deluxe copies and how many standard copies should be published each day to maximize Weston's daily profit?
A) 320 deluxe copies, 330 standard copies
B) 450 deluxe copies, 240 standard copies
C) 320 deluxe copies, 300 standard copies
D) 450 deluxe copies, 330 standard copies
E) 400 deluxe copies, 300 standard copies
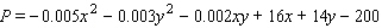 where x stands for the number of deluxe editions and y denotes the number of standard editions sold daily. Weston's management decides that publication of these dictionaries should be restricted to a total of exactly 700 copies/day. How many deluxe copies and how many standard copies should be published each day to maximize Weston's daily profit?
where x stands for the number of deluxe editions and y denotes the number of standard editions sold daily. Weston's management decides that publication of these dictionaries should be restricted to a total of exactly 700 copies/day. How many deluxe copies and how many standard copies should be published each day to maximize Weston's daily profit?A) 320 deluxe copies, 330 standard copies
B) 450 deluxe copies, 240 standard copies
C) 320 deluxe copies, 300 standard copies
D) 450 deluxe copies, 330 standard copies
E) 400 deluxe copies, 300 standard copies

Unlock Deck
Unlock for access to all 206 flashcards in this deck.
Unlock Deck
k this deck
72
A building in the shape of a rectangular box is to have a volume of 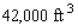 (see the figure). It is estimated that the annual heating and cooling costs will be $2/square foot for the top, $7/square foot for the front and back, and $6/square foot for the sides. Find the dimensions of the building that will result in a minimal annual heating and cooling cost. What is the minimal annual heating and cooling cost(C)?
(see the figure). It is estimated that the annual heating and cooling costs will be $2/square foot for the top, $7/square foot for the front and back, and $6/square foot for the sides. Find the dimensions of the building that will result in a minimal annual heating and cooling cost. What is the minimal annual heating and cooling cost(C)? 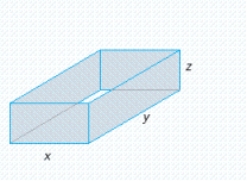
A)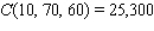
B)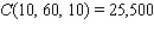
C)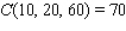
D)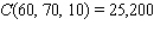
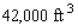 (see the figure). It is estimated that the annual heating and cooling costs will be $2/square foot for the top, $7/square foot for the front and back, and $6/square foot for the sides. Find the dimensions of the building that will result in a minimal annual heating and cooling cost. What is the minimal annual heating and cooling cost(C)?
(see the figure). It is estimated that the annual heating and cooling costs will be $2/square foot for the top, $7/square foot for the front and back, and $6/square foot for the sides. Find the dimensions of the building that will result in a minimal annual heating and cooling cost. What is the minimal annual heating and cooling cost(C)? 
A)
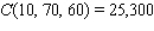
B)
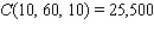
C)
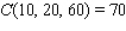
D)
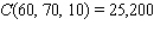

Unlock Deck
Unlock for access to all 206 flashcards in this deck.
Unlock Deck
k this deck
73
An open rectangular box is to be constructed from material that costs 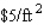 for the bottom and
for the bottom and 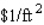 for its sides. Find the dimensions of the box of greatest volume that can be constructed for
for its sides. Find the dimensions of the box of greatest volume that can be constructed for 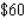 .
.
A)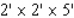
B)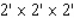
C)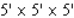
D)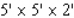
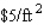 for the bottom and
for the bottom and 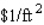 for its sides. Find the dimensions of the box of greatest volume that can be constructed for
for its sides. Find the dimensions of the box of greatest volume that can be constructed for 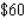 .
.A)
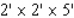
B)
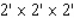
C)
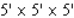
D)
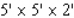

Unlock Deck
Unlock for access to all 206 flashcards in this deck.
Unlock Deck
k this deck
74
The Ross-Simons Company has a monthly advertising budget of $40,000. Their marketing department estimates that if they spend x dollars on newspaper advertising and y dollars on television advertising, then the monthly sales will be given by 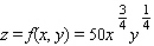 dollars. Determine how much money Ross-Simons should spend on newspaper ads and on television ads each month to maximize its monthly sales.
dollars. Determine how much money Ross-Simons should spend on newspaper ads and on television ads each month to maximize its monthly sales.
A) $31,000 on newspaper advertisements and $11,000 on television advertisements
B) $28,000 on newspaper advertisements and $8,000 on television advertisements
C) $33,000 on newspaper advertisements and $13,000 on television advertisements
D) $30,000 on newspaper advertisements and $10,000 on television advertisements
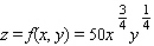 dollars. Determine how much money Ross-Simons should spend on newspaper ads and on television ads each month to maximize its monthly sales.
dollars. Determine how much money Ross-Simons should spend on newspaper ads and on television ads each month to maximize its monthly sales.A) $31,000 on newspaper advertisements and $11,000 on television advertisements
B) $28,000 on newspaper advertisements and $8,000 on television advertisements
C) $33,000 on newspaper advertisements and $13,000 on television advertisements
D) $30,000 on newspaper advertisements and $10,000 on television advertisements

Unlock Deck
Unlock for access to all 206 flashcards in this deck.
Unlock Deck
k this deck
75
A closed rectangular box having a volume of 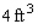 is to be constructed. If the material for the sides costs
is to be constructed. If the material for the sides costs 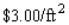 and the material for the top and bottom costs
and the material for the top and bottom costs 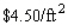 , find the dimensions of the box that can be constructed with minimum cost.
, find the dimensions of the box that can be constructed with minimum cost.
A)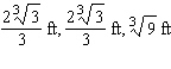
B)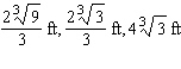
C)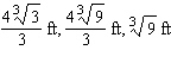
D)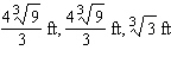
E)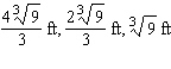
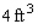 is to be constructed. If the material for the sides costs
is to be constructed. If the material for the sides costs 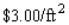 and the material for the top and bottom costs
and the material for the top and bottom costs 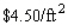 , find the dimensions of the box that can be constructed with minimum cost.
, find the dimensions of the box that can be constructed with minimum cost.A)
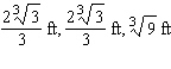
B)
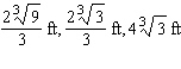
C)
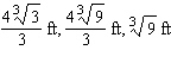
D)
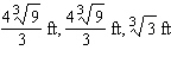
E)
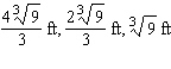

Unlock Deck
Unlock for access to all 206 flashcards in this deck.
Unlock Deck
k this deck
76
Minimize the function 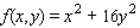 subject to the constraint
subject to the constraint 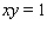 .
.
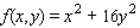 subject to the constraint
subject to the constraint 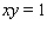 .
.
Unlock Deck
Unlock for access to all 206 flashcards in this deck.
Unlock Deck
k this deck
77
John Mills- the propietor of Mills Engine Company, a manufacturer of mdel airplane engine-finds that it takes 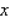 units of labor and
units of labor and 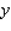 units of capital to produce
units of capital to produce 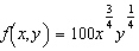 units of the product. If a unit of labor costs
units of the product. If a unit of labor costs 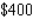 , a unit of capital costs
, a unit of capital costs 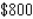 and
and 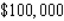 is bugeted for production, determine how long units should be expended on on labour and how many units should be expended on capital in order to maximize production.
is bugeted for production, determine how long units should be expended on on labour and how many units should be expended on capital in order to maximize production.
A)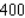 units of labour and
units of labour and
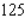 units of capital.
units of capital.
B)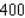 units of labour and
units of labour and
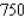 units of capital.
units of capital.
C)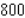 units of labour and
units of labour and
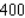 units of capital.
units of capital.
D)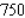 units of labour and
units of labour and
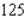 units of capital.
units of capital.
E)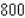 units of labour and
units of labour and
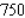 units of capital.
units of capital.
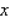 units of labor and
units of labor and 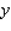 units of capital to produce
units of capital to produce 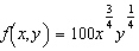 units of the product. If a unit of labor costs
units of the product. If a unit of labor costs 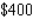 , a unit of capital costs
, a unit of capital costs 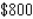 and
and 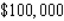 is bugeted for production, determine how long units should be expended on on labour and how many units should be expended on capital in order to maximize production.
is bugeted for production, determine how long units should be expended on on labour and how many units should be expended on capital in order to maximize production.A)
 units of labour and
units of labour and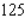 units of capital.
units of capital.B)
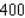 units of labour and
units of labour and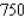 units of capital.
units of capital.C)
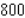 units of labour and
units of labour and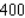 units of capital.
units of capital.D)
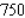 units of labour and
units of labour and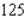 units of capital.
units of capital.E)
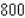 units of labour and
units of labour and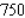 units of capital.
units of capital.
Unlock Deck
Unlock for access to all 206 flashcards in this deck.
Unlock Deck
k this deck
78
Find the maximum and minimum values of the function 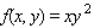 subject to the constraint
subject to the constraint 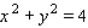 .
.
A) Maxima :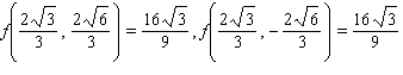 Minima :
Minima :
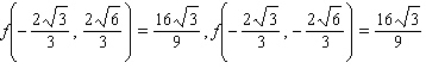
B) Maxima :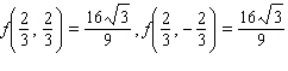 Minima :
Minima :
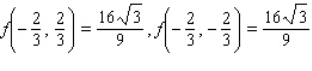
C) Maxima :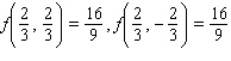 Minima :
Minima :
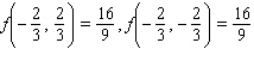
D) Maxima :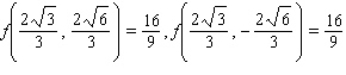 Minima :
Minima :
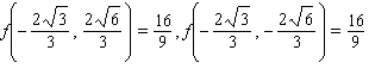
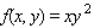 subject to the constraint
subject to the constraint 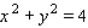 .
.A) Maxima :
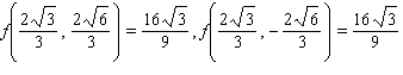 Minima :
Minima :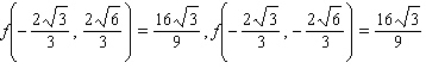
B) Maxima :
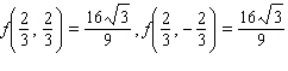 Minima :
Minima :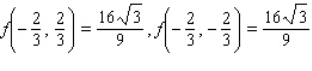
C) Maxima :
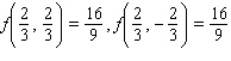 Minima :
Minima :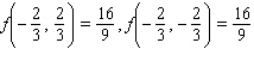
D) Maxima :
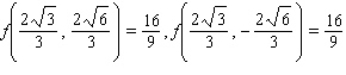 Minima :
Minima :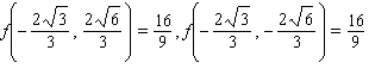

Unlock Deck
Unlock for access to all 206 flashcards in this deck.
Unlock Deck
k this deck
79
The Company requires that its corned beef hash containers have a capacity of 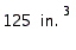 , be right circular cylinders, and be made of a tin alloy. Find the radius and height of the least expensive container that can be made if the metal for the side and bottom costs
, be right circular cylinders, and be made of a tin alloy. Find the radius and height of the least expensive container that can be made if the metal for the side and bottom costs  and the metal for the pull-off lid costs
and the metal for the pull-off lid costs  .
.
A)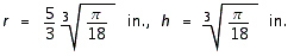
B)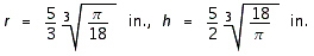
C)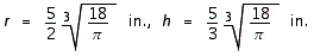
D)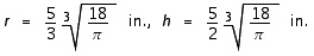
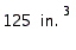 , be right circular cylinders, and be made of a tin alloy. Find the radius and height of the least expensive container that can be made if the metal for the side and bottom costs
, be right circular cylinders, and be made of a tin alloy. Find the radius and height of the least expensive container that can be made if the metal for the side and bottom costs  and the metal for the pull-off lid costs
and the metal for the pull-off lid costs  .
.A)
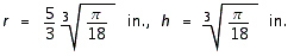
B)
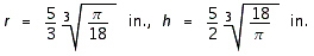
C)
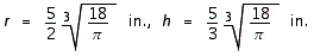
D)
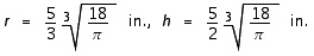

Unlock Deck
Unlock for access to all 206 flashcards in this deck.
Unlock Deck
k this deck
80
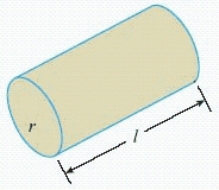
Postal regulations specify that a parcel sent by parcel post may have a combined length and girth of no more than 105 in. Find the dimensions of the cylindrical package of greatest volume that may be sent through the mail. What is the volume of such a package? Hint: The length plus the girth is 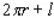 , and the volume is
, and the volume is 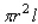 .
. 
A)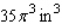
B)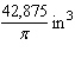
C)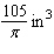
D)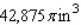
E)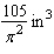
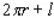 , and the volume is
, and the volume is 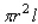 .
. 
A)
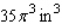
B)
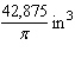
C)
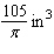
D)
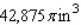
E)
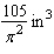

Unlock Deck
Unlock for access to all 206 flashcards in this deck.
Unlock Deck
k this deck


