Deck 14: Analysis of Variance
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/125
Play
Full screen (f)
Deck 14: Analysis of Variance
1
The within-treatments variation provides a measure of the amount of variation in the response variables that is caused by the treatments.
False
2
The distribution of the test statistic for analysis of variance is the F-distribution.
True
3
In one-way ANOVA, the total variation SS(Total) is partitioned into two sources of variation: the sum of squares for treatments (SST) and the sum of squares for error (SSE).
True
4
The sum of squares for treatments (SST) is the variation attributed to the differences between the treatment means, while the sum of squares for error (SSE) measures the within-treatment variation.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
5
The sum of squares for error is also known as the between-treatments variation.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
6
When the F-test is used for ANOVA, the rejection region is always in the right tail.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
7
The sum of squares for treatments, SST, achieves its smallest value (zero) when all the sample means are equal.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
8
The analysis of variance (ANOVA) tests hypotheses about population variances and requires all the population means to be equal.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
9
If the numerator (MST) degrees of freedom is 3 and the denominator (MSE) degrees of freedom is 18, the total number of observations must equal 21.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
10
The F-statistic in a one-way ANOVA represents the variation within the treatments divided by the variation between the treatments.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
11
Conducting t-tests for each pair or population means is statistically equivalent to conducting one F-test comparing all the population means.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
12
In one-way ANOVA, the test statistic is defined as the ratio of the mean square for error (MSE) and the mean square for treatments (MST), namely, F = MSE / MST.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
13
The F-test used in one-way ANOVA is an extension of the t-test of 1 - 2.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
14
The F-test in ANOVA is an expansion of the t-test for two independent population means.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
15
We use the analysis of variance (ANOVA) technique to compare two or more population means.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
16
In ANOVA, a criterion by which the populations are classified is called a factor.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
17
The analysis of variance (ANOVA) technique analyzes the variance of the data to determine whether differences exist between the population means.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
18
The sum of squares for error (SSE) measures the amount of variation that is explained by the ANOVA model, while the sum of squares for treatments (SST) measures the amount of variation that remains unexplained.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
19
The F-test in ANOVA tests whether or not the population variances are equal.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
20
We can use the F-test to determine whether 1 is greater than 2.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
21
The Bonferroni adjustment decreases the experimentwise Type I error rate, but it increases the probability of a Type II error.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
22
A randomized block experiment having five treatments and six blocks produced the following values: SST = 252, SS(Total) = 1,545, SSE = 198. The value of SSB must be 1095.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
23
SSE in the independent samples design is equal to the sum of SSB and SSE in the randomized block design.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
24
In a one-way ANOVA, error variability is computed as the sum of the squared errors, SSE, for all values of the response variable. This variability is the:
A) the total variation.
B) within-treatments variation.
C) between-treatments variation.
D) None of these choices.
A) the total variation.
B) within-treatments variation.
C) between-treatments variation.
D) None of these choices.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
25
Tukey's multiple comparison method is based on the Studentized range statistic.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
26
In a single-factor analysis of variance, MST is the mean square for treatments and MSE is the mean square for error. The null hypothesis of equal population means is rejected if:
A) MST is much larger than MSE.
B) MST is much smaller than MSE.
C) MST is equal to MSE.
D) None of these choices.
A) MST is much larger than MSE.
B) MST is much smaller than MSE.
C) MST is equal to MSE.
D) None of these choices.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
27
The purpose of designing a randomized block experiment is to reduce the between-treatments variation (SST) to more easily detect differences between the treatment means.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
28
The F-test of the randomized block design of the analysis of variance has the same requirements as the independent samples design; that is, the random variable must be normally distributed and the population variances must be equal.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
29
The test statistic of the single-factor ANOVA equals:
A) sum of squares for treatments / sum of squares for error.
B) sum of squares for error / sum of squares for treatments.
C) mean square for treatments / mean square for error.
D) mean square for error / mean square for treatments.
A) sum of squares for treatments / sum of squares for error.
B) sum of squares for error / sum of squares for treatments.
C) mean square for treatments / mean square for error.
D) mean square for error / mean square for treatments.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
30
A randomized block design with 4 treatments and 5 blocks produced the following sum of squares values: SS(Total) = 2000, SST = 400, SSE = 200. The value of MSB must be 350.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
31
When the variation associated with blocks is removed from the data, SSE increases.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
32
In employing the randomized block design, the primary interest lies in reducing sum of squares for blocks (SSB).

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
33
Which of the following is not a required condition for one-way ANOVA?
A) The sample sizes must be equal.
B) The populations must all be normally distributed.
C) The population variances must be equal.
D) The samples for each treatment must be selected randomly and independently.
A) The sample sizes must be equal.
B) The populations must all be normally distributed.
C) The population variances must be equal.
D) The samples for each treatment must be selected randomly and independently.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
34
In one-way ANOVA, the amount of total variation that is unexplained is measured by the:
A) sum of squares for treatments.
B) degrees of freedom.
C) total sum of squares.
D) sum of squares for error.
A) sum of squares for treatments.
B) degrees of freedom.
C) total sum of squares.
D) sum of squares for error.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
35
When the problem objective is to compare more than two populations, the experimental design that is the counterpart of the matched pairs experiment is called the randomized block design.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
36
Tukey's multiple comparison method is more powerful than Fisher's LSD Method at finding differences in pairwise population means.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
37
Fisher's least significant difference method (LSD) substitutes the pooled variance estimator from the equal variances t-test with the MSE from ANOVA.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
38
The Bonferroni adjustment to Fisher's Least Significant Difference (LSD) multiple comparison method is made by dividing the specified experimentwise Type I error rate by the number of pairs of population means.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
39
Multiple comparison methods are used to determine whether or not any differences occur amongst a group of population means.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
40
One example of a blocking variable is the dosage level that each subject is assigned to in a randomized experiment.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
41
In ANOVA, the F-test is the ratio of two sample variances. In the one-way ANOVA (completely randomized design), the variance used as a numerator of the ratio is:
A) mean square for treatments.
B) mean square for error.
C) total sum of squares.
D) None of these choices.
A) mean square for treatments.
B) mean square for error.
C) total sum of squares.
D) None of these choices.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
42
In the one-way ANOVA where there are k treatments and n observations, the degrees of freedom for the F-statistic are equal to, respectively:
A) n and k.
B) k and n.
C) n - k and k - 1.
D) k- 1 and n - k.
A) n and k.
B) k and n.
C) n - k and k - 1.
D) k- 1 and n - k.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
43
One-way ANOVA is applied to independent samples taken from three normally distributed populations with equal variances. Which of the following is the null hypothesis for this procedure?
A) 1 + 2 + 3 = 0
B) 1 + 2 + 3 0
C) 1 = 2 = 3 = 0
D) 1 = 2 = 3
A) 1 + 2 + 3 = 0
B) 1 + 2 + 3 0
C) 1 = 2 = 3 = 0
D) 1 = 2 = 3

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
44
The distribution of the test statistic for analysis of variance is the:
A) normal distribution.
B) Student t-distribution.
C) F-distribution.
D) None of these choices.
A) normal distribution.
B) Student t-distribution.
C) F-distribution.
D) None of these choices.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
45
Consider the following ANOVA table:  The number of treatments is
The number of treatments is
A) 13
B) 5
C) 3
D) 12
 The number of treatments is
The number of treatments isA) 13
B) 5
C) 3
D) 12

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
46
In one-way analysis of variance, within-treatments variation is measured by:
A) sum of squares for error.
B) sum of squares for treatments.
C) total sum of squares.
D) standard deviation.
A) sum of squares for error.
B) sum of squares for treatments.
C) total sum of squares.
D) standard deviation.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
47
How does conducting multiple t-tests compare to conducting a single F-test?
A) Multiple t-tests increases the chance of a Type I error.
B) Multiple t-tests decreases the chance of a Type I error.
C) Multiple t-tests does not affect the chance of a Type I error.
D) This comparison cannot be made without knowing the number of populations.
A) Multiple t-tests increases the chance of a Type I error.
B) Multiple t-tests decreases the chance of a Type I error.
C) Multiple t-tests does not affect the chance of a Type I error.
D) This comparison cannot be made without knowing the number of populations.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
48
For which of the following is not a required condition for ANOVA?
A) The populations are normally distributed.
B) The population variances are equal.
C) The samples are independent.
D) All of these choices are required conditions for ANOVA.
A) The populations are normally distributed.
B) The population variances are equal.
C) The samples are independent.
D) All of these choices are required conditions for ANOVA.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
49
In a completely randomized design for ANOVA, the numerator and denominator degrees of freedom are 4 and 25, respectively. The total number of observations must equal:
A) 24
B) 25
C) 29
D) 30
A) 24
B) 25
C) 29
D) 30

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
50
The value of the test statistic in a completely randomized design for ANOVA is F = 6.29. The degrees of freedom for the numerator and denominator are 5 and 10, respectively. Using an F table, the most accurate statements to be made about the p-value is that it is:
A) greater than 0.05
B) between 0.001 and 0.010.
C) between 0.010 and 0.025.
D) between 0.025 and 0.050.
A) greater than 0.05
B) between 0.001 and 0.010.
C) between 0.010 and 0.025.
D) between 0.025 and 0.050.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
51
The analysis of variance is a procedure that allows statisticians to compare two or more population:
A) proportions.
B) means.
C) variances.
D) standard deviations.
A) proportions.
B) means.
C) variances.
D) standard deviations.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
52
Consider the following ANOVA table:  The total number of observations is:
The total number of observations is:
A) 25
B) 29
C) 30
D) 32
 The total number of observations is:
The total number of observations is:A) 25
B) 29
C) 30
D) 32

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
53
One-way ANOVA is applied to independent samples taken from four normally distributed populations with equal variances. If the null hypothesis is rejected, then we can infer that
A) all population means are equal.
B) all population means differ.
C) at least two population means are equal.
D) at least two population means differ.
A) all population means are equal.
B) all population means differ.
C) at least two population means are equal.
D) at least two population means differ.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
54
In one-way ANOVA, the term 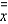 refers to the:
refers to the:
A) weighted average of the sample means.
B) sum of the sample means divided by the total number of observations.
C) sum of the population means.
D) sum of the sample means.
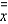 refers to the:
refers to the:A) weighted average of the sample means.
B) sum of the sample means divided by the total number of observations.
C) sum of the population means.
D) sum of the sample means.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
55
Consider the following partial ANOVA table:  The numerator and denominator degrees of freedom for the F-test (identified by asterisks) are
The numerator and denominator degrees of freedom for the F-test (identified by asterisks) are
A) 4 and 15
B) 3 and 16
C) 15 and 4
D) 16 and 3
 The numerator and denominator degrees of freedom for the F-test (identified by asterisks) are
The numerator and denominator degrees of freedom for the F-test (identified by asterisks) areA) 4 and 15
B) 3 and 16
C) 15 and 4
D) 16 and 3

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
56
In one-way analysis of variance, between-treatments variation is measured by the:
A) SSE
B) SS(Total)
C) SST
D) standard deviation
A) SSE
B) SS(Total)
C) SST
D) standard deviation

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
57
In the one-way ANOVA where k is the number of treatments and n is the number of observations in all samples, the number of degrees of freedom for error is:
A) k - 1
B) n -1
C) n - k
D) n -k + 1
A) k - 1
B) n -1
C) n - k
D) n -k + 1

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
58
In the one-way ANOVA where k is the number of treatments and n is the number of observations in all samples, the degrees of freedom for treatments is given by:
A) n- k
B) k - 1
C) n -1
D) n - k + 1
A) n- k
B) k - 1
C) n -1
D) n - k + 1

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
59
In one-way analysis of variance, if all the sample means are equal, then the:
A) total sum of squares is zero.
B) sum of squares for treatments is zero.
C) sum of squares for error is zero.
D) sum of squares for error equals sum of squares for treatments.
A) total sum of squares is zero.
B) sum of squares for treatments is zero.
C) sum of squares for error is zero.
D) sum of squares for error equals sum of squares for treatments.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
60
The number of degrees of freedom for the denominator in one-way ANOVA test involving 4 population means with 15 observations sampled from each population is:
A) 60
B) 19
C) 56
D) 45
A) 60
B) 19
C) 56
D) 45

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
61
Which of the following is false regarding SSB?
A) SSB stands for sum of squares for blocks.
B) SSB can help to reduce SSE.
C) SSB can help make it easier to determine whether differences exist between the treatment means.
D) All of these choices are true.
A) SSB stands for sum of squares for blocks.
B) SSB can help to reduce SSE.
C) SSB can help make it easier to determine whether differences exist between the treatment means.
D) All of these choices are true.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
62
The randomized block design with exactly two treatments is equivalent to a two-tail:
A) independent samples z-test.
B) independent samples equal-variances t-test.
C) independent samples unequal-variances t-test.
D) matched pairs t-test.
A) independent samples z-test.
B) independent samples equal-variances t-test.
C) independent samples unequal-variances t-test.
D) matched pairs t-test.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
63
Which of the following components in an ANOVA table is not additive?
A) Sum of squares
B) Degrees of freedom
C) Mean squares
D) All of these choices are additive.
A) Sum of squares
B) Degrees of freedom
C) Mean squares
D) All of these choices are additive.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
64
Which of the following statements about multiple comparison methods is false?
A) They are to be use once the F-test in ANOVA has been rejected.
B) They are used to determine which particular population means differ.
C) There are many different multiple comparison methods but all yield the same conclusions.
D) All of these choices are true.
A) They are to be use once the F-test in ANOVA has been rejected.
B) They are used to determine which particular population means differ.
C) There are many different multiple comparison methods but all yield the same conclusions.
D) All of these choices are true.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
65
Fisher's least significant difference (LSD) multiple comparison method is flawed because
A) it will increase ; the probability of committing a Type II error
B) it will increase ; the probability of committing a Type I error
C) it will increase both and , the probabilities of committing Type I and Type II errors, respectively.
D) None of these choices.
A) it will increase ; the probability of committing a Type II error
B) it will increase ; the probability of committing a Type I error
C) it will increase both and , the probabilities of committing Type I and Type II errors, respectively.
D) None of these choices.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
66
In the randomized block design for ANOVA, where k is the number of treatments and b is the number of blocks, the number of degrees of freedom for error is:
A) k - b
B) kb- 1
C) n - k - b + 1
D) None of these choices.
A) k - b
B) kb- 1
C) n - k - b + 1
D) None of these choices.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
67
In which case can an F-test be used to compare two population means?
A) For one tail tests only.
B) For two tail tests only.
C) For either one or two tail tests.
D) None of these choices.
A) For one tail tests only.
B) For two tail tests only.
C) For either one or two tail tests.
D) None of these choices.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
68
The primary interest of designing a randomized block experiment is to:
A) reduce the within-treatments variation to more easily detect differences among the treatment means.
B) increase the between-treatments variation to more easily detect differences among the treatment means.
C) reduce the variation among blocks.
D) None of these choices.
A) reduce the within-treatments variation to more easily detect differences among the treatment means.
B) increase the between-treatments variation to more easily detect differences among the treatment means.
C) reduce the variation among blocks.
D) None of these choices.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
69
The F-test statistic in a one-way ANOVA is equal to:
A) MST/MSE
B) SST/SSE
C) MSE/MST
D) SSE/SST
A) MST/MSE
B) SST/SSE
C) MSE/MST
D) SSE/SST

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
70
Which of the following statements is true?
A) A fixed-effects ANOVA refers to the analysis which includes all possible levels of a factor.
B) A random-effects ANOVA refers to the analysis where the levels included in the study represent a random sample of all levels that exist.
C) A multifactor experiment is one where there are two or more factors that define the treatments.
D) All of these choices are true.
A) A fixed-effects ANOVA refers to the analysis which includes all possible levels of a factor.
B) A random-effects ANOVA refers to the analysis where the levels included in the study represent a random sample of all levels that exist.
C) A multifactor experiment is one where there are two or more factors that define the treatments.
D) All of these choices are true.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
71
When is the Tukey multiple comparison method used?
A) To test for normality.
B) To test for differences in pairwise means.
C) To test for equality of a group of population means.
D) To test equal variances.
A) To test for normality.
B) To test for differences in pairwise means.
C) To test for equality of a group of population means.
D) To test equal variances.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
72
A randomized block design with 4 treatments and 5 blocks produced the following sum of squares values: SS(Total) = 1,951, SST = 349, SSE = 188 . The value of SSB must be:
A) 537
B) 1,763
C) 1,414
D) 1,602
A) 537
B) 1,763
C) 1,414
D) 1,602

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
73
Which of the following statements is false?
A) F = t2
B) The F-test can be used instead of a two tail t-test when you compare two population means.
C) Doing three t-tests is statistically equivalent to doing one F-test when you compare three population means.
D) All of these choices are true.
A) F = t2
B) The F-test can be used instead of a two tail t-test when you compare two population means.
C) Doing three t-tests is statistically equivalent to doing one F-test when you compare three population means.
D) All of these choices are true.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
74
Which of the following is not true of Tukey's Multiple Comparison Method?
A) It is based on the studentized range statistic to obtain the critical value needed to construct individual confidence intervals.
B) It theoretically requires that all sample sizes be equal, or at least similar.
C) It is more powerful than the LSD method.
D) All of these choices are true.
A) It is based on the studentized range statistic to obtain the critical value needed to construct individual confidence intervals.
B) It theoretically requires that all sample sizes be equal, or at least similar.
C) It is more powerful than the LSD method.
D) All of these choices are true.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
75
In Fisher's least significant difference (LSD) multiple comparison method, the LSD value will be the same for all pairs of means if:
A) all sample sizes are the same.
B) all sample means are the same.
C) all population means are the same.
D) None of these choices.
A) all sample sizes are the same.
B) all sample means are the same.
C) all population means are the same.
D) None of these choices.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
76
The numerator and denominator degrees of freedom for the F-test in a one-way ANOVA are, respectively,
A) (n - k) and (k -1)
B) (k -1) and (n -k)
C) (k - n) and (n - 1)
D) (n - 1) and (k - n)
A) (n - k) and (k -1)
B) (k -1) and (n -k)
C) (k - n) and (n - 1)
D) (n - 1) and (k - n)

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
77
The ANOVA procedure tests to determine whether differences exist between two or more population ____________________.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
78
In the randomized block design ANOVA, the sum of squares for error equals:
A) SS(Total) - SST
B) SS(Total) - SSB
C) SS(Total) -SST - SSB
D) None of these choices.
A) SS(Total) - SST
B) SS(Total) - SSB
C) SS(Total) -SST - SSB
D) None of these choices.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
79
When the objective is to compare more than two populations, the experimental design that is the counterpart of the matched pairs experiment is called a:
A) completely randomized design.
B) one-way ANOVA design.
C) randomized block design.
D) None of these choices.
A) completely randomized design.
B) one-way ANOVA design.
C) randomized block design.
D) None of these choices.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
80
The null hypothesis of ANOVA is that all the population means are ____________________.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck


