Deck 13: Multiple Regression and Correlation Analysis

Question 1

i. Violating the need for successive observations of the dependent variable to be uncorrelated is called autocorrelation. ii. If an inverse relationship exists between the dependent variable and independent variables, the regression coefficients for the independent variables are negative.
iii. Given a multiple linear equation Y' = 5.1 + 2.2X₁ - 3.5X₂, assuming other things are held constant, an increase in one unit of the second independent variable will cause a -3.5 unit change in Y.

A) (i), (ii), and (iii) are all correct statements.
B) (i) and (ii) are correct statements but not (iii).
C) (i) and (iii) are correct statements but not (ii).
D) (ii) and (iii) are correct statements but not (i).
E) (i), (ii), and (iii) are all false statements.

Answer 1

(i), (ii), and (iii) are all correct statements.

Question 2

Angela Chou has been asked to investigate the determinants of poverty in Ontario communities. She collected data on 60 communities from Statistics Canada. She selected the percentage of poor persons living under the poverty line [Poor (%)], measured by Low Income Cut-Off, designed by Statistics Canada as a measure of poverty for a community, as the dependent variable. The independent variables selected are percent of single families in each community, the unemployment rate in each community, and percent of population in the community holding a bachelor's degree as their highest level of education attained. Determine the regression equation.

A) Poor (%) = -3.81 + 0.798 Single-Families (%) + 0.624 Unemployment Rate (%) - 0.170 Bachelor's Degree (%)
B) Poor (%) = -3.88 + 0.798 Single-Families (%) + 0.625 Unemployment Rate (%) - 0.170 Bachelor's Degree (%)
C) Poor (%) = 3.88 + 0.798 Single-Families (%) + 0.625 Unemployment Rate (%) - 0.170 Bachelor's Degree (%)
D) Poor (%) = -3.88 - 0.798 Single-Families (%) - 0.625 Unemployment Rate (%) - 0.170 Bachelor's Degree (%)
E) Poor (%) = 3.88 + 0.798 Single-Families (%) + 0.625 Unemployment Rate (%) + 0.170 Bachelor's Degree (%)

Answer 2

Poor (%) = -3.88 + 0.798 Single-Families (%) + 0.625 Unemployment Rate (%) - 0.170 Bachelor's Degree (%)

Question 3

i. Multiple regression is used when two or more independent variables are used to predict a value of a single dependent variable. ii. The values ofb₁, b₂andb₃in a multiple regression equation are called the net regression coefficients. They indicate the change in the predicted value for a unit change in one X when the other X variables are held constant.
iii. Autocorrelation often happens when data has been collected over periods of time.

A) (i), (ii), and (iii) are all correct statements.
B) (i) and (ii) are correct statements but not (iii).
C) (i) and (iii) are correct statements but not (ii).
D) (ii) and (iii) are correct statements but not (i).
E) (i), (ii), and (iii) are all false statements.

Answer 3

(i), (ii), and (iii) are all correct statements.

Question 4

Angela Chou has been asked to investigate the determinants of poverty in Ontario communities. She collected data on 60 communities from Statistics Canada. She selected the percentage of poor persons living under the poverty line [Poor (%)], measured by Low Income Cut-Off, designed by Statistics Canada as a measure of poverty for a community, as the dependent variable. The independent variables selected are percent of single families in each community, the unemployment rate in each community, percent of population in the community holding a bachelor's degree as their highest level of education attained, and percent of population holding a High School Diploma as their highest level of education attained. Given the regression equation Poor (%) = -3.81 + 0.798 Single-Families (%) + 0.624 Unemployment Rate (%) - 0.170 Bachelor's Degree (%) - 0.003 High School (%)
Interpret the numbers 3.81 and 0.798.

A) As the % of Single Families in an Ontario community increases, the % of poor families increase as well, with a maximum of 3.81% of the population being poor.
B) As the % of Single Families in an Ontario community increases, the % of poor families decrease.
C) There are 3.81% poor families and 0.798 Single-Families in Ontario communities.
D) 3.81 is the y-intercept. When all of the dependent variables have a value of zero, we can expect that 3.81% of the community to be poor. 0.789 indicates that for an extra 0.789% of poor families in a community, we can expect that the % of single families will increase by 1%.
E) When all of the independent variables have a value of zero, we can expect that -3.81% of the community to be poor, i.e. 0%. The 0.798 indicates that for each extra % of single families in a community, we can expect that the % poor will increase by almost 0.8%.

Question 5

Angela Chou has been asked to investigate the determinants of poverty in Ontario communities. She collected data on 60 communities from Statistics Canada. She selected the percentage of poor persons living under the poverty line [Poor (%)], measured by Low Income Cut-Off, designed by Statistics Canada as a measure of poverty for a community, as the dependent variable. The independent variables selected are percent of single families in each community, the unemployment rate in each community, percent of population in the community holding a bachelor's degree as their highest level of education attained, and percent of population holding a High School Diploma as their highest level of education attained. Given the regression equation Poor (%) = -3.81 + 0.798 Single-Families (%) + 0.624 Unemployment Rate (%) - 0.170 Bachelor's Degree (%) - 0.003 High School (%).
How many dependent variables are there in this regression?

A) 1
B) 2
C) 3
D) 4
E) 5

Question 6

The information below is from the multiple regression analysis computer output for 28 teams in Major League Baseball. The model is designed to predict wins using attendance, payroll, batting average, home runs, stolen bases, errors, and team ERA. 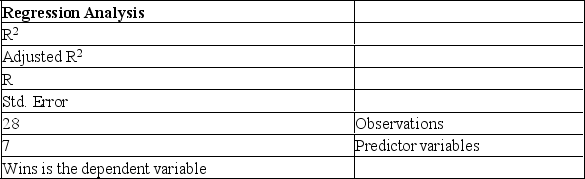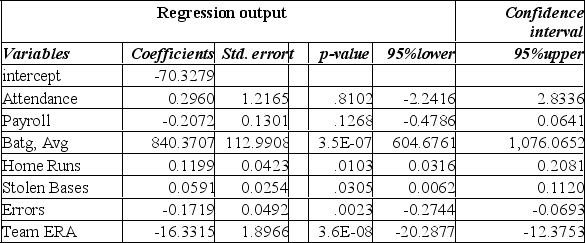Predict the number of wins for a team with:
BATAVG = 0.260 HOMERUNS = 150 ERA = 3
STOLENBASE = 100 ERROR = 100
PAYROLL = 25(million)
ATTENDANCE = 3(million)

A) 77
B) 102
C) 187
D) 210
E) 186

Question 7

How is the Y intercept in the multiple regression equation represented?

A) b₁
B) x₁
C) b₂
D) x₂
E) a

Question 8

A manager at a local bank analyzed the relationship between monthly salary and three independent variables: length of service (measured in months), gender (0 = female, 1 = male) and job type (0 = clerical, 1 = technical). The following ANOVA summarizes the regression results: 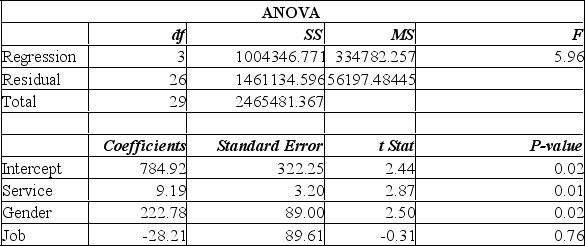In the regression model, which of the following are dummy variables?

A) Intercept
B) Service
C) Service and gender
D) Gender and job
E) Service, gender, and job

Question 9

i. Multiple regression analysis examines the relationship of several dependent variables on the independent variable. ii. A multiple regression equation defines the relationship between the dependent variable and the independent variables in the form of an equation.
iii. Autocorrelation often happens when data has been collected over periods of time.

A) (i), (ii), and (iii) are all correct statements.
B) (i) and (ii) are correct statements but not (iii).
C) (i) and (iii) are correct statements but not (ii).
D) (ii) and (iii) are correct statements but not (i).
E) (i), (ii), and (iii) are all false statements.

Question 10

i. The values ofb₁, b₂ and b₃in a multiple regression equation are called the net regression coefficients. They indicate the change in the predicted value for a unit change in one X when the other X variables are held constant. ii. Multiple regression analysis examines the relationship of several dependent variables on the independent variable.
iii. A multiple regression equation defines the relationship between the dependent variable and the independent variables in the form of an equation.

A) (i), (ii), and (iii) are all correct statements.
B) (i) and (ii) are correct statements but not (iii).
C) (i) and (iii) are correct statements but not (ii).
D) (ii) and (iii) are correct statements but not (i).
E) (i), (ii), and (iii) are all false statements.

Question 11

i. A multiple regression equation defines the relationship between the dependent variable and the independent variables in the form of an equation. ii. Autocorrelation often happens when data has been collected over periods of time.
iii. Homoscedasticity occurs when the variance of the residuals (Y - Y') is different for different values of Y'.

A) (i), (ii), and (iii) are all correct statements.
B) (i) and (ii) are correct statements but not (iii).
C) (i) and (iii) are correct statements but not (ii).
D) (ii) and (iii) are correct statements but not (i).
E) (i), (ii), and (iii) are all false statements.

Question 12

Multiple regression analysis is applied when analyzing the relationship between

A) an independent variable and several dependent variables.
B) a dependent variable and several independent variables.
C) several dependent variables and several independent variables.
D) several regression equations and a single sample.

Question 13

i. The values of b₁, b₂ and b₃in a multiple regression equation are called the net regression coefficients. They indicate the change in the predicted value for a unit change in one X when the other X variables are held constant. ii. A multiple regression equation defines the relationship between the dependent variable and the independent variables in the form of an equation.
iii. If an inverse relationship exists between the dependent variable and independent variables, the regression coefficients for the independent variables are positive.

A) (i), (ii), and (iii) are all correct statements.
B) (i) and (ii) are correct statements but not (iii).
C) (i) and (iii) are correct statements but not (ii).
D) (ii) and (iii) are correct statements but not (i).
E) (i), (ii), and (iii) are all false statements.

Question 14

i. Autocorrelation often happens when data has been collected over periods of time. ii. Homoscedasticity occurs when the variance of the residuals (Y - Y') is different for different values of Y'.
iii. Violating the need for successive observations of the dependent variable to be uncorrelated is called autocorrelation.

A) (i), (ii), and (iii) are all correct statements.
B) (i) and (ii) are correct statements but not (iii).
C) (i) and (iii) are correct statements but not (ii).
D) (ii) and (iii) are correct statements but not (i).
E) (i), (ii), and (iii) are all false statements.

Question 15

i. If an inverse relationship exists between the dependent variable and independent variables, the regression coefficients for the independent variables are positive. ii. Given a multiple linear equation Y' = 5.1 + 2.2X₁ - 3.5X₂, assuming other things are held constant, an increase of one unit in the second independent variable will cause a -3.5 unit change in Y.
iii. When the variance of the differences between the actual and the predicted values of the dependent variable are approximately the same, the variables are said to exhibit homoscedasticity.

A) (i), (ii), and (iii) are all correct statements.
B) (i) and (ii) are correct statements but not (iii).
C) (i) and (iii) are correct statements but not (ii).
D) (ii) and (iii) are correct statements but not (i).
E) (i), (ii), and (iii) are all false statements.

Question 16

Angela Chou has been asked to investigate the determinants of poverty in Ontario communities. She collected data on 60 communities from Statistics Canada. She selected the percentage of poor persons living under the poverty line [Poor (%)], measured by Low Income Cut-Off, designed by Statistics Canada as a measure of poverty for a community, as the dependent variable. The independent variables selected are percent of single families in each community, the unemployment rate in each community, percent of population in the community holding a bachelor's degree as their highest level of education attained, and percent of population holding a High School Diploma as their highest level of education attained. Given the regression equation Poor (%) = -3.81 + 0.798 Single-Families (%) + 0.624 Unemployment Rate (%) - 0.170 Bachelor's Degree (%) - 0.003 High School (%).
What is the estimated percentage of poor persons living below the poverty line in a community with 5% of the community as single-families, a 5% unemployment rate, only 5% holding a Bachelor's Degree and 25% having High School as their highest attained educational level?

A) 2.375
B) -2.375
C) 11.845
D) -11.845

Question 17

i. Multiple regression is used when two or more independent variables are used to predict a value of a single dependent variable. ii. The values of b₁, b_2, and b₃ in a multiple regression equation are called the net regression coefficients. They indicate the change in the predicted value for a unit change in one X when the other X variables are held constant.
iii. Multiple regression analysis examines the relationship of several dependent variables on the independent variable.

A) (i), (ii), and (iii) are all correct statements.
B) (i) and (ii) are correct statements but not (iii).
C) (i) and (iii) are correct statements but not (ii).
D) (ii) and (iii) are correct statements but not (i).
E) (i), (ii), and (iii) are all false statements.

Question 18

Angela Chou has been asked to investigate the determinants of poverty in Ontario communities. She collected data on 60 communities from Statistics Canada. She selected the percentage of poor persons living under the poverty line [Poor (%)], measured by Low Income Cut-Off, designed by Statistics Canada as a measure of poverty for a community, as the dependent variable. The independent variables selected are percent of single families in each community, the unemployment rate in each community, percent of population in the community holding a bachelor's degree as their highest level of education attained, and percent of population holding a High School Diploma as their highest level of education attained. Given the regression equation Poor (%) = -3.81 + 0.798 Single-Families (%) + 0.624 Unemployment Rate (%) - 0.170 Bachelor's Degree (%) - 0.003 High School (%)
Which single event would have the strongest effect in reducing the % poor in Ontario?

A) Decreasing the % of single families by 5%.
B) Decreasing the Unemployment rate by 5%.
C) Increasing the % of persons with a Bachelor's Degree by 10%.
D) Decreasing the % of persons with a High School Diploma by 40%.
E) Increasing the % of persons with a Bachelor's Degree by 15%.

Question 19

The following correlations were computed as part of a multiple regression analysis that used education, job, and age to predict income. Which is the dependent variable?

A) Income
B) Age
C) Education
D) Job

Question 20

Angela Chou has been asked to investigate the determinants of poverty in Ontario communities. She collected data on 60 communities from Statistics Canada. She selected the percentage of poor persons living under the poverty line [Poor (%)], measured by Low Income Cut-Off, designed by Statistics Canada as a measure of poverty for a community, as the dependent variable. The independent variables selected are percent of single families in each community, the unemployment rate in each community, percent of population in the community holding a bachelor's degree as their highest level of education attained, and percent of population holding a High School Diploma as their highest level of education attained. Determine the regression equation.

A) Poor (%) = -3.81 - 0.798 Single-Families (%) + 0.624 Unemployment Rate (%) - 0.170 Bachelor's Degree (%) - 0.003 High School (%)
B) Poor (%) = -3.81 + 0.798 Single-Families (%) + 0.624 Unemployment Rate (%) + 0.170 Bachelor's Degree (%) + 0.003 High School (%)
C) Poor (%) = 3.81 + 0.798 Single-Families (%) + 0.624 Unemployment Rate (%) - 0.170 Bachelor's Degree (%) - 0.003 High School (%)
D) Poor (%) = -3.81 + 0.798 Single-Families (%) + 0.624 Unemployment Rate (%) - 0.170 Bachelor's Degree (%) - 0.003 High School (%)
E) Poor (%) = 3.81 + 0.798 Single-Families (%) - 0.624 Unemployment Rate (%) + 0.170 Bachelor's Degree (%) - 0.003 High School (%)

Question 21

A sample of General Mills employees was studied to determine their degree of satisfaction with their present life. A special index, called the index of satisfaction, was used to measure satisfaction. Six factors were studied: age at the time of first marriage (X₁), annual income (X₂), number of children living (X₃), value of all assets (X₄), status of health in the form of an index (X₅), and the average number of social activities per week (X₆). Suppose the multiple regression equation is: Y' = 16.24 + 0.017X₁ + 0.00028X₂ + 42X₃ + 0.0012X₄ + 0.09X₅ + 26.8X₆.
Explain the meaning of b₂.

A) For each additional$1,000 of annual income, their satisfaction index is expected to increase by 0.28 points.
B) For each additional$1,000 of annual income, their satisfaction index is expected to increase by 2.8 points.
C) For each additional$1,000 of annual income, their satisfaction index is expected to increase by 28 points.
D) For each additional living child, their satisfaction index is expected to increase by 42 points.
E) For each additional living child, their satisfaction index is expected to increase by 4.2 points.

Question 22

In regression analysis, the df_err = ________.

A) the sample size -1
B) the sample size -k-1
C) the number of dependent variables
D) the number of independent variables
E) the sample size-k

Question 23

The information below is from the multiple regression analysis computer output for 28 teams in Major League Baseball. The model is designed to predict wins using attendance, payroll, batting average, home runs, stolen bases, errors, and team ERA. 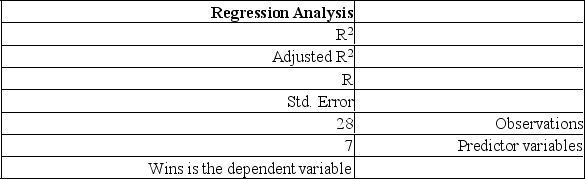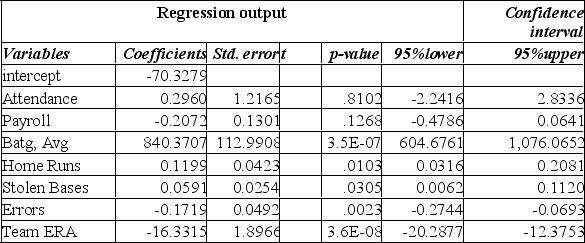The multiple correlation coefficient is:

A) 0.900
B) 0.930
C) 0.656
D) 0.867
E) 0.949

Question 24

What are the degrees of freedom associated with the regression sum of squares?

A) Number of independent variables
B) 1
C) F-ratio
D) (n - 2)

Question 25

A sample of General Mills employees was studied to determine their degree of satisfaction with their present life. A special index, called the index of satisfaction, was used to measure satisfaction. Six factors were studied: age at the time of first marriage (X₁), annual income (X₂), number of children living (X₃), value of all assets (X₄), status of health in the form of an index (X₅), and the average number of social activities per week (X₆). Suppose the multiple regression equation is: Y' = 16.24 + 0.017X₁ + 0.00028X₂ +42X₃ + 0.0012X₄ + 0.19X₅ + 26.8X₆.
What is the estimated index of satisfaction for a person who first married at 25, has an annual income of $60,000, has two children, has assets of $350,000, has in index of health status of 141, and has 2 social activities per week?

A) 777.7
B) 796.6
C) 617.9
D) 601.6
E) 769.8

Question 26

A sample of General Mills employees was studied to determine their degree of satisfaction with their present life. A special index, called the index of satisfaction, was used to measure satisfaction. Six factors were studied: age at the time of first marriage (X₁), annual income (X₂), number of children living (X₃), value of all assets (X₄), status of health in the form of an index (X₅), and the average number of social activities per week (X₆). Suppose the multiple regression equation is: Y' = 16.24 + 0.017X₁ + 0.00028X₂ +42X₃ + 0.0012X₄ + 0.19X₅ + 26.8X₆.
What is the estimated index of satisfaction for a person who first married at 25, has an annual income of $26,500, has two children, has assets of $156,000, has in index of health status of 141, and has 2.5 social activities per week?

A) 389.1
B) 421.6
C) 366.0
D) 601.6
E) 769.8

Question 27

A sample of General Mills employees was studied to determine their degree of satisfaction with their present life. A special index, called the index of satisfaction, was used to measure satisfaction. Six factors were studied: age at the time of first marriage (X₁), annual income (X₂), number of children living (X₃), value of all assets (X₄), status of health in the form of an index (X₅), and the average number of social activities per week (X₆). Suppose the multiple regression equation is: Y' = 16.24 + 0.017X₁ + 0.00028X₂ +42X₃ + 0.0012X₄ + 0.09X₅ + 26.8X₆.
Explain the meaning of b₄.

A) For each additional living child, their satisfaction index is expected to increase by 42 points.
B) For each additional$1,000 of annual income, their satisfaction index is expected to increase by 0.028 points.
C) For each additional$10,000 in assets, their satisfaction index is expected to increase by 0.12 points.
D) For each additional$10,000 in assets, their satisfaction index is expected to increase by 1.2 points.
E) For each additional$10,000 in assets, their satisfaction index is expected to increase by 12 points.

Question 28

A sample of General Mills employees was studied to determine their degree of satisfaction with their present life. A special index, called the index of satisfaction, was used to measure satisfaction. Six factors were studied: age at the time of first marriage (X₁), annual income (X₂), number of children living (X₃), value of all assets (X₄), status of health in the form of an index (X₅), and the average number of social activities per week (X₆). Suppose the multiple regression equation is: Y' = 16.24 + 0.017X₁ + 0.00028X₂ +42X₃ + 0.0012X₄ + 0.09X₅ + 26.8X₆.
Explain the meaning of b₃.

A) For each additional living child, their satisfaction index is expected to increase by 4.2 points.
B) For each additional living child, their satisfaction index is expected to increase by 42 points.
C) For each additional living child, their satisfaction index is expected to increase by 0.42 points.
D) For each additional$1,000 of annual income, their satisfaction index is expected to increase by 0.028 points.
E) For each additional$1,000 of annual income, their satisfaction index is expected to increase by 2.8 points.

Question 29

A sample of General Mills employees was studied to determine their degree of satisfaction with their present life. A special index, called the index of satisfaction, was used to measure satisfaction. Six factors were studied: age at the time of first marriage (X₁), annual income (X₂), number of children living (X₃), value of all assets (X₄), status of health in the form of an index (X₅), and the average number of social activities per week (X₆). Suppose the multiple regression equation is: Y' = 16.24 + 0.017X₁ + 0.00028X₂ + 42X₃ + 0.0012X₄ + 0.19X₅ + 26.8X₆.
What is the estimated index of satisfaction for a person who first married at 25, has an annual income of $100,000, has two children, has assets of $500,000, has in index of health status of 141, and has 2 social activities per week?

A) 777.7
B) 796.6
C) 588.6
D) 601.6
E) 809.1

Question 30

If the correlation between two variables X and Y, is +0.67, what is the regression coefficient for these two variables?

A) +0.67
B) > 0
C) < 0
D) = 0

Question 31

In a regression analysis, three independent variables are used in the equation based on a sample of forty observations. What are the degrees of freedom associated with the F-statistic?

A) 3 and 39
B) 4 and 40
C) 3 and 36
D) 2 and 39

Question 32

In regression analysis, the df_reg = ________.

A) the sample size - 1
B) the sample size -k-1
C) the number of dependent variables
D) the number of independent variables
E) the sample size-k

Question 33

A sample of General Mills employees was studied to determine their degree of satisfaction with their present life. A special index, called the index of satisfaction, was used to measure satisfaction. Six factors were studied: age at the time of first marriage (X₁), annual income (X₂), number of children living (X₃), value of all assets (X₄), status of health in the form of an index (X₅), and the average number of social activities per week (X₆). Suppose the multiple regression equation is: Y' = 16.24 + 0.017X₁ + 0.00028X₂ +42X₃ + 0.0012X₄ + 0.19X₅ + 26.8X₆.
What is the estimated index of satisfaction for a person who first married at 25, has an annual income of $100,000, has two children, has assets of $500,000, has in index of health status of 141, and has 3 social activities per week?

A) 777.7
B) 835.9
C) 588.6
D) 601.6
E) 769.8

Question 34

A sample of General Mills employees was studied to determine their degree of satisfaction with their present life. A special index, called the index of satisfaction, was used to measure satisfaction. Six factors were studied: age at the time of first marriage (X₁), annual income (X₂), number of children living (X₃), value of all assets (X₄), status of health in the form of an index (X₅), and the average number of social activities per week (X₆). Suppose the multiple regression equation is: Y' = 16.24 + 0.017X₁ + 0.00028X₂ +42X₃ + 0.0012X₄ + 0.09X₅ + 26.8X₆.
Explain the meaning of b₅.

A) For each additional10 points on the health status index, their satisfaction index is expected to increase by 9 points.
B) For each additional10 points on the health status index, their satisfaction index is expected to increase by 0.09 points.
C) For each additional10 points on the health status index, their satisfaction index is expected to increase by 0.9 points.
D) For each additional10 points on the health status index, their satisfaction index is expected to drop by 0.09 points.
E) For each additional10 points on the health status index, their satisfaction index is expected to decrease by 9 points.

Question 35

A sample of General Mills employees was studied to determine their degree of satisfaction with their present life. A special index, called the index of satisfaction, was used to measure satisfaction. Six factors were studied: age at the time of first marriage (X₁), annual income (X₂), number of children living (X₃), value of all assets (X₄), status of health in the form of an index (X₅), and the average number of social activities per week (X₆). Suppose the multiple regression equation is: Y' = 16.24 + 0.017X₁ + 0.00028X₂ + 42X₃+ 0.0012X₄ + 0.19X₅ + 26.8X₆.
What is the estimated index of satisfaction for a person who first married at 25, has an annual income of $100,000, has two children, has assets of $500,000, has in index of health status of 141, and has 3.5 social activities per week?

A) 777.7
B) 796.6
C) 849.3
D) 601.6
E) 769.8

Question 36

A sample of General Mills employees was studied to determine their degree of satisfaction with their present life. A special index, called the index of satisfaction, was used to measure satisfaction. Six factors were studied: age at the time of first marriage (X₁), annual income (X₂), number of children living (X₃), value of all assets (X₄), status of health in the form of an index (X₅), and the average number of social activities per week (X₆). Suppose the multiple regression equation is: Y' = 16.24 + 0.017X₁ + 0.00028X₂ +42X₃ + 0.0012X₄ + 0.09X₅ + 26.8X₆.
Explain the meaning of b₆.

A) For each additional social activity per week, their satisfaction index is expected to increase by 26.8 points.
B) For each additional social activity per week, their satisfaction index is expected to increase by 2.68 points.
C) For each additional10 points on the health status index, their satisfaction index is expected to increase by 0.9 points.
D) For each additional$10,000 in assets, their satisfaction index is expected to increase by 12 points.
E) For each additional living child, their satisfaction index is expected to increase by 42 points.

Question 37

A sample of General Mills employees was studied to determine their degree of satisfaction with their present life. A special index, called the index of satisfaction, was used to measure satisfaction. Six factors were studied: age at the time of first marriage (X₁), annual income (X₂), number of children living (X₃), value of all assets (X₄), status of health in the form of an index (X₅), and the average number of social activities per week (X₆). Suppose the multiple regression equation is: Y' = 16.24 + 0.017X₁ + 0.00028X₂ +42X₃ + 0.0012X₄ + 0.19X₅ + 26.8X₆
What is the estimated index of satisfaction for a person who first married at 25, has an annual income of $46,000, has two children, has assets of $200,000, has in index of health status of 141, and has 2.5 social activities per week?

A) 368.3
B) 447.3
C) 366.0
D) 601.6
E) 769.8

Question 38

For a unit change in the first independent variable with other things being held constant, what change can be expected in the dependent variable in the multiple regression equation Y' = 5.2 + 6.3X₁- 7.1X₂?

A) -7.1
B) +6.3
C) +5.2
D) +4.4

Question 39

A sample of General Mills employees was studied to determine their degree of satisfaction with their present life. A special index, called the index of satisfaction, was used to measure satisfaction. Six factors were studied: age at the time of first marriage (X₁), annual income (X₂), number of children living (X₃), value of all assets (X₄), status of health in the form of an index (X₅), and the average number of social activities per week (X₆). Suppose the multiple regression equation is: Y' = 16.24 + 0.017X₁ + 0.00028X₂ +42X₃ + 0.0012X₄ + 0.19X₅ + 26.8X₆.
What is the estimated index of satisfaction for a person who first married at 25, has an annual income of $46,000, has two children, has assets of $350,000, has in index of health status of 141, and has 2.5 social activities per week?

A) 368.3
B) 421.6
C) 366.0
D) 627.3
E) 769.8

Question 40

If there are four independent variables in a multiple regression equation, there are also four

A) Y-intercepts.
B) regression coefficients.
C) dependent variables.
D) constant terms.

Question 41

i. The coefficient of multiple determination reports the strength of the association between the dependent variable and the set of independent variables. ii. The multiple standard error of estimate for two independent variables measures the variation about a regression plane.
iii. A multiple coefficient of determination equaling -0.76 is definitely possible.

A) (i), (ii), and (iii) are all correct statements.
B) (i) and (ii) are correct statements but not (iii).
C) (i) and (iii) are correct statements but not (ii).
D) (ii) and (iii) are correct statements but not (i).
E) (i), (ii), and (iii) are all false statements.

Question 42

If the coefficient of multiple determinations is 0.81, what percent of variation is not explained?

A) 19%
B) 90%
C) 66%
D) 81%

Question 43

i. The multiple coefficient of determination, R², reports the proportion of the variation in Y that is not explained by the variation in the set of independent variables. ii. The coefficient of multiple determination reports the strength of the association between the dependent variable and the set of independent variables.
iii. The multiple standard error of estimate for two independent variables measures the variation about a regression plane.

A) (i), (ii), and (iii) are all correct statements.
B) (i) and (ii) are correct statements but not (iii).
C) (i) and (iii) are correct statements but not (ii).
D) (ii) and (iii) are correct statements but not (i).
E) (i), (ii), and (iii) are all false statements.

Question 44

What happens as the scatter of data values about the regression plane increases?

A) Standard error of estimate increases.
B) R²decreases.
C) (1 -R²) decreases.
D) Residual sum of squares decreases.
E) (1 -R²), residual sum of squares and standard error of estimate all increase, andR²decreases.

Question 45

The coefficient of determination measures the proportion of

A) explained variation relative to total variation.
B) variation due to the relationship among variables.
C) error variation relative to total variation.
D) variation due to regression.

Question 46

i. A coefficient of multiple determination equaling -0.76 is definitely possible. ii. Multiple R² measures the proportion of explained variation relative to total variation.
iii. The number of degrees of freedom associated with the regression sum of squares in the regression equation model equals the number of independent variables.

A) (i), (ii), and (iii) are all correct statements.
B) (i) and (ii) are correct statements but not (iii).
C) (i) and (iii) are correct statements but not (ii).
D) (ii) and (iii) are correct statements but not (i).
E) (i), (ii), and (iii) are all false statements.

Question 47

What is the measurement of explained variation?

A) Coefficient of multiple determination
B) Coefficient of multiple nondetermination
C) Regression coefficient
D) Correlation matrix

Question 48

What is the range of values for multiple R?

A) -100% to - 100% inclusive
B) -100% to 0% inclusive
C) 0% to + 100% inclusive
D) Unlimited range

Question 49

If a multiple regression analysis is based on ten independent variables collected from a sample of 125 observations, what will be the value of the denominator in the calculation of the multiple standard error of estimate?

A) 125
B) 10
C) 114
D) 115

Question 50

The information below is from the multiple regression analysis computer output for 28 teams in Major League Baseball. The model is designed to predict wins using attendance, payroll, batting average, home runs, stolen bases, errors, and team ERA. 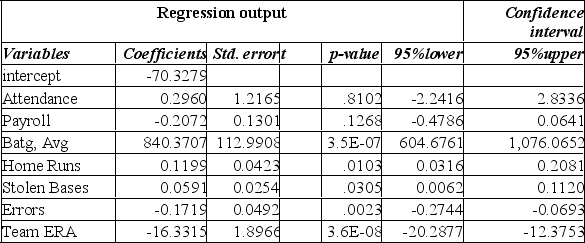The standard error of estimate is:

A) 4.467
B) 5.698
C) 5.864
D) 19.977
E) 15.917

Question 51

i. The multiple coefficient of determination, R², reports the proportion of the variation in Y that is explained by the variation in the set of independent variables. ii. The coefficient of multiple determination reports the strength of the association between the dependent variable and the set of independent variables.
iii. A coefficient of multiple determination equaling -0.76 is definitely possible.

A) (i), (ii), and (iii) are all correct statements.
B) (i) and (ii) are correct statements but not (iii).
C) (i) and (iii) are correct statements but not (ii).
D) (ii) and (iii) are correct statements but not (i).
E) (i), (ii), and (iii) are all false statements.

Question 52

i. The multiple standard error of estimate measures the variation about the regression plane when two independent variables are considered. ii. The multiple coefficient of determination, R², reports the proportion of the variation in Y that is not explained by the variation in the set of independent variables.
iii. The coefficient of multiple determination reports the strength of the association between the dependent variable and the set of independent variables.

A) (i), (ii), and (iii) are all correct statements.
B) (i) and (ii) are correct statements but not (iii).
C) (i) and (iii) are correct statements but not (ii).
D) (ii) and (iii) are correct statements but not (i).
E) (i), (ii), and (iii) are all false statements.

Question 53

i. Multiple R² measures the proportion of explained variation. ii. 90% of total variation in the dependent variable is explained by the independent variable for a multiple R² = 0.90.
iii. The multiple standard error of estimate measures the variation about the regression plane when two independent variables are considered.

A) (i), (ii), and (iii) are all correct statements.
B) (i) and (ii) are correct statements but not (iii).
C) (i) and (iii) are correct statements but not (ii).
D) (ii) and (iii) are correct statements but not (i).
E) (i), (ii), and (iii) are all false statements.

Question 54

i. 90% of total variation in the dependent variable is explained by the independent variable for a multiple R² = 0.90. ii. The multiple standard error of estimate measures the variation about the regression plane when two independent variables are considered.
iii. The multiple coefficient of determination, R², reports the proportion of the variation in Y that is not explained by the variation in the set of independent variables.

A) (i), (ii), and (iii) are all correct statements.
B) (i) and (ii) are correct statements but not (iii).
C) (i) and (iii) are correct statements but not (ii).
D) (ii) and (iii) are correct statements but not (i).
E) (i), (ii), and (iii) are all false statements.

Question 55

A manager at a local bank analyzed the relationship between monthly salary and three independent variables: length of service (measured in months), gender (0 = female, 1 = male) and job type (0 = clerical, 1 = technical). The following ANOVA summarizes the regression results: 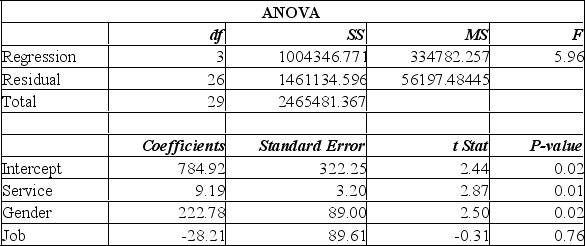Based on the ANOVA, the multiple coefficient of determination is

A) 5.957%.
B) 59.3%.
C) 40.7%.
D) cannot be computed.

Question 56

Which test statistic do we apply to test the null hypothesis that the multiple regression coefficients are all zero?

A) z
B) t
C) F
D) SPSS-X

Question 57

i. The multiple standard error of estimate for two independent variables measures the variation about a regression plane. ii. A multiple coefficient of determination equaling -0.76 is definitely possible.
iii. Multiple R² measures the proportion of explained variation relative to total variation.

A) (i), (ii), and (iii) are all correct statements.
B) (i) and (ii) are correct statements but not (iii).
C) (i) and (iii) are correct statements but not (ii).
D) (ii) and (iii) are correct statements but not (i).
E) (i), (ii), and (iii) are all false statements.

Question 58

What does the multiple standard error of estimate measure?

A) Change in Y' for a change in X₁.
B) Variation of the data points between Y and Y'.
C) Variation due to the relationship between the dependent and independent variables.
D) Amount of explained variation.

Question 59

How is the degree of association between the set of independent variables and the dependent variable is measured?

A) Confidence intervals
B) Autocorrelation
C) Coefficient of multiple determination
D) Standard error of estimate

Question 60

i. The multiple standard error of estimate measures the variation about the regression plane when two independent variables are considered. ii. A coefficient of multiple determination equaling -0.76 is definitely possible.
iii. The number of degrees of freedom associated with the regression sum of squares in the regression equation model equals the number of independent variables.

A) (i), (ii), and (iii) are all correct statements.
B) (i) and (ii) are correct statements but not (iii).
C) (i) and (iii) are correct statements but not (ii).
D) (ii) and (iii) are correct statements but not (i).
E) (i), (ii), and (iii) are all false statements.

Question 61

The information below is from the multiple regression analysis computer output for 28 teams in Major League Baseball. The model is designed to predict wins using attendance, payroll, batting average, home runs, stolen bases, errors, and team ERA. 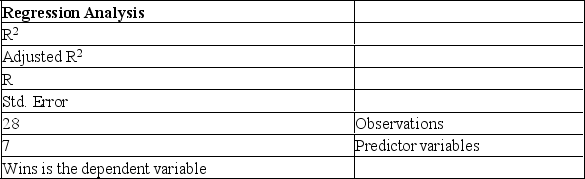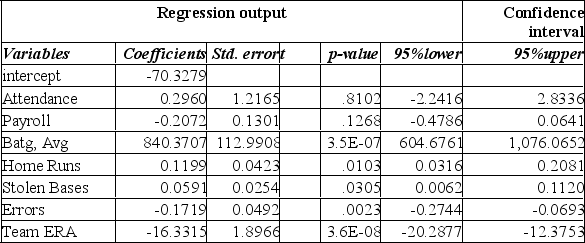The critical value of F to be used in the global test of the model is: (5% level of significance)

A) 2.51
B) 2.58
C) 3.70
D) 5.57
E) 3.39

Question 62

What test investigates whether all the independent variables have zero net regression coefficients?

A) Multicollinearity
B) Autocorrelation
C) Global
D) Pearson

Question 63

Angela Chou has been asked to investigate the determinants of poverty in Ontario communities. She collected data on 60 communities from Statistics Canada. She selected the percentage of poor persons living under the poverty line [Poor (%)], measured by Low Income Cut-Off, and designed by Statistics Canada as a measure of poverty for a community, as the dependent variable. The independent variables selected are percent of single families in each community, the unemployment rate in each community, percent of population in the community holding a bachelor's degree as their highest level of education attained, and percent of population holding a High School Diploma as their highest level of education attained. Using the output below, determine which variable Angela should consider deleting.

A) It doesn't matter which she uses, the results are virtually the same in any case.
B) Angela should delete the high school information, because the P-value is over 0.05.
C) Angela should delete the bachelor'sdegree information, because the P-value is close to 0.05.
D) Angela should delete the unemployment rate information because the P-value is 0.00.
E) Angela should exclude the single-family and unemployment information because the P-value values are 0.

Question 64

Angela Chou has been asked to investigate the determinants of poverty in Ontario communities. She collected data on 60 communities from Statistics Canada. She selected the percentage of poor persons living under the poverty line [Poor (%)], measured by Low Income Cut-Off, designed by Statistics Canada as a measure of poverty for a community, as the dependent variable. The independent variables selected are percent of single families in each community, the unemployment rate in each community, percent of population in the community holding a bachelor's degree as their highest level of education attained, and percent of population holding a High School Diploma as their highest level of education attained. Using the outputs below for this data set, determine whether Angela should use the model with the high school data included, or the data without the high school data, and why.

A) It doesn't matter which she uses, the results are virtually the same in either case.
B) Angela should use the data that includes the high school information, because more information is always better than less information.
C) Angela should use the data that includes the high school information, because the calculated F value is lower.
D) Angela should include the high school data because the P-value is 0.977, close to 1.
E) Angela should exclude the high school data because the adjusted R-squared value is a little higher than in the data that includes the high school information.

Question 65

The best example of a null hypothesis for a global test of a multiple regression model is:

A) H₀: $\beta$ ₁ = $\beta$ ₂ = $\beta$ ₃ = $\beta$ ₄.
B) H₀: $\mu$ ₁ = $\mu$ ₂ = $\mu$ ₃ = $\mu$ ₄.
C) H₀: $\beta$ ₁ = 0.
D) if F is greater than 20.00 then reject.

Question 66

The best example of an alternate hypothesis for a global test of a multiple regression model is:

A) H₁: $\beta$ ₁ = $\beta$ ₂ = $\beta$ ₃ = $\beta$ ₄.
B) H₁: $\beta$ ₁ $\neq$$\beta$ ₂ $\neq$$\beta$ ₃ $\neq$$\beta$ ₄.
C) H₁: Not all the $\beta$ 's are 0.
D) if F is less than 20.00 then fail to reject.

Question 67

The information below is from the multiple regression analysis computer output for 28 teams in Major League Baseball. The model is designed to predict wins using attendance, payroll, batting average, home runs, stolen bases, errors, and team ERA. 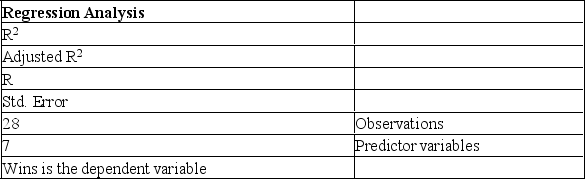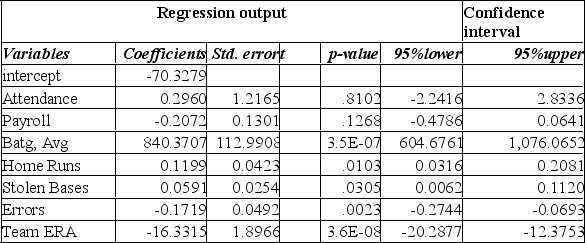The number of degrees of freedom to be used in determining the critical value of t to be used in a hypothesis test of the regression coefficients is:

A) 27
B) 26
C) 22
D) 21
E) 20

Question 68

The best example of a null hypothesis for testing an individual regression coefficient is:

A) H₀: $\beta$ ₁ = $\beta$ ₂ = $\beta$ ₃ = $\beta$ ₄.
B) H₀: $\mu$ ₁ = $\mu$ ₂ = $\mu$ ₃ = $\mu$ ₄.
C) H₀: $\beta$ ₁ = 0.
D) if F is greater than 20.00 then reject.

Question 69

A manager at a local bank analyzed the relationship between monthly salary and three independent variables: length of service (measured in months), gender (0 = female, 1 = male) and job type (0 = clerical, 1 = technical). The following ANOVA summarizes the regression results: 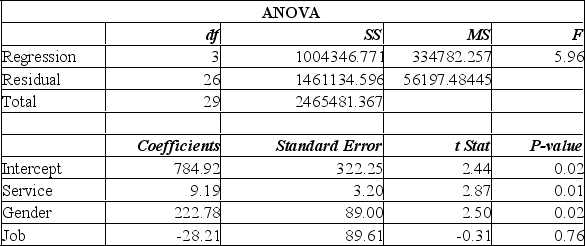Based on the ANOVA and a 0.05 significance level, the global null hypothesis test of the multiple regression model.

A) will be rejected and conclude that monthly salary is related to all of the independent variables.
B) will be rejected and conclude that monthly salary is related to at least one of the independent variables.
C) will not be rejected.
D) will show a high multiple coefficient of determination.

Question 70

The information below is from the multiple regression analysis computer output for 28 teams in Major League Baseball. The model is designed to predict wins using attendance, payroll, batting average, home runs, stolen bases, errors, and team ERA. 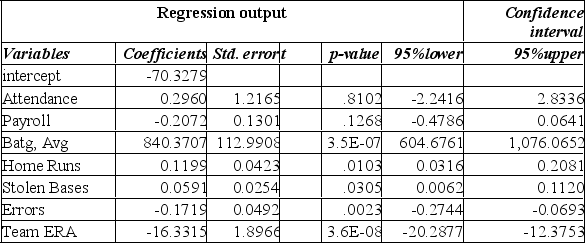The computed F for the global test is:

A) 7.802
B) 25.695
C) 15.790
D) 26.981
E) 114.779

Question 71

Hypotheses concerning individual regression coefficients are tested using which statistic?

A) t-statistic
B) z-statistic
C) $\chi$ ²(chi-square statistic)
D) H

Question 72

i. A variable whose possible outcomes are coded as a "1" or a "0" is called a dummy variable. ii. A dummy variable is added to the regression equation to control for error.
iii. If the null hypothesis $\beta$ ₄ = 0 is not rejected, then the independent variable X₄ has no effect in predicting the dependent variable.

A) (i), (ii), and (iii) are all correct statements.
B) (i) and (ii) are correct statements but not (iii).
C) (i) and (iii) are correct statements but not (ii).
D) (ii) and (iii) are correct statements but not (i).
E) (i), (ii), and (iii) are all false statements.

Question 73

i. If the null hypothesis $\beta$ ₄ = 0 is not rejected, then the independent variable X₄ has a strong effect in predicting the dependent variable. ii. A dummy variable is added to the regression equation to control for error.
iii. A variable whose possible outcomes are coded as a "1" or a "0" is called a strong independent variable.

A) (i), (ii), and (iii) are all correct statements.
B) (i) and (ii) are correct statements but not (iii).
C) (i) and (iii) are correct statements but not (ii).
D) (ii) and (iii) are correct statements but not (i).
E) (i), (ii), and (iii) are all false statements.

Question 74

A manager at a local bank analyzed the relationship between monthly salary and three independent variables: length of service (measured in months), gender (0 = female, 1 = male) and job type (0 = clerical, 1 = technical). The following ANOVA summarizes the regression results: 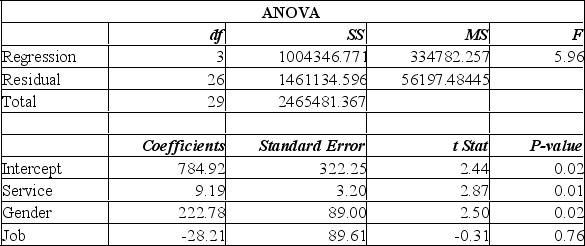Based on the hypothesis tests for the individual regression coefficients,

A) all the regression coefficients are not equal to zero.
B) "job" is the only significant variable in the model.
C) only months of service and gender are significantly related to monthly salary.
D) "service" is the only significant variable in the model.

Question 75

The information below is from the multiple regression analysis computer output for 28 teams in Major League Baseball. The model is designed to predict wins using attendance, payroll, batting average, home runs, stolen bases, errors, and team ERA. 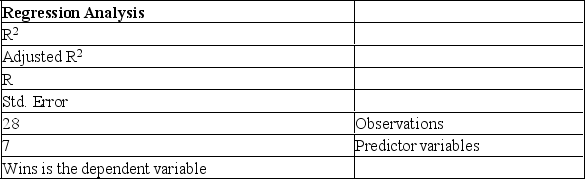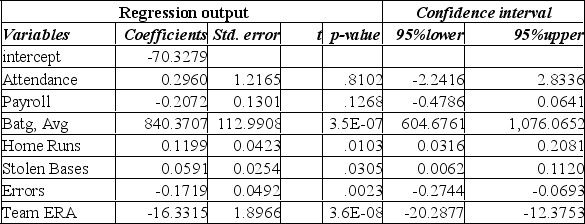The t-value computed for testing the coefficient "Batg. Avg." is:

A) 112.991.
B) 2.086.
C) 7.438.
D) 2.832.
E) -1.593.

Question 76

i. A variable whose possible outcomes are coded as a "1" or a "0" is called a dummy variable. ii. If the null hypothesis $\beta$ ₄ = 0 is not rejected, then the independent variable X₄ has no effect in predicting the dependent variable.
iii. A dummy variable is added to the regression equation to control for error.

A) (i), (ii), and (iii) are all correct statements.
B) (i) and (ii) are correct statements but not (iii).
C) (i) and (iii) are correct statements but not (ii).
D) (ii) and (iii) are correct statements but not (i).
E) (i), (ii), and (iii) are all false statements.

Question 77

Which of the following is a characteristic of the F-distribution?

A) Normally distributed
B) Positively skewed
C) Negatively skewed
D) Equal to the t-distribution

Question 78

A manager at a local bank analyzed the relationship between monthly salary and three independent variables: length of service (measured in months), gender (0 = female, 1 = male) and job type (0 = clerical, 1 = technical). The following ANOVA summarizes the regression results: 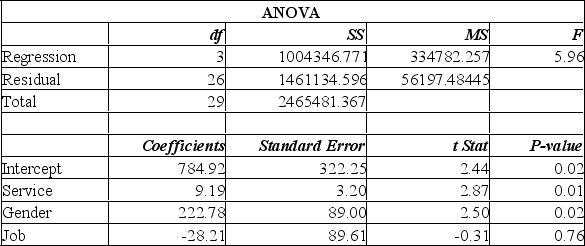The results for the variable gender show that,

A) males average $222.78 more than females in monthly salary.
B) females average $222.78 more than males in monthly salary.
C) gender is not related to monthly salary.
D) gender and months of service are correlated.

Question 79

In multiple regression, a dummy variable can be included in a multiple regression model as

A) an additional quantitative variable.
B) a nominal variable with three or more values.
C) a nominal variable with only two values.
D) a new regression coefficient.

Question 80

What can we conclude if the net regression coefficients in the population are not significantly different from zero?

A) Strong relationship exists among the variables.
B) No relationship exists between the dependent variable and the independent variables.
C) Independent variables are good predictors.
D) Good forecasts are possible.