Deck 4: Probability and Counting Rules
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/85
Play
Full screen (f)
Deck 4: Probability and Counting Rules
1
A compound event consists of two or more outcomes or simple events.
True
2
A child gets 20 heads out of 30 tosses of a coin. If he declared the chance of getting a head with that coin were 2/3, that would be an example of ____________ probability.
empirical
3
At Wassamatta University, 55.7% of the student body are males. Choose one student at random. What is the probability that the student is female?
A) 5.7%
B) 50%
C) 55.7%
D) 44.3%
A) 5.7%
B) 50%
C) 55.7%
D) 44.3%
D
4
If two dice are rolled one time, find the probability of getting a sum of 6.
A)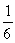
B)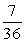
C)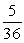
D)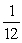
A)
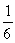
B)
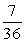
C)
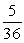
D)
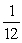

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
5
The statement, "The probability that a certain sports team will win it's next game is about 60%," is an example of
A) classical probability.
B) empirical probability.
C) subjective probability.
D) a sample space.
A) classical probability.
B) empirical probability.
C) subjective probability.
D) a sample space.

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
6
If there are 18 equally likely events, then the probability of the first one occuring is 1/18.

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
7
The staff at a small company includes: 4 secretaries, 20 technicians, 4 engineers, 2 executives, and 50 factory workers. If a person is selected at random, what is the probability that he or she is a factory worker?
A)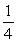
B)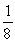
C)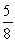
D)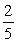
A)
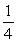
B)
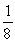
C)
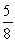
D)
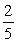

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
8
What is the set of all possible outcomes of a probability experiment?
A) an outcome
B) the sample space
C) events
D) a Venn diagram
A) an outcome
B) the sample space
C) events
D) a Venn diagram

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
9
How many possible outcomes would there be if three coins were tossed once?
A) 2
B) 4
C) 6
D) 8
A) 2
B) 4
C) 6
D) 8

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
10
If the probability that it will rain tomorrow is 0.37, what is the probability that it will not rain tomorrow?
A) 0.37
B) 0.37
0.37
C) 0.63
D) 1.37
A) 0.37
B)
 0.37
0.37C) 0.63
D) 1.37

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
11
If two dice are rolled one time, find the probability of getting a sum less than 5.
A)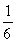
B)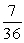
C)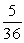
D)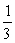
A)
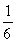
B)
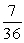
C)
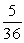
D)
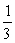

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
12
Tree diagrams are useful for
A) illustrating the law of large numbers.
B) finding all possible outcomes in a probability experiment involving several steps.
C) showing that the outcome is the set of all possible sample spaces.
D) ordering outcomes from lowest to highest.
A) illustrating the law of large numbers.
B) finding all possible outcomes in a probability experiment involving several steps.
C) showing that the outcome is the set of all possible sample spaces.
D) ordering outcomes from lowest to highest.

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
13
If a red suit is drawn from an ordinary deck of cards, what is the probability that the card is a diamond?
A)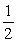
B)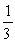
C)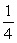
D)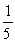
A)
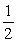
B)
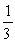
C)
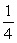
D)
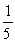

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
14
What type of probability uses a knowledge of sample spaces as opposed to experiments to determine the numerical probability that an event will occur?
A) classical probability
B) conditional probability
C) empirical probability
D) subjective probability
A) classical probability
B) conditional probability
C) empirical probability
D) subjective probability

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
15
Classical probability was the first type of probability studied formally by mathematicians of the 17th and 18th centuries.

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
16
If one tosses a coin enough times, the number of heads and tails will tend to "even out." This is an example of the law of ______________.

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
17
If a sportscaster makes an educated guess as to how well a team will do this season, he is using what type of probability?
A) classical probability
B) conditional probability
C) empirical probability
D) subjective probability
A) classical probability
B) conditional probability
C) empirical probability
D) subjective probability

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
18
If a die were rolled, the event of getting an even number would be called a simple event.

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
19
Find the probability of getting a number greater than 4 when a die is rolled one time.
A)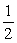
B)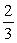
C)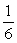
D)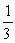
A)
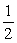
B)
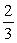
C)
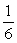
D)
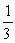

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
20
Two events are mutually exclusive if they cannot both occur.

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
21
In a recent study, the following responses were obtained to the question, "Do you favor recycling in your neighborhood?"
If a response is picked at random, what is the probability that it came from a male or that it indicated no opinion regarding recycling?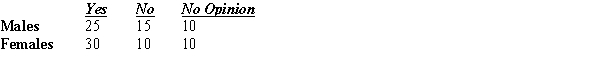
A)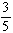
B)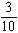
C)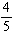
D)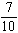
If a response is picked at random, what is the probability that it came from a male or that it indicated no opinion regarding recycling?
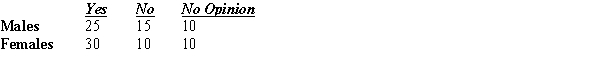
A)
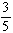
B)
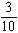
C)
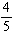
D)

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
22
If a coin is tossed three times, the probability that the coin lands on heads at least one of those three times is 7/8.

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
23
In a second grade class containing 12 girls and 9 boys, 2 students are selected at random to give out the math papers. What is the probability that both are girls?
A)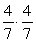
B)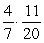
C)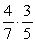
D)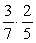
A)
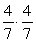
B)
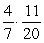
C)
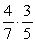
D)
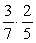

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
24
If one card is drawn from an ordinary deck of cards, what is the probability that the card will be an ace, a king of hearts, or a spade?
A)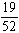
B)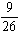
C)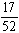
D)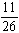
A)
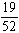
B)
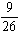
C)
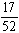
D)
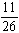

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
25
Given the following Venn diagram, which of the following equations could be used to calculate the probability of either event A, event B, or event C occurring. 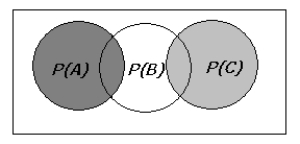
A)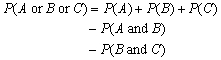
B)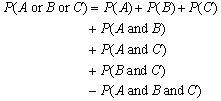
C)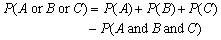
D)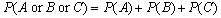

A)
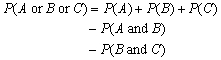
B)
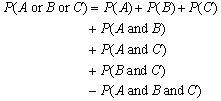
C)
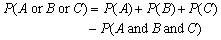
D)
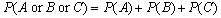

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
26
If a single card is drawn from an ordinary deck of cards, what is the probability of drawing a jack, queen, king, or ace?
A)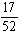
B)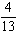
C)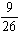
D)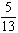
A)
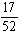
B)
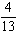
C)
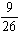
D)
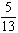

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
27
Given eight students, three of which are female, if two students are selected at random, without replacement, what is the probability that both students are female?

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
28
An apartment building has the following distribution of apartments:  If an apartment is selected at random, what is the probability that it is not a 2 bedroom apartment on the 2nd floor?
If an apartment is selected at random, what is the probability that it is not a 2 bedroom apartment on the 2nd floor?
A)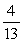
B)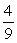
C)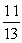
D)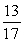
 If an apartment is selected at random, what is the probability that it is not a 2 bedroom apartment on the 2nd floor?
If an apartment is selected at random, what is the probability that it is not a 2 bedroom apartment on the 2nd floor?A)
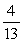
B)
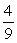
C)
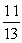
D)
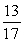

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
29
A probability experiment has two steps. There are two possible results for the first step, call them "A" and "B". If the result for the first step was "A", then there would be 4 possible results for the second step. If the result for the first step was "B", then there would be 15 possible results for the second step. How many possible outcomes are there for this experiment?
A) 60
B) 9
C) 15
D) 19
A) 60
B) 9
C) 15
D) 19

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
30
In a fish tank, there are 23 goldfish, 4 angelfish, and 9 guppies. If a fish is selected at random, find the probability that it is an angelfish or a guppy.
A)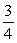
B)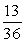
C)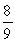
D)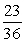
A)
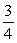
B)
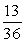
C)
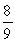
D)
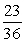

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
31
The Statistics Club at Woodvale College sold college T-shirts as a fundraiser. The results of the sale are shown below. Choose one student at random. Find the probability that the student sold 11-15 T-shirts or less than 6 T-shirts. 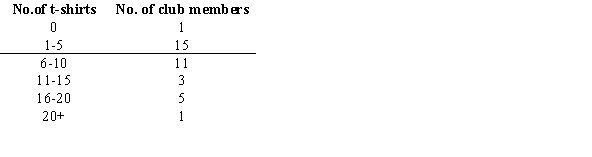
A) 0.4444
B) 0.5278
C) 0.0833
D) 0.5429
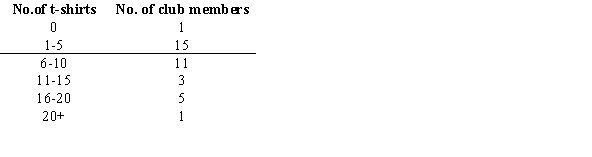
A) 0.4444
B) 0.5278
C) 0.0833
D) 0.5429

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
32
Box A contains the numbers 1, 2, 3, and 4. Box B contains the numbers 5, 6, 7, and 8. A number is first drawn from Box A and then another number from Box B. Using the figure below, how many outcomes are possible if both numbers are even? 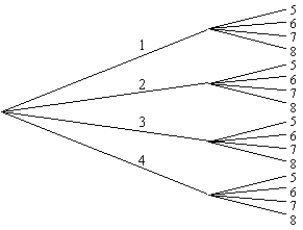
A) 16
B) 4
C) 6
D) 8

A) 16
B) 4
C) 6
D) 8

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
33
If a card is drawn from an ordinary deck of cards, and then a second card is drawn from the same deck without replacing the first card, these two events are ________________.

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
34
At a certain college, there were 600 science majors, 200 engineering majors, and 500 business majors. If one student was selected at random, the probability that the student is an engineering major is
A)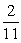
B)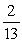
C)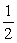
D)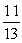
A)
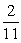
B)
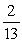
C)
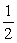
D)

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
35
A recent poll found that 30% of those surveyed are worried about aggressive drivers on the road. If three people are selected at random, what is the probability that all three will be worried about aggressive drivers on the road?
A) 0.900
B) 0.027
C) 0.081
D) 0.300
A) 0.900
B) 0.027
C) 0.081
D) 0.300

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
36
A jar contains four white marbles, five red marbles, and six black marbles. If a marble were selected at random, the probability that it is white or black would be 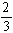 .
.
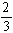 .
.
Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
37
A single card is drawn from a deck. Find the probability of selecting a heart or a 9.
A)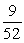
B)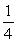
C)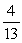
D)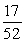
A)
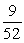
B)
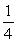
C)
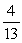
D)
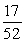

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
38
According to popular belief, 80% of adults enjoy drinking beer. Choose a group of 4 adults at random. The probability that all of them enjoy drinking beer is:
A) 0.250
B) 3.200
C) 0.200
D) 0.410
A) 0.250
B) 3.200
C) 0.200
D) 0.410

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
39
A coin is tossed 5 times. Find the probability that all 5 tosses are tails.
A)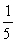
B)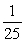
C)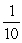
D)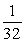
A)
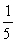
B)
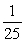
C)
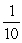
D)
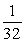

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
40
An apartment building has the following distribution of apartments:
If an apartment is selected at random, what is the probability that it is on the 2nd floor or has 2 bedrooms?
A)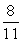
B)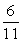
C)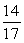
D)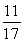
If an apartment is selected at random, what is the probability that it is on the 2nd floor or has 2 bedrooms?

A)
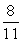
B)
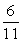
C)
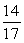
D)
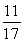

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
41
It has been reported that 3% of all cars on the highway are traveling at speeds in excess of 70 mph. If the speeds of four random automobiles are measured via radar, what is the probability that at least one car is going over 70 mph?

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
42
How many different ways can 5 brands of soda be displayed on a supermarket's shelf, one at a time in a row?
A) 10
B) 120
C) 240
D) 360
A) 10
B) 120
C) 240
D) 360

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
43
A store manager wants to display 4 different brands of toothpaste in a row. How many ways can this be done?
A) 4
B) 12
C) 6
D) 24
A) 4
B) 12
C) 6
D) 24

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
44
Urn 1 contains 6 red balls and 4 black balls. Urn 2 contains 4 red balls and 6 black balls. Urn 3 contains 4 red balls and 5 black balls. If an urn is selected at random and a ball is drawn, find the probability it will be red.
A)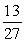
B)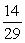
C)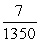
D)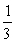
A)
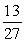
B)
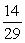
C)
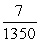
D)
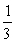

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
45
A gumball machine contains 300 grape flavored balls, 400 cherry flavored balls, and 500 lemon flavored balls. What is the probability of getting 1 grape ball, 1 cherry ball, and 1 lemon ball if each ball was removed and then replaced before choosing the next from the machine?
A) 0.0264
B) 0.0531
C) 0.0347
D) 0.0482
A) 0.0264
B) 0.0531
C) 0.0347
D) 0.0482

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
46
In the Happy Hilltop Health Home, 10% of the residents play shuffleboard, 35% of the residents play poker, and 10% of the residents garden. If 5% of the residents play poker and garden, find the probability that a resident plays poker, given that they also garden.
A) 50.0%
B) 14.3%
C) 5.6%
D) 7.7%
A) 50.0%
B) 14.3%
C) 5.6%
D) 7.7%

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
47
Below are listed the numbers of engineers in various fields by sex. Choose one engineer at random. Find 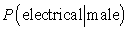 .
. 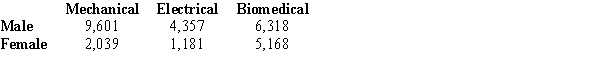
A) 0.787
B) 0.215
C) 0.152
D) 0.141
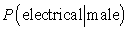 .
. 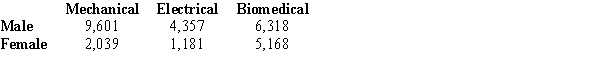
A) 0.787
B) 0.215
C) 0.152
D) 0.141

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
48
Two events A and B are ______________ if the fact that A occurs does not affect the probability of B occurring.

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
49
When the outcome of event A does not affect the probability of the outcome of a subsequent event B, then the events are said to be dependent.

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
50
In a physics class there are 10 juniors and 20 males; so there must be 30 male juniors in this class.

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
51
The ______________ probability of an event B in relationship to an event A is defined as the probability that event B occurs after event A has already occurred.

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
52
When two events are independent, the probability of both occurring is:
A)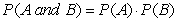
B)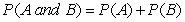
C)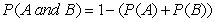
D)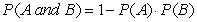
A)
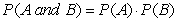
B)
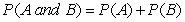
C)
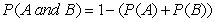
D)
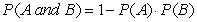

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
53
In a second grade class containing 13 girls and 9 boys, 2 students are selected at random to give out the math papers. What is the probability that the second student chosen is a boy, given that the first one was a girl?
A)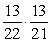
B)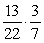
C)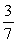
D)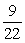
A)
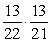
B)
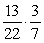
C)
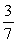
D)
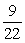

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
54
A box contains blue chips and red chips. A person selects two chips without replacement. If the probability of selecting a blue chip and a red chip is 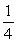 , and the probability of selecting a blue chip on the first draw is
, and the probability of selecting a blue chip on the first draw is 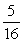 , find the probability of selecting the red chip on the second draw, given that the first chip selected was a blue chip.
, find the probability of selecting the red chip on the second draw, given that the first chip selected was a blue chip.
A)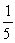
B)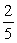
C)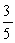
D)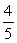
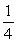 , and the probability of selecting a blue chip on the first draw is
, and the probability of selecting a blue chip on the first draw is 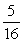 , find the probability of selecting the red chip on the second draw, given that the first chip selected was a blue chip.
, find the probability of selecting the red chip on the second draw, given that the first chip selected was a blue chip.A)
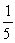
B)
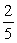
C)
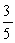
D)
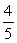

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
55
There are __________ possible ways that eight pictures can be hung along a wall.

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
56
If the letters A, B, C, D, E, and F are to be used in a five-letter code, how many different codes are possible if repetitions are not permitted?
A) 625
B) 720
C) 7,776
D) 1,296
A) 625
B) 720
C) 7,776
D) 1,296

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
57
There are 3 blue balls, 5 red balls, and 4 white balls in a bag of balls. If a person selects two of the balls, what is the probability that the second one is blue given that the first one was white?
A)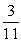
B)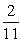
C)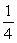
D)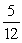
A)
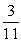
B)
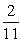
C)
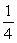
D)
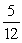

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
58
On an eight-question true-false quiz, a student guesses each answer. What is the probability that the student gets at least one of the answers correct?

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
59
A group of 10 male and 8 female students is talking about going out for pizza. If 50% of the male students actually go and 25% of the female students actually go, find the probability that a random student who goes out for pizza is female.
A)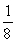
B)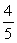
C)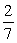
D)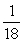
A)
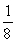
B)
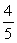
C)
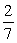
D)
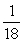

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
60
There are 3 first grade children, 5 second grade children, and 6 third grade children in a room. When choosing two children, what is the conditional probability of choosing a second grade child, given that either a first or a third grade child was chosen first?
A)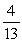
B)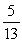
C)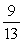
D)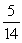
A)
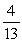
B)
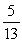
C)
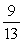
D)
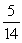

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
61
There are four instructors, nine assistant professors, and five associate professors in the Math department. A committee of five is selected to choose new textbooks. There are 1,440 ways that a committee can be selected, if there must be one instructor, two assistant professors, and two associate professors on the committee.

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
62
A business has seven locations to choose from and wishes to rank only the top three locations. How many different ways can this be done?
A) 5,040
B) 210
C) 840
D) 420
A) 5,040
B) 210
C) 840
D) 420

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
63
Evaluate the following: 7P3.
A) 210
B) 35
C) 5,040
D) 6
A) 210
B) 35
C) 5,040
D) 6

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
64
There are 3 different mathematics courses, 5 different science courses, and 2 different history courses. If a student must take one of each, how many different ways can this be done?
A) 10
B) 12
C) 30
D) 60
A) 10
B) 12
C) 30
D) 60

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
65
If a menu has a choice of 4 appetizers, 4 main courses, and 4 desserts, how many dinners are possible if each includes one appetizer, one main course, and one dessert ?
A) 64
B) 20
C) 32
D) 3
A) 64
B) 20
C) 32
D) 3

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
66
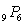 is equal to 84.
is equal to 84.
Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
67
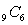 is equal to 84.
is equal to 84.
Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
68
There are 2,368 possible ways that a committee of eight people can be selected from a group of 14 people.

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
69
A club has 10 members. There are 720 ways that a chairperson, a secretary, and a treasurer can be selected from these 10 members. Assume a person can hold, at most, one office.

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
70
When a die is rolled twice, there are __________ possible outcomes.

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
71
FizzFizz soda comes in two varieties, regular and diet. If a researcher has 4 boxes of each, how many ways can he select 2 boxes of each for a quality control test?
A) 36
B) 24
C) 15
D) 8
A) 36
B) 24
C) 15
D) 8

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
72
How many different ways can four people: Andy, Betty, Cindy, and Doug, sit in a row at the opera if Andy and Betty must sit together?
A) 24
B) 12
C) 6
D) 18
A) 24
B) 12
C) 6
D) 18

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
73
A furniture manufacturer offers bookcases in 3 different sizes and 4 different colors. If every color is available in every size, then the total number of different bookcases is
A) 4
B) 7
C) 12
D) 24
A) 4
B) 7
C) 12
D) 24

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
74
Evaluate the following: 7C3.
A) 210
B) 5,040
C) 35
D) 6
A) 210
B) 5,040
C) 35
D) 6

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
75
A certain system has two components. There are 9 different models of the first component and 12 different models of the second. Any first component can be paired with any second component. A salesman must select 2 of the first component and 3 of the second to take on a sales call. How many different sets of components can the salesman take?
A)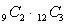
B)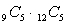
C)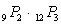
D)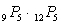
A)
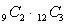
B)
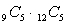
C)
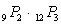
D)
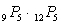

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
76
How many ways can a student select five questions from an exam containing 12 questions, if one of the five must be the last question?
A) 330
B) 7920
C) 40,320
D) 95,040
A) 330
B) 7920
C) 40,320
D) 95,040

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
77
Each of 8 students wishes to buy a particular textbook, but only 5 textbooks are available. How could one express the number of ways those textbooks could be distributed among the students?
A)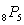
B)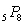
C)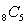
D)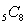
A)
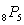
B)
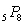
C)
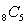
D)
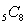

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
78
How many different ways can a teacher select 5 students from a class of 19 students to each perform a different classroom task?
A) 11,628
B) 95
C) 1,395,360
D) 240,240
A) 11,628
B) 95
C) 1,395,360
D) 240,240

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
79
The number of different arrangements of four pictures from a selection of ten pictures is 5,040.

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
80
A group of 6 children are choosing colored pencils to draw a picture. Each child is allowed to select one color. The available colors are green, red, and blue. If the second child refuses to use red pencils and the third child refuses to use blue pencils, then how many ways are there for the children to choose pencils? Assume that there are 12 pencils available of each color, and different children are allowed to choose the same color.
A) 324
B) 36
C) 729
D) 243
A) 324
B) 36
C) 729
D) 243

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck


