Deck 15: Game Theory: the Mathematics of Competition
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/113
Play
Full screen (f)
Deck 15: Game Theory: the Mathematics of Competition
1
In the following game of batter-versus-pitcher in baseball, the batter's batting averages are shown in the game matrix:  Solve the game determining the best mix of selections for both batter and pitcher.
Solve the game determining the best mix of selections for both batter and pitcher.
 Solve the game determining the best mix of selections for both batter and pitcher.
Solve the game determining the best mix of selections for both batter and pitcher.Batter always expects fastball. Pitcher always plays knuckleball.
2
Describe a saddlepoint of a zero-sum game for two players where the payoff matrix represent gains to the row player I and losses to column player II.
When the maximum of row minimums is equal to the minimum of column maximums, the resulting payoff is called a saddlepoint and the value of the game.
3
In the following game of batter-versus-pitcher in baseball, the batter's batting averages are shown in the game matrix:  Solve the game, determining the best mix of selections for both batter and pitcher.
Solve the game, determining the best mix of selections for both batter and pitcher.
 Solve the game, determining the best mix of selections for both batter and pitcher.
Solve the game, determining the best mix of selections for both batter and pitcher.Batter expects 3/4 knuckleball and 1/4 fastball. Pitcher plays 3/4 knuckleball and 1/4 fastball.
4
Describe a payoff matrix of a two-person total-conflict game.

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
5
Create a three-by-three matrix that represents a two-person zero-sum game in which each player has three options and the game has a saddlepoint.

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
6
In the game of matching pennies, player I wins a penny if the coins match and player II wins if the coins do not match. Is this a zero-sum game? Is this a fair game?

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
7
Create a three-by-three matrix that represents a two-person zero-sum game in which each player has three options and the game has no saddlepoint.

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
8
In the following two-person zero-sum game, the payoffs represent gains to the row player I and losses to column player II.  Does this game have a saddlepoint? What is each player's minimax or maximin strategy? Justify your response.
Does this game have a saddlepoint? What is each player's minimax or maximin strategy? Justify your response.
 Does this game have a saddlepoint? What is each player's minimax or maximin strategy? Justify your response.
Does this game have a saddlepoint? What is each player's minimax or maximin strategy? Justify your response.
Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
9
Create a three-by-three matrix that represents a two-person zero-sum game in which each player has three options and at least one player has a dominated strategy.

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
10
You want to carry insurance for your small business. The annual policy costs $1000 this year. If you are sued and you have no insurance, you will pay $5000. If you have insurance and are sued you pay nothing, and your partner gives you $500 for your wise foresight, so that the policy costs you only $500. Represent this game as a two-by-two matrix.

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
11
In the following game of batter-versus-pitcher in baseball, the batter's batting averages are shown in the game matrix:  Solve the game determining the best mix of selections for both batter and pitcher.
Solve the game determining the best mix of selections for both batter and pitcher.
 Solve the game determining the best mix of selections for both batter and pitcher.
Solve the game determining the best mix of selections for both batter and pitcher.
Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
12
In a game, each player chooses one of three coins: penny, nickel, or dime. If both players choose the same coin, both players loose their coin. Otherwise, the player with the more valuable coin wins the less valuable coin from the other player. Represent this game as a three-by-three matrix of ordered pairs.

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
13
In the game of matching pennies, player I wins a penny if the coins match and player II wins if the coins do not match. Present this game as a two-by-two matrix, where each player has two outcomes from which to select.

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
14
In the following two-person zero-sum game, the payoffs represent gains to the row player I and losses to column player II.  Does this game have a saddlepoint? What is each player's minimax or maximin strategy? Justify your response.
Does this game have a saddlepoint? What is each player's minimax or maximin strategy? Justify your response.
 Does this game have a saddlepoint? What is each player's minimax or maximin strategy? Justify your response.
Does this game have a saddlepoint? What is each player's minimax or maximin strategy? Justify your response.
Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
15
Describe a Nash equilibrium.

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
16
In the following two-person zero-sum game, the payoffs represent gains to the row player I and losses to column player II.  Does this game have a saddlepoint? What is each player's minimax or maximin strategy? Justify your response.
Does this game have a saddlepoint? What is each player's minimax or maximin strategy? Justify your response.
 Does this game have a saddlepoint? What is each player's minimax or maximin strategy? Justify your response.
Does this game have a saddlepoint? What is each player's minimax or maximin strategy? Justify your response.
Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
17
In the following two-person zero-sum game, the payoffs represent gains to the row player I and losses to column player II.  Does this game have a saddlepoint? What is each player's minimax or maximin strategy? Justify your response.
Does this game have a saddlepoint? What is each player's minimax or maximin strategy? Justify your response.
 Does this game have a saddlepoint? What is each player's minimax or maximin strategy? Justify your response.
Does this game have a saddlepoint? What is each player's minimax or maximin strategy? Justify your response.
Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
18
In the following two-person zero-sum game, the payoffs represent gains to the row player I and losses to column player II.  Does this game have a saddlepoint? What is each player's minimax or maximin strategy? Justify your response.
Does this game have a saddlepoint? What is each player's minimax or maximin strategy? Justify your response.
 Does this game have a saddlepoint? What is each player's minimax or maximin strategy? Justify your response.
Does this game have a saddlepoint? What is each player's minimax or maximin strategy? Justify your response.
Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
19
Describe a zero-sum game.

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
20
In the following two-person zero-sum game, the payoffs represent gains to the row player I and losses to column player II.  Does this game have a saddlepoint? What is each player's minimax or maximin strategy? Justify your response.
Does this game have a saddlepoint? What is each player's minimax or maximin strategy? Justify your response.
 Does this game have a saddlepoint? What is each player's minimax or maximin strategy? Justify your response.
Does this game have a saddlepoint? What is each player's minimax or maximin strategy? Justify your response.
Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
21
Use the following information to answer Questions
In American football the "third down and short" situation occurs often. The probabilities of obtaining a first down, shown below, are dependent on the choice of the offense and the anticipated choice of the defense.
Suppose the value of the game is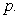 What does this mean for the offense?
What does this mean for the offense?
In American football the "third down and short" situation occurs often. The probabilities of obtaining a first down, shown below, are dependent on the choice of the offense and the anticipated choice of the defense.

Suppose the value of the game is
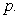 What does this mean for the offense?
What does this mean for the offense?
Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
22
Construct the game tree for a truel played sequentially, for which the outcomes have the following payoffs. What are the optimal strategies for this game? 


Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
23
Consider the following partial-conflict game played in a noncooperative manner. The first payoff is to player I; the second is to player II.  Discuss the players' possible strategies when this game is played.
Discuss the players' possible strategies when this game is played.
 Discuss the players' possible strategies when this game is played.
Discuss the players' possible strategies when this game is played.
Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
24
In the following two-person zero-sum game, the payoffs represent gains to the row player I and losses to the column player II. Does this game have a saddlepoint? What is each player's minimax or maximin strategy? 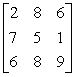


Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
25
The minimax strategy of a column player is the strategy that corresponds to the minimum value of the maximum numbers in the columns.

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
26
If you cheat on your income tax return you will pay $1000 in taxes; if you don't cheat you will pay $2000. If you are audited and you didn't cheat, your auditor will be kind and reduce your taxes from $2000 to $1500. If you are audited and you did cheat, you will be caught and have to pay a total of $2500, including penalties. Statistically, how often should the government audit you?

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
27
Construct the game tree for a truel played sequentially, for which the outcomes have the following payoffs. What are the optimal strategies for this game? 


Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
28
If you cheat on your income tax return you will pay $1000 in taxes; if you don't cheat you will pay $2000. If you are audited and you didn't cheat, your auditor will be kind and reduce your taxes from $2000 to $1500. If you are audited and you did cheat, you will be caught and have to pay a total of $2500, including penalties. Statistically, how often should you cheat?

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
29
Describe a Nash equilibrium in a Vickrey auction.

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
30
A total-conflict game is a zero-sum game.

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
31
Construct the game tree for a truel played sequentially, for which the outcomes have the following payoffs. What are the optimal strategies for this game? 


Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
32
Use the following information to answer Questions
In American football the "third down and short" situation occurs often. The probabilities of obtaining a first down, shown below, are dependent on the choice of the offense and the anticipated choice of the defense.
What is the optimal mixed strategy for the defense?
In American football the "third down and short" situation occurs often. The probabilities of obtaining a first down, shown below, are dependent on the choice of the offense and the anticipated choice of the defense.

What is the optimal mixed strategy for the defense?

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
33
In the following two-person zero-sum game, the payoffs represent gains to the row player I and losses to the column player II. Does this game have a saddlepoint? What is each player's minimax or maximin strategy? 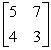


Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
34
Use the following information to answer Questions
In American football the "third down and short" situation occurs often. The probabilities of obtaining a first down, shown below, are dependent on the choice of the offense and the anticipated choice of the defense.
Suppose the value of the game is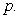 What does this mean for the defense?
What does this mean for the defense?
In American football the "third down and short" situation occurs often. The probabilities of obtaining a first down, shown below, are dependent on the choice of the offense and the anticipated choice of the defense.

Suppose the value of the game is
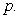 What does this mean for the defense?
What does this mean for the defense?
Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
35
Consider the following partial-conflict game played in a noncooperative manner. The first payoff is to player I; the second to player II. 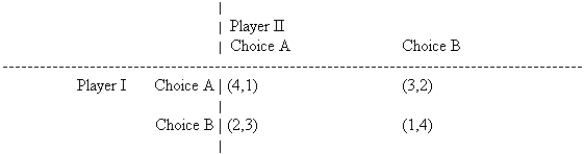 Discuss the players' possible strategies when this game is played.
Discuss the players' possible strategies when this game is played.
 Discuss the players' possible strategies when this game is played.
Discuss the players' possible strategies when this game is played.
Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
36
Use the following information to answer Questions
In American football the "third down and short" situation occurs often. The probabilities of obtaining a first down, shown below, are dependent on the choice of the offense and the anticipated choice of the defense.
What is the optimal mixed strategy for the offense?
In American football the "third down and short" situation occurs often. The probabilities of obtaining a first down, shown below, are dependent on the choice of the offense and the anticipated choice of the defense.

What is the optimal mixed strategy for the offense?

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
37
Consider the following partial-conflict game played in a noncooperative manner. The first payoff is to player I; the second is to player II.  Discuss the players' possible strategies when this game is played.
Discuss the players' possible strategies when this game is played.
 Discuss the players' possible strategies when this game is played.
Discuss the players' possible strategies when this game is played.
Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
38
What is the name of a table whose rows and columns correspond to the strategies of the two players?
A) strategy matrix
B) payoff matrix
C) value matrix
D) profit matrix
A) strategy matrix
B) payoff matrix
C) value matrix
D) profit matrix

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
39
In the following two-person zero-sum game, the payoffs represent gains to the row player I and losses to the column player II. Does this game have a saddlepoint? What is each player's minimax or maximin strategy? 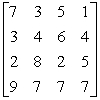


Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
40
Use the following information to answer Questions
In American football the "third down and short" situation occurs often. The probabilities of obtaining a first down, shown below, are dependent on the choice of the offense and the anticipated choice of the defense.
What is the value of the game
In American football the "third down and short" situation occurs often. The probabilities of obtaining a first down, shown below, are dependent on the choice of the offense and the anticipated choice of the defense.

What is the value of the game

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
41
In the following two-person zero-sum game, the payoffs represent gains to the row player I and losses to column player II.  The minimax strategy of player II is:
The minimax strategy of player II is:
A) to always play the first column.
B) to always play the second column.
C) to always play the third column.
D) to always play the fourth column.
 The minimax strategy of player II is:
The minimax strategy of player II is:A) to always play the first column.
B) to always play the second column.
C) to always play the third column.
D) to always play the fourth column.

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
42
In the following two-person zero-sum game, the payoffs represent gains to the row player I and losses to column player II.  The minimax strategy of player II is:
The minimax strategy of player II is:
A) to always play the first column.
B) to always play the second column.
C) to always play the third column.
D) to play two or more of the columns.
 The minimax strategy of player II is:
The minimax strategy of player II is:A) to always play the first column.
B) to always play the second column.
C) to always play the third column.
D) to play two or more of the columns.

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
43
In the following two-person zero-sum game, the payoffs represent gains to the row player I and losses to column player II.  The maximin strategy of player I is:
The maximin strategy of player I is:
A) to always play the first row.
B) to always play the second row.
C) to always play the third row.
D) to always play the fourth row.
 The maximin strategy of player I is:
The maximin strategy of player I is:A) to always play the first row.
B) to always play the second row.
C) to always play the third row.
D) to always play the fourth row.

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
44
The value of a zero-sum game is a saddlepoint.

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
45
In the following two-person zero-sum game, the payoffs represent gains to the row player I and losses to column player II. 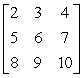 Which of the following statements is true?
Which of the following statements is true?
A) The game has no saddlepoint.
B) There is a saddlepoint at row 1, column 1.
C) There is a saddlepoint at row 3, column 1.
D) There is a saddlepoint at row 3, column 3.
 Which of the following statements is true?
Which of the following statements is true?A) The game has no saddlepoint.
B) There is a saddlepoint at row 1, column 1.
C) There is a saddlepoint at row 3, column 1.
D) There is a saddlepoint at row 3, column 3.

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
46
In the following two-person zero-sum game, the payoffs represent gains to the row player I and losses to column player II.  Which of the following statements is true?
Which of the following statements is true?
A) The game has no saddlepoint.
B) The game has a saddlepoint; the value of the game is 4.
C) The game has a saddlepoint; the value of the game is 5.
D) The game has a saddlepoint; the value of the game is 6.
 Which of the following statements is true?
Which of the following statements is true?A) The game has no saddlepoint.
B) The game has a saddlepoint; the value of the game is 4.
C) The game has a saddlepoint; the value of the game is 5.
D) The game has a saddlepoint; the value of the game is 6.

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
47
In the following two-person zero-sum game, the payoffs represent gains to the row player I and losses to column player II. 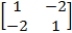 Which of the following statements is true?
Which of the following statements is true?
A) The game has no saddlepoint.
B) There is a saddlepoint at row 2, column 2.
C) There is a saddlepoint at row 2, column 1.
D) There is a saddlepoint at row 1, column 2.
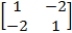 Which of the following statements is true?
Which of the following statements is true?A) The game has no saddlepoint.
B) There is a saddlepoint at row 2, column 2.
C) There is a saddlepoint at row 2, column 1.
D) There is a saddlepoint at row 1, column 2.

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
48
In the following two-person zero-sum game, the payoffs represent gains to the row player I and losses to column player II.  Which of the following statements is true?
Which of the following statements is true?
A) The maximin strategy of player I is to always play the first row; the minimax strategy of player II is to always play the first column.
B) The maximin strategy of player I is to always play the second row; the minimax strategy of player II is to always play the first column.
C) The maximin strategy of player I is to always play the first row; the minimax strategy of player II is to always play the second column.
D) The maximin strategy of player I is to always play the second row; the minimax strategy of player II is to always play the second column.
 Which of the following statements is true?
Which of the following statements is true?A) The maximin strategy of player I is to always play the first row; the minimax strategy of player II is to always play the first column.
B) The maximin strategy of player I is to always play the second row; the minimax strategy of player II is to always play the first column.
C) The maximin strategy of player I is to always play the first row; the minimax strategy of player II is to always play the second column.
D) The maximin strategy of player I is to always play the second row; the minimax strategy of player II is to always play the second column.

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
49
In the following game of batter-versus-pitcher in baseball, the batter's batting averages are shown in the game matrix.  Which of the following statements is true?
Which of the following statements is true?
A) The game has no saddlepoint.
B) The game has a saddlepoint; the value of the game is .200.
C) The game has a saddlepoint; the value of the game is .300.
D) The game has a saddlepoint; the value of the game is .400.
 Which of the following statements is true?
Which of the following statements is true?A) The game has no saddlepoint.
B) The game has a saddlepoint; the value of the game is .200.
C) The game has a saddlepoint; the value of the game is .300.
D) The game has a saddlepoint; the value of the game is .400.

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
50
In the following two-person zero-sum game, the payoffs represent gains to the row player I and losses to column player II. 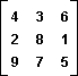 The maximin strategy of player I is:
The maximin strategy of player I is:
A) to always play the first row.
B) to always play the second row.
C) to always play the third row.
D) to play two or more of the rows.
 The maximin strategy of player I is:
The maximin strategy of player I is:A) to always play the first row.
B) to always play the second row.
C) to always play the third row.
D) to play two or more of the rows.

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
51
In the following two-person zero-sum game, the payoffs represent gains to the row player I and losses to column player II. 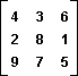 The minimax strategy of player II is:
The minimax strategy of player II is:
A) to always play the first column.
B) to always play the second column.
C) to always play the third column.
D) to play two or more of the columns.
 The minimax strategy of player II is:
The minimax strategy of player II is:A) to always play the first column.
B) to always play the second column.
C) to always play the third column.
D) to play two or more of the columns.

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
52
In the following two-person zero-sum game, the payoffs represent gains to the row player I and losses to column player II.  The maximin strategy of player I is:
The maximin strategy of player I is:
A) to always play the first row.
B) to always play the second row.
C) to always play the third row.
D) to play two or more of the rows.
 The maximin strategy of player I is:
The maximin strategy of player I is:A) to always play the first row.
B) to always play the second row.
C) to always play the third row.
D) to play two or more of the rows.

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
53
In the following two-person zero-sum game, the payoffs represent gains to the row player I and losses to column player II.  The maximin strategy of player I is:
The maximin strategy of player I is:
A) to always play the first row.
B) to always play the second row.
C) to always play the third row.
D) to always play the fourth row.
 The maximin strategy of player I is:
The maximin strategy of player I is:A) to always play the first row.
B) to always play the second row.
C) to always play the third row.
D) to always play the fourth row.

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
54
In the following two-person zero-sum game, the payoffs represent gains to the row player I and losses to column player II.  Which of the following statements is true?
Which of the following statements is true?
A) The game has no saddlepoint.
B) The game has a saddlepoint; the value of the game is 8.
C) The game has a saddlepoint; the value of the game is 9.
D) The game has a saddlepoint; the value of the game is 11.
 Which of the following statements is true?
Which of the following statements is true?A) The game has no saddlepoint.
B) The game has a saddlepoint; the value of the game is 8.
C) The game has a saddlepoint; the value of the game is 9.
D) The game has a saddlepoint; the value of the game is 11.

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
55
In the following two-person zero-sum game, the payoffs represent gains to the row player I and losses to column player II.  Which of the following statements is true?
Which of the following statements is true?
A) The maximin strategy of player I is to always play the first row; the minimax strategy of player II is to always play the first column.
B) The maximin strategy of player I is to always play the second row; the minimax strategy of player II is to always play the first column.
C) The maximin strategy of player I is to always play the first row; the minimax strategy of player II is to always play the second column.
D) The maximin strategy of player I is to always play the second row; the minimax strategy of player II is to always play the second column.
 Which of the following statements is true?
Which of the following statements is true?A) The maximin strategy of player I is to always play the first row; the minimax strategy of player II is to always play the first column.
B) The maximin strategy of player I is to always play the second row; the minimax strategy of player II is to always play the first column.
C) The maximin strategy of player I is to always play the first row; the minimax strategy of player II is to always play the second column.
D) The maximin strategy of player I is to always play the second row; the minimax strategy of player II is to always play the second column.

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
56
In the following two-person zero-sum game, the payoffs represent gains to the row player I and losses to column player II.  The minimax strategy of player II is:
The minimax strategy of player II is:
A) to always play the first column.
B) to always play the second column.
C) to always play the third column.
D) to always play the fourth column.
 The minimax strategy of player II is:
The minimax strategy of player II is:A) to always play the first column.
B) to always play the second column.
C) to always play the third column.
D) to always play the fourth column.

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
57
In the following two-person zero-sum game, the payoffs represent gains to the row player I and losses to column player II. 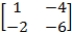 Which of the following statements is true?
Which of the following statements is true?
A) The game has no saddlepoint.
B) There is a saddlepoint at row 2, column 2.
C) There is a saddlepoint at row 2, column 1.
D) There is a saddlepoint at row 1, column 2.
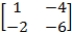 Which of the following statements is true?
Which of the following statements is true?A) The game has no saddlepoint.
B) There is a saddlepoint at row 2, column 2.
C) There is a saddlepoint at row 2, column 1.
D) There is a saddlepoint at row 1, column 2.

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
58
In the following two-person zero-sum game, the payoffs represent gains to the row player I and losses to column player II.  The maximin strategy of player I is:
The maximin strategy of player I is:
A) to always play the first row.
B) to always play the second row.
C) to always play the third row.
D) to play two or more of the rows.
 The maximin strategy of player I is:
The maximin strategy of player I is:A) to always play the first row.
B) to always play the second row.
C) to always play the third row.
D) to play two or more of the rows.

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
59
In the following two-person zero-sum game, the payoffs represent gains to the row player I and losses to column player II.  The minimax strategy of player II is:
The minimax strategy of player II is:
A) to always play the first column.
B) to always play the second column.
C) to always play the third column.
D) to play two or more of the columns.
 The minimax strategy of player II is:
The minimax strategy of player II is:A) to always play the first column.
B) to always play the second column.
C) to always play the third column.
D) to play two or more of the columns.

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
60
In the following two-person zero-sum game, the payoffs represent gains to the row player I and losses to column player II.  Which of the following statements is true?
Which of the following statements is true?
A) The game has no saddlepoint.
B) The game has a saddlepoint; the value of the game is 8.
C) The game has a saddlepoint; the value of the game is 9.
D) The game has a saddlepoint; the value of the game is 11.
 Which of the following statements is true?
Which of the following statements is true?A) The game has no saddlepoint.
B) The game has a saddlepoint; the value of the game is 8.
C) The game has a saddlepoint; the value of the game is 9.
D) The game has a saddlepoint; the value of the game is 11.

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
61
Use the following information to answer Questions 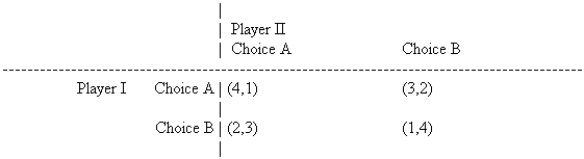
Which of the following statements is true?
A) Both player I and player II have dominant strategies.
B) Neither player I nor II has a dominant strategy.
C) Only player I has a dominant strategy.
D) Only player II has a dominant strategy.

Which of the following statements is true?
A) Both player I and player II have dominant strategies.
B) Neither player I nor II has a dominant strategy.
C) Only player I has a dominant strategy.
D) Only player II has a dominant strategy.

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
62
In the following game of batter-versus-pitcher in baseball, the batter's batting averages are shown in the game matrix.  What is the pitcher's optimal strategy?
What is the pitcher's optimal strategy?
A) Pitch more fastballs than curves.
B) Pitch more curves than fastballs.
C) Pitch fastballs and curves equally.
 What is the pitcher's optimal strategy?
What is the pitcher's optimal strategy?A) Pitch more fastballs than curves.
B) Pitch more curves than fastballs.
C) Pitch fastballs and curves equally.

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
63
As the buyer for your business, you can choose to buy an extended warranty for each new computer for $200 each. During this period, each computer will experience either a minor ($100) or major ($500) repair bill. Repairs for each computer under warranty are reduced by 50% to $50 or $250. Assume the computer company wants to make as much money as possible, and you wish to spend as little as possible. What is your optimal strategy?
A) Never buy the warranty.
B) Always buy the warranty.
C) Buy the warranty for less than half of the computers.
D) Buy the warranty for more than half of the computers.
A) Never buy the warranty.
B) Always buy the warranty.
C) Buy the warranty for less than half of the computers.
D) Buy the warranty for more than half of the computers.

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
64
Use the following information to answer Questions The probabilities of obtaining a first down, shown below, are dependent on the choice of the offense and the anticipated choice of the defense.
-In such situations, what is the optimal solution for the defense?
A) always anticipate a run
B) always anticipate a pass
C) play the mixed strategy
D) play the mixed strategy
-In such situations, what is the optimal solution for the defense?
A) always anticipate a run
B) always anticipate a pass
C) play the mixed strategy
D) play the mixed strategy

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
65
Use the following information to answer Questions The probabilities of obtaining a first down, shown below, are dependent on the choice of the offense and the anticipated choice of the defense.
-What is the value of the game?
A)
B)
C)
D)
-What is the value of the game?
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
66
Use the following information to answer Questions The probabilities of obtaining a first down, shown below, are dependent on the choice of the offense and the anticipated choice of the defense.
-In such situations, what is the optimal solution for the offense?
A) always run
B) always pass
C) play the mixed strategy
D) play the mixed strategy
-In such situations, what is the optimal solution for the offense?
A) always run
B) always pass
C) play the mixed strategy
D) play the mixed strategy

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
67
You are considering cheating on your income tax return. If you cheat you will pay $1000 in taxes; if you don't cheat you will pay $2000. If you are audited and you didn't cheat, your auditor will be kind and reduce your taxes from $2000 to $1500. If you are audited and you did cheat, you will be caught and have to pay a total of $2500, including penalties. Statistically, which is the best option for you to choose?
A) definitely cheat
B) probably cheat
C) probably don't cheat
D) definitely don't cheat
A) definitely cheat
B) probably cheat
C) probably don't cheat
D) definitely don't cheat

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
68
You can choose to buy an extended warranty for your computer for $200. During this period, you will experience either a minor ($100) or major ($500) repair bill. If you buy the warranty, you will not have to pay the repair bill. Assume the company wants to make as much money as possible, and you wish to spend as little as possible. Which of the following is a true statement?
A) This game has no saddlepoint.
B) This game has a saddlepoint; the value of the game is $100.
C) This game has a saddlepoint; the value of the game is $200.
D) This game has a saddlepoint; the value of the game is $500.
A) This game has no saddlepoint.
B) This game has a saddlepoint; the value of the game is $100.
C) This game has a saddlepoint; the value of the game is $200.
D) This game has a saddlepoint; the value of the game is $500.

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
69
In the following game of batter-versus-pitcher in baseball, the batter's batting averages are shown in the game matrix. 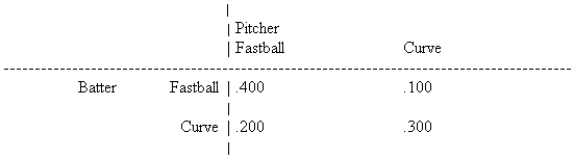 What is the pitcher's optimal strategy?
What is the pitcher's optimal strategy?
A) Pitch more fastballs than curves.
B) Pitch more curves than fastballs.
C) Pitch fastballs and curves equally.
 What is the pitcher's optimal strategy?
What is the pitcher's optimal strategy?A) Pitch more fastballs than curves.
B) Pitch more curves than fastballs.
C) Pitch fastballs and curves equally.

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
70
In American football the "third down and short" situation occurs often. The probabilities of obtaining a first down, shown below, are dependent on the choice of the offense and the anticipated choice of the defense.  In such situations, what is the optimal solution for the defense?
In such situations, what is the optimal solution for the defense?
A) always anticipate a run
B) always anticipate a pass
C) anticipate a run more often than a pass
D) anticipate a pass more often than a run
 In such situations, what is the optimal solution for the defense?
In such situations, what is the optimal solution for the defense?A) always anticipate a run
B) always anticipate a pass
C) anticipate a run more often than a pass
D) anticipate a pass more often than a run

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
71
As the buyer for your business, you can choose to buy an extended warranty for each new computer for $200 each. During this period, each computer will experience either a minor ($100) or major ($500) repair bill. Repairs for each computer under warranty are reduced by 50% to $50 or $250. Assume the computer company wants to make as much money as possible, and you wish to spend as little as possible. What is the computer company's optimal strategy?
A) Always sell the warranty.
B) Never sell the warranty.
C) Sell the warranty for less than half of the computers.
D) Sell the warranty for more than half of the computers.
A) Always sell the warranty.
B) Never sell the warranty.
C) Sell the warranty for less than half of the computers.
D) Sell the warranty for more than half of the computers.

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
72
In the following game of batter-versus-pitcher in baseball, the batter's batting averages are shown in the game matrix.  What is the batter's optimal strategy?
What is the batter's optimal strategy?
A) Expect more fastballs than curves.
B) Expect more curves than fastballs.
C) Expect equal numbers of curves and fastballs.
 What is the batter's optimal strategy?
What is the batter's optimal strategy?A) Expect more fastballs than curves.
B) Expect more curves than fastballs.
C) Expect equal numbers of curves and fastballs.

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
73
In American football the "third down and short" situation occurs often. The probabilities of obtaining a first down, shown below, are dependent on the choice of the offense and the anticipated choice of the defense.  In such situations, what is the optimal solution for the offense? a) always choose to run
In such situations, what is the optimal solution for the offense? a) always choose to run
B) always choose to pass
C) choose to run more often than pass
D) choose to pass more often than run
 In such situations, what is the optimal solution for the offense? a) always choose to run
In such situations, what is the optimal solution for the offense? a) always choose to runB) always choose to pass
C) choose to run more often than pass
D) choose to pass more often than run

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
74
Consider the following partial-conflict game played in a noncooperative manner. 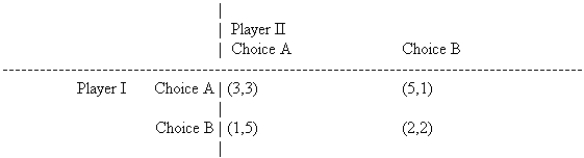 What outcomes constitute a Nash equilibrium?
What outcomes constitute a Nash equilibrium?
A) only when both players select choice A
B) only when both players select choice B
C) only when one player selects choice A; the other selects choice B
D) only when both players select choice A or both players select choice B
 What outcomes constitute a Nash equilibrium?
What outcomes constitute a Nash equilibrium?A) only when both players select choice A
B) only when both players select choice B
C) only when one player selects choice A; the other selects choice B
D) only when both players select choice A or both players select choice B

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
75
Use the following information to answer Questions 
Which of the following is a Nash equilibrium?
A) Player I selects choice A; player II selects choice A.
B) Player I selects choice A; player II selects choice B.
C) Player I selects choice B; player II selects choice A.
D) Player I selects choice B; player II selects choice B.

Which of the following is a Nash equilibrium?
A) Player I selects choice A; player II selects choice A.
B) Player I selects choice A; player II selects choice B.
C) Player I selects choice B; player II selects choice A.
D) Player I selects choice B; player II selects choice B.

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
76
In the following game of batter-versus-pitcher in baseball, the batter's batting averages are shown in the game matrix. 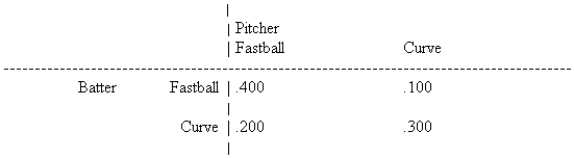 What is the batter's optimal strategy?
What is the batter's optimal strategy?
A) Expect more fastballs than curves.
B) Expect more curves than fastballs.
C) Expect equal numbers of curves and fastballs.
 What is the batter's optimal strategy?
What is the batter's optimal strategy?A) Expect more fastballs than curves.
B) Expect more curves than fastballs.
C) Expect equal numbers of curves and fastballs.

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
77
You can choose to buy an extended warranty for your computer for $200. During this period, you will experience either a minor ($100) or major ($500) repair bill. If you buy the warranty, you pay 50% of any repair bill: that is, you will pay either $50 or $250 for the subsequent repair. Assume the company wants to make as much money as possible, and you wish to spend as little as possible. Which of the following is a true statement?
A) This game has no saddlepoint.
B) This game has a saddlepoint; the value of the game is $200.
C) This game has a saddlepoint; the value of the game is $250.
D) This game has a saddlepoint; the value of the game is $450.
A) This game has no saddlepoint.
B) This game has a saddlepoint; the value of the game is $200.
C) This game has a saddlepoint; the value of the game is $250.
D) This game has a saddlepoint; the value of the game is $450.

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
78
If you cheat on your income tax return you will pay $1000 in taxes; if you don't cheat you will pay $2000. If you are audited and you didn't cheat, your auditor will be kind and reduce your taxes from $2000 to $1500. If you are audited and you did cheat, you will be caught and have to pay a total of $2500, including penalties. Assuming the government wants to receive as much money as possible, statistically, which is the best option for the government to choose?
A) always audit
B) usually audit
C) occasionally audit
D) never audit
A) always audit
B) usually audit
C) occasionally audit
D) never audit

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
79
Consider the following partial-conflict game played in a noncooperative manner. 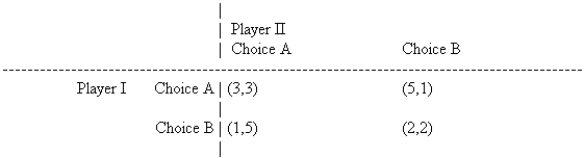 Which of the following statements is true?
Which of the following statements is true?
A) The dominant strategy for player I is to select choice A.
B) The dominant strategy for player I is to select choice B.
C) Player I has no dominant strategy.
 Which of the following statements is true?
Which of the following statements is true?A) The dominant strategy for player I is to select choice A.
B) The dominant strategy for player I is to select choice B.
C) Player I has no dominant strategy.

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
80
In the following game of batter-versus-pitcher in baseball, the batter's batting averages are shown in the game matrix. 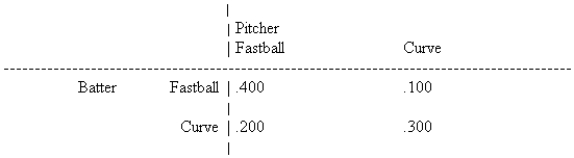 Which of the following statements is true?
Which of the following statements is true?
A) The game has no saddlepoint.
B) The game has a saddlepoint; the value of the game is .200.
C) The game has a saddlepoint; the value of the game is .300.
D) The game has a saddlepoint; the value of the game is .400.
 Which of the following statements is true?
Which of the following statements is true?A) The game has no saddlepoint.
B) The game has a saddlepoint; the value of the game is .200.
C) The game has a saddlepoint; the value of the game is .300.
D) The game has a saddlepoint; the value of the game is .400.

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck


