Deck 14: Apportionment
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/112
Play
Full screen (f)
Deck 14: Apportionment
1
Explain the population paradox.
The population paradox occurs when one state's apportionment decreases and another state's apportionment increases even though the first state has gained population and the second state has lost population.
2
Use the Jefferson method of apportionment to distribute 15 representatives to the three states with the populations shown below. 

A 8
B 5
C 2
B 5
C 2
3
Given the cities and the populations below, use the Webster method of apportionment to distribute 25 seats on a regional board. 

Greenville 9
Riverdale 7
Oceanside 5
Parkview 4
Riverdale 7
Oceanside 5
Parkview 4
4
Explain the new state paradox.

Unlock Deck
Unlock for access to all 112 flashcards in this deck.
Unlock Deck
k this deck
5
Use the Hamilton method of apportionment to distribute 12 seats on a city council to three districts with the populations shown below. 


Unlock Deck
Unlock for access to all 112 flashcards in this deck.
Unlock Deck
k this deck
6
Use the following information to answer Questions 5-7.
A city is divided into three regions for distributing the 20 representatives on a public utility board. The regions and their populations are shown below.
Compute the quota for each region.
A city is divided into three regions for distributing the 20 representatives on a public utility board. The regions and their populations are shown below.

Compute the quota for each region.

Unlock Deck
Unlock for access to all 112 flashcards in this deck.
Unlock Deck
k this deck
7
Use the Webster method of apportionment to distribute 12 seats on a city council to three districts with the populations shown below. 


Unlock Deck
Unlock for access to all 112 flashcards in this deck.
Unlock Deck
k this deck
8
Given the cities and the populations below, use the Jefferson method of apportionment to distribute 25 seats on a regional board. 


Unlock Deck
Unlock for access to all 112 flashcards in this deck.
Unlock Deck
k this deck
9
A city is divided into four regions for distributing the 20 representatives on a public utility board. The regions and their populations are shown below. The board uses the Hamilton method of apportionment to distribute seats. Find the district population for each region based on this apportionment. 


Unlock Deck
Unlock for access to all 112 flashcards in this deck.
Unlock Deck
k this deck
10
Explain the Alabama paradox.

Unlock Deck
Unlock for access to all 112 flashcards in this deck.
Unlock Deck
k this deck
11
Use the Jefferson method of apportionment to distribute representatives.

Unlock Deck
Unlock for access to all 112 flashcards in this deck.
Unlock Deck
k this deck
12
Given the cities and the populations below, use the Hamilton method of apportionment to distribute 25 seats on a regional board. 


Unlock Deck
Unlock for access to all 112 flashcards in this deck.
Unlock Deck
k this deck
13
Use the Jefferson method of apportionment to distribute 12 seats on a city council to three districts with the populations shown below. 


Unlock Deck
Unlock for access to all 112 flashcards in this deck.
Unlock Deck
k this deck
14
Use the Hill-Huntington method of apportionment to distribute 12 seats on a city council to three districts with the populations shown below. 


Unlock Deck
Unlock for access to all 112 flashcards in this deck.
Unlock Deck
k this deck
15
Use the Hamilton method of apportionment to distribute 15 representatives to the three states with the populations shown below. 


Unlock Deck
Unlock for access to all 112 flashcards in this deck.
Unlock Deck
k this deck
16
Use the Hill-Huntington method of apportionment to distribute 15 representatives to the three states with the populations shown below. 


Unlock Deck
Unlock for access to all 112 flashcards in this deck.
Unlock Deck
k this deck
17
Use the Webster method of apportionment to distribute 15 representatives to the three states with the populations shown below. 


Unlock Deck
Unlock for access to all 112 flashcards in this deck.
Unlock Deck
k this deck
18
Use the Hamilton method of apportionment to distribute representatives.

Unlock Deck
Unlock for access to all 112 flashcards in this deck.
Unlock Deck
k this deck
19
Given the cities and the populations below, use the Hill-Huntington method of apportionment to distribute 25 seats on a regional board. 


Unlock Deck
Unlock for access to all 112 flashcards in this deck.
Unlock Deck
k this deck
20
The Hamilton method of apportionment always satisfies what is called the "quota condition." What does this mean?

Unlock Deck
Unlock for access to all 112 flashcards in this deck.
Unlock Deck
k this deck
21
Use the Hamilton's method to determine how many cars should go to each precinct.

Unlock Deck
Unlock for access to all 112 flashcards in this deck.
Unlock Deck
k this deck
22
A town board has 10 members, divided among three regions of the town using the Hamilton method of apportionment. The regions and their populations are shown below. Find the difference in district population for the North and South regions. 


Unlock Deck
Unlock for access to all 112 flashcards in this deck.
Unlock Deck
k this deck
23
A country has three states with the populations shown below. The House of Representatives for the country is to have 15 members. Find the district population for each state if the country uses the Jefferson method of apportionment. 


Unlock Deck
Unlock for access to all 112 flashcards in this deck.
Unlock Deck
k this deck
24
The manager of a busy restaurant is working on a schedule for the restaurant's 25 food servers. There are three shifts, as identified below: 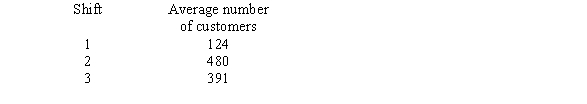 Use the Hill-Huntington method to determine how many food servers should be scheduled for each shift.
Use the Hill-Huntington method to determine how many food servers should be scheduled for each shift.
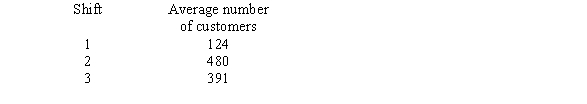 Use the Hill-Huntington method to determine how many food servers should be scheduled for each shift.
Use the Hill-Huntington method to determine how many food servers should be scheduled for each shift.
Unlock Deck
Unlock for access to all 112 flashcards in this deck.
Unlock Deck
k this deck
25
A town board has 10 members, divided among three regions of the town using the Hamilton method of apportionment. The regions and their populations are given below. Find the difference in representative share for the North and South regions. 


Unlock Deck
Unlock for access to all 112 flashcards in this deck.
Unlock Deck
k this deck
26
The manager of a busy restaurant is working on a schedule for the restaurant's 25 food servers. There are three shifts, as identified below: 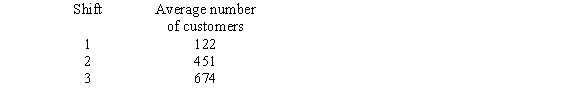 Use the Hamilton method to determine how many food servers should be scheduled for each shift.
Use the Hamilton method to determine how many food servers should be scheduled for each shift.
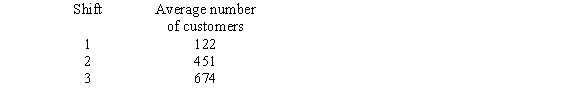 Use the Hamilton method to determine how many food servers should be scheduled for each shift.
Use the Hamilton method to determine how many food servers should be scheduled for each shift.
Unlock Deck
Unlock for access to all 112 flashcards in this deck.
Unlock Deck
k this deck
27
A small country has four states and a House of Representatives with 20 seats. Given the states, populations, and apportionment below, find the percentage difference in district population between states A and C. 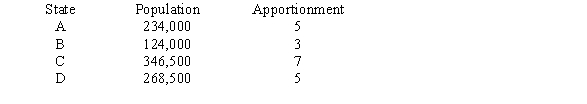
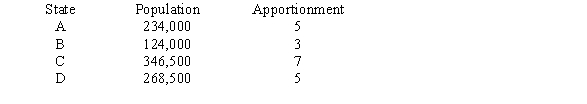

Unlock Deck
Unlock for access to all 112 flashcards in this deck.
Unlock Deck
k this deck
28
What is the geometric mean of 7 and 8? Use four decimal places.

Unlock Deck
Unlock for access to all 112 flashcards in this deck.
Unlock Deck
k this deck
29
List three paradoxes of the Hamilton method.

Unlock Deck
Unlock for access to all 112 flashcards in this deck.
Unlock Deck
k this deck
30
What is the Hill-Huntington rounding point of 6.475? Use four decimal places.

Unlock Deck
Unlock for access to all 112 flashcards in this deck.
Unlock Deck
k this deck
31
Among all divisor methods, which method shows no bias with regard to state population?

Unlock Deck
Unlock for access to all 112 flashcards in this deck.
Unlock Deck
k this deck
32
The manager of a busy restaurant is working on a schedule for the restaurant's 25 food servers. There are three shifts, as identified below:  Use the Jefferson method to determine how many food servers should be scheduled for each shift.
Use the Jefferson method to determine how many food servers should be scheduled for each shift.
 Use the Jefferson method to determine how many food servers should be scheduled for each shift.
Use the Jefferson method to determine how many food servers should be scheduled for each shift.
Unlock Deck
Unlock for access to all 112 flashcards in this deck.
Unlock Deck
k this deck
33
Use the Jefferson's method to determine how many cars should go to each precinct.

Unlock Deck
Unlock for access to all 112 flashcards in this deck.
Unlock Deck
k this deck
34
The manager of a busy restaurant is working on a schedule for the restaurant's 25 food servers. There are three shifts, as identified below: 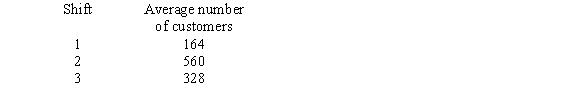 Use the Webster method to determine how many food servers should be scheduled for each shift.
Use the Webster method to determine how many food servers should be scheduled for each shift.
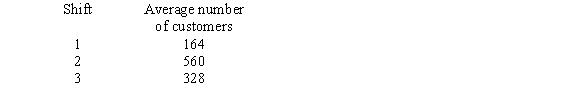 Use the Webster method to determine how many food servers should be scheduled for each shift.
Use the Webster method to determine how many food servers should be scheduled for each shift.
Unlock Deck
Unlock for access to all 112 flashcards in this deck.
Unlock Deck
k this deck
35
Use the Hill-Huntington method to determine how many cars should go to each precinct.

Unlock Deck
Unlock for access to all 112 flashcards in this deck.
Unlock Deck
k this deck
36
A city is divided into four regions for distributing the 20 representatives on a public utility board. The regions and their populations are shown below. The board uses the Hamilton method of apportionment to distribute seats. Find the representative share for each region based on this apportionment. 


Unlock Deck
Unlock for access to all 112 flashcards in this deck.
Unlock Deck
k this deck
37
Use the following information to answer Questions 32-35.
Thirty patrol cars are to be apportioned to three precincts according to the monthly crime totals, which are as follows:
Precinct Crimes reported last month
I 94
II 130
III 108
Use the Webster's method to determine how many cars should go to each precinct.
Thirty patrol cars are to be apportioned to three precincts according to the monthly crime totals, which are as follows:
Precinct Crimes reported last month
I 94
II 130
III 108
Use the Webster's method to determine how many cars should go to each precinct.

Unlock Deck
Unlock for access to all 112 flashcards in this deck.
Unlock Deck
k this deck
38
A small country has four states and a House of Representatives with 20 seats. Given the states, populations, and apportionment below, find the percentage difference in representative share between states A and C. 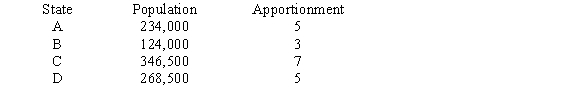
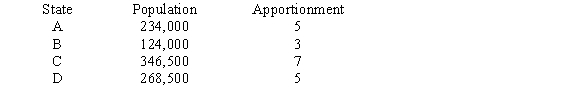

Unlock Deck
Unlock for access to all 112 flashcards in this deck.
Unlock Deck
k this deck
39
What is the Hill-Huntington rounding of 6.475?

Unlock Deck
Unlock for access to all 112 flashcards in this deck.
Unlock Deck
k this deck
40
A country has three states with the populations shown below. The House of Representatives for the country is to have 15 members. Find the representative share for each state if the country uses the Jefferson method of apportionment. 


Unlock Deck
Unlock for access to all 112 flashcards in this deck.
Unlock Deck
k this deck
41
The d'Hondt method always leads to the same apportionment as Jefferson's method.

Unlock Deck
Unlock for access to all 112 flashcards in this deck.
Unlock Deck
k this deck
42
The Jefferson method of apportionment can display the population paradox.

Unlock Deck
Unlock for access to all 112 flashcards in this deck.
Unlock Deck
k this deck
43
For a given set of populations and house sizes, different methods of apportionment may lead to different apportionments.

Unlock Deck
Unlock for access to all 112 flashcards in this deck.
Unlock Deck
k this deck
44
The Hamilton method of apportionment can display the population paradox.

Unlock Deck
Unlock for access to all 112 flashcards in this deck.
Unlock Deck
k this deck
45
Use the following information to answer the Questions:
Three states have the following populations: A house of representatives with 17 members is to be apportioned among these states.
-What is the tentative apportionment for state A using Hamilton's method?
A) 8
B) 8.5
C) 9
D) 9.5
Three states have the following populations: A house of representatives with 17 members is to be apportioned among these states.
-What is the tentative apportionment for state A using Hamilton's method?
A) 8
B) 8.5
C) 9
D) 9.5

Unlock Deck
Unlock for access to all 112 flashcards in this deck.
Unlock Deck
k this deck
46
An apportionment method exists that satisfies the quota condition and is free from both the population paradox and the Alabama paradox.

Unlock Deck
Unlock for access to all 112 flashcards in this deck.
Unlock Deck
k this deck
47
We are scheduling seven course sections for a total of 217 students. Enrollments are 109 in calculus I, 79 in calculus II, 29 in advanced calculus. Find the apportionment for advanced calculus using the Hamilton method.
A) 0
B) 1
C) 2
D) 3
A) 0
B) 1
C) 2
D) 3

Unlock Deck
Unlock for access to all 112 flashcards in this deck.
Unlock Deck
k this deck
48
The Jefferson method of apportionment can display the Alabama paradox.

Unlock Deck
Unlock for access to all 112 flashcards in this deck.
Unlock Deck
k this deck
49
Use the following information to answer the Questions:
Three states have the following populations: A house of representatives with 17 members is to be apportioned among these states.
-What is the tentative apportionment for state C using Webster's method?
A) 0
B) 1
C) 2
D) 3
Three states have the following populations: A house of representatives with 17 members is to be apportioned among these states.
-What is the tentative apportionment for state C using Webster's method?
A) 0
B) 1
C) 2
D) 3

Unlock Deck
Unlock for access to all 112 flashcards in this deck.
Unlock Deck
k this deck
50
For a given set of populations and house sizes, different methods of apportionment may lead to the same apportionment.

Unlock Deck
Unlock for access to all 112 flashcards in this deck.
Unlock Deck
k this deck
51
The Webster method of apportionment can display the population paradox.

Unlock Deck
Unlock for access to all 112 flashcards in this deck.
Unlock Deck
k this deck
52
A county is divided into three districts with the populations shown below. There are 10 seats on the county council that need to be apportioned, using the Hamilton method. Find the apportionment for the Applewood district. 
A) 4
B) 3
C) 5
D) 2

A) 4
B) 3
C) 5
D) 2

Unlock Deck
Unlock for access to all 112 flashcards in this deck.
Unlock Deck
k this deck
53
We are scheduling seven course sections for a total of 217 students. Enrollments are 109 in calculus I, 79 in calculus II, and 29 in advanced calculus. Find the quota of sections for calculus II.
A) 2
B) 2.55
C) 3.64
D) 3
A) 2
B) 2.55
C) 3.64
D) 3

Unlock Deck
Unlock for access to all 112 flashcards in this deck.
Unlock Deck
k this deck
54
Which of the following is a true statement?
A) Jefferson's method of apportionment is not biased with respect to a state's population.
B) Jefferson's method of apportionment is biased toward states with smaller populations.
C) Jefferson's method of apportionment is biased toward states with larger populations.
A) Jefferson's method of apportionment is not biased with respect to a state's population.
B) Jefferson's method of apportionment is biased toward states with smaller populations.
C) Jefferson's method of apportionment is biased toward states with larger populations.

Unlock Deck
Unlock for access to all 112 flashcards in this deck.
Unlock Deck
k this deck
55
A county is divided into three districts with the populations shown below. There are 10 seats on the county council that need to be apportioned. Find the quota for the Applewood district. 
A) 4.57
B) 4
C) 5
D) 8.28

A) 4.57
B) 4
C) 5
D) 8.28

Unlock Deck
Unlock for access to all 112 flashcards in this deck.
Unlock Deck
k this deck
56
Use the following information to answer the Questions:
Three states have the following populations: A house of representatives with 17 members is to be apportioned among these states.
-What is the tentative apportionment for state A using the Hill-Huntington method?
A) 8
B) 8.5
C) 9
D) 9.5
Three states have the following populations: A house of representatives with 17 members is to be apportioned among these states.
-What is the tentative apportionment for state A using the Hill-Huntington method?
A) 8
B) 8.5
C) 9
D) 9.5

Unlock Deck
Unlock for access to all 112 flashcards in this deck.
Unlock Deck
k this deck
57
Use the following information to answer the Questions:
Three states have the following populations: A house of representatives with 17 members is to be apportioned among these states.
-What is the standard divisor?
A) 1100.50
B) 1180.50
C) 1181.76
D) 1200
Three states have the following populations: A house of representatives with 17 members is to be apportioned among these states.
-What is the standard divisor?
A) 1100.50
B) 1180.50
C) 1181.76
D) 1200

Unlock Deck
Unlock for access to all 112 flashcards in this deck.
Unlock Deck
k this deck
58
Which method of apportionment always satisfies the quota condition?
A) Hamilton
B) Hill-Huntington
C) Jefferson
D) Webster
A) Hamilton
B) Hill-Huntington
C) Jefferson
D) Webster

Unlock Deck
Unlock for access to all 112 flashcards in this deck.
Unlock Deck
k this deck
59
A small county has populations in three districts as shown below. They are to apportion 10 seats on the county council. Find the quota for Riverdale. 
A) 4.13
B) 2
C) 4
D) 2.42

A) 4.13
B) 2
C) 4
D) 2.42

Unlock Deck
Unlock for access to all 112 flashcards in this deck.
Unlock Deck
k this deck
60
Use the following information to answer the Questions:
Three states have the following populations: A house of representatives with 17 members is to be apportioned among these states.
-What is the quota for state B?
A) 6
B) 6.8
C) 7
D) 7.4
Three states have the following populations: A house of representatives with 17 members is to be apportioned among these states.
-What is the quota for state B?
A) 6
B) 6.8
C) 7
D) 7.4

Unlock Deck
Unlock for access to all 112 flashcards in this deck.
Unlock Deck
k this deck
61
A county is divided into three districts with the populations shown below. There are 10 seats on the county council that need to be apportioned. If the county uses the d'Hondt method, what is the initial priority number for Central? 
A) 476
B) 522
C) 5220
D) 5221

A) 476
B) 522
C) 5220
D) 5221

Unlock Deck
Unlock for access to all 112 flashcards in this deck.
Unlock Deck
k this deck
62
A county is divided into three districts with the populations shown below. There are 10 seats on the county council that need to be apportioned. What would be the standard divisor? 
A) 1533
B) 1656
C) 1740
D) 1810

A) 1533
B) 1656
C) 1740
D) 1810

Unlock Deck
Unlock for access to all 112 flashcards in this deck.
Unlock Deck
k this deck
63
A state has four districts with the populations shown below. The House of Representatives has 20 seats that are to be apportioned using the d'Hondt method. After District B has received 3 seats, what is its new priority number? 
A) 14,000
B) 28,000
C) 56,000
D) None of the above.

A) 14,000
B) 28,000
C) 56,000
D) None of the above.

Unlock Deck
Unlock for access to all 112 flashcards in this deck.
Unlock Deck
k this deck
64
A county has three districts with the populations shown below. The 11 seats on the county council are to be apportioned using the d'Hondt method. After District A receives its second seat, what is its priority number? 
A) 14,000
B) 14,333.3
C) 15,300
D) None of the above.

A) 14,000
B) 14,333.3
C) 15,300
D) None of the above.

Unlock Deck
Unlock for access to all 112 flashcards in this deck.
Unlock Deck
k this deck
65
A county has three districts with the populations shown below. The 11 seats on the county council are to be apportioned using the Webster method. Find the apportionment for each district. 
A) 5, 4, 2
B) 5, 3, 3
C) 4, 4, 3
D) 6, 3, 2

A) 5, 4, 2
B) 5, 3, 3
C) 4, 4, 3
D) 6, 3, 2

Unlock Deck
Unlock for access to all 112 flashcards in this deck.
Unlock Deck
k this deck
66
Find the geometric mean of 5 and 6.
A) 5.5
B) 5.48
C) 4.69
D) 3.32
A) 5.5
B) 5.48
C) 4.69
D) 3.32

Unlock Deck
Unlock for access to all 112 flashcards in this deck.
Unlock Deck
k this deck
67
A small county has populations in three districts as shown below. They are to apportion 15 seats on the county council using the Webster method. Find the apportionment for each district. 
A) 7, 5, 3
B) 6, 6, 3
C) 6, 5, 4
D) 7, 4, 4

A) 7, 5, 3
B) 6, 6, 3
C) 6, 5, 4
D) 7, 4, 4

Unlock Deck
Unlock for access to all 112 flashcards in this deck.
Unlock Deck
k this deck
68
Find the geometric mean of 3 and 7.
A) 4.38
B) 5.00
C) 4.58
D) 3.16
A) 4.38
B) 5.00
C) 4.58
D) 3.16

Unlock Deck
Unlock for access to all 112 flashcards in this deck.
Unlock Deck
k this deck
69
A state has four districts with the populations shown below. The House of Representatives has 20 seats that are to be apportioned using the Jefferson method. Find the apportionment for each district. 
A) 6, 5, 6, 3
B) 7, 4, 5, 4
C) 6, 4, 6, 4
D) 7, 4, 6, 3

A) 6, 5, 6, 3
B) 7, 4, 5, 4
C) 6, 4, 6, 4
D) 7, 4, 6, 3

Unlock Deck
Unlock for access to all 112 flashcards in this deck.
Unlock Deck
k this deck
70
A country has four states with the populations shown below. The House of Representatives is to have 15 members. Use the Hill-Huntington method of apportionment to find the number of seats for each state. 
A) 5, 4, 4, 2
B) 6, 4, 3, 2
C) 5, 4, 3, 3
D) 6, 3, 3, 3

A) 5, 4, 4, 2
B) 6, 4, 3, 2
C) 5, 4, 3, 3
D) 6, 3, 3, 3

Unlock Deck
Unlock for access to all 112 flashcards in this deck.
Unlock Deck
k this deck
71
Use the following information to answer the Questions:
A senate of 20 faculty members represents three departments: math, statistics, and applied math. The seats are to be apportioned according to the numbers of students in each department, which are as follows:
-What apportionment is produced by Jefferson's method?
A) 5, 5, 10
B) 6, 5, 9
C) 7, 4, 9
D) 6, 4, 10
A senate of 20 faculty members represents three departments: math, statistics, and applied math. The seats are to be apportioned according to the numbers of students in each department, which are as follows:
-What apportionment is produced by Jefferson's method?
A) 5, 5, 10
B) 6, 5, 9
C) 7, 4, 9
D) 6, 4, 10

Unlock Deck
Unlock for access to all 112 flashcards in this deck.
Unlock Deck
k this deck
72
A country has four states with the populations shown below. The House of Representatives is to have 15 members. Use the Webster method of apportionment to find the number of seats for each state. 
A) 6, 4, 3, 2
B) 5, 4, 4, 2
C) 6, 3, 3, 3
D) 5, 4, 3, 3

A) 6, 4, 3, 2
B) 5, 4, 4, 2
C) 6, 3, 3, 3
D) 5, 4, 3, 3

Unlock Deck
Unlock for access to all 112 flashcards in this deck.
Unlock Deck
k this deck
73
A country has four states with the populations shown below. The House of Representatives is to have 15 members, apportioned by the Hill-Huntington method. Find the tentative apportionment for district C. 
A) 3
B) 3.4
C) 3.46
D) 4

A) 3
B) 3.4
C) 3.46
D) 4

Unlock Deck
Unlock for access to all 112 flashcards in this deck.
Unlock Deck
k this deck
74
A county has three districts with the populations shown below. The 11 seats on the county council are to be apportioned using the Jefferson method. Find the apportionment for each district. 
A) 5, 3, 3
B) 5, 4, 2
C) 6, 3, 2
D) 4, 4, 3

A) 5, 3, 3
B) 5, 4, 2
C) 6, 3, 2
D) 4, 4, 3

Unlock Deck
Unlock for access to all 112 flashcards in this deck.
Unlock Deck
k this deck
75
A county is divided into three districts with the populations shown below. There are 10 seats on the county council that need to be apportioned, using the Hamilton method. Find the apportionment for the Boxwood district. 
A) 2
B) 3
C) 1
D) 4

A) 2
B) 3
C) 1
D) 4

Unlock Deck
Unlock for access to all 112 flashcards in this deck.
Unlock Deck
k this deck
76
A county has four districts with the populations shown below. They are to use the Hill -Huntington method of apportionment to distribute 20 seats on a county council. Find the tentative apportionment for district B. 
A) 3
B) 4
C) 5
D) 6

A) 3
B) 4
C) 5
D) 6

Unlock Deck
Unlock for access to all 112 flashcards in this deck.
Unlock Deck
k this deck
77
A county has three districts with the populations shown below. The 11 seats on the county council are to be apportioned using the Webster method. Find the tentative apportionment for district A. 
A) 4
B) 4.5
C) 4.73
D) 5

A) 4
B) 4.5
C) 4.73
D) 5

Unlock Deck
Unlock for access to all 112 flashcards in this deck.
Unlock Deck
k this deck
78
Find the geometric mean of 8 and 9.
A) 5.83
B) 8.5
C) 8.74
D) 8.49
A) 5.83
B) 8.5
C) 8.74
D) 8.49

Unlock Deck
Unlock for access to all 112 flashcards in this deck.
Unlock Deck
k this deck
79
Given three states with the populations shown below, and a national senate with 10 seats, use the Hill-Huntington method of apportionment to distribute the seats to the states. 
A) 4, 3, 3
B) 4, 4, 2
C) 5, 4, 1
D) 5, 3, 2

A) 4, 3, 3
B) 4, 4, 2
C) 5, 4, 1
D) 5, 3, 2

Unlock Deck
Unlock for access to all 112 flashcards in this deck.
Unlock Deck
k this deck
80
A small county has populations in three districts as shown below. They are to apportion 15 seats on the county council using the Hill-Huntington method. Find the apportionment for each district. 
A) 7, 5, 3
B) 6, 6, 3
C) 6, 5, 4
D) 7, 4, 4

A) 7, 5, 3
B) 6, 6, 3
C) 6, 5, 4
D) 7, 4, 4

Unlock Deck
Unlock for access to all 112 flashcards in this deck.
Unlock Deck
k this deck


