Deck 10: Rotation
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/85
Play
Full screen (f)
Deck 10: Rotation
1
If the angular velocity vector of a spinning body points out of the page then, when viewed from above the page, the body is spinning:
A) clockwise about an axis that is perpendicular to the page
B) counterclockwise about an axis that is perpendicular to the page
C) about an axis that is parallel to the page
D) about an axis that is changing orientation
E) about an axis that is getting longer
A) clockwise about an axis that is perpendicular to the page
B) counterclockwise about an axis that is perpendicular to the page
C) about an axis that is parallel to the page
D) about an axis that is changing orientation
E) about an axis that is getting longer
counterclockwise about an axis that is perpendicular to the page
2
If a wheel turning at a constant rate completes 100 revolutions in 10 s its angular speed is:
A) 0.31 rad/s
B) 0.63 rad/s
C) 10 rad/s
D) 31 rad/s
E) 63 rad/s
A) 0.31 rad/s
B) 0.63 rad/s
C) 10 rad/s
D) 31 rad/s
E) 63 rad/s
63 rad/s
3
A wheel initially has an angular velocity of 36 rad/s but after 6.0s its angular velocity is 24 rad/s. If its angular acceleration is constant the value is:
A) 2.0 rad/s2
B) -2.0 rad/s2
C) 3.0 rad/s2
D) -3.0 rad/s2
E) 6.0 rad/s2
A) 2.0 rad/s2
B) -2.0 rad/s2
C) 3.0 rad/s2
D) -3.0 rad/s2
E) 6.0 rad/s2
-2.0 rad/s2
4
A flywheel is initially roatating at 20 rad/s and has a constant angular acceleration. After 9.0 s it has rotated through 450 rad. Its angular acceleration is:
A) 3.3 rad/s
B) 4.4 rad/s
C) 5.6 rad/s
D) 6.7 rad/s
E) 11 rad/s
A) 3.3 rad/s
B) 4.4 rad/s
C) 5.6 rad/s
D) 6.7 rad/s
E) 11 rad/s

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
5
A wheel initially has an angular velocity of 18 rad/s but it is slowing at a rate of 2.0 rad/s2. By the time it stops it will have turned through:
A) 81 rad
B) 160 rad
C) 245 rad
D) 330 rad
E) 410 rad
A) 81 rad
B) 160 rad
C) 245 rad
D) 330 rad
E) 410 rad

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
6
A wheel starts from rest and has an angular acceleration of 4.0 rad/s2. When it has made 10 rev its angular velocity is:
A) 16 rad/s
B) 22 rad/s
C) 32 rad/s
D) 250 rad/s
E) 500 rad/s
A) 16 rad/s
B) 22 rad/s
C) 32 rad/s
D) 250 rad/s
E) 500 rad/s

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
7
A phonograph turntable, initially rotating at 0.75 rev/s, slows down and stops in 30 s. The magnitude of its average angular acceleration in rad/s2 for this process is:
A) 1.5
B) 1.5
C) /40
D) /20
E) 0.75
A) 1.5
B) 1.5
C) /40
D) /20
E) 0.75

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
8
The angular velocity of a rotating wheel increases 2 rev/s every minute. The angular acceleration, in rad/s2 of this wheel is:
A) 4 2
B) 2
C) 1/30
D) 2 /30
E) 4
A) 4 2
B) 2
C) 1/30
D) 2 /30
E) 4

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
9
If a wheel is turning at 3.0 rad/s, the time it takes to complete one revolution is about:
A) 0.33 s
B) 0.67 s
C) 1.0 s
D) 1.3 s
E) 2.1 s
A) 0.33 s
B) 0.67 s
C) 1.0 s
D) 1.3 s
E) 2.1 s

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
10
The angular speed of the second hand of a watch is:
A) ( /1800) rad/s
B) ( /60) m/s
C) ( /30) m/s
D) (2 ) m/s
E) (60) m/s
A) ( /1800) rad/s
B) ( /60) m/s
C) ( /30) m/s
D) (2 ) m/s
E) (60) m/s

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
11
A flywheel rotating at 12 rev/s is brought to rest in 6 s. The magnitude of the average angular acceleration in rad/s2 of the wheel during this process is:
A) 1/
B) 2
C) 4
D) 4
E) 72
A) 1/
B) 2
C) 4
D) 4
E) 72

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
12
A wheel rotates with a constant angular acceleration of rad/s2. During a certain time interval its angular displacement is rad. At the end of the interval its angular velocity is 2 rad/s. Its angular velocity at the beginning of the interval is:
A) zero
B) 1 ras/s
C) ras/s
D)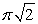 ras/s
ras/s
E) 2 ras/s
A) zero
B) 1 ras/s
C) ras/s
D)
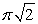 ras/s
ras/sE) 2 ras/s

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
13
One revolution per minute is about:
A) 0.0524 rad/s
B) 0.105 rad/s
C) 0.95 rad/s
D) 1.57 rad/s
E) 6.28 rad/s
A) 0.0524 rad/s
B) 0.105 rad/s
C) 0.95 rad/s
D) 1.57 rad/s
E) 6.28 rad/s

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
14
A wheel initially has an angular velocity of 18 rad/s. It has a constant angular acceleration of 2.0 rad/s2 and is slowing at first. What time elapses before its angular velocity is18 rad/s in the direction opposite to its initial angular velocity?
A) 3.0 s
B) 6.0 s
C) 9.0 s
D) 18 s
E) 36 s
A) 3.0 s
B) 6.0 s
C) 9.0 s
D) 18 s
E) 36 s

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
15
The angular speed of the minute hand of a watch is:
A) (60/ ) m/s
B) (1800/ ) m/s
C) ( ) m/s
D) ( /1800) m/s
E) ( /60) m/s
A) (60/ ) m/s
B) (1800/ ) m/s
C) ( ) m/s
D) ( /1800) m/s
E) ( /60) m/s

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
16
Ten seconds after an electric fan is turned on, the fan rotates at 300 rev/min. Its average angular acceleration is:
A) 3.14 rad/s2
B) 30 rad/s2
C) 30 rev/s2
D) 50 rev/min2
E) 1800 rev/s2
A) 3.14 rad/s2
B) 30 rad/s2
C) 30 rev/s2
D) 50 rev/min2
E) 1800 rev/s2

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
17
A wheel initially has an angular velocity of -36 rad/s but after 6.0 s its angular velocity is -24 rad/s. If its angular acceleration is constant the value is:
A) 2.0 rad/s2
B) -2.0 rad/s2
C) 3.0 rad/s2
D) -3.0 rad/s2
E) -6.0 rad/s2
A) 2.0 rad/s2
B) -2.0 rad/s2
C) 3.0 rad/s2
D) -3.0 rad/s2
E) -6.0 rad/s2

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
18
The angular velocity vector of a spinning body points out of the page. If the angular acceleration vector points into the page then:
A) the body is slowing down
B) the body is speeding up
C) the body is starting to turn in the opposite direction
D) the axis of rotation is changing orientation
E) none of the above
A) the body is slowing down
B) the body is speeding up
C) the body is starting to turn in the opposite direction
D) the axis of rotation is changing orientation
E) none of the above

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
19
A radian is about:
A) 25
B) 37
C) 45
D) 57
E) 90
A) 25
B) 37
C) 45
D) 57
E) 90

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
20
One revolution is the same as:
A) 1 rad
B) 57 rad
C) /2 rad
D) rad
E) 2 rad
A) 1 rad
B) 57 rad
C) /2 rad
D) rad
E) 2 rad

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
21
A wheel starts from rest and has an angular acceleration that is given by (t) = (6.0 rad/s4)t2. After it has turned through 10 rev its angular velocity is:
A) 63 rad/s
B) 75 rad/s
C) 89 rad/s
D) 130 rad/s
E) 210 rad/s
A) 63 rad/s
B) 75 rad/s
C) 89 rad/s
D) 130 rad/s
E) 210 rad/s

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
22
A car travels north at constant velocity. It goes over a piece of mud which sticks to the tire. The initial acceleration of the mud, as it leaves the ground, is:
A) vertically upward
B) horizontally to the north
C) horizontally to the south
D) zero
E) upward and forward at 45 to the horizontal
A) vertically upward
B) horizontally to the north
C) horizontally to the south
D) zero
E) upward and forward at 45 to the horizontal

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
23
A wheel starts from rest and has an angular acceleration that is given by (t) = 6rad/s4)t2. The angle through which it turns in time t is given by:
A) [(1/8)t4] rad
B) [(1/4)t4] rad
C) [(1/2)t4] rad
D) (t4) rad
E) 12 rad
A) [(1/8)t4] rad
B) [(1/4)t4] rad
C) [(1/2)t4] rad
D) (t4) rad
E) 12 rad

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
24
If a wheel turns with constant angular speed then:
A) each point on its rim moves with constant velocity
B) each point on its rim moves with constant acceleration
C) the wheel turns through equal angles in equal times
D) the angle through which the wheel turns in each second increases as time goes on
E) the angle through which the wheel turns in each second decreases as time goes on
A) each point on its rim moves with constant velocity
B) each point on its rim moves with constant acceleration
C) the wheel turns through equal angles in equal times
D) the angle through which the wheel turns in each second increases as time goes on
E) the angle through which the wheel turns in each second decreases as time goes on

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
25
A wheel starts from rest and has an angular acceleration of 4.0 rad/s2. The time it takes to make 10 revolutions is:
A) 0.50 s
B) 0.71 s
C) 2.2 s
D) 2.8 s
E) 5.6 s
A) 0.50 s
B) 0.71 s
C) 2.2 s
D) 2.8 s
E) 5.6 s

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
26
Wrapping paper is being from a 5.0-cm radius tube, free to rotate on its axis. If it is pulled at the constant rate of 10 cm/s and does not slip on the tube, the angular velocity of the tube is:
A) 2.0 rad/s
B) 5.0 rad/s
C) 10 rad/s
D) 25 rad/s
E) 50 rad/s
A) 2.0 rad/s
B) 5.0 rad/s
C) 10 rad/s
D) 25 rad/s
E) 50 rad/s

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
27
A flywheel of diameter 1.2 m has a constant angular acceleration of 5.0 rad/s2. The tangential acceleration of a point on its rim is:
A) 5.0 rad/s2
B) 3.0 m/s2
C) 5.0 m/s2
D) 6.0 m/s2
E) 12 m/s2
A) 5.0 rad/s2
B) 3.0 m/s2
C) 5.0 m/s2
D) 6.0 m/s2
E) 12 m/s2

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
28
The magnitude of the acceleration of a point on a spinning wheel is increased by a factor of 4 if:
A) the magnitues of the angular velocity and the angular acceleration are each multiplied by a factor of 4
B) the magnitues of the angular velocity is multuplied by a factor of 4 and the angular acceleration is not changed
C) the magnitues of the angular velocity and the angular acceleration are each multiplied by a factor of 2
D) the magnitues of the angular velocity is multiplied by a factor of 2 and the angular acceleration is not changed
E) the magnitues of the angular velocity is multiplied by a factor of 2 and the magnitudeof the angular acceleration is multiplied by a factor of 4
A) the magnitues of the angular velocity and the angular acceleration are each multiplied by a factor of 4
B) the magnitues of the angular velocity is multuplied by a factor of 4 and the angular acceleration is not changed
C) the magnitues of the angular velocity and the angular acceleration are each multiplied by a factor of 2
D) the magnitues of the angular velocity is multiplied by a factor of 2 and the angular acceleration is not changed
E) the magnitues of the angular velocity is multiplied by a factor of 2 and the magnitudeof the angular acceleration is multiplied by a factor of 4

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
29
A particle moves in a circular path of radius 0.10 m with a constant angular speed of 5 rev/s. The acceleration of the particle is:
A) 0.10 m/s2
B) 0.50 m/s2
C) 500 m/s2
D) 1000 2 m/s2
E) 10 2 m/s2
A) 0.10 m/s2
B) 0.50 m/s2
C) 500 m/s2
D) 1000 2 m/s2
E) 10 2 m/s2

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
30
The figure shows a cylinder of radius 0.7 m rotating about its axis at 10 rad/s. The speed of the point P is: 
A) 7.0 m/s
B) 14 rad/s
C) 7 rad/s
D) 0.70 m/s
E) none of these

A) 7.0 m/s
B) 14 rad/s
C) 7 rad/s
D) 0.70 m/s
E) none of these

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
31
A wheel starts from rest and has an angular acceleration that is given by (t) = (6.0 rad/s4)t2. The time it takes to make 10 rev is:
A) 2.8 s
B) 3.3 s
C) 4.0 s
D) 4.7 s
E) 5.3 s
A) 2.8 s
B) 3.3 s
C) 4.0 s
D) 4.7 s
E) 5.3 s

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
32
A child, riding on a large merry-go-round, travels a distance of 3000 m in a circle of diameter 40 m. The total angle through which she revolves is:
A) 50 rad
B) 75 rad
C) 150 rad
D) 314 rad
E) none of these
A) 50 rad
B) 75 rad
C) 150 rad
D) 314 rad
E) none of these

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
33
A wheel is spinning at 27 rad/s but is slowing with an angular acceleration that has a magnitude given by (3.0 rad/s4)t2. It stops in a time of:
A) 1.7 s
B) 2.6 s
C) 3.0 s
D) 4.4 s
E) 7.3 s
A) 1.7 s
B) 2.6 s
C) 3.0 s
D) 4.4 s
E) 7.3 s

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
34
For a wheel spinning on an axis through its center, the ratio of the radial acceleration of a point on the rim to the radial acceleration of a point halfway between the center and the rim is:
A) 1
B) 2
C) 1/2
D) 4
E) 1/4
A) 1
B) 2
C) 1/2
D) 4
E) 1/4

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
35
For a wheel spinning on an axis through its center, the ratio of the tangential acceleration of a point on the rim to the tangential acceleration of a point halfway between the center and the rim is:
A) 1
B) 2
C) 1/2
D) 4
E) 1/4
A) 1
B) 2
C) 1/2
D) 4
E) 1/4

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
36
String is wrapped around the periphery of a 5.0-cm radius cylinder, free to rotate on its axis. The string is pulled straight out at a constant rate of 10 cm/s and does not slip on the cylinder. As each small segment of string leaves the cylinder, its acceleration changes by:
A) 0
B) 0.010 m/s2
C) 0.020 m/s2
D) 0.10 m/s2
E) 0.20 m/s2
A) 0
B) 0.010 m/s2
C) 0.020 m/s2
D) 0.10 m/s2
E) 0.20 m/s2

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
37
For a wheel spinning with constant angular acceleration on an axis through its center, the ratio of the speed of a point on the rim to the speed of a point halfway between the center and the rim is:
A) 1
B) 2
C) 1/2
D) 4
E) 1/4
A) 1
B) 2
C) 1/2
D) 4
E) 1/4

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
38
Two wheels are identical but wheel B is spinning with twice the angular speed of wheel A. The ratio of the magnitued of the radical acceleration of a point on the rim of B to the magnitude of the radial acceleration of a point on the rim of A is:
A) 1
B) 2
C) 1/2
D) 4
E) 1/4
A) 1
B) 2
C) 1/2
D) 4
E) 1/4

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
39
A wheel of diameter 3.0 cm has a 4.0 m cord wrapped around its periphery. Starting from rest, the wheel is given a constant angular acceleration of 2 rad/s2. The cord will unwind in:
A) 0.82 s
B) 2.0 s
C) 8.0 s
D) 16 s
E) 130 s
A) 0.82 s
B) 2.0 s
C) 8.0 s
D) 16 s
E) 130 s

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
40
The fan shown has been turned on and is slowing as it rotates clockwise. The direction of the acceleration of the acceleratrion point X on the fan tip could be: 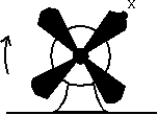
A)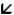
B)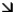
C)
D)
E)

A)
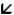
B)
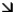
C)
D)
E)

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
41
A and B are two solid cylinders made of aluminum. Their dimensions are shown. The ratio of the rotational inertia of B to that of A about the common axis X─X' is: 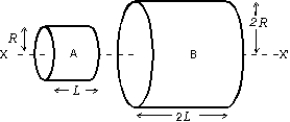
A) 2
B) 4
C) 8
D) 16
E) 32

A) 2
B) 4
C) 8
D) 16
E) 32

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
42
A force with a given magnitude is to be applied to a wheel. The torque can be maximized by:
A) applying the force near the axle, radially outward from the axle
B) applying the force near the rim, radially outward from the axle
C) applying the force near the axle, parallel to a tangent to the wheel
D) applying the force at the rim, tangent to the rim
E) applying the force at the rim, at 45 to the tangent
A) applying the force near the axle, radially outward from the axle
B) applying the force near the rim, radially outward from the axle
C) applying the force near the axle, parallel to a tangent to the wheel
D) applying the force at the rim, tangent to the rim
E) applying the force at the rim, at 45 to the tangent

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
43
Two uniform circular disks having the same mass and the same thickness are made from different materials. The disk with the smaller rotational inertia is:
A) the one made from the more dense material
B) the one made from the less dense material
C) neither - both rotational inertias are the same
D) the disk with the larger angular velocity
E) the disk with the larger torque
A) the one made from the more dense material
B) the one made from the less dense material
C) neither - both rotational inertias are the same
D) the disk with the larger angular velocity
E) the disk with the larger torque

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
44
A wheel starts from rest and spins with a constant angular acceleration. As time goes on the acceleration vector for a point on the rim:
A) decreases in magnitude and becomes more nearly tangent to the rim
B) decreases in magnitude and becomes more nearly radial
C) increases in magnitude and becomes more nearly tangent to the rim
D) increases in magnitude and becomes more nearly radial
E) increases in magnitude but retains the same angle with the tangent to the rim
A) decreases in magnitude and becomes more nearly tangent to the rim
B) decreases in magnitude and becomes more nearly radial
C) increases in magnitude and becomes more nearly tangent to the rim
D) increases in magnitude and becomes more nearly radial
E) increases in magnitude but retains the same angle with the tangent to the rim

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
45
Four identical particles, each with mass m, are arranged in the x, y plane as shown. They are connected by light sticks to form a rigid body. If m = 2.0 kg and a = 1.0 m, the rotational inertia of this array about the y-axis is: 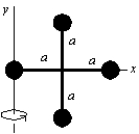
A) 4.0 kg . m2
B) 12 kg.m2
C) 9.6 kg .m2
D) 4.8 kg . m2
E) none of these

A) 4.0 kg . m2
B) 12 kg.m2
C) 9.6 kg .m2
D) 4.8 kg . m2
E) none of these

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
46
A pulley with a radius of 3.0 cm and a rotational inertia of 4.5 *10-3 kg .m2 is suspended from the ceiling. A rope passes over it with a 2.0-kg block attached to one end and a 4.0-kg block attached to the other. The rope does not slip on the pulley. When the velocity of the heavier block is 2.0 m/s the total kinetic energy of the pulley and blocks is:
A) 2.0 J
B) 4.0 J
C) 14 J
D) 22 J
E) 28 J
A) 2.0 J
B) 4.0 J
C) 14 J
D) 22 J
E) 28 J

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
47
The rotational inertia of a solid uniform sphere about a diameter is (2/5)MR2, where M is its mass and R is its radius. If the sphere is pivoted about an axis that is tangent to its surface, its rotational inertia is:
A) MR2
B) (2/5)MR2
C) (3/5)MR2
D) (5/2)MR2
E) (7/5)MR2
A) MR2
B) (2/5)MR2
C) (3/5)MR2
D) (5/2)MR2
E) (7/5)MR2

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
48
A uniform solid cylinder made of lead has the same mass and the same length as a uniform solid cylinder made of wood. The rotational inertia of the lead cylinder compared to the wooden one is:
A) greater
B) less
C) same
D) unknown unless the radii are given
E) unknown unless both the masses and the radii are given
A) greater
B) less
C) same
D) unknown unless the radii are given
E) unknown unless both the masses and the radii are given

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
49
The rotational inertia of a wheel about its axle does not depend upon its:
A) diameter
B) mass
C) distribution of mass
D) speed of rotation
E) material composition
A) diameter
B) mass
C) distribution of mass
D) speed of rotation
E) material composition

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
50
aa

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
50
When a thin uniform stick of mass M and length L is pivoted about its midpoint, its rotational inertia is ML2/12. When pivoted about a parallel axis through one end, its rotational inertia is:
A) ML2/12
B) ML2/6
C) ML2/3
D) 7ML2/12
E) 13ML2/12
A) ML2/12
B) ML2/6
C) ML2/3
D) 7ML2/12
E) 13ML2/12

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
51
aa

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
51
To increase the rotational inertia of a solid disk about its axis without changing its mass:
A) drill holes near the rim and put the material near the axis
B) drill holes near the axis and put the material near the rim
C) drill holes at points on a circle near the rim and put the material at points between the holes
D) drill holes at points on a circle near the axis and put the material at points between the holes
E) do none of the above (the rotational inertia cannot be changed without changing the mass)
A) drill holes near the rim and put the material near the axis
B) drill holes near the axis and put the material near the rim
C) drill holes at points on a circle near the rim and put the material at points between the holes
D) drill holes at points on a circle near the axis and put the material at points between the holes
E) do none of the above (the rotational inertia cannot be changed without changing the mass)

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
52
A solid uniform sphere of radius R and mass M has a rotational inertia about a diameter that is given by (2/5)MR2. A light string of length 3R is attached to the surface and used to suspend the sphere from the ceiling. Its rotational inertia about the point of attachment at the ceiling is:
A) (2/5)MR2
B) 9MR2
C) 16MR2
D) 47/5MR2
E) (82/5)MR2
A) (2/5)MR2
B) 9MR2
C) 16MR2
D) 47/5MR2
E) (82/5)MR2

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
52
aa

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
53
The rotational inertia of a disk about its axis is 0.70 kg . m2. When a 2.0 kg weight is added to its rim, 0.40 m from the axis, the rotational inertia becomes:
A) 0.38 kg . m2
B) 0.54 kg . m2
C) 0.70 kg . m2
D) 0.86 kg . m2
E) 1.0 kg . m2
A) 0.38 kg . m2
B) 0.54 kg . m2
C) 0.70 kg . m2
D) 0.86 kg . m2
E) 1.0 kg . m2

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
54
Three identical balls are tied by light strings to the same rod and rotate around it, as shown below. Rank the balls according to their rotational inertia, least to greatest. 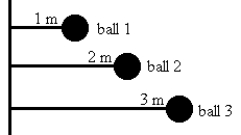
A) 1, 2, 3
B) 3, 2, 1
C) 3, then 1 and 2 tie
D) 1, 3, 2
E) All are the same

A) 1, 2, 3
B) 3, 2, 1
C) 3, then 1 and 2 tie
D) 1, 3, 2
E) All are the same

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
55
Consider four objects, each having the same mass and the same radius:
1. a solid sphere
2. a hollow sphere
3. a flat disk in the x,y plane
4. a hoop in the x,y plane
The order of increasing rotational inertia about an axis through the center of mass and parallel to the z axis is:
A) 1, 2, 3, 4
B) 4, 3, 2, 1
C) 1, 3, 2, 4
D) 4, 2, 3, 1
E) 3, 1, 2, 4
1. a solid sphere
2. a hollow sphere
3. a flat disk in the x,y plane
4. a hoop in the x,y plane
The order of increasing rotational inertia about an axis through the center of mass and parallel to the z axis is:
A) 1, 2, 3, 4
B) 4, 3, 2, 1
C) 1, 3, 2, 4
D) 4, 2, 3, 1
E) 3, 1, 2, 4

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
56
The rotational inertia of a thin cylindrical shell of mass M, radius R, and length L about its central axis (X - X') is: 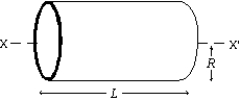
A) MR2/2
B) ML2/2
C) ML2
D) MR2
E) none of these

A) MR2/2
B) ML2/2
C) ML2
D) MR2
E) none of these

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
57
a hoop in the x,y plane The order of increasing rotational inertia about an axis through the center of mass and parallel to the z axis is:
A) 1, 2, 3, 4
B) 4, 3, 2, 1
C) 1, 3, 2, 4
D) 4, 2, 3, 1
E) 3, 1, 2, 4
A) 1, 2, 3, 4
B) 4, 3, 2, 1
C) 1, 3, 2, 4
D) 4, 2, 3, 1
E) 3, 1, 2, 4

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
58
A pulley with a radius of 3.0 cm and a rotational inertia of 4.5 * 10-3 kg .m2 is suspended from the ceiling. A rope passes over it with a 2.0-kg block attached to one end and a 4.0-kg block attached to the other. The rope does not slip on the pulley. At any instant after the blocks start moving the object with the greatest kinetic energy is:
A) the heavier block
B) the lighter block
C) the pulley
D) either block (the two blocks have the same kinetic energy)
E) none (all three objects have the same kinetic energy)
A) the heavier block
B) the lighter block
C) the pulley
D) either block (the two blocks have the same kinetic energy)
E) none (all three objects have the same kinetic energy)

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
59
The meter stick shown below rotates about an axis through the point marked , 20 cm from one end. Five forces act on the stick: one at each end, one at the pivot point, and two 40 cm from one end, as shown. The magnitudes of the forces are all the same. Rank the forces according to the magnitudes of the torques they produce about the pivot point, least to greatest. 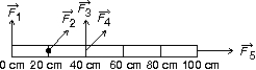
A)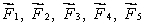
B)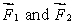 tie, then
tie, then 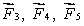
C)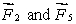 tie, then
tie, then 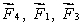
D)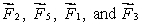 tie, then
tie, then 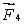
E)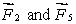 tie, then
tie, then 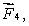 then
then 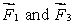 tie
tie

A)
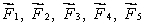
B)
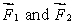 tie, then
tie, then 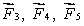
C)
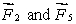 tie, then
tie, then 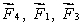
D)
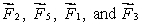 tie, then
tie, then 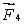
E)
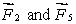 tie, then
tie, then 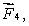 then
then 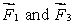 tie
tie
Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
60
Three identical balls, with masses of M, 2M, and 3M are fastened to a massless rod of length L as shown. The rotational inertia about the left end of the rod is: 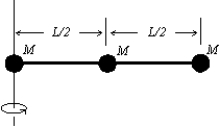
A) ML2/2
B) ML2
C) 3ML2/2
D) 6ML2
E) 3ML2/4

A) ML2/2
B) ML2
C) 3ML2/2
D) 6ML2
E) 3ML2/4

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
61
A block is attached to each end of a rope that passes over a pulley suspended from the ceiling. The blocks do not have the same mass. If the rope does not slip on the pulley, then at any instant after the blocks start moving, the rope:
A) pulls on both blocks, but exerts a greater force on the heavier block
B) pulls on both blocks, but exerts a greater force on the lighter block
C) pulls on both blocks and exerts the same magnitude force on both blocks
D) does not pull on either block
E) pulls only on the lighter block
A) pulls on both blocks, but exerts a greater force on the heavier block
B) pulls on both blocks, but exerts a greater force on the lighter block
C) pulls on both blocks and exerts the same magnitude force on both blocks
D) does not pull on either block
E) pulls only on the lighter block

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
62
A thin circular hoop of mass 1.0 kg and radius 2.0 m is rotating about an axis through its center and perpendicular to its plane. It is slowing down at the rate of 7.0 rad/s2. The net torque acting on it is:
A) 7.0 N . m
B) 14.0 N .m
C) 28.0 N . m
D) 44.0 N . m
E) none of these
A) 7.0 N . m
B) 14.0 N .m
C) 28.0 N . m
D) 44.0 N . m
E) none of these

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
63
A disk with a rotational inertia of 5.0 kg .m2 and a radius of 0.25 m rotates on a frictionless fixed axis perpendicular to the disk and through its center. A force of 8.0 N is applied tangentially to the rim. If the disk starts at rest, then after it has turned through half a revolution its angular velocity is:
A) 0.57 rad/s
B) 0.64 rad/s
C) 0.80 rad/s
D) 1.6 rad/s
E) 3.2 rad/s
A) 0.57 rad/s
B) 0.64 rad/s
C) 0.80 rad/s
D) 1.6 rad/s
E) 3.2 rad/s

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
64
A 16 kg block is attached to a cord that is wrapped around the rim of a flywheel of diameter 0.40 m and hangs vertically, as shown. The rotational inertia of the flywheel is 0.50 kg . m2. When the block is released and the cord unwinds, the acceleration of the block is: 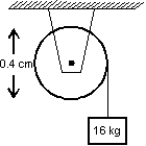
A) 0.15 g
B) 0.56 g
C) 0.84 g
D) g
E) 1.3 g

A) 0.15 g
B) 0.56 g
C) 0.84 g
D) g
E) 1.3 g

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
65
A disk with a rotational inertia of 5.0 kg .m2 and a radius of 0.25 m rotates on a frictionless fixed axis perpendicular to the disk and through its center. A force of 8.0 N is applied along the rotation axis. The angular acceleration of the disk is:
A) 0
B) 0.40 rad/s2
C) 0.60 rad/s2
D) 1.0 rad/s2
E) 2.5 rad/s2
A) 0
B) 0.40 rad/s2
C) 0.60 rad/s2
D) 1.0 rad/s2
E) 2.5 rad/s2

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
66
A disk has a rotational inertia of 6.0 kg .m2 and a constant angular acceleration of 2.0 rad/s2. If it starts from rest the work done during the first 5.0 s by the net torque acting on it is:
A) 0
B) 30 J
C) 60 J
D) 300 J
E) 600 J
A) 0
B) 30 J
C) 60 J
D) 300 J
E) 600 J

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
67
A disk with a rotational inertia of 5.0 kg .m2 and a radius of 0.25 m rotates on a fixed axis perpendicular to the disk and through its center. A force of 2.0 N is applied tangentially to the rim. As the disk turns through half a revolution the work done by the force is:
A) 1.6 J
B) 2.5 J
C) 6.3 J
D) 10 J
E) 40 J
A) 1.6 J
B) 2.5 J
C) 6.3 J
D) 10 J
E) 40 J

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
68
An 8.0-cm radius disk with a rotational inertia of 0.12 kg . m2 is free to rotate on a horizontal axis. A string is fastened to the surface of the disk and a 10-kg mass hangs from the other end. The mass is raised by using a crank to apply a 9.0-N.m torque to the disk. The acceleration of the mass is:
A) 0.50 m/s2
B) 1.7 m/s2
C) 6.2 m/s2
D) 12 m/s2
E) 20 m/s2
A) 0.50 m/s2
B) 1.7 m/s2
C) 6.2 m/s2
D) 12 m/s2
E) 20 m/s2

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
69
A 0.70-kg disk with a rotational inertia given by MR2/2 is free to rotate on a fixed horizontal axis suspended from the ceiling. A string is wrapped around the disk and a 2.0-kg mass hangs from the free end. If the string does not slip then as the mass falls and the cylinder rotates the suspension holding the cylinder pulls up on the cylinder with a force of:
A) 6.9 N
B) 9.8 N
C) 16 N
D) 26 N
E) 29 N
A) 6.9 N
B) 9.8 N
C) 16 N
D) 26 N
E) 29 N

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
70
A disk is free to rotate on a fixed axis. A force of given magnitude F, in the plane of the disk, is to be applied. Of the following alternatives the greatest angular acceleration is obtained if the force is:
A) applied tangentially halfway between the axis and the rim
B) applied tangentially at the rim
C) applied radially halfway between the axis and the rim
D) applied radially at the rim
E) applied at the rim but neither radially nor tangentially
A) applied tangentially halfway between the axis and the rim
B) applied tangentially at the rim
C) applied radially halfway between the axis and the rim
D) applied radially at the rim
E) applied at the rim but neither radially nor tangentially

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
71
A meter stick on a horizontal frictionless table top is pivoted at the 80-cm mark. A horizontal force 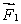 is applied perpendicularly to the end of the stick at 0 cm, as shown. A second horizontal force
is applied perpendicularly to the end of the stick at 0 cm, as shown. A second horizontal force 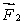 (not shown) is applied at the 100-cm end of the stick. If the stick does not rotate:
(not shown) is applied at the 100-cm end of the stick. If the stick does not rotate: 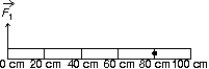
A)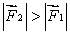 for all orientations of
for all orientations of 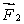
B)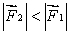 for all orientations of
for all orientations of 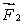
C)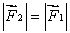 for all orientations of
for all orientations of 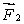
D)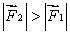 for some orientations of
for some orientations of 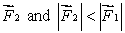 for others
for others
E)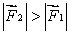 for some orientations of
for some orientations of 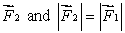 for others
for others
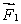 is applied perpendicularly to the end of the stick at 0 cm, as shown. A second horizontal force
is applied perpendicularly to the end of the stick at 0 cm, as shown. A second horizontal force 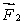 (not shown) is applied at the 100-cm end of the stick. If the stick does not rotate:
(not shown) is applied at the 100-cm end of the stick. If the stick does not rotate: 
A)
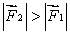 for all orientations of
for all orientations of 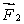
B)
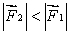 for all orientations of
for all orientations of 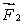
C)
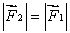 for all orientations of
for all orientations of 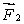
D)
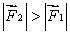 for some orientations of
for some orientations of 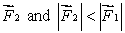 for others
for othersE)
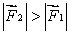 for some orientations of
for some orientations of 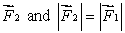 for others
for others
Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
72
A rod is pivoted about its center. A 5-N force is applied 4 m from the pivot and another 5-N force is applied 2 m from the pivot, as shown. The magnitude of the total torque about the pivot (in N.m) is: 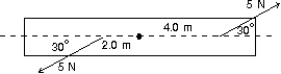
A) 0
B) 5
C) 8.7
D) 15
E) 26

A) 0
B) 5
C) 8.7
D) 15
E) 26

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
73
A uniform disk, a thin hoop, and a uniform sphere, all with the same mass and same outer radius, are each free to rotate about a fixed axis through its center. Assume the hoop is connected to the rotation axis by light spokes. With the objects starting from rest, identical forces are simultaneously applied to the rims, as shown. Rank the objects according the their angular velocities after a given time t, least to greatest. 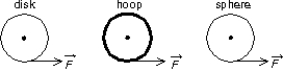
A) disk, hoop, sphere
B) disk, sphere, hoop
C) hoop, sphere, disk
D) hoop, disk, sphere
E) sphere, disk, hoop

A) disk, hoop, sphere
B) disk, sphere, hoop
C) hoop, sphere, disk
D) hoop, disk, sphere
E) sphere, disk, hoop

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
74
A disk with a rotational inertia of 2.0 kg .m2 and a radius of 0.40 m rotates on a frictionless fixed axis perpendicular to the disk faces and through its center. A force of 5.0 N is applied tangentially to the rim. The angular acceleration of the disk is:
A) 0.40 rad/s2
B) 0.60 rad/s2
C) 1.0 rad/s2
D) 2.5 rad/s2
E) 10 rad/s2
A) 0.40 rad/s2
B) 0.60 rad/s2
C) 1.0 rad/s2
D) 2.5 rad/s2
E) 10 rad/s2

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
75
= I for an object rotating about a fixed axis, where is the net torque acting on it, I is its rotational inertia, and is its angular acceleration. This expression:
A) is the definition of torque
B) is the definition of rotational inertia
C) is the definition of angular acceleration
D) follows directly from Newton's second law
E) depends on a principle of physics that is unrelated to Newton's second law
A) is the definition of torque
B) is the definition of rotational inertia
C) is the definition of angular acceleration
D) follows directly from Newton's second law
E) depends on a principle of physics that is unrelated to Newton's second law

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
76
A small disk of radius R1 is fastened coaxially to a larger disk of radius R2. The combination is free to rotate on a fixed axle, which is perpendicular to a horizontal frictionless table top, as shown in the overhead veiw below. The rotational inertia of the combination is I. A string is wrapped around the larger disk and attached to a block of mass m, on the table. Another string is wrapped around the smaller disk and is pulled with a force  as shown. The tension in the string pulling the block is:
as shown. The tension in the string pulling the block is: 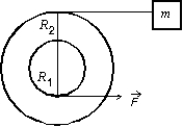
A) R1F/R2
B) mR1R2F/(I - mR22)
C) mR1R2F/(I + mR22)
D) mR1R2F/(I - mR1R 2)
E) mR1R2F/(I + mR1R 2)
 as shown. The tension in the string pulling the block is:
as shown. The tension in the string pulling the block is: 
A) R1F/R2
B) mR1R2F/(I - mR22)
C) mR1R2F/(I + mR22)
D) mR1R2F/(I - mR1R 2)
E) mR1R2F/(I + mR1R 2)

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
77
A small disk of radius R1 is mounted coaxially with a larger disk of radius R2. The disks are securely fastened to each other and the combination is free to rotate on a fixed axle that is perpendicular to a horizontal frictionless table top,as shown in the overhead veiw below. The rotational inertia of the combination is I. A string is wrapped around the larger disk and attached to a block of mass m, on the table. Another string is wrapped around the smaller disk and is pulled with a force 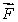 as shown. The acceleration of the block is:
as shown. The acceleration of the block is: 
A) R1F/mR2
B) R1R2F/(I - mR2 2)
C) R1R2F/(I + mR2 2)
D) R1R2F/(I - mR1R 2)
E) R1R2F/(I + mR1R 2)
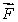 as shown. The acceleration of the block is:
as shown. The acceleration of the block is: 
A) R1F/mR2
B) R1R2F/(I - mR2 2)
C) R1R2F/(I + mR2 2)
D) R1R2F/(I - mR1R 2)
E) R1R2F/(I + mR1R 2)

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck


