Deck 12: Equilibrium and Elasticity
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/53
Play
Full screen (f)
Deck 12: Equilibrium and Elasticity
1
For a body to be equilibrium under the combined action of several forces:
A) all the forces must be applied at the same point
B) all of the forces are composed of pairs of equal and opposite forces
C) any two of these forces must be balanced by a third force
D) the sum of the torques about any point must equal zero
E) the lines of action of all the forces must pass through the center of gravity of the body
A) all the forces must be applied at the same point
B) all of the forces are composed of pairs of equal and opposite forces
C) any two of these forces must be balanced by a third force
D) the sum of the torques about any point must equal zero
E) the lines of action of all the forces must pass through the center of gravity of the body
the sum of the torques about any point must equal zero
2
A picture P of weight W is hung by two strings as shown. The magnitude of the tension force of each string is T. The total upward pull of the strings on the picture is: 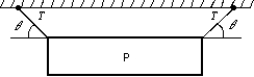
A) 2W cos
B) T sin
C) T cos
D) 2T sin
E) 2T cos

A) 2W cos
B) T sin
C) T cos
D) 2T sin
E) 2T cos
2T sin
3
For a body to be equilibrium under the combined action of several forces:
A) all the forces must be applied at the same point
B) all of the forces are composed of pairs of equal and opposite forces
C) the sum of the components of all the forces in any direction must equal zero
D) any two of these forces must be balanced by a third force
E) the lines of action of all the forces must pass through the center of gravity of the body
A) all the forces must be applied at the same point
B) all of the forces are composed of pairs of equal and opposite forces
C) the sum of the components of all the forces in any direction must equal zero
D) any two of these forces must be balanced by a third force
E) the lines of action of all the forces must pass through the center of gravity of the body
the sum of the components of all the forces in any direction must equal zero
4
The conditions that the sum of forces and the sum of the torques both vanish:
A) hold for every solid body in equilibrium
B) hold only for elastic solid bodies in equilibrium
C) hold for every solid body
D) are always sufficient to calculate the forces on a solid object in equilibrium
E) are sufficient to calculate the forces on a solid object in equilibrium only if the object is elastic
A) hold for every solid body in equilibrium
B) hold only for elastic solid bodies in equilibrium
C) hold for every solid body
D) are always sufficient to calculate the forces on a solid object in equilibrium
E) are sufficient to calculate the forces on a solid object in equilibrium only if the object is elastic

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
5
A cube balanced with one edge in contact with a table top and with its center of gravity directly above the edge is in ________ equilibrium with respect to rotation about the edge and in ________ equilibrium with respect to rotation about a horizontal axis that is perpendicular to the edge.
A) stable, stable
B) stable, unstable
C) unstable, stable
D) unstable, unstable
E) unstable, neutral
A) stable, stable
B) stable, unstable
C) unstable, stable
D) unstable, unstable
E) unstable, neutral

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
6
To determine if a rigid body is in equilibrium the vector sum of the gravitational forces acting on the particles of the body can be replaced by a single force acting at:
A) the center of mass
B) the geometrical center
C) the center of gravity
D) a point on the boundary
E) none of the above
A) the center of mass
B) the geometrical center
C) the center of gravity
D) a point on the boundary
E) none of the above

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
7
A uniform plank XY is supported by two equal 120-N forces at X and Y, as shown. The support at X is then moved to Z (half-way to the plank center). The supporting forces at Y and Z are then: 
A) FY = 240 N, FZ = 120 N
B) FY = 200 N, FZ = 40 N
C) FY = 40 N, FZ = 200 N
D) FY = 80 N, FZ = 160 N
E) FY = 160 N, FZ = 80 N

A) FY = 240 N, FZ = 120 N
B) FY = 200 N, FZ = 40 N
C) FY = 40 N, FZ = 200 N
D) FY = 80 N, FZ = 160 N
E) FY = 160 N, FZ = 80 N

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
8
A meter stick on a horizontal frictionless table top is pivoted at the 80-cm mark. A force  is applied perpendicularly to the end of the stick at 0 cm, as shown. A second force
is applied perpendicularly to the end of the stick at 0 cm, as shown. A second force  (not shown) is applied perpendicularly at the 100-cm end of the stick. The forces are horizontal. If the stick does not move, the force exerted by the pivot on the stick:
(not shown) is applied perpendicularly at the 100-cm end of the stick. The forces are horizontal. If the stick does not move, the force exerted by the pivot on the stick: 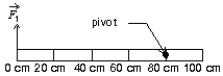
A) must be zero
B) must be in the same direction as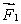 and have magnitude
and have magnitude 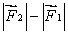
C) must be directed opposite to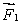 and have magnitude
and have magnitude 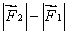
D) must be in the same direction as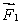 and have magnitude
and have magnitude 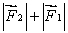
E) must be directed opposite to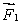 and have magnitude
and have magnitude 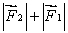
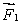 is applied perpendicularly to the end of the stick at 0 cm, as shown. A second force
is applied perpendicularly to the end of the stick at 0 cm, as shown. A second force 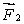 (not shown) is applied perpendicularly at the 100-cm end of the stick. The forces are horizontal. If the stick does not move, the force exerted by the pivot on the stick:
(not shown) is applied perpendicularly at the 100-cm end of the stick. The forces are horizontal. If the stick does not move, the force exerted by the pivot on the stick: 
A) must be zero
B) must be in the same direction as
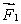 and have magnitude
and have magnitude 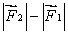
C) must be directed opposite to
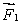 and have magnitude
and have magnitude 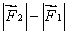
D) must be in the same direction as
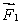 and have magnitude
and have magnitude 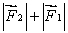
E) must be directed opposite to
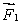 and have magnitude
and have magnitude 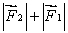

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
9
A cylinder placed so it can roll on a horizontal table top, with its center of gravity above its geometrical center, is:
A) in stable equilibrium
B) in unstable equilibrium
C) in neutral equilibrium
D) not in equilibrium
E) none of the above
A) in stable equilibrium
B) in unstable equilibrium
C) in neutral equilibrium
D) not in equilibrium
E) none of the above

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
10
The center of gravity coincides with the center of mass:
A) always
B) never
C) if the center of mass is at the geometrical center of the body
D) if the acceleration due to gravity is uniform over the body
E) if the body has a uniform distribution of mass
A) always
B) never
C) if the center of mass is at the geometrical center of the body
D) if the acceleration due to gravity is uniform over the body
E) if the body has a uniform distribution of mass

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
11
The diagram shows a stationary 5-kg uniform rod (AC), 1 m long, held against a wall by a rope (AE) and friction between the rod and the wall. To use a single equation to find the force exerted on the rod by the rope at which point should you place the reference point for computing torque? 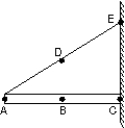
A) A
B) B
C) C
D) D
E) E

A) A
B) B
C) C
D) D
E) E

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
12
Three identical uniform rods are each acted on by two or more forces, all perpendicular to the rods. Which of the rods could be in static equilibrium if an additional force is applied at the center of mass of the rod? 
A) Only 1
B) Only 2
C) Only 3
D) Only 1 and 2
E) All three

A) Only 1
B) Only 2
C) Only 3
D) Only 1 and 2
E) All three

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
13
The location of which of the following points within an object might depend on the orientation of the object?
A) Its center of mass
B) Its center of gravity
C) Its geometrical center
D) Its center of momentum
E) None of the above
A) Its center of mass
B) Its center of gravity
C) Its geometrical center
D) Its center of momentum
E) None of the above

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
14
A meter stick on a horizontal frictionless table top is pivoted at the 80-cm mark. A force 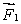 is applied perpendicularly to the end of the stick at 0 cm, as shown. A second force
is applied perpendicularly to the end of the stick at 0 cm, as shown. A second force 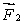 (not shown) is applied perpendicularly at the 60-cm mark. The forces are horizontal. If the stick does not move, the force exerted by the pivot on the stick:
(not shown) is applied perpendicularly at the 60-cm mark. The forces are horizontal. If the stick does not move, the force exerted by the pivot on the stick: 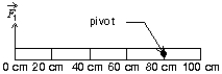
A) must be zero
B) must be in the same direction as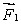 and have magnitude
and have magnitude 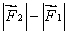
C) must be directed opposite to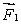 and have magnitude
and have magnitude 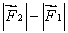
D) must be in the same direction as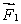 and have magnitude
and have magnitude 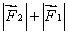
E) must be directed opposite to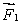 and have magnitude
and have magnitude 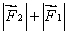
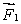 is applied perpendicularly to the end of the stick at 0 cm, as shown. A second force
is applied perpendicularly to the end of the stick at 0 cm, as shown. A second force 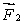 (not shown) is applied perpendicularly at the 60-cm mark. The forces are horizontal. If the stick does not move, the force exerted by the pivot on the stick:
(not shown) is applied perpendicularly at the 60-cm mark. The forces are horizontal. If the stick does not move, the force exerted by the pivot on the stick: 
A) must be zero
B) must be in the same direction as
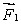 and have magnitude
and have magnitude 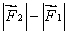
C) must be directed opposite to
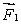 and have magnitude
and have magnitude 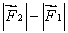
D) must be in the same direction as
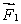 and have magnitude
and have magnitude 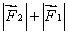
E) must be directed opposite to
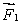 and have magnitude
and have magnitude 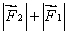

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
15
A cylinder placed so it can roll on a horizontal table top, with its center of gravity below its geometrical center, is:
A) in stable equilibrium
B) in unstable equilibrium
C) in neutral equilibrium
D) not in equilibrium
E) none of the above
A) in stable equilibrium
B) in unstable equilibrium
C) in neutral equilibrium
D) not in equilibrium
E) none of the above

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
16
A net torque applied to a rigid object always tends to produce:
A) linear acceleration
B) rotational equilibrium
C) angular acceleration
D) rotational inertia
E) none of these
A) linear acceleration
B) rotational equilibrium
C) angular acceleration
D) rotational inertia
E) none of these

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
17
A picture can be hung on a wall in three different ways, as shown. The tension in the string is: 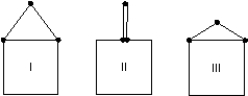
A) least in I
B) greatest in I
C) greatest in II
D) least in III
E) greatest in III

A) least in I
B) greatest in I
C) greatest in II
D) least in III
E) greatest in III

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
18
A 160-N child sits on a light swing and is pulled back and held with a horizontal force of 100 N. The magnitude of the tension force of each of the two supporting ropes is:
A) 60 N
B) 94 N
C) 120 N
D) 190 N
E) 260 N
A) 60 N
B) 94 N
C) 120 N
D) 190 N
E) 260 N

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
19
A uniform rod AB is 1.2 m long and weighs 16 N. It is suspended by strings AC and BD as shown. A block P weighing 96 N is attached at E, 0.30 m from A. The magnitude of the tension force in the string BD is: 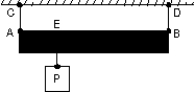
A) 8.0 N
B) 24 N
C) 32 N
D) 48 N
E) 80 N

A) 8.0 N
B) 24 N
C) 32 N
D) 48 N
E) 80 N

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
20
For an object in equilibrium the sum of the torques acting on it vanishes only if each torque is calculated about:
A) the center of mass
B) the center of gravity
C) the geometrical center
D) the point of application of the force
E) the same point
A) the center of mass
B) the center of gravity
C) the geometrical center
D) the point of application of the force
E) the same point

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
21
Strain can be measured in:
A) N/m2
B) N.m2
C) N/m
D) N.m
E) none of these (it is unitless)
A) N/m2
B) N.m2
C) N/m
D) N.m
E) none of these (it is unitless)

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
22
The 600-N ball shown is suspended on a string AB and rests against the frictionless vertical wall. The string makes an angle of 30 with the wall. The magnitude of the tension for of string is: 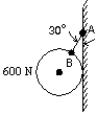
A) 690 N
B) 1200 N
C) 2100 N
D) 2400 N
E) none of these

A) 690 N
B) 1200 N
C) 2100 N
D) 2400 N
E) none of these

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
23
A 960-N block is suspended as shown. The beam AB is weightless and is hinged to the wall at A. The tension force of the cable BC has magnitude: 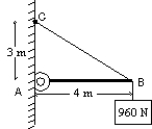
A) 720 N
B) 1200 N
C) 1280 N
D) 1600 N
E) none of these

A) 720 N
B) 1200 N
C) 1280 N
D) 1600 N
E) none of these

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
24
An 80-N uniform plank leans against a frictionless wall as shown. The torque (about point P) applied to the plank by the wall is: 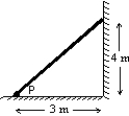
A) 40 N.m
B) 60 N.m
C) 120 N.m
D) 160 N.m
E) 240 N.m

A) 40 N.m
B) 60 N.m
C) 120 N.m
D) 160 N.m
E) 240 N.m

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
25
A uniform ladder is 10 cm long and weighs 400 N. It rests with its upper end against a frictionless vertical wall. Its lower end rests on the ground and is prevented from slipping by a peg driven into the ground. The ladder makes a 30 angle with the horizontal. The force exerted on the wall by the ladder is: 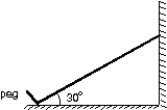
A) 48 N
B) 74 N
C) 120 N
D) 350 N
E) 610 N

A) 48 N
B) 74 N
C) 120 N
D) 350 N
E) 610 N

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
26
A uniform 240-g meter stick can be balanced by a 240-g weight placed at the 100-cm mark if the fulcrum is placed at the point marked:
A) 75 cm
B) 60 cm
C) 50 cm
D) 40 cm
E) 80 cm
A) 75 cm
B) 60 cm
C) 50 cm
D) 40 cm
E) 80 cm

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
27
A window washer attempts to lean a ladder against a frictionless wall. He finds that the ladder slips on the ground when it is placed at an angle of less than 75 to the ground but remains in place when the angle is greater than 75 . The coefficient of static friction between the ladder and the ground:
A) is about 0.13
B) is about 0.27
C) is about 1.3
D) depends on the mass of the ladder
E) depends on the length of the ladder
A) is about 0.13
B) is about 0.27
C) is about 1.3
D) depends on the mass of the ladder
E) depends on the length of the ladder

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
28
The ideal mechanical advantage (i.e. the ratio of the weight W to the pull P for equilibrium) of the combination of pulleys shown is: 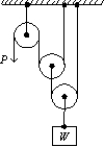
A) 1
B) 2
C) 3
D) 4
E) 5

A) 1
B) 2
C) 3
D) 4
E) 5

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
29
An 800-N man stands halfway up a 5.0 m ladder of negligible weight. The base of the ladder is 3.0 m from the wall as shown. Assuming that the wall-ladder contact is frictionless, the wall pushes against the ladder with a force of: 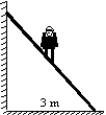
A) 150 N
B) 300 N
C) 400 N
D) 600 N
E) 800 N

A) 150 N
B) 300 N
C) 400 N
D) 600 N
E) 800 N

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
30
The pull P is just sufficient to keep the 14-N block and the weightless pulleys in equilibrium as shown. The tension T in the upper cable is: 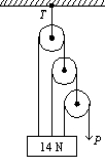
A) 14 N
B) 28 N
C) 16 N
D) 9.33 N
E) 18.7 N

A) 14 N
B) 28 N
C) 16 N
D) 9.33 N
E) 18.7 N

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
31
A 5.0 m weightless strut, hinged to a wall, is used to support a 800-N block as shown. The horizontal and vertical components of the force of the hinge on the strut are: 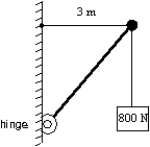
A) FH = 800 N, FY = 800 N
B) FH = 600 N, FY = 800 N
C) FH = 800 N, FY = 600 N
D) FH = 1200 N, FY = 800 N
E) FH = 0 , FY = 800 N

A) FH = 800 N, FY = 800 N
B) FH = 600 N, FY = 800 N
C) FH = 800 N, FY = 600 N
D) FH = 1200 N, FY = 800 N
E) FH = 0 , FY = 800 N

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
32
A horizontal beam of weight W is supported by a hinge and cable as shown. The force exerted on the beam by the hinge has a vertical component that must be: 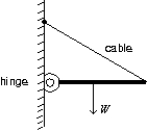
A) nonzero and up
B) nonzero and down
C) nonzero but not enough information given to know whether up or down
D) zero
E) equal to W

A) nonzero and up
B) nonzero and down
C) nonzero but not enough information given to know whether up or down
D) zero
E) equal to W

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
33
The uniform rod shown below is held in place by the rope and wall. Suppose you know the weight of the rod and all dimensions. Then you can solve a single equation for the force exerted by the rope, provided you write expressions for the torques about the point: 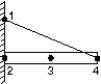
A) 1
B) 2
C) 3
D) 4
E) 1, 2, or 3

A) 1
B) 2
C) 3
D) 4
E) 1, 2, or 3

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
34
A 400-N uniform vertical boom is attached to the ceiling by a hinge, as shown. An 800-N weight W and a horizontal guy wire are attached to the lower end of the boom as indicated. The pulley is massless and frictionless. The tension force T of the horizontal guy wire has magnitude: 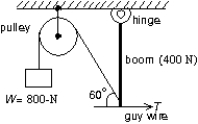
A) 340 N
B) 400 N
C) 690 N
D) 800 N
E) 1200 N

A) 340 N
B) 400 N
C) 690 N
D) 800 N
E) 1200 N

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
35
A ladder leans against a wall. If the ladder is not to slip, which one of the following must be true? 
A) The coefficient of friction between the ladder and the wall must not be zero
B) The coefficient of friction between the ladder and the floor must not be zero
C) Both A and B
D) Either A or B
E) Neither A nor B

A) The coefficient of friction between the ladder and the wall must not be zero
B) The coefficient of friction between the ladder and the floor must not be zero
C) Both A and B
D) Either A or B
E) Neither A nor B

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
36
The 600-N ball shown is suspended on a string AB and rests against the frictionless vertical wall. The string makes an angle of 30 with the wall. The ball presses against the wall with a force of magnitude: 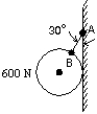
A) 120 N
B) 300 N
C) 350 N
D) 600 N
E) 690 N

A) 120 N
B) 300 N
C) 350 N
D) 600 N
E) 690 N

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
37
A 240-N weight is hung from two ropes as shown. The tension in the horizontal rope has magnitude: 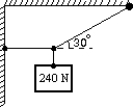
A) 0
B) 656 N
C) 480 N
D) 416 N
E) 176 N

A) 0
B) 656 N
C) 480 N
D) 416 N
E) 176 N

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
38
A picture is to be hung from the ceiling by means of two wires. Order the following arrangements of the wires according to the tension in wire B, from least to greatest. 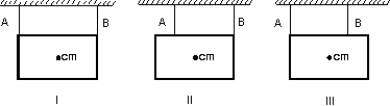
A) I, II, III
B) III, II, I
C) I and II tie, then III
D) II, I, III
E) all tie

A) I, II, III
B) III, II, I
C) I and II tie, then III
D) II, I, III
E) all tie

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
39
Stress can be measured in:
A) N/m2
B) N.m2
C) N/m
D) N.m
E) none of these (it is unitless)
A) N/m2
B) N.m2
C) N/m
D) N.m
E) none of these (it is unitless)

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
40
A uniform plank is 6.0 m long and weighs 80 N. It is balanced on a sawhorse at its center. An additional 160 N weight is now placed on the left end of the plank. To keep the plank balanced, it must be moved what distance to the right?
A) 6.0 m
B) 2.0 m
C) 1.5 m
D) 1.0 m
E) 0.50 m
A) 6.0 m
B) 2.0 m
C) 1.5 m
D) 1.0 m
E) 0.50 m

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
41
To shear a cube-shaped object, forces of equal magnitude and opposite directions might be applied:
A) to opposite faces, perpendicular to the faces
B) to opposite faces, parallel to the faces
C) to adjacent faces, perpendicular to the faces
D) to adjacent faces, neither parallel or perpendicular to the faces
E) to a single face, in any direction
A) to opposite faces, perpendicular to the faces
B) to opposite faces, parallel to the faces
C) to adjacent faces, perpendicular to the faces
D) to adjacent faces, neither parallel or perpendicular to the faces
E) to a single face, in any direction

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
42
Young's modulus is a proportionality constant that relates the force per unit area applied perpendicularly at the surface of an object to:
A) the shear
B) the fractional change in volume
C) the fractional change in length
D) the pressure
E) the spring constant
A) the shear
B) the fractional change in volume
C) the fractional change in length
D) the pressure
E) the spring constant

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
43
The bulk modulus is a proportionality constant that relates the pressure acting on an object to:
A) the shear
B) the fractional change in volume
C) the fractional change in length
D) Young's modulus
E) the spring constant
A) the shear
B) the fractional change in volume
C) the fractional change in length
D) Young's modulus
E) the spring constant

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
44
Young's modulus can be used to calculate the strain for a stress that is:
A) just below the ultimate strength
B) just above the ultimate strength
C) well below the yield strength
D) well above the yield strength
E) none of the above
A) just below the ultimate strength
B) just above the ultimate strength
C) well below the yield strength
D) well above the yield strength
E) none of the above

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
45
The ultimate strength of a sample is the stress at which the sample:
A) returns to its original shape when the stress is removed
B) remains underwater
C) breaks
D) bends 180
E) does none of these
A) returns to its original shape when the stress is removed
B) remains underwater
C) breaks
D) bends 180
E) does none of these

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
46
A certain wire stretches 0.90 cm when outward forces with magnitude F are applied to each end. The same forces are applied to a wire of the same material but with three times the diameter and three times the length. The second wire stretches:
A) 0.10 cm
B) 0.30 cm
C) 0.90 cm
D) 2.7 cm
E) 8.1 cm
A) 0.10 cm
B) 0.30 cm
C) 0.90 cm
D) 2.7 cm
E) 8.1 cm

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
47
Young's modulus can be correctly given in:
A) N.m
B) N.m2
C) N.m/s
D) N/m
E) joules
A) N.m
B) N.m2
C) N.m/s
D) N/m
E) joules

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
48
A 4.0 m steel beam with a cross sectional area of 1.0 *10-2 m2 and a Young's modulus of 2.0 * 1011 N/m2 is wedged horizontally between two vertical walls. In order to wedge the beam, it is compressed by 0.020 mm. If the coefficient of static friction between the beam and the walls is 0.70, the maximum mass (including its own) it can bear without slipping is:
A) 0
B) 3.6 kg
C) 36 kg
D) 71 kg
E) 710 kg
A) 0
B) 3.6 kg
C) 36 kg
D) 71 kg
E) 710 kg

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
49
A cube with edges exactly 2 cm long is made of material with a bulk modulus of 3.5 * 109 N/m2. When it is subjected to a pressure of 3.0 *105 Pa its volume is:
A) 7.31 cm3
B) 7.99931 cm3
C) 8.00069 cm3
D) 8.69 cm3
E) none of these
A) 7.31 cm3
B) 7.99931 cm3
C) 8.00069 cm3
D) 8.69 cm3
E) none of these

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
50
Two supports, made of the same material and initially of equal length, are 2.0 m apart. A stiff board with a length of 4.0 m and a mass of 10 kg is placed on the supports, with one support at the left end and the other at the midpoint. A block is placed on the board a distance of 0.50 m from left end.As a result the board is horizontal. The mass of the block is:
A) zero
B) 2.3 kg
C) 6.6 kg
D) 10 kg
E) 20 kg
A) zero
B) 2.3 kg
C) 6.6 kg
D) 10 kg
E) 20 kg

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
51
A force of 5000 N is applied outwardly to each end of a 5.0-m long rod with a radius of 34.0 cm and a Young's modulus of 125 * 108 N/m2. The elongation of the rod is:
A) 0.0020 mm
B) 0.0040 mm
C) 0.14 mm
D) 0.55 mm
E) 1.42 mm
A) 0.0020 mm
B) 0.0040 mm
C) 0.14 mm
D) 0.55 mm
E) 1.42 mm

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
52
A shearing force of 50 N is applied to an aluminum rod with a length of 10 m, a cross-sectional area of 1.0 *10-5 m, and shear modulus of 2.5 *1010N/m2. As a result the rod is sheared through a distance of:
A) zero
B) 1.9 mm
C) 1.9 cm
D) 19 cm
E) 1.9 m
A) zero
B) 1.9 mm
C) 1.9 cm
D) 19 cm
E) 1.9 m

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
53
A cube with 2.0-cm sides is made of material with a bulk modulus of 4.7 * 105 N/m2. When it is subjected to a pressure of 2.0 *105 Pa the length in cm of its any of its any of its sides is:
A) 0.85 cm
B) 1.15 cm
C) 1.66 cm
D) 2.0 cm
E) none of these
A) 0.85 cm
B) 1.15 cm
C) 1.66 cm
D) 2.0 cm
E) none of these

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck


