Deck 22: Markov Analysis
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/64
Play
Full screen (f)
Deck 22: Markov Analysis
1
If a Markov process contains an absorbing state, the process will eventually terminate in the absorbing state.
True
2
Markov analysis is not an optimization technique.
True
3
A Markov assumption is that the probabilities apply to all system participants.
True
4
Markov analysis is a probabilistic technique.

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
5
Decision trees can be used to solve for steady state probabilities.

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
6
A Markov assumption is that the probabilities are constant over time.

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
7
Markov analysis is not a probabilistic technique.

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
8
Markov analysis provides a recommended decision.

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
9
Markov analysis can be used to determine the steady state probabilities associated with machine breakdowns.

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
10
Markov Analysis always results in a steady state.

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
11
A transition matrix cannot cause the system to cycle between states.

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
12
Markov analysis does not provide a recommended decision.

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
13
A Markov assumption is that the probabilities change over time.

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
14
A Markov assumption is that the probabilities in each row sum to 1 because they are mutually exclusive and collectively exhaustive.

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
15
The brand-switching problem analyzes the probability of customers' changing brands of a product over time.

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
16
Markov analysis provides information on the probability of customers switching from one brand to one or more other brands.

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
17
Markov analysis is a descriptive technique that results in probabilistic information.

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
18
Markov analysis is not a descriptive technique that results in probabilistic information.

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
19
Markov analysis is an optimization technique.

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
20
The state of the system is where the system is at a point in time.

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
21
The only car dealership in a community stocks cars from two manufacturers, Fret and Cessy. The following transition matrix shows the probabilities of a customer purchasing each brand of car in the next year given that he or she purchased that car in the current year. 
Given that a customer purchased the brand Cessy in the present year (year 1), determine the probability that a customer will purchase Fret in year 3.

Given that a customer purchased the brand Cessy in the present year (year 1), determine the probability that a customer will purchase Fret in year 3.

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
22
A ________ is the probability of moving from one state to another during one time period.

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
23
A Markov process has the following transition matrix:
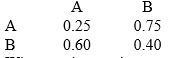 What are the steady state probabilities?
What are the steady state probabilities?
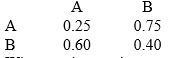 What are the steady state probabilities?
What are the steady state probabilities?
Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
24
Markov analysis is a ________ technique.

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
25
Steady state probabilities can be computed by developing a set of equations using ________ operations and solving them simultaneously.

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
26
The only car dealership in a community stocks cars from two manufacturers, Fret and Cessy. The following transition matrix shows the probabilities of a customer purchasing each brand of car in the next year given that he or she purchased that car in the current year. 
Given that a customer purchased the brand Fret in the present year (year 1), determine the probability that a customer will purchase Cessy in year 3.

Given that a customer purchased the brand Fret in the present year (year 1), determine the probability that a customer will purchase Cessy in year 3.

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
27
A Markov process has the following transition matrix:
 What are the steady state probabilities?
What are the steady state probabilities?
 What are the steady state probabilities?
What are the steady state probabilities?
Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
28
In certain applications, the transition matrix may first need to be divided into submatrices. The identity matrix, I, and matrix Q (the nonabsorbing matrix) are then used to determine the ________ matrix.

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
29
A common application of Markov analysis is ________.

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
30
A Markov process has the following transition matrix:
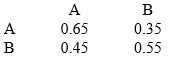 What are the steady state probabilities?
What are the steady state probabilities?
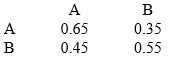 What are the steady state probabilities?
What are the steady state probabilities?
Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
31
In Markov analysis, once the system leaves a(n) ________ state, it will never return.

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
32
In Markov analysis, once the system moves into a(n) ________ state, it is trapped and cannot leave.

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
33
A Markov process for two states has the following transition matrix:

Assume that we start with state 1, what is the probability matrix of the system being in state A or B in period 3 given the system started in state B?

Assume that we start with state 1, what is the probability matrix of the system being in state A or B in period 3 given the system started in state B?

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
34
Although information from Markov analysis can be obtained using a ________, it is time-consuming and cumbersome.

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
35
________ probabilities are average constant probabilities that the system will be in a state in the future.

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
36
The probability of ending up in a state in the future is ________ of the starting state.

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
37
An assumption of Markov analysis is that the probability of moving from a state to all other states sum to ________.

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
38
A transition matrix is ________ when it moves back and forth between states.

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
39
An assumption of Markov analysis is that the probabilities are ________ over time.

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
40
A Markov assumption is that the probabilities in each row sum to ________ because they are mutually exclusive and collectively exhaustive.

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
41
Limmer's is going to launch a new advertising campaign in order to attract new customers. The "before" and "after" transition matrices are shown below:
Before: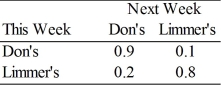
After: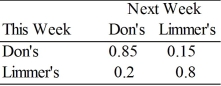
If there are 1000 customers who shop at these two stores, how many customers, over the long run, will switch to Limmer's as a result of the new campaign?
Before:

After:

If there are 1000 customers who shop at these two stores, how many customers, over the long run, will switch to Limmer's as a result of the new campaign?

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
42
The only car dealership in a community stocks cars from two manufacturers, Fret and Cessy. The following transition matrix shows the probabilities of a customer purchasing each brand of car in the next year given that he or she purchased that car in the current year. 
Given that a customer purchased the brand Cessy in the present year (year 1), determine the probability that a customer will purchase Cessy in year 3.

Given that a customer purchased the brand Cessy in the present year (year 1), determine the probability that a customer will purchase Cessy in year 3.

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
43
The ________ is average, constant probability that the system will be in a state in the future.
A) transition probability
B) state of the system
C) steady-state probability
D) transition matrix
A) transition probability
B) state of the system
C) steady-state probability
D) transition matrix

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
44
For the following transition matrices, what is the absorbing state(s)?
A) state 1
B) state 2
C) state 3
D) state 4
E) state 2 and 4
A) state 1
B) state 2
C) state 3
D) state 4
E) state 2 and 4

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
45
A Markov assumption is that the probabilities apply to ________ system participants.
A) none of the
B) the major
C) some
D) all
A) none of the
B) the major
C) some
D) all

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
46
The ________ is the probability of moving from one state to another during one time period.
A) transition probability
B) state of the system
C) steady-state probabilities
D) transition matrix
A) transition probability
B) state of the system
C) steady-state probabilities
D) transition matrix

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
47
The ________ is where the system is at a point in time.
A) transition probability
B) state of the system
C) steady-state probabilities
D) transition matrix
A) transition probability
B) state of the system
C) steady-state probabilities
D) transition matrix

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
48
The transition matrix below shows the probabilities that customer switch between two grocery stores, Don's and Limmer's, each week. 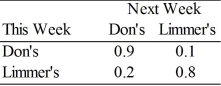
If there are 2000 customers who shop at either store, how many over the long run would shop at Limmer's?

If there are 2000 customers who shop at either store, how many over the long run would shop at Limmer's?

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
49
The transition matrix below shows the probabilities that customer switch between two grocery stores, Don's and Limmer's, each week. If a customer shopped at Don's the first week, what is the probability that they are shopping at Limmer's the third week?
A) 0.17
B) 0.34
C) 0.66
D) 0.83
E) none of the above
A) 0.17
B) 0.34
C) 0.66
D) 0.83
E) none of the above

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
50
A Markov assumption is that the probabilities in each row sum to 1 because they are
A) mutually exclusive.
B) collectively exhaustive.
C) mutually exclusive and collectively exhaustive.
D) mutually exclusive or collectively exhaustive.
A) mutually exclusive.
B) collectively exhaustive.
C) mutually exclusive and collectively exhaustive.
D) mutually exclusive or collectively exhaustive.

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
51
Participants eligible for a retraining program can be in one of four states:
A - not in the training program
B - discharged
C - in training
D - employed
You are given the following transition matrix and the fundamental matrix.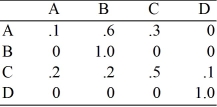
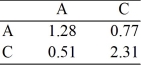
Assume that there were initially 10 people not in the training program (State
A) and 60 people who were in the training program (State
C). How many people will end up being discharged, and how many people will be employed?
A - not in the training program
B - discharged
C - in training
D - employed
You are given the following transition matrix and the fundamental matrix.


Assume that there were initially 10 people not in the training program (State
A) and 60 people who were in the training program (State
C). How many people will end up being discharged, and how many people will be employed?

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
52
Markov analysis is a ________ technique that results in ________ information.
A) descriptive, descriptive
B) probabilistic, descriptive
C) descriptive, probabilistic
D) probabilistic, probabilistic
A) descriptive, descriptive
B) probabilistic, descriptive
C) descriptive, probabilistic
D) probabilistic, probabilistic

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
53
The only car dealership in a community stocks cars from two manufacturers, Fret and Cessy. The following transition matrix shows the probabilities of a customer purchasing each brand of car in the next year given that he or she purchased that car in the current year. 
Determine the steady state probabilities for Fret and Cessy.

Determine the steady state probabilities for Fret and Cessy.

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
54
A Markov assumption is that the probabilities ________ over time.
A) become smaller
B) become larger
C) change
D) are constant
A) become smaller
B) become larger
C) change
D) are constant

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
55
Markov analysis ________ a recommended decision.
A) does not provide
B) always provides
C) sometimes provides
D) rarely provides
A) does not provide
B) always provides
C) sometimes provides
D) rarely provides

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
56
Participants eligible for a retraining program can be in one of four states:
A - not in the training program
B - discharged
C - in training
D - employed
Given the following transition matrix, determine the fundamental matrix.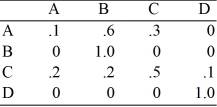
A - not in the training program
B - discharged
C - in training
D - employed
Given the following transition matrix, determine the fundamental matrix.


Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
57
For the following transition matrices, determine the transient or absorbing states. 


Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
58
For the following transition matrices, determine the transient or absorbing states. 


Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
59
The only car dealership in a community stocks cars from two manufacturers, Fret and Cessy. The following transition matrix shows the probabilities of a customer purchasing each brand of car in the next year given that he or she purchased that car in the current year. Given that a customer purchased the brand Fret in the present year (year 1), determine the probability that a customer will purchase Cessy in year 3.
A) .7
B) .61
C) .39
D) .21
E) .18
A) .7
B) .61
C) .39
D) .21
E) .18

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
60
Which of the following is not an assumption or a characteristic of a Markov Process?
A) The transition probabilities are the same for any customer.
B) The transition probabilities will remain constant over time.
C) The probability of being in a particular state at any one time period depends only on the state immediately preceding it.
D) In a transition matrix, sum of the row probabilities must sum to one.
E) In a transition matrix, sum of the column probabilities must sum to one.
A) The transition probabilities are the same for any customer.
B) The transition probabilities will remain constant over time.
C) The probability of being in a particular state at any one time period depends only on the state immediately preceding it.
D) In a transition matrix, sum of the row probabilities must sum to one.
E) In a transition matrix, sum of the column probabilities must sum to one.

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
61
Participants eligible for a retraining program can be in one of four states:
A - not in the training program
B - discharged
C - in training
D - employed
You are given the following transition matrix and the fundamental matrix.
Assume that there were initially 10 people not in the training program (State A) and 60 people who were in the training program (State C). Approximately how many people will be employed?
A) 10
B) 15
C) 40
D) 55
E) 60
A - not in the training program
B - discharged
C - in training
D - employed
You are given the following transition matrix and the fundamental matrix.
Assume that there were initially 10 people not in the training program (State A) and 60 people who were in the training program (State C). Approximately how many people will be employed?
A) 10
B) 15
C) 40
D) 55
E) 60

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
62
The only car dealership in a community stocks cars from two manufacturers, Fret and Cessy. The following transition matrix shows the probabilities of a customer purchasing each brand of car in the next year given that he or she purchased that car in the current year. Determine the steady state probabilities for Fret and Cessy.
A) .875, .125
B) .645, .355
C) .621, .379
D) .571, .429
E).55, .45
A) .875, .125
B) .645, .355
C) .621, .379
D) .571, .429
E).55, .45

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
63
Participants eligible for a retraining program can be in one of four states:
A - not in the training program
B - discharged
C - in training
D - employed
You are given the following transition matrix and the fundamental matrix.
Assume that there were initially 10 people not in the training program (State A) and 60 people who were in the training program (State C). Approximately how many people will end up being discharged?
A) 10
B) 15
C) 40
D) 55
E) 60
A - not in the training program
B - discharged
C - in training
D - employed
You are given the following transition matrix and the fundamental matrix.
Assume that there were initially 10 people not in the training program (State A) and 60 people who were in the training program (State C). Approximately how many people will end up being discharged?
A) 10
B) 15
C) 40
D) 55
E) 60

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
64
The transition matrix below shows the probabilities that customer switch between two grocery stores, Don's and Limmer's, each week. If there are 2000 customers who shop at either store, how many over the long run would shop at Limmer's?
A) 333
B) 400
C) 667
D) 1000
E) 1600
A) 333
B) 400
C) 667
D) 1000
E) 1600

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck


