Deck 2: Linear Programming: Model Formulation and Graphical Solution
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/122
Play
Full screen (f)
Deck 2: Linear Programming: Model Formulation and Graphical Solution
1
A feasible solution violates at least one of the constraints.
False
2
In linear programming models , objective functions can only be maximized.
False
3
When using the graphical method, only one of the four quadrants of an xy-axis needs to be drawn.
True
4
The equation 8xy = 32 satisfies the proportionality property of linear programming.

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
5
Proportionality means the slope of a constraint is proportional to the slope of the objective function.

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
6
Linear programming is a model consisting of linear relationships representing a firm's decisions given an objective and resource constraints.

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
7
A constraint is a linear relationship representing a restriction on decision making.

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
8
Typically, finding a corner point for the feasible region involves solving a set of three simultaneous equations.

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
9
The terms in the objective function or constraints are multiplicative.

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
10
All model parameters are assumed to be known with certainty.

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
11
The feasible solution area contains infinite solutions to the linear program.

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
12
A linear programming model consists of only decision variables and constraints.

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
13
The values of decision variables are continuous or divisible.

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
14
A parameter is a numerical value in the objective function and constraints.

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
15
Linear programming models exhibit linearity among all constraint relationships and the objective function.

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
16
All linear programming models exhibit a set of constraints.

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
17
The objective function always consists of either maximizing or minimizing some value.

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
18
The terms in the objective function or constraints are additive.

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
19
The objective function is a linear relationship reflecting the objective of an operation.

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
20
Objective functions in linear programs always minimize costs.

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
21
A minimization model of a linear program contains only surplus variables.

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
22
A ________ is a linear relationship representing a restriction on decision making.

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
23
If at least one constraint in a linear programming model is violated, the solution is said to be ________.

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
24
There is exactly one optimal solution point to a linear program.

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
25
In the graphical approach, simultaneous equations may be used to solve for the optimal solution point.

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
26
The following equation represents a resource constraint for a maximization problem: X + Y ≥ 20.

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
27
A graphical solution is limited to solving linear programming problems with ________ decision variables

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
28
The optimal solution for a graphical linear programming problem is the corner point that is the farthest from the origin.

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
29
Multiple optimal solutions can occur when the objective function line is ________ to a constraint line.

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
30
If the objective function is parallel to a constraint, the constraint is infeasible.

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
31
Multiple optimal solutions occur when constraints are parallel to each other.

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
32
The first step in formulating a linear programming model is to define the objective function

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
33
Surplus variables are only associated with minimization problems.

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
34
Slack variables are only associated with maximization problems.

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
35
A manufacturer using linear programming to decide the best product mix to maximize profit typically has a(n) ________ constraint included in the model.

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
36
The ________ solution area is an area bounded by the constraint equations.

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
37
When a maximization problem is ________, the objective function can increase indefinitely without reaching a maximum value.

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
38
The ________ is a linear relationship reflecting the objective of an operation.

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
39
Graphical solutions to linear programming problems have an infinite number of possible objective function lines.

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
40
________ are mathematical symbols representing levels of activity.

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
41
Solve the following graphically:
Max z = 3x1 + 4x2
s.t. x1 + 2x2 ?16
2x1 + 3x2 ? 18
x1 ? 2
x2 ? 10
x1, x2 ? 0
What are the optimal values of x1, x2, and z?
Max z = 3x1 + 4x2
s.t. x1 + 2x2 ?16
2x1 + 3x2 ? 18
x1 ? 2
x2 ? 10
x1, x2 ? 0
What are the optimal values of x1, x2, and z?

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
42
Consider the following linear program:
MIN Z = 60A + 50B
s.t. 10A + 20B ? 200
8A + 5B ? 80
A ? 2
B ? 5
Solve this linear program graphically and determine the optimal quantities of A, B, and the value of Z.
MIN Z = 60A + 50B
s.t. 10A + 20B ? 200
8A + 5B ? 80
A ? 2
B ? 5
Solve this linear program graphically and determine the optimal quantities of A, B, and the value of Z.

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
43
The constraint 2X +XY violates the ________ property of linear programming.

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
44
If the objective function is parallel to a constraint, the linear program could have ________.

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
45
The management scientist constructed a linear program to help the alchemist maximize his gold production process. The computer model chugged away for a few minutes and returned an answer of infinite profit., which is what might be expected from a(n) ________ problem.

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
46
In a constraint, the ________ variable represents unused resources.

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
47
________ are at the endpoints of the constraint line segment that the objective function parallels.

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
48
Consider the following minimization problem:
Min z = x1 + 2x2
s.t. x1 + x2 ? 300
2x1 + x2 ? 400
2x1 + 5x2 ? 750
x1, x2 ? 0
Which constraints are binding at the optimal solution? (x1 =250, x2 = 50)
Min z = x1 + 2x2
s.t. x1 + x2 ? 300
2x1 + x2 ? 400
2x1 + 5x2 ? 750
x1, x2 ? 0
Which constraints are binding at the optimal solution? (x1 =250, x2 = 50)

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
49
A graphical representation of a linear program is shown below. The shaded area represents the feasible region, and the dashed line in the middle is the slope of the objective function. 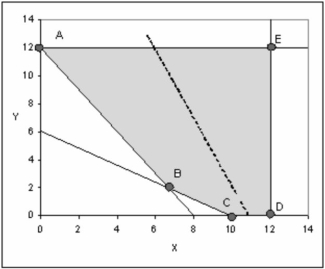
If this is a maximization, which extreme point is the optimal solution?

If this is a maximization, which extreme point is the optimal solution?

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
50
________ is the difference between the left- and right-hand sides of a greater than or equal to constraint.

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
51
The best feasible solution is ________.

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
52
Corner points on the boundary of the feasible solution area are called ________ points.

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
53
A linear programming problem that results in a solution that is ________ usually indicates that the linear program has been incorrectly formulated.

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
54
Consider the following linear program:
MAX Z = 60A + 50B
s.t. 10A + 20B ? 200
8A + 5B ? 80
A ? 2
B ? 5
Solve this linear program graphically and determine the optimal quantities of A, B, and the value of Z.
MAX Z = 60A + 50B
s.t. 10A + 20B ? 200
8A + 5B ? 80
A ? 2
B ? 5
Solve this linear program graphically and determine the optimal quantities of A, B, and the value of Z.

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
55
Consider the following minimization problem:
Min z = x1 + 2x2
s.t. x1 + x2 ? 300
2x1 + x2 ? 400
2x1 + 5x2 ? 750
x1, x2 ? 0
What is the optimal solution?
Min z = x1 + 2x2
s.t. x1 + x2 ? 300
2x1 + x2 ? 400
2x1 + 5x2 ? 750
x1, x2 ? 0
What is the optimal solution?

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
56
The ________ property of linear programming models indicates that the values of all the model parameters are known and are assumed to be constant.

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
57
The ________ step in formulating a linear programming model is to define the decision variables.

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
58
The ________ property of linear programming models indicates that the rate of change, or slope, of the objective function or a constraint is constant.

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
59
The ________ property of linear programming models indicates that the decision variables cannot be restricted to integer values and can take on any fractional value.

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
60
A graphical representation of a linear program is shown below. The shaded area represents the feasible region, and the dashed line in the middle is the slope of the objective function. 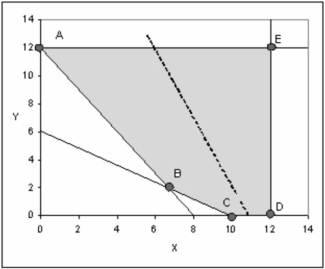
If this is a minimization, which extreme point is the optimal solution?

If this is a minimization, which extreme point is the optimal solution?

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
61
Consider the following linear programming problem:
MIN Z = 3x1 + 2x2
Subject to: 2x1 + 3x2 ? 12
5x1 + 8x2 ? 37
x1, x2 ? 0
At the optimal solution point, the objective function value is 18. If the constraints are changed from greater than to less than constraints and the objective function is changed from minimize to maximize, what happens to the optimal solution? Demonstrate whether it falls at the same optimal point.
MIN Z = 3x1 + 2x2
Subject to: 2x1 + 3x2 ? 12
5x1 + 8x2 ? 37
x1, x2 ? 0
At the optimal solution point, the objective function value is 18. If the constraints are changed from greater than to less than constraints and the objective function is changed from minimize to maximize, what happens to the optimal solution? Demonstrate whether it falls at the same optimal point.

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
62
A graphical representation of a linear program is shown below. The shaded area represents the feasible region, and the dashed line in the middle is the slope of the objective function. 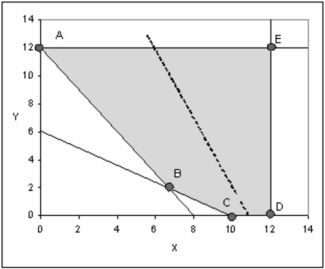
What would the be the new slope of the objective function if multiple optimal solutions occurred along line segment AB?

What would the be the new slope of the objective function if multiple optimal solutions occurred along line segment AB?

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
63
In a linear programming problem, a valid objective function can be represented as:
A) Max Z = 5xy
B) Max Z 5x2 + 2y2
C) Max 3x + 3y + 1/3 z
D) Min (x1 + x2) / x3
A) Max Z = 5xy
B) Max Z 5x2 + 2y2
C) Max 3x + 3y + 1/3 z
D) Min (x1 + x2) / x3

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
64
Consider the following linear programming problem:
MIN Z = & 2x1 + 3x2
Subject to: x1 + 2x2 ? 20
5x1 + x2 ? 40
4x1 +6x2 ? 60
x1 , x2 ? 0
What is the optimal solution?
MIN Z = & 2x1 + 3x2
Subject to: x1 + 2x2 ? 20
5x1 + x2 ? 40
4x1 +6x2 ? 60
x1 , x2 ? 0
What is the optimal solution?

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
65
The minimization of cost or maximization of profit is the
A) constraint of operations management.
B) goal of management science.
C) objective of linear programming.
D) assumption of financiality.
A) constraint of operations management.
B) goal of management science.
C) objective of linear programming.
D) assumption of financiality.

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
66
In a linear programming problem, the binding constraints for the optimal solution are:
5x1 + 3x2 ≤ 30
2x1 + 5x2 ≤ 20
Which of these objective functions will lead to the same optimal solution?
A) 2x1 + 1x2
B) 7x1 + 8x2
C) 80x1 + 60x2
D) 25x1 + 15x2
5x1 + 3x2 ≤ 30
2x1 + 5x2 ≤ 20
Which of these objective functions will lead to the same optimal solution?
A) 2x1 + 1x2
B) 7x1 + 8x2
C) 80x1 + 60x2
D) 25x1 + 15x2

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
67
A linear programming model consists of
A) decision variables.
B) an objective function.
C) constraints.
D) all of the above
A) decision variables.
B) an objective function.
C) constraints.
D) all of the above

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
68
In a linear programming problem, the binding constraints for the optimal solution are:
5x1 + 3x2 ≤ 30
2x1 + 5x2 ≤ 20
As long as the slope of the objective function stays between ________ and ________, the current optimal solution point will remain optimal.
5x1 + 3x2 ≤ 30
2x1 + 5x2 ≤ 20
As long as the slope of the objective function stays between ________ and ________, the current optimal solution point will remain optimal.

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
69
Consider the following linear programming problem:
Max Z = $15x + $20y
Subject to: 8x + 5y ? 40
0.4x + y ? 4
x, y ? 0
Determine the values for x and y that will maximize revenue. Given this optimal revenue, what is the amount of slack associated with the first constraint?
Max Z = $15x + $20y
Subject to: 8x + 5y ? 40
0.4x + y ? 4
x, y ? 0
Determine the values for x and y that will maximize revenue. Given this optimal revenue, what is the amount of slack associated with the first constraint?

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
70
Consider the following linear programming problem:
Max Z = 3x1 + 3x2
Subject to: 10x1 + 4x2 ? 60
25x1 + 50x2 ? 200
x1, x2 ? 0
Find the optimal profit and the values of x1 and x2 at the optimal solution.
Max Z = 3x1 + 3x2
Subject to: 10x1 + 4x2 ? 60
25x1 + 50x2 ? 200
x1, x2 ? 0
Find the optimal profit and the values of x1 and x2 at the optimal solution.

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
71
Given this set of constraints, for what objective function is the point x=5, y=3 in the feasible region?
s.t 3x + 6y ≤ 30
10x + 10y ≤ 60
10x + 15y ≤ 90
s.t 3x + 6y ≤ 30
10x + 10y ≤ 60
10x + 15y ≤ 90

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
72
Consider the following linear programming problem:
Max Z = $3x + $9y
Subject to: 20x + 32y ? 1600
4x + 2y ? 240
y ? 40
x, y ? 0
Solve for the quantities of x and y which will maximize Z. What is the value of the slack variable associated with constraint 2?
Max Z = $3x + $9y
Subject to: 20x + 32y ? 1600
4x + 2y ? 240
y ? 40
x, y ? 0
Solve for the quantities of x and y which will maximize Z. What is the value of the slack variable associated with constraint 2?

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
73
Consider the following linear programming problem:
MIN Z = 3x1 + 2x2
Subject to: 2x1 + 3x2 ? 12
5x1 + 8x2 ? 37
x1, x2 ? 0
What is minimum cost and the value of x1 and x2 at the optimal solution?
MIN Z = 3x1 + 2x2
Subject to: 2x1 + 3x2 ? 12
5x1 + 8x2 ? 37
x1, x2 ? 0
What is minimum cost and the value of x1 and x2 at the optimal solution?

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
74
Which of the following could not be a linear programming problem constraint?
A) 1A + 2B ≠ 3
B) 1A + 2B = 3
C) 1A + 2B ≤ 3
D) 1A + 2B ≥ 3
A) 1A + 2B ≠ 3
B) 1A + 2B = 3
C) 1A + 2B ≤ 3
D) 1A + 2B ≥ 3

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
75
Consider the following linear programming problem:
MIN Z = 10x1 + 20x2
Subject to: x1 + x2 ? 12
2x1 + 5x2 ? 40
x2 ? 13
x1, x2 ? 0
At the optimal solution, what is the value of surplus associated with constraint 1 and constraint 3, respectively?
MIN Z = 10x1 + 20x2
Subject to: x1 + x2 ? 12
2x1 + 5x2 ? 40
x2 ? 13
x1, x2 ? 0
At the optimal solution, what is the value of surplus associated with constraint 1 and constraint 3, respectively?

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
76
The poultry farmer decided to make his own chicken scratch by combining alfalfa and corn in rail car quantities. A rail car of corn costs $400 and a rail car of alfalfa costs $200. The farmer's chickens have a minimum daily requirement of vitamin K (500 milligrams) and iron (400 milligrams), but it doesn't matter whether those elements come from corn, alfalfa, or some other grain. A unit of corn contains 150 milligrams of vitamin K and 75 milligrams of iron. A unit of alfalfa contains 250 milligrams of vitamin K and 50 milligrams of iron. Formulate the linear programming model for this situation.

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
77
Consider the following linear programming problem:
MIN Z = 10x1 + 20x2
Subject to: x1 + x2 ? 12
2x1 + 5x2 ? 40
x2 ? 13
x1, x2 ? 0
What is minimum cost and the value of x1 and x2 at the optimal solution?
MIN Z = 10x1 + 20x2
Subject to: x1 + x2 ? 12
2x1 + 5x2 ? 40
x2 ? 13
x1, x2 ? 0
What is minimum cost and the value of x1 and x2 at the optimal solution?

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
78
Consider the following linear programming problem:
Max Z = 5x1 + 3x2
Subject to: 6x1 + 2x2 ? 18
15x1 + 20x2 ? 60
x1 , x2 ? 0
Find the optimal profit and the values of x1 and x2 at the optimal solution.
Max Z = 5x1 + 3x2
Subject to: 6x1 + 2x2 ? 18
15x1 + 20x2 ? 60
x1 , x2 ? 0
Find the optimal profit and the values of x1 and x2 at the optimal solution.

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
79
Decision variables
A) measure the objective function.
B) measure how much or how many items to produce, purchase, hire, etc.
C) always exist for each constraint.
D) measure the values of each constraint.
A) measure the objective function.
B) measure how much or how many items to produce, purchase, hire, etc.
C) always exist for each constraint.
D) measure the values of each constraint.

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
80
A company producing a standard line and a deluxe line of dishwashers has the following time requirements (in minutes) in departments where either model can be processed.
The standard models contribute $20 each and the deluxe $30 each to profits. Because the company produces other items that share resources used to make the dishwashers, the stamping machine is available only 30 minutes per hour, on average. The motor installation production line has 60 minutes available each hour. There are two lines for wiring, so the time availability is 90 minutes per hour.
Let x = number of standard dishwashers produced per hour
y = number of deluxe dishwashers produced per hour
Write the formulation for this linear program.
The standard models contribute $20 each and the deluxe $30 each to profits. Because the company produces other items that share resources used to make the dishwashers, the stamping machine is available only 30 minutes per hour, on average. The motor installation production line has 60 minutes available each hour. There are two lines for wiring, so the time availability is 90 minutes per hour.
Let x = number of standard dishwashers produced per hour
y = number of deluxe dishwashers produced per hour
Write the formulation for this linear program.

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck


