Deck 5: Several Useful Discrete Distributions
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/166
Play
Full screen (f)
Deck 5: Several Useful Discrete Distributions
1
Given a Poisson random variable x, where the average number of times an event occurs in a certain period of time is 2.5, what is P(x = 0)?
A) 2.5
B) 1.5811
C) 0.40
D) 0.0821
A) 2.5
B) 1.5811
C) 0.40
D) 0.0821
D
2
Which of the following experiments CANNOT be modelled by a Poisson distribution?
A) the number of calls received by a switchboard during a given period of time
B) the number of bacteria per small volume of fluid
C) the gender of individuals going through a security check at an airport in a given hour
D) the number of customer arrivals at a checkout counter during a given minute
A) the number of calls received by a switchboard during a given period of time
B) the number of bacteria per small volume of fluid
C) the gender of individuals going through a security check at an airport in a given hour
D) the number of customer arrivals at a checkout counter during a given minute
C
3
What is the standard deviation of a binomial distribution for which n = 50 and p = 0.15?
A) 50.15
B) 7.082
C) 6.375
D) 2.525
A) 50.15
B) 7.082
C) 6.375
D) 2.525
D
4
A telephone survey of Canadian families is conducted to determine the number of children in the average Canadian family. Past experience has shown that 30% of the families who are telephoned will refuse to respond to the survey. Which of the following data could NOT be classified as a binomial random variable?
A) the number of families out of 50 who respond to the survey
B) the number of families out of 50 who refuse to respond to the survey
C) the number of children in a family who respond to the survey
A) the number of families out of 50 who respond to the survey
B) the number of families out of 50 who refuse to respond to the survey
C) the number of children in a family who respond to the survey

Unlock Deck
Unlock for access to all 166 flashcards in this deck.
Unlock Deck
k this deck
5
Which of the following best describes a binominal probability distribution?
A) It is a probability distribution that shows the probabilities associated with possible values of a discrete random variable that are generated by a binomial experiment.
B) It is a probability distribution that shows, for each of a random variable's possible values, the probability of the variable being less than or equal to that value.
C) It is a probability distribution that shows the probabilities associated with possible values of a discrete random variable when the probability of success of these values changes from one trial to the next.
D) It is a probability distribution that shows the probabilities associated with possible values of a discrete random variable when these values equal the number of occurrences of a specified event within a specified time or space.
A) It is a probability distribution that shows the probabilities associated with possible values of a discrete random variable that are generated by a binomial experiment.
B) It is a probability distribution that shows, for each of a random variable's possible values, the probability of the variable being less than or equal to that value.
C) It is a probability distribution that shows the probabilities associated with possible values of a discrete random variable when the probability of success of these values changes from one trial to the next.
D) It is a probability distribution that shows the probabilities associated with possible values of a discrete random variable when these values equal the number of occurrences of a specified event within a specified time or space.

Unlock Deck
Unlock for access to all 166 flashcards in this deck.
Unlock Deck
k this deck
6
Supporters of gun control in a university town claim that 60% of the students are in favour of stronger gun control in Canada. A social scientist at the university conducts a survey of 20 randomly chosen students and finds that 9 of the 20 favour stronger gun control. Given this information, which of the following is a reasonable conclusion?
A) There is no reason to doubt the claim.
B) The survey results constitute a rare event.
C) The claim is incorrect.
D) The true percentage of students who favour stronger gun control must be 45%.
A) There is no reason to doubt the claim.
B) The survey results constitute a rare event.
C) The claim is incorrect.
D) The true percentage of students who favour stronger gun control must be 45%.

Unlock Deck
Unlock for access to all 166 flashcards in this deck.
Unlock Deck
k this deck
7
What is the expected value, E(X), of a binomial probability distribution with n trials and a probability p of success?
A) n/p
B) np(1 - p)
C) np
D) np - 1
A) n/p
B) np(1 - p)
C) np
D) np - 1

Unlock Deck
Unlock for access to all 166 flashcards in this deck.
Unlock Deck
k this deck
8
Given that n is the number of trials and p is the probability of success in any one trial of a random experiment, which of the following is equal to the expected value of a binomial random variable?
A) (n - 1)p
B) p
C) np
D) n/p
A) (n - 1)p
B) p
C) np
D) n/p

Unlock Deck
Unlock for access to all 166 flashcards in this deck.
Unlock Deck
k this deck
9
What is the expected number of heads in 200 tosses of an unbiased coin?
A) 50
B) 75
C) 100
D) 125
A) 50
B) 75
C) 100
D) 125

Unlock Deck
Unlock for access to all 166 flashcards in this deck.
Unlock Deck
k this deck
10
It has been alleged that 40% of all community college students favour Dell computers. If this were true, and we took a random sample of 25 students, the binomial probability table for cumulative values of x available in your text would reveal which of the following probabilities?
A) The probability of 10 or fewer students in favour is 0.586.
B) The probability of fewer than 19 students in favour is 1.000.
C) Both a and b.
A) The probability of 10 or fewer students in favour is 0.586.
B) The probability of fewer than 19 students in favour is 1.000.
C) Both a and b.

Unlock Deck
Unlock for access to all 166 flashcards in this deck.
Unlock Deck
k this deck
11
Which of the following scenarios is an example of a binomial experiment?
A) A shopping mall is interested in the income level of its customers and is taking a survey to gather information.
B) A business firm introducing a new product wants to know how many purchases its clients will make each year.
C) A sociologist is researching an area in an effort to determine the proportion of households with a male head of household.
D) A study is concerned with the average number of hours worked by high school students.
A) A shopping mall is interested in the income level of its customers and is taking a survey to gather information.
B) A business firm introducing a new product wants to know how many purchases its clients will make each year.
C) A sociologist is researching an area in an effort to determine the proportion of households with a male head of household.
D) A study is concerned with the average number of hours worked by high school students.

Unlock Deck
Unlock for access to all 166 flashcards in this deck.
Unlock Deck
k this deck
12
Which probability distribution is appropriate when the events of interest occur randomly, independently of one another, and rarely?
A) binomial distribution
B) Poisson distribution
C) hypergeometric distribution
D) any discrete probability distribution
A) binomial distribution
B) Poisson distribution
C) hypergeometric distribution
D) any discrete probability distribution

Unlock Deck
Unlock for access to all 166 flashcards in this deck.
Unlock Deck
k this deck
13
If the random variable x is binomially distributed with n = 10 and p = 0.05, what is P(x = 2)?
A) 0.914
B) 0.599
C) 0.55
D) 0.074
A) 0.914
B) 0.599
C) 0.55
D) 0.074

Unlock Deck
Unlock for access to all 166 flashcards in this deck.
Unlock Deck
k this deck
14
For a binomial experiment with n trials, p is the probability of success, q is the probability of failure, and x is the number of successes in n trials. Which one of the following statements is NOT a property of such an experiment?
A) p + q = 1
B) = 1 for x = 0, 1, . . ., n
C) P(x = 0) =
D) P(x = 1) =
A) p + q = 1
B) = 1 for x = 0, 1, . . ., n
C) P(x = 0) =
D) P(x = 1) =

Unlock Deck
Unlock for access to all 166 flashcards in this deck.
Unlock Deck
k this deck
15
Which of the following is NOT a characteristic of a binomial ?
A) There are n identical trials, and all trials are independent.
B) Each trial has two possible outcomes, which are traditionally labelled "failure" and "success," and the probability of success p is the same on each trial.
C) We are interested in x, the number of successes observed during the n trials.
D) The probability of failure may differ from trial to trial.
A) There are n identical trials, and all trials are independent.
B) Each trial has two possible outcomes, which are traditionally labelled "failure" and "success," and the probability of success p is the same on each trial.
C) We are interested in x, the number of successes observed during the n trials.
D) The probability of failure may differ from trial to trial.

Unlock Deck
Unlock for access to all 166 flashcards in this deck.
Unlock Deck
k this deck
16
Which of the following statements is a property of the binomial distribution?
A) The binomial distribution tends to be more symmetric as the probability of success p approaches 0.5.
B) As the number of trials increases, the expected value of the random variable decreases.
C) As the number of trials increases for a given probability of success, the binomial distribution becomes more skewed.
D) As the number of trials increases, the probability of success increases
A) The binomial distribution tends to be more symmetric as the probability of success p approaches 0.5.
B) As the number of trials increases, the expected value of the random variable decreases.
C) As the number of trials increases for a given probability of success, the binomial distribution becomes more skewed.
D) As the number of trials increases, the probability of success increases

Unlock Deck
Unlock for access to all 166 flashcards in this deck.
Unlock Deck
k this deck
17
Which of the following is NOT a characteristic of a binomial experiment?
A) The experiment consists of n identical trials.
B) The probability of failure on a single trial remains constant from trial to trial.
C) The standard deviation of the binomial random variable is independent of the number of trials.
D) Each trial results in one of two outcomes.
A) The experiment consists of n identical trials.
B) The probability of failure on a single trial remains constant from trial to trial.
C) The standard deviation of the binomial random variable is independent of the number of trials.
D) Each trial results in one of two outcomes.

Unlock Deck
Unlock for access to all 166 flashcards in this deck.
Unlock Deck
k this deck
18
A manufacturer of golf balls uses a production process that produces 10% defective balls. A quality inspector takes samples of a week's output with replacement. Using the cumulative binomial probability table available in your text, which of the following probabilities can the inspector determine?
A) If five units are inspected, the probability of at most three of these units being defective is 0.984.
B) If 10 units are inspected, the probability of 5 or 6 of these units being defective is 0.002.
C) If 15 units are inspected, the probability of at least 10 of these units being defective is 0.547.
D) If 20 units are inspected, the probability of at least 19 of these units being defective is 0.0009.
A) If five units are inspected, the probability of at most three of these units being defective is 0.984.
B) If 10 units are inspected, the probability of 5 or 6 of these units being defective is 0.002.
C) If 15 units are inspected, the probability of at least 10 of these units being defective is 0.547.
D) If 20 units are inspected, the probability of at least 19 of these units being defective is 0.0009.

Unlock Deck
Unlock for access to all 166 flashcards in this deck.
Unlock Deck
k this deck
19
What does the binomial distribution formula do?
A) It computes the number of permutations of x successes (and, therefore, n - x failures) that can be achieved in n trials of a random experiment that satisfies the conditions of the binomial experiment.
B) It computes the probability of x successes in n trials of a random experiment that satisfies the conditions of a binomial experiment.
C) It produces one of two possible outcomes, conventionally called success and failure.
D) It produces the probability of x successes when a random sample of size n is drawn without replacement from a population of size N within which M units have the characteristic that denotes success.
A) It computes the number of permutations of x successes (and, therefore, n - x failures) that can be achieved in n trials of a random experiment that satisfies the conditions of the binomial experiment.
B) It computes the probability of x successes in n trials of a random experiment that satisfies the conditions of a binomial experiment.
C) It produces one of two possible outcomes, conventionally called success and failure.
D) It produces the probability of x successes when a random sample of size n is drawn without replacement from a population of size N within which M units have the characteristic that denotes success.

Unlock Deck
Unlock for access to all 166 flashcards in this deck.
Unlock Deck
k this deck
20
A manufacturer of tennis balls uses a production process that produces 5% defective balls. A quality inspector takes samples of a week's output, with replacement. Using the cumulative binomial probability table available in your text, which of the following probabilities can the inspector determine?
A) If five units are inspected, the probability of zero units being defective is 0.774.
B) If 10 units are inspected, the probability of 2 units being defective is 0.374.
C) If 15 units are inspected, the probability of 4 units being defective is 0.999.
D) If 20 units are inspected, the probability of 6 units being defective is 0.0569.
A) If five units are inspected, the probability of zero units being defective is 0.774.
B) If 10 units are inspected, the probability of 2 units being defective is 0.374.
C) If 15 units are inspected, the probability of 4 units being defective is 0.999.
D) If 20 units are inspected, the probability of 6 units being defective is 0.0569.

Unlock Deck
Unlock for access to all 166 flashcards in this deck.
Unlock Deck
k this deck
21
In which of the following sampling methods would the hypergeometric probability distribution be used instead of the binomial distribution?
A) when sampling is performed with replacement from a finite population
B) when sampling is performed without replacement from a finite population
C) when sampling is performed without replacement from an infinite population
D) when sampling is performed with replacement from an infinite population
A) when sampling is performed with replacement from a finite population
B) when sampling is performed without replacement from a finite population
C) when sampling is performed without replacement from an infinite population
D) when sampling is performed with replacement from an infinite population

Unlock Deck
Unlock for access to all 166 flashcards in this deck.
Unlock Deck
k this deck
22
If the standard deviation for a Poisson random variable is known to be 3.60, what is its expected value?
A) approximately 1.90
B) 3.60
C) 8.28
D) 12.96
A) approximately 1.90
B) 3.60
C) 8.28
D) 12.96

Unlock Deck
Unlock for access to all 166 flashcards in this deck.
Unlock Deck
k this deck
23
Suppose we are given that n is the number of trials of a random experiment, N is population size, M is the number of population units with the "success" characteristic, and p is the probability of success in the first trial. Under those circumstances, which of these expressions equals the mean of the hypergeometric random variable's probability distribution?
A) n
B) np
C) n(N/M)
D) n(M/N)
A) n
B) np
C) n(N/M)
D) n(M/N)

Unlock Deck
Unlock for access to all 166 flashcards in this deck.
Unlock Deck
k this deck
24
Which of the following best describes a Poisson random variable?
A) It is a continuous random variable with infinitely many possible values.
B) It is a discrete random variable with infinitely many possible values.
C) It is a continuous random variable with a finite number of possible values.
D) It is a discrete random variable with a finite number of possible values.
A) It is a continuous random variable with infinitely many possible values.
B) It is a discrete random variable with infinitely many possible values.
C) It is a continuous random variable with a finite number of possible values.
D) It is a discrete random variable with a finite number of possible values.

Unlock Deck
Unlock for access to all 166 flashcards in this deck.
Unlock Deck
k this deck
25
Which of the following distributions could NOT be used to describe the exact distribution for a discrete random variable?
A) binomial distribution
B) Poisson distribution
C) hypergeometric distribution
D) normal distribution
A) binomial distribution
B) Poisson distribution
C) hypergeometric distribution
D) normal distribution

Unlock Deck
Unlock for access to all 166 flashcards in this deck.
Unlock Deck
k this deck
26
A coin-toss experiment represents a binomial experiment only if the coin is balanced, meaning that p = 0.5.

Unlock Deck
Unlock for access to all 166 flashcards in this deck.
Unlock Deck
k this deck
27
Which of the following correctly describes a Poisson random variable?
A) It does not generate a binomial either/or outcome because only a single type of outcome or "event" is occurring during the Poisson process.
B) It equals the number of occurrences of a specified event within a specified time or space.
C) a and b
A) It does not generate a binomial either/or outcome because only a single type of outcome or "event" is occurring during the Poisson process.
B) It equals the number of occurrences of a specified event within a specified time or space.
C) a and b

Unlock Deck
Unlock for access to all 166 flashcards in this deck.
Unlock Deck
k this deck
28
A binomial random variable is an example of a discrete random variable.

Unlock Deck
Unlock for access to all 166 flashcards in this deck.
Unlock Deck
k this deck
29
What kinds of probabilities does the hypergeometric probability distribution provide?
A) It provides probabilities associated with possible values of a binomial random variable in situations in which sampling is done without replacement.
B) It provides probabilities associated with possible values of a binomial random variable in situations in which the probability of success changes from one trial to the next.
C) both a and b
D) neither a or b
A) It provides probabilities associated with possible values of a binomial random variable in situations in which sampling is done without replacement.
B) It provides probabilities associated with possible values of a binomial random variable in situations in which the probability of success changes from one trial to the next.
C) both a and b
D) neither a or b

Unlock Deck
Unlock for access to all 166 flashcards in this deck.
Unlock Deck
k this deck
30
Which of these statements is NOT a property of a Poisson distribution?
A) The Poisson distribution is an example of a discrete probability distribution.
B) The Poisson distribution is more skewed to the right for smaller values of the parameter.
C) The Poisson distribution is symmetrical when the value of the parameteris close to 5.
D) The mean of the Poisson distribution variable is equal to the variance.
A) The Poisson distribution is an example of a discrete probability distribution.
B) The Poisson distribution is more skewed to the right for smaller values of the parameter.
C) The Poisson distribution is symmetrical when the value of the parameteris close to 5.
D) The mean of the Poisson distribution variable is equal to the variance.

Unlock Deck
Unlock for access to all 166 flashcards in this deck.
Unlock Deck
k this deck
31
A small community college in Ontario has four student organizations (A, B, C, and D). Organization A has 5 students, B has 8, C has 10, and D has 12. It is thought that new students have no preference for one of these organizations over the other. If seven new students are admitted to the college, what is the probability that one student will choose organization A, one will choose B, two will choose C, and three will choose D?
A) approximately 0.059
B) 0.200
C) approximately 0.243
D) 0.258
A) approximately 0.059
B) 0.200
C) approximately 0.243
D) 0.258

Unlock Deck
Unlock for access to all 166 flashcards in this deck.
Unlock Deck
k this deck
32
In a binomial experiment, the probability of success is the same on every trial.

Unlock Deck
Unlock for access to all 166 flashcards in this deck.
Unlock Deck
k this deck
33
Which of the following CANNOT generate a Poisson distribution?
A) the number of telephone calls received by a switchboard in a specified time period
B) the number of customers arriving at a gas station on Christmas day
C) the number of bacteria found in a cubic yard of soil
D) the number of children in a family
A) the number of telephone calls received by a switchboard in a specified time period
B) the number of customers arriving at a gas station on Christmas day
C) the number of bacteria found in a cubic yard of soil
D) the number of children in a family

Unlock Deck
Unlock for access to all 166 flashcards in this deck.
Unlock Deck
k this deck
34
The number of traffic accidents per day on a certain section of highway is thought to be Poisson distributed with a mean to equal 2.19. Which of the following best approximates the probability of no accidents occurring on this section of highway during a one-day period?
A) 0.457
B) 0.318
C) 0.296
D) 0.112
A) 0.457
B) 0.318
C) 0.296
D) 0.112

Unlock Deck
Unlock for access to all 166 flashcards in this deck.
Unlock Deck
k this deck
35
The number of traffic accidents per day on a certain section of highway is thought to be distributed with a mean equal to 2.19. What is the standard deviation of the number of accidents?
A) approximately 4.80
B) 3.14
C) 2.19
D) approximately 1.48
A) approximately 4.80
B) 3.14
C) 2.19
D) approximately 1.48

Unlock Deck
Unlock for access to all 166 flashcards in this deck.
Unlock Deck
k this deck
36
In a book, two misprints occur per 100 pages. Using the cumulative Poisson probability table available in your text, which of the following probabilities can we determine for a book of 500 pages?
A) The probability of finding 5 or 6 misprints equals 0.099.
B) The probability of finding at least 20 misprints equals 0.003.
C) The probability of finding at least 24 misprints equals 0.1234.
A) The probability of finding 5 or 6 misprints equals 0.099.
B) The probability of finding at least 20 misprints equals 0.003.
C) The probability of finding at least 24 misprints equals 0.1234.

Unlock Deck
Unlock for access to all 166 flashcards in this deck.
Unlock Deck
k this deck
37
Which of the following best describes our options when evaluating probabilities if we use the hypergeometric formula 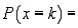
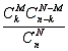 ?
?
A) We may calculate the probability of k successes when a random sample of size n is drawn without replacement from a population of size N within which M units have the characteristic that denotes success.
B) We may assume that n < N and M < N.
C) both a and b
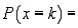
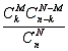 ?
?A) We may calculate the probability of k successes when a random sample of size n is drawn without replacement from a population of size N within which M units have the characteristic that denotes success.
B) We may assume that n < N and M < N.
C) both a and b

Unlock Deck
Unlock for access to all 166 flashcards in this deck.
Unlock Deck
k this deck
38
The number of traffic accidents per day on a certain section of highway is thought to be Poisson distributed with a mean equal to 2.19. Based on this, how many traffic accidents should be expected during a period of one week?
A) 15.33
B) approximately 12.21
C) 10.95
D) approximately 10.36
A) 15.33
B) approximately 12.21
C) 10.95
D) approximately 10.36

Unlock Deck
Unlock for access to all 166 flashcards in this deck.
Unlock Deck
k this deck
39
Given a Poisson random variable x, where the average number of times an event occurs in a certain period of time or space is 1.5, then what is P(x = 2)?
A) 0.5020
B) 0.2510
C) 0.2231
D) 0.01116
A) 0.5020
B) 0.2510
C) 0.2231
D) 0.01116

Unlock Deck
Unlock for access to all 166 flashcards in this deck.
Unlock Deck
k this deck
40
When sampling without replacement, which of the following is the appropriate probability distribution to use?
A) the binomial distribution
B) the hypergeometric distribution
C) the Poisson distribution
D) the normal approximation to the binomial distribution
A) the binomial distribution
B) the hypergeometric distribution
C) the Poisson distribution
D) the normal approximation to the binomial distribution

Unlock Deck
Unlock for access to all 166 flashcards in this deck.
Unlock Deck
k this deck
41
The Poisson probability distribution is an example of a continuous probability distribution.

Unlock Deck
Unlock for access to all 166 flashcards in this deck.
Unlock Deck
k this deck
42
A jug contains five black marbles and five white marbles well mixed. A marble is removed and its colour is noted. A second marble is removed, without replacing the first marble, and its colour is also noted. If x is the total number of black marbles in the two draws, then x has a binomial distribution.

Unlock Deck
Unlock for access to all 166 flashcards in this deck.
Unlock Deck
k this deck
43
The probability distribution of a Poisson random variable provides a good model for data that represent the number of occurrences of a specified event in a given unit of time or space.

Unlock Deck
Unlock for access to all 166 flashcards in this deck.
Unlock Deck
k this deck
44
If x is a binomial random variable with n = 20, and p = 0.5, then P(x = 20) = 1.0.

Unlock Deck
Unlock for access to all 166 flashcards in this deck.
Unlock Deck
k this deck
45
The binomial probability distribution could be used to describe the speed of tennis balls when the players are serving.

Unlock Deck
Unlock for access to all 166 flashcards in this deck.
Unlock Deck
k this deck
46
A binomial experiment is a sequence of n identical trials such that both of the following properties hold:
a.) each trial produces one of two outcomes that are conventionally called "success" and "failure," and
b.) each trial is independent of any other trial so that the probability of success or failure is constant from trial to trial.
a.) each trial produces one of two outcomes that are conventionally called "success" and "failure," and
b.) each trial is independent of any other trial so that the probability of success or failure is constant from trial to trial.

Unlock Deck
Unlock for access to all 166 flashcards in this deck.
Unlock Deck
k this deck
47
A binomial probability distribution shows the probabilities associated with possible values of a discrete random variable that are generated by a binomial experiment.

Unlock Deck
Unlock for access to all 166 flashcards in this deck.
Unlock Deck
k this deck
48
Where n = 100 is the number of trials and p = 0.04 is the probability of success in each trial, the mean of a binomial experiment is 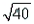 .
.
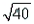 .
.
Unlock Deck
Unlock for access to all 166 flashcards in this deck.
Unlock Deck
k this deck
49
Where n = 150 is the number of trials and p = 0.6 is the probability of success in each trial, the standard deviation of a binomial experiment is 36.

Unlock Deck
Unlock for access to all 166 flashcards in this deck.
Unlock Deck
k this deck
50
A binomial experiment requires that the success and failure probabilities be constant from one trial to the next, and also that these two probabilities be equal to each other.

Unlock Deck
Unlock for access to all 166 flashcards in this deck.
Unlock Deck
k this deck
51
The number of defects in a random sample of 200 parts produced by a machine is binomially distributed with p = 0.03. Based on this information, the standard deviation of the number of defects in the sample is 5.82.

Unlock Deck
Unlock for access to all 166 flashcards in this deck.
Unlock Deck
k this deck
52
The distribution of the number of phone calls to a doctor's office in a one-hour time period is likely to be described by a binomial distribution.

Unlock Deck
Unlock for access to all 166 flashcards in this deck.
Unlock Deck
k this deck
53
As a rule of thumb, if the sample size n is large relative to the population size N, in particular, if n/N > 0.05, then the resulting experiment will NOT be binomial.

Unlock Deck
Unlock for access to all 166 flashcards in this deck.
Unlock Deck
k this deck
54
The number of defects in a random sample of 200 parts produced by a machine is binomially distributed with p = 0.03. Based on this information, the expected number of defects in the sample is six.

Unlock Deck
Unlock for access to all 166 flashcards in this deck.
Unlock Deck
k this deck
55
The number of successes observed during the n trials of a binomial experiment is called the binomial random variable.

Unlock Deck
Unlock for access to all 166 flashcards in this deck.
Unlock Deck
k this deck
56
A life insurance salesperson makes 15 sales calls daily. The chance of making a sale on each call is 0.40. The probability that he will make at most two sales is less than 0.10.

Unlock Deck
Unlock for access to all 166 flashcards in this deck.
Unlock Deck
k this deck
57
The Poisson probability distribution provides a good approximation to binomial probabilities when n is large and 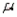 = np is small, preferably with np < 7.
= np is small, preferably with np < 7.
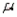 = np is small, preferably with np < 7.
= np is small, preferably with np < 7.
Unlock Deck
Unlock for access to all 166 flashcards in this deck.
Unlock Deck
k this deck
58
The binomial distribution is used to describe continuous random variables.

Unlock Deck
Unlock for access to all 166 flashcards in this deck.
Unlock Deck
k this deck
59
There are only two possible outcomes in a binomial experiment where n is the number of trials and p is the probability of success in each trial.

Unlock Deck
Unlock for access to all 166 flashcards in this deck.
Unlock Deck
k this deck
60
The binomial random variable is the number of successes that occur in a certain period of time or space.

Unlock Deck
Unlock for access to all 166 flashcards in this deck.
Unlock Deck
k this deck
61
From past experience, it is known 90% of one-year-old children can distinguish their mother's voice from the voice of a similar-sounding female. A random sample of 20 one-year-olds are given this voice recognition test.
a. Find the probability that at least three children do not recognize their mother's voice.
b. Find the probability that all 20 children recognize their mother's voice.
c. Let the random variable x denote the number of children who do not recognize their mother's voice. Find the mean of x.
d. Let the random variable x denote the number of children who do not recognize their mother's voice. Find the variance of x.
e. Find the probability that, at most, four children do not recognize their mother's voice.
a. Find the probability that at least three children do not recognize their mother's voice.
b. Find the probability that all 20 children recognize their mother's voice.
c. Let the random variable x denote the number of children who do not recognize their mother's voice. Find the mean of x.
d. Let the random variable x denote the number of children who do not recognize their mother's voice. Find the variance of x.
e. Find the probability that, at most, four children do not recognize their mother's voice.

Unlock Deck
Unlock for access to all 166 flashcards in this deck.
Unlock Deck
k this deck
62
A warehouse contains six parts made by company A and ten parts made by company B. If four parts are selected at random from the warehouse, the probability that none of the four parts is from company A is approximately 0.1154.

Unlock Deck
Unlock for access to all 166 flashcards in this deck.
Unlock Deck
k this deck
63
A fellow student tells you he is working with a discrete random variable, x, which takes on integer values from 0 to 50 and has a mean of 40 and a variance of 10. Is x a binomial random variable?

Unlock Deck
Unlock for access to all 166 flashcards in this deck.
Unlock Deck
k this deck
64
The Poisson probability tables list the probabilities of x occurrences in a Poisson process for various values of 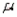 , the mean number of occurrences.
, the mean number of occurrences.
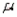 , the mean number of occurrences.
, the mean number of occurrences.
Unlock Deck
Unlock for access to all 166 flashcards in this deck.
Unlock Deck
k this deck
65
The taste test for PTC (phenylthiourea) is a common class demonstration in the study of genetics. It is known that 70% of Canadians are "tasters" and 30% are "non-tasters." Suppose a genetics class of size 20 does the test to see if they match the Canadian percentage of "tasters" and "non-tasters." (Assume the assignment of students to classes constitutes a random process.)
a. What is the probability distribution of the random variable x, the number of "non-tasters" in the class?
b. Find P(3 < x < 9).
c. Find the mean of x.
d. Find the variance of x.
a. What is the probability distribution of the random variable x, the number of "non-tasters" in the class?
b. Find P(3 < x < 9).
c. Find the mean of x.
d. Find the variance of x.

Unlock Deck
Unlock for access to all 166 flashcards in this deck.
Unlock Deck
k this deck
66
A quiz consists of 15 multiple-choice questions. Each question has five choices, with exactly one correct choice. A student, totally unprepared for the quiz, guesses on each of the 15 questions.
a. How many questions should the student expect to answer correctly?
b. What is the standard deviation of the number of questions answered correctly?
c. If at least nine questions must be answered correctly to pass the quiz, what is the chance the student passes?
a. How many questions should the student expect to answer correctly?
b. What is the standard deviation of the number of questions answered correctly?
c. If at least nine questions must be answered correctly to pass the quiz, what is the chance the student passes?

Unlock Deck
Unlock for access to all 166 flashcards in this deck.
Unlock Deck
k this deck
67
Suppose 40% of the TV sets in use in Canada on a particular night were tuned into game 7 of the Stanley Cup Playoffs.
a. If we were to take a sample of six in-use TV sets that night, what is the probability exactly three are tuned to the Stanley Cup Playoffs?
b. If, instead, the sample consisted of 15 in-use TVs, what is the probability 5 or more are tuned to the Stanley Cup Playoffs?
a. If we were to take a sample of six in-use TV sets that night, what is the probability exactly three are tuned to the Stanley Cup Playoffs?
b. If, instead, the sample consisted of 15 in-use TVs, what is the probability 5 or more are tuned to the Stanley Cup Playoffs?

Unlock Deck
Unlock for access to all 166 flashcards in this deck.
Unlock Deck
k this deck
68
The Poisson distribution is appropriate to determine the probability of a given number of defective items in a shipment.

Unlock Deck
Unlock for access to all 166 flashcards in this deck.
Unlock Deck
k this deck
69
The Poisson parameter 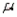 is the mean number of occurrences of an event per unit of time or space during the Poisson process.
is the mean number of occurrences of an event per unit of time or space during the Poisson process.
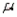 is the mean number of occurrences of an event per unit of time or space during the Poisson process.
is the mean number of occurrences of an event per unit of time or space during the Poisson process.
Unlock Deck
Unlock for access to all 166 flashcards in this deck.
Unlock Deck
k this deck
70
Hypergeometric probability distributions are examples of discrete probability distributions.

Unlock Deck
Unlock for access to all 166 flashcards in this deck.
Unlock Deck
k this deck
71
A hypergeometric probability distribution shows the probabilities associated with possible values of a discrete random variable when these values are generated by sampling with replacement, and the probability of success, therefore, changes from one trial to the next.

Unlock Deck
Unlock for access to all 166 flashcards in this deck.
Unlock Deck
k this deck
72
A warehouse contains six parts made by company A and ten parts made by company B. If four parts are selected at random from the warehouse, the probability that all four parts are from company B is approximately 0.008.

Unlock Deck
Unlock for access to all 166 flashcards in this deck.
Unlock Deck
k this deck
73
A Poisson process is the occurrence of a series of events of a given type in a random pattern over time or space such that (1) the number of occurrences within a specified time or space can equal any integer between zero and infinity, (2) the number of occurrences within one unit of time or space is independent of that in any other such (nonoverlapping) unit, and (3) the probability of occurrences is the same in all such units.

Unlock Deck
Unlock for access to all 166 flashcards in this deck.
Unlock Deck
k this deck
74
The mean of a Poisson distribution variable, where 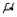 is the average number of successes occurring in a specified interval, is
is the average number of successes occurring in a specified interval, is 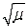 .
.
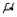 is the average number of successes occurring in a specified interval, is
is the average number of successes occurring in a specified interval, is 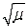 .
.
Unlock Deck
Unlock for access to all 166 flashcards in this deck.
Unlock Deck
k this deck
75
An oil firm plans to drill 20 wells, each having a probability 0.2 of striking oil. Each well costs $20,000 to drill; a well that strikes oil will bring in $750,000 in revenue. Find the expected gain from the 20 wells.

Unlock Deck
Unlock for access to all 166 flashcards in this deck.
Unlock Deck
k this deck
76
The Poisson random variable is the number of successes achieved when a random sample of size n is drawn without replacement from a population of size N within which M units have the characteristic that denotes success.

Unlock Deck
Unlock for access to all 166 flashcards in this deck.
Unlock Deck
k this deck
77
The hypergeometric probability distribution formula calculates the probability of x successes when a random sample of size n is drawn without replacement from a population of size N within which M units have the characteristic that denotes success, and N - M units have the characteristic that denotes failure.

Unlock Deck
Unlock for access to all 166 flashcards in this deck.
Unlock Deck
k this deck
78
Hypergeometric probability distributions are examples of continuous probability distributions.

Unlock Deck
Unlock for access to all 166 flashcards in this deck.
Unlock Deck
k this deck
79
A warehouse contains six parts made by company A and ten parts made by company B. If four parts are selected at random from the warehouse, the probability that one of the four parts is from company B is approximately 0.1099.

Unlock Deck
Unlock for access to all 166 flashcards in this deck.
Unlock Deck
k this deck
80
The mean and variance of a Poisson distribution variable are equal.

Unlock Deck
Unlock for access to all 166 flashcards in this deck.
Unlock Deck
k this deck


