Deck 4: A: probability and Probability Distributions
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/107
Play
Full screen (f)
Deck 4: A: probability and Probability Distributions
1
Which of the following may be used to represent the sample space of an experiment?
A) a joint probability table
B) the additive rule of probability
C) the multiplicative rule of probability
D) a tree diagram
A) a joint probability table
B) the additive rule of probability
C) the multiplicative rule of probability
D) a tree diagram
D
2
What is any subset of the sample space called?
A) an event
B) an experiment
C) a mutually exclusive event
D) independent events
A) an event
B) an experiment
C) a mutually exclusive event
D) independent events
A
3
Which of the following is a useful graphical method for displaying the sample space of an experiment?
A) a tree diagram
B) a box plot
C) a histogram
D) a scatterplot
A) a tree diagram
B) a box plot
C) a histogram
D) a scatterplot
A
4
Suppose P(A) = 0.4, P(B) = 0.3, and P(A  B) = 0. Which one of the following statements correctly defines the relationship between events A and B?
B) = 0. Which one of the following statements correctly defines the relationship between events A and B?
A) Events A and B are independent, but not mutually exclusive.
B) Events A and B are mutually exclusive, but not independent.
C) Events A and B are neither mutually exclusive nor independent.
D) Events A and B are both mutually exclusive and independent.
 B) = 0. Which one of the following statements correctly defines the relationship between events A and B?
B) = 0. Which one of the following statements correctly defines the relationship between events A and B?A) Events A and B are independent, but not mutually exclusive.
B) Events A and B are mutually exclusive, but not independent.
C) Events A and B are neither mutually exclusive nor independent.
D) Events A and B are both mutually exclusive and independent.

Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
5
What is the set of all simple events of an experiment called?
A) a compound event
B) a sample space
C) a population
D) a random sample
A) a compound event
B) a sample space
C) a population
D) a random sample

Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
6
If P(A/B) = P(A), or P(B/A) = P(B), which of the following best describes the events A and B?
A) They are mutually exclusive.
B) They are disjoint.
C) They are independent.
D) They are dependent.
A) They are mutually exclusive.
B) They are disjoint.
C) They are independent.
D) They are dependent.

Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
7
If P(A) = 0.42 and P(B) = 0.38, then what is P(A  B)?
B)?
A) 0.80
B) 0.58
C) 0.04
D) cannot be determined from the information given
 B)?
B)?A) 0.80
B) 0.58
C) 0.04
D) cannot be determined from the information given

Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
8
When Cynthia enters a grocery store, there are three simple events: buy nothing, buy a small amount, or buy a large amount. In this situation, if Cynthia buys a small amount, she cannot also buy a large amount or buy nothing. How may one best classify these three events?
A) They are mutually exclusive events.
B) They are not mutually exclusive events.
C) They are dependent events.
D) They are independent events.
A) They are mutually exclusive events.
B) They are not mutually exclusive events.
C) They are dependent events.
D) They are independent events.

Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
9
If P(A) = 0.40, P(B) = 0.30, and P(A  B) = 0.12, then what could you deduce about the events A and B?
B) = 0.12, then what could you deduce about the events A and B?
A) They are dependent events.
B) They are independent events.
C) They are mutually exclusive events.
D) They are disjoint events.
 B) = 0.12, then what could you deduce about the events A and B?
B) = 0.12, then what could you deduce about the events A and B?A) They are dependent events.
B) They are independent events.
C) They are mutually exclusive events.
D) They are disjoint events.

Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
10
Which of the following best describes all the outcomes (simple events) contained in one or the other of two random events, or possibly in both?
A) the events of an experiment
B) the intersection of two events
C) the probability space of an experiment
D) the union of two events
A) the events of an experiment
B) the intersection of two events
C) the probability space of an experiment
D) the union of two events

Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
11
If P(A) = 0.30, P(B) = 0.40, and P(A  B) = 0.20, what is the value of P(A/B)?
B) = 0.20, what is the value of P(A/B)?
A) 0.08
B) 0.12
C) 0.50
D) 0.67
 B) = 0.20, what is the value of P(A/B)?
B) = 0.20, what is the value of P(A/B)?A) 0.08
B) 0.12
C) 0.50
D) 0.67

Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
12
If events A and B are mutually exclusive, then what is the probability of both events occurring simultaneously?
A) -1
B) 0
C) 1
D) any value between 0 and 1
A) -1
B) 0
C) 1
D) any value between 0 and 1

Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
13
Suppose that an experiment consists of tossing three unbiased coins simultaneously. How many simple events are contained in this experiment?
A) 3
B) 6
C) 8
D) 9
A) 3
B) 6
C) 8
D) 9

Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
14
What does the notation 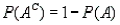 represent?
represent?
A) the union of two events
B) the intersection of two events
C) the complement of an event
D) the additive rule of probability
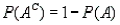 represent?
represent?A) the union of two events
B) the intersection of two events
C) the complement of an event
D) the additive rule of probability

Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
15
Suppose you are told that an experiment consists of three stages and that there are three ways to accomplish the first stage, four ways to accomplish the second stage, and five to accomplish the third stage. What would be the number of ways to accomplish the experiment?
A) 12
B) 15
C) 20
D) 60
A) 12
B) 15
C) 20
D) 60

Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
16
Which of the following is the best description of an event?
A) an experiment that is not controlled by the decision maker
B) the list of all possible simple events of an experiment
C) a collection of one or more simple events
D) a collection of two or more simple events
A) an experiment that is not controlled by the decision maker
B) the list of all possible simple events of an experiment
C) a collection of one or more simple events
D) a collection of two or more simple events

Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
17
How many ways can one choose a combination of three items out of eight distinct items?
A) 28
B) 56
C) 112
D) 224
A) 28
B) 56
C) 112
D) 224

Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
18
If P(A) = 0.80, P(B) = 0.70, and P(A 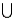 B) = 0.90, then what is the value of P(A
B) = 0.90, then what is the value of P(A  B)?
B)?
A) 0.56
B) 0.60
C) 0.63
D) 0.72
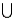 B) = 0.90, then what is the value of P(A
B) = 0.90, then what is the value of P(A  B)?
B)?A) 0.56
B) 0.60
C) 0.63
D) 0.72

Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
19
Which of the following correctly describes experiments?
A) They are two random events, A and B, such that the probability of one event is not affected by the occurrence of the other event; therefore, P(A) = P(A|B).
B) They are different events that have no outcomes in common.
C) They are activities that result in one and only one of several clearly defined possible outcomes and from which one may not predict, in advance, which of these outcomes will prevail in any particular instance.
D) They are different events that have different outcomes.
A) They are two random events, A and B, such that the probability of one event is not affected by the occurrence of the other event; therefore, P(A) = P(A|B).
B) They are different events that have no outcomes in common.
C) They are activities that result in one and only one of several clearly defined possible outcomes and from which one may not predict, in advance, which of these outcomes will prevail in any particular instance.
D) They are different events that have different outcomes.

Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
20
What is the sum of the probability of an event and the probability of its complement?
A) -1
B) 0
C) 1
D) any value between 0 and 1
A) -1
B) 0
C) 1
D) any value between 0 and 1

Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
21
Which of the following is a (are) required condition(s) for the distribution of a discrete random variable that can assume values 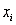 ?
?
A)
B)
C) Both (a) and (b) are required conditions.
D) The population data of the distribution must be quantitative.
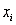 ?
?A)
B)
C) Both (a) and (b) are required conditions.
D) The population data of the distribution must be quantitative.

Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
22
The probability of an event A is equal to the sum of the probabilities of the simple events contained in A.

Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
23
Relative frequency histograms are constructed for a sample of n measurements drawn from the population, whereas the probability histogram is constructed as a model for the entire population of measurements.

Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
24
Which of the following correctly describes the nature of discrete quantitative variables?
A) They can assume values only at specific points on a scale of values, with inevitable gaps between successive observations.
B) When dealing with such variables, we can count all possible observations and, with some exceptions, that count leads to a finite result.
C) Discrete quantitative variables are correctly described by both (a) and (b).
A) They can assume values only at specific points on a scale of values, with inevitable gaps between successive observations.
B) When dealing with such variables, we can count all possible observations and, with some exceptions, that count leads to a finite result.
C) Discrete quantitative variables are correctly described by both (a) and (b).

Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
25
The probability distribution of the number of accidents in North York, Ontario, each day is given by  Which of the following could be used to describe this distribution?
Which of the following could be used to describe this distribution?
A) a continuous probability distribution
B) a discrete probability distribution
C) a conditional probability distribution
D) an expected value distribution
 Which of the following could be used to describe this distribution?
Which of the following could be used to describe this distribution?A) a continuous probability distribution
B) a discrete probability distribution
C) a conditional probability distribution
D) an expected value distribution

Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
26
In the case of independent events A, B, and C, which of the following is equal to 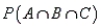 ?
?
A) P(A|B)P(B|C)P(C|A)
B) P(A|B) + P(B|C) + P(C|A)
C) P(A)P(B)P(C)
D) P(A) + P(B) + P(C)
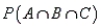 ?
?A) P(A|B)P(B|C)P(C|A)
B) P(A|B) + P(B|C) + P(C|A)
C) P(A)P(B)P(C)
D) P(A) + P(B) + P(C)

Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
27
Which of these statements is a property of the probability distribution for a discrete random variable x ?
A) The probabilities must be nonnegative.
B) The probabilities must sum to 1.
C) The random variable must take on positive values between 0 and 1.
D) Both (a) and (b) are true.
A) The probabilities must be nonnegative.
B) The probabilities must sum to 1.
C) The random variable must take on positive values between 0 and 1.
D) Both (a) and (b) are true.

Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
28
Probability is the tool that allows the statistician to use sample information to make inferences about or describe the population from which the sample was drawn.

Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
29
A false negative in screening tests (e.g., steroid testing of athletes) represents which of the following events?
A) The test is negative for a given condition, given that the person does not have the condition.
B) The test is positive for a given condition, given that the person does not have the condition.
C) The test is negative for a given condition, given that the person has the condition.
D) The test is positive for a given condition, given that the person has the condition.
A) The test is negative for a given condition, given that the person does not have the condition.
B) The test is positive for a given condition, given that the person does not have the condition.
C) The test is negative for a given condition, given that the person has the condition.
D) The test is positive for a given condition, given that the person has the condition.

Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
30
Which of the following clearly describes the general multiplicative rule of probability?
A) It is a rule of probability theory that is used to compute the probability for the occurrence of a union of two or more events: for any two events, A and B,
B) It is a rule of probability theory that is used to compute the probability for the occurrence of a union of two or more events: for any two events A and B,
C) It is a rule of probability theory that is used to compute the probability for an intersection of two or more events: for any two events, A and B,and also = P(B)P(A|B)
D) It is a rule of probability theory that is used to compute the probability for an intersection of two or more events: for any two events A and B,
A) It is a rule of probability theory that is used to compute the probability for the occurrence of a union of two or more events: for any two events, A and B,
B) It is a rule of probability theory that is used to compute the probability for the occurrence of a union of two or more events: for any two events A and B,
C) It is a rule of probability theory that is used to compute the probability for an intersection of two or more events: for any two events, A and B,and also = P(B)P(A|B)
D) It is a rule of probability theory that is used to compute the probability for an intersection of two or more events: for any two events A and B,

Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
31
A false positive in screening (e.g., home pregnancy tests) may be best described by which of the following events?
A) The test is negative for a given condition, given that the person does not have the condition.
B) The test is positive for a given condition, given that the person does not have the condition.
C) The test is negative for a given condition, given that the person has the condition.
D) The test is positive for a given condition, given that the person has the condition.
A) The test is negative for a given condition, given that the person does not have the condition.
B) The test is positive for a given condition, given that the person does not have the condition.
C) The test is negative for a given condition, given that the person has the condition.
D) The test is positive for a given condition, given that the person has the condition.

Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
32
What would be the expected number of heads turning up in 500 tosses of an unbiased coin?
A) 150
B) 200
C) 250
D) 300
A) 150
B) 200
C) 250
D) 300

Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
33
Screening tests (e.g., HIV testing) are evaluated on the probability of a false negative or a false positive. How may one classify these probabilities?
A) They are both conditional probabilities.
B) They measure the probability of the intersection of two events.
C) They measure the probability of the union of two events
D) They are both marginal probabilities.
A) They are both conditional probabilities.
B) They measure the probability of the intersection of two events.
C) They measure the probability of the union of two events
D) They are both marginal probabilities.

Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
34
Two events, A and B, are said to be dependent if and only if what condition is true?
A) P(A) = P(B).
B) P(A) increases along with P(B).
C) P(A) increases as P(B) decreases.
D) Event A is affected or changed by the occurrence of event B.
A) P(A) = P(B).
B) P(A) increases along with P(B).
C) P(A) increases as P(B) decreases.
D) Event A is affected or changed by the occurrence of event B.

Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
35
The probability distribution of the number of accidents in North York, Ontario, each day is given in the table below:  Based on this distribution, what is the approximate value of the standard deviation of the number of accidents per day?
Based on this distribution, what is the approximate value of the standard deviation of the number of accidents per day?
A) 6.95
B) 2.64
C) 2.33
D) 1.53
 Based on this distribution, what is the approximate value of the standard deviation of the number of accidents per day?
Based on this distribution, what is the approximate value of the standard deviation of the number of accidents per day?A) 6.95
B) 2.64
C) 2.33
D) 1.53

Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
36
What may NOT be said about the mean of a discrete random variable x?
A) It is denoted by.
B) It is the middle value of its probability distribution.
C) It is denoted by E(x), because it is the value of x one can expect to find, on average, by numerous repetitions of the random experiment that generates the variable's actual values.
D) It is correctly described by both (a) and (b).
A) It is denoted by.
B) It is the middle value of its probability distribution.
C) It is denoted by E(x), because it is the value of x one can expect to find, on average, by numerous repetitions of the random experiment that generates the variable's actual values.
D) It is correctly described by both (a) and (b).

Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
37
The probability distribution of the number of accidents in North York, Ontario, each day is given by  Based on this distribution, what would be the expected number of accidents on a given day?
Based on this distribution, what would be the expected number of accidents on a given day?
A) 4.62
B) 2.15
C) 1.81
D) 1.47
 Based on this distribution, what would be the expected number of accidents on a given day?
Based on this distribution, what would be the expected number of accidents on a given day?A) 4.62
B) 2.15
C) 1.81
D) 1.47

Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
38
Statistics provides ways to reason from the population to the sample, whereas probability acts in reverse, moving from the sample to the population.

Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
39
What is the term for a table, formula, or graph showing all possible values that a random variable x can assume, together with their associated probabilities p(x)?
A) a discrete probability distribution
B) a continuous probability distribution
C) a bivariate probability distribution
D) the law of total probability
A) a discrete probability distribution
B) a continuous probability distribution
C) a bivariate probability distribution
D) the law of total probability

Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
40
Which of the following best describes the concept of marginal probability?
A) It is a measure of the likelihood that a particular event will occur, regardless of whether another event occurs.
B) It is a measure of the likelihood that a particular event will occur, given the fact that another event has already occurred or is certain to occur.
C) It is a measure of the likelihood of the simultaneous occurrence of two or more events.
D) It is a direct way for defining the sample space of an experiment.
It is measure of the likelihood that either one or the other out of a possible two events will occur.
A) It is a measure of the likelihood that a particular event will occur, regardless of whether another event occurs.
B) It is a measure of the likelihood that a particular event will occur, given the fact that another event has already occurred or is certain to occur.
C) It is a measure of the likelihood of the simultaneous occurrence of two or more events.
D) It is a direct way for defining the sample space of an experiment.
It is measure of the likelihood that either one or the other out of a possible two events will occur.

Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
41
The probability of getting two heads when tossing a fair coin twice is 1/4.

Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
42
The experiment of drawing a single card once from a standard deck contains four events.

Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
43
An event is a collection of one or more simple events of an experiment.

Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
44
The probability of getting a 15 when randomly drawing a card from a well-shuffled deck is 4/52.

Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
45
Suppose that an experiment consists of tossing four unbiased coins simultaneously. The number of simple events in this experiment is 16.

Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
46
The experiment of tossing a single coin once contains one simple event.

Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
47
A tree diagram is a listing of all the simple events of an experiment.

Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
48
If an investor were interested in assessing the probability that a new supermarket will be successful in a Calgary market area, he would most likely use the relative frequency definition of probability as the method for assessing the probability of success.

Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
49
An experiment is any activity that results in one and only one of several clearly defined possible outcomes, but does not allow us to tell in advance which of these will prevail in any particular instance.

Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
50
The probability of getting the king of diamonds when randomly drawing a card from a well-shuffled deck is 1/52.

Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
51
Suppose that a patient who is complaining of several specific symptoms arrives at a doctor's office and the doctor says that she is 90% certain that the patient has the flu. In this case, it is likely that she is basing her assessment on the relative frequency approach of assigning probabilities.

Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
52
Combinations are distinguishable ordered arrangements of items, all of which have been drawn from a given group of items.

Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
53
In general, the simple events of an experiment take on values between 0 and 1.0, inclusive.

Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
54
Different events that have no outcomes in common are mutually exclusive events.

Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
55
The experiment of rolling a single die once contains six simple events.

Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
56
The sum of the probabilities for all simple events in the sample space equals 1.

Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
57
The probability of getting a black card when randomly drawing a card from a well-shuffled deck is 1/2.

Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
58
The experiment of spinning the Monte Carlo roulette wheel once contains 27 simple events.

Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
59
Invariably, Venn diagrams illustrate the intersection of two events.

Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
60
An experiment is the process by which an observation or measurement is obtained.

Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
61
The intersection of events A and B is the event that A or B or both occur.

Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
62
Two events A and B are said to be independent if P(A  B) = P(A) + P(B).
B) = P(A) + P(B).
 B) = P(A) + P(B).
B) = P(A) + P(B).
Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
63
If P(A) = 0, P(B) = 0.4, and P(A  B) = 0, then events A and B are independent.
B) = 0, then events A and B are independent.
 B) = 0, then events A and B are independent.
B) = 0, then events A and B are independent.
Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
64
If P(A) = 0.3, P(A 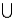 B) = 0.7, and P(A
B) = 0.7, and P(A  B) = 0.2, then P(B) = 0.2.
B) = 0.2, then P(B) = 0.2.
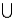 B) = 0.7, and P(A
B) = 0.7, and P(A  B) = 0.2, then P(B) = 0.2.
B) = 0.2, then P(B) = 0.2.
Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
65
The complement of an event A, denoted by 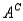 , consists of all the simple events in the sample space S that are not in A.
, consists of all the simple events in the sample space S that are not in A.
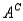 , consists of all the simple events in the sample space S that are not in A.
, consists of all the simple events in the sample space S that are not in A.
Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
66
The conditional probability of event B, given that event A has occurred is defined by 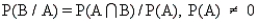 .
.
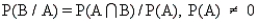 .
.
Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
67
Two events A and B are said to be independent if and only if P(A/B) = P(B) or P(B/A) = P(A).

Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
68
If P(A) > 0, P(B) > 0, and P(A  B) = 0, then the events A and B are independent.
B) = 0, then the events A and B are independent.
 B) = 0, then the events A and B are independent.
B) = 0, then the events A and B are independent.
Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
69
If P(A) = 0.4, P(B) = 0.5, and P(A  B) = 0.7, then P(A
B) = 0.7, then P(A  B) = 0.2.
B) = 0.2.
 B) = 0.7, then P(A
B) = 0.7, then P(A  B) = 0.2.
B) = 0.2.
Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
70
The probability that event A will not occur is 1 - 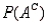 .
.
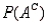 .
.
Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
71
If P(A) = 0.60, P(B) = 0.40, and P(B/A) = 0.60, then P(A/B) = 0.24.

Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
72
If P(A) > 0 and P(B) > 0, then when A and B are mutually exclusive events, they are also dependent events.

Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
73
Suppose A and B are mutually exclusive events where P(A) = 0.2 and P(B) = 0.3, then P(A 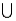 B) = 0.5.
B) = 0.5.
 B) = 0.5.
B) = 0.5.
Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
74
If P(A/B) = P(A), then events A and B are said to be independent.

Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
75
Two events A and B are said to be mutually exclusive if P(A  B) = 0.
B) = 0.
 B) = 0.
B) = 0.
Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
76
Conditional probability is the probability that an event will occur, with no other events taken into consideration.

Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
77
If P(A) = 0.4, P(B) = 0.5, and P(A  B) = 0.20, then the events A and B are mutually exclusive.
B) = 0.20, then the events A and B are mutually exclusive.
 B) = 0.20, then the events A and B are mutually exclusive.
B) = 0.20, then the events A and B are mutually exclusive.
Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
78
Suppose A and B are mutually exclusive events where P(A) = 0.1 and P(B) = 0.7, then P(A  B) = 0.8.
B) = 0.8.
 B) = 0.8.
B) = 0.8.
Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
79
If A and B are two independent events with P(A) = 0.25 and P(B) = 0.45, then P(A  B) = 0.70.
B) = 0.70.
 B) = 0.70.
B) = 0.70.
Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck
80
If A and B are independent events with P(A) = 0.30 and P(B) = 0.50, then P(A/B) is 0.15.

Unlock Deck
Unlock for access to all 107 flashcards in this deck.
Unlock Deck
k this deck


